A local hamburger shop sold a combined total of 817 hamburgers and cheeseburgers on Friday. There were 67 more cheeseburgers sold than hamburgers. How
many hamburgers were sold on Friday?
hamburgers
Answers
The number of hamburgers sold on Friday was 442.
Let us form the linear equation to find the number of burgers;
Let the cheeseburger be represented by x.
Since there were 67 more cheeseburgers sold than hamburgers. This means that hamburgers will be:
The number of hamburgers = x + 67.
Since the local hamburger shop sold a combined total of 817 hamburgers and cheeseburgers. This will be:
x + x + 67 = 817
2x + 67= 817
2x = 817 - 67
2x = 750
x = 750 / 2
x = 375
So, 375 cheeseburgers were sold on Friday.
Therefore, the number of hamburgers sold will be:
= 817 - 375
= 442
Thus, the number of hamburgers sold on Friday was 442.
To learn more about the linear equation visit:
https://brainly.com/question/13738061
#SPJ9
Related Questions
Find the point of intersection of the lines:
y = 4x + 1 and y = - 2x + 4
Answers
Answer:
(0.5, 3)
Step-by-step explanation:
i used desmos
A 30-m tall building casts a shadow. The distance from the top of the building to the tip of the shadow is 32 m. Find the length of the shadow. If necessary, round your answer to the nearest tenth.
Answers
Answer: 11.1 m
Step-by-step explanation:
This can be solved by the Pythagorean theorem where;
c² = a² + b²
c is the hypotenuse which is the distance from the top of the building to the tip of the shadow.
a is the height
c is the length
32² = 30² + b²
b² = 32² - 30²
b² = 1,024 - 900
b² = 124
b = √124
b = 11.1 m

What’s the answer for the problems 11-15 in the picture

Answers
Answer:
11.
A) EZ Pay Plan=0.15x
B) 40 to Go Plan=0.05x+40
12.
0.15x=0.05x+40
13.
x=400 minutes
14. The solution is the amount of minutes that it takes for both plans to cost the same amount. X has one solution, so it accounts for both equations.
15. EZ Pay Plan
Step-by-step explanation:
For 11, what you need to know is that the slope (coefficient of x) is the price per minute. 0.15 per minute and 0.05 per minute are charged, and therefore are the slope for those equations. The 40 on B is because it is the y intercept. No matter how long you use the object, you will always pay at least 40 dollars.
For 12, you have to find x for the minutes used.
For 13, if you do the process algebraically,
0.15x=0.05x+40
0.10x=40 (subtracted 0.05x from both sides)
x=400 (divided 0.10x and 40 by 0.10)
For 14, (no explanation)
For 15, if you substitute 200 as x, you would see that the EZ Pay Plan would make you pay 30 dollars while the 40 To Go Plan would make you pay 10+40 dollars, which 30<50.
(sorry for late response)
Is this a function?
A) yes
B) No

Answers
Answer:
Yes
Step-by-step explanation:
This is a function because every input only has one output.
let v , w ∈ r n . if ∥ v ∥ = ∥ w ∥ , show that v w and v − w are orthogonal.
Answers
If ∥v∥ = ∥w∥, then v⋅w = 0 and v⋅(v−w) = 0, showing that v⋅w and v−w are orthogonal.
How is the dot products v⋅w and v⋅(v−w) related to the orthogonality of v−w and v⋅w when ∥v∥ = ∥w∥?Given vectors v and w in R^n, if their norms are equal (∥v∥ = ∥w∥), we can demonstrate that v⋅w and v⋅(v−w) are both equal to zero, indicating that v−w and v⋅w are orthogonal.
To prove this, we start with the dot product v⋅w. Using the properties of the dot product, we have v⋅w = ∥v∥ ∥w∥ cosθ, where θ is the angle between v and w. Since ∥v∥ = ∥w∥, the expression simplifies to v⋅w = ∥v∥^2 cosθ. If ∥v∥ = ∥w∥, it implies that ∥v∥^2 = ∥w∥^2, and thus, cosθ = 1.
As cosθ = 1, the dot product v⋅w becomes v⋅w = ∥v∥^2, which is equal to zero. Therefore, v⋅w = 0, indicating that v and w are orthogonal.
Next, we consider the dot product v⋅(v−w). Expanding this expression, we have v⋅(v−w) = v⋅v − v⋅w. Since v⋅w is zero (as shown earlier), the dot product simplifies to v⋅(v−w) = v⋅v = ∥v∥^2, which is again zero when ∥v∥ = ∥w∥.
Hence, we have demonstrated that v⋅w = 0 and v⋅(v−w) = 0 when ∥v∥ = ∥w∥, confirming that v−w and v⋅w are orthogonal.
Learn more about orthogonality
brainly.com/question/32196772
#SPJ11
For vectors v and w with equal magnitudes, v w and v - w are orthogonal because the dot product equals zero, as proved step by step using properties of dot products and magnitudes.
Explanation:In the field of linear algebra, the given question aims to prove that if for vectors v and w if the magnitudes are equal i.e. ∥v∥ = ∥w∥, then the vectors v w and v − w are orthogonal.
We'll prove this by showing that their dot product equals zero. For two vectors to be orthogonal, the dot product must be zero.
Given, ∥v∥ = ∥w∥, square both sides will give ∥v∥^2 = ∥w∥^2.In terms of their dot products, this equation becomes v • v = w • w.Next, calculate the dot product of v w and v − w. This will give v w • (v - w) = v • v - v • w which we know equals zero because v • v equals w • w.Hence, we have now proved that v w and v − w are indeed orthogonal.
Learn more about Orthogonal Vectors here:https://brainly.com/question/31971350
#SPJ12
Parallel lines EN, BH, and RK, with transversal PW are shown. m/BMV-108 and m/KVS-72.
Part A: Based on the diagram above and the given information, what is the
m/WPN?

Answers
The value of measure of angle WPN is,
⇒ m ∠WPN = 108°
We have to given that;
Parallel lines EN, BH, and RK, with transversal PW are shown.
And, m ∠ BMV = 108° and m ∠KVS = 72°
Now, We get by definition of vertically opposite angle;
m ∠ BMV = m ∠PWN = 108°
Hence, By definition of alternate angle we get;
⇒ m ∠PWN = m ∠WPN = 108°
Thus, The value of measure of angle WPN is,
⇒ m ∠WPN = 108°
Learn more about the angle visit:;
https://brainly.com/question/25716982
#SPJ1
pls help i cant fugure it out and question is on picture

Answers
Answer:
Step-by-step explanation:
According to the figure, cos Ф = 16/20 = 4/5 = 0.80.
Using the inverse cosine function on a calculator, we get
Ф = 0.644 radians or 36.87 degrees or arccos 4/5
Make v the subject of the relation KE = ½mv²
Answers
Answer:
\(v=\sqrt{\frac{2KE}{m} }\)
Step-by-step explanation:
\(KE = 1/2mv^2\)
\(KE/1/2=mv^2\)
\(2KE=mv^2\)
\(2KE/m=v^2\)
\(\sqrt{2KE/m} =v\)
a researcher obtain a statistically significant r=-.91 when n=30. how would you report this?
Answers
A statistically significant negative correlation coefficient of r = -0.91 was obtained from a sample of n = 30. This indicates a strong and significant negative relationship between the variables.
The researcher conducted a correlation analysis and found a correlation coefficient (r) of -0.91, which indicates a strong negative relationship between the variables under investigation. The negative sign indicates that as one variable increases, the other variable tends to decrease, and vice versa.
The statistical significance of the correlation coefficient is crucial in determining whether the observed relationship is likely to be due to chance or if it truly exists in the population. In this case, the report should highlight that the obtained correlation coefficient is statistically significant.
To establish statistical significance, the researcher likely conducted a hypothesis test, such as a t-test or a permutation test, to determine the probability of obtaining a correlation coefficient as extreme as -0.91 under the null hypothesis of no correlation. Since the obtained correlation coefficient is statistically significant, it suggests that the observed negative relationship is unlikely to be a result of chance and provides evidence for a genuine association between the variables in the population from which the sample was drawn.
Reporting this finding is important for conveying the strength and significance of the negative relationship to the readers, providing valuable insights for further analysis and interpretation of the variables under investigation.
Learn more about correlation coefficient here:
https://brainly.com/question/29704223
#SPJ11
Hassam buys two adult tickets and two child tickets.
The booking agency charges an extra 5% of the total cost as a booking fee.
Work out how much Hassam pays altogether.
Answers
Okay, here are the steps:
* Hassam buys 2 adult tickets and 2 child tickets
* Let's assume:
** Adult ticket price = $50
** Child ticket price = $25
* So total ticket price = 2 * $50 + 2 * $25 = $200
* The booking fee is 5% of the total cost
* 5% of $200 is $10
* So total payment = $200 + $10 = $210
Therefore, the total Hassam pays altogether is $210
What is the absolute value of -7? 7 - 1/7 1/7
Answers
Answer:
7
Step-by-step explanation:
First ones 7 second ones 7 third ones 1/7 forth ones 1/7
Step-by-step explanation:
Because absolute value basically means the distance from zero so the distance from zero from -7 is 7 the same with 7 and the distance from zero with -1/7 is you guested it 1/7 and follow suit for 1/7 and you got your answers
Hope this helps ;)
True/False: Money that is usable can be easily moved from your home to the store.
Answers
Answer:
true
Step-by-step explanation:
If the product of the extremes is 8,then the geometric mean is
~2
~4
~2(square root sign)2

Answers
The geometric mean of two numbers is the square root of their product:
\(GM(a,b)=\sqrt{ab}\)
So, if the product is 8, the geometric mean is \(\sqrt{8}=2\sqrt{2}\)
875²-125² factorise the following fully
Answers
Answer:
750000
Step-by-step explanation:

Please help! (slopes and grafts) (multiple choice)

Answers
Answer:
slope = 2
Step-by-step explanation:
Chau made $252 for 18 hours of work.
At the same rate, how much would he make for 9 hours of work?
Answers
Answer:
$126.00
Step-by-step explanation:
divde by 2
Now we apply the following equation to a problem in which time is neither given nor asked for.
vx2=v0x2+2ax(x−x0)
A sports car is sitting at rest in a freeway entrance ramp. The driver sees a break in the traffic and floors the car’s accelerator, so that the car accelerates at a constant 4.9 m/s2 as it moves in a straight line onto the freeway. What distance does the car travel in reaching a freeway speed of 30 m/s?
1. What distance has the car traveled when it has reached a speed of 22 m/s ?
Answers
The distance the car travels when it reaches a speed of 22 m/s can be calculated using the equation vx^2 = v0x^2 + 2ax(x - x0). Plugging in the given values, we can determine the distance to be 123.27 meters.
To find the distance traveled by the car when it reaches a speed of 22 m/s, we can use the equation vx^2 = v0x^2 + 2ax(x - x0), where vx is the final velocity, v0x is the initial velocity, a is the constant acceleration, x is the final position, and x0 is the initial position.
Given that the car is initially at rest (v0x = 0 m/s) and accelerates at a constant rate of 4.9 m/s^2, we can plug these values into the equation. Solving for x, we have vx^2 = 22^2 m^2/s^2 and substituting the values into the equation, we find:
22^2 = 0 + 2(4.9)(x - 0)
484 = 9.8x
x = 484/9.8 ≈ 49.39 m
Therefore, when the car reaches a speed of 22 m/s, it has traveled approximately 49.39 meters.
Learn more about eequation hhere:
https://brainly.com/question/29657983
#SPJ11
A small school with 60 total students records how many of their students
attend school on each of the 180 days in a school year. The mean number of students in attendance daily is 55 students and the standard deviation is 4 students. Suppose that we take random samples of 5 school days and
calculate the mean number of students in attendance on those days in each sample.
Calculate the mean and standard deviation of the sampling distribution of T.
You may round to one decimal place.
Mx=
Ox=
Answers
The mean of the sampling distribution of the sample means is 55 and the standard deviation is approximately 1.79 (rounded to one decimal place).
What is Standard deviation?Standard deviation is a measure of the amount of variation or dispersion of a set of data values from its mean or expected value. It is a statistic that represents how spread out the data is from the mean.
The standard deviation is calculated by taking the square root of the variance, which is the average of the squared differences of each data point from the mean. The standard deviation is expressed in the same units as the data and is usually denoted by the symbol "σ" (sigma) for a population or "s" for a sample.
In the given question,
We can start by using the properties of the mean and standard deviation of a sampling distribution:
The mean of the sampling distribution of the sample means (Mx) is equal to the population mean (μ), which is given as 55.
The standard deviation of the sampling distribution of the sample means (Ox) is equal to the population standard deviation (σ) divided by the square root of the sample size (n), i.e.,
Ox = σ / sqrt(n)
where n = 5 (the sample size) and σ = 4 (the population standard deviation).
Substituting these values into the formula, we get:
Ox = 4 / sqrt(5) ≈ 1.79
Therefore, the mean of the sampling distribution of the sample means is 55 and the standard deviation is approximately 1.79 (rounded to one decimal place).
To know more about Standard deviation,visit:
https://brainly.com/question/23907081
#SPJ1
5. For the following problems, using the Big M method, construct the complete first simplex tableau for the simplex method. Identify the initial entering basic variable and the leaving basic variable.
Minimize Z = 2x₁ + 3x₂ + x₃
subject to
x₁ + 4x₂ + 2x₃ ≥ 8
3x₁ + 2x₂ ≥ 6
and
x₁ ≥ 0, x₂ ≥ 0, x₃ ≥ 0.
Answers
The Big M method is a technique used in linear programming to solve problems with constraints and objective functions. It is an extension of the simplex method that handles cases where some constraints have strict inequalities (i.e., ">") or the objective function includes a term to be minimized.
To construct the first simplex tableau using the Big M method, follow these steps:
1. Write the objective function in standard form:
\(Z = 2x₁ + 3x₂ + x₃\)
2. Introduce slack variables to convert the inequalities into equations:
\(x₄ = 8 - x₁ - 4x₂ - 2x₃\\x₅ = 6 - 3x₁ - 2x₂\)
3. Add a big M term to the objective function for each slack variable:
\(Z = 2x₁ + 3x₂ + x₃ + M₁x₄ + M₂x₅\)
4. Convert the inequalities into equations by adding surplus variables for ">=" constraints:
\(x₆ = x₁ + 4x₂ + 2x₃ - 8\\x₇ = 3x₁ + 2x₂ - 6\)
5. Add a big M term to the objective function for each surplus variable:
\(Z = 2x₁ + 3x₂ + x₃ + M₁x₄ + M₂x₅ + M₃x₆ + M₄x₇\)
6. Write the initial simplex tableau using the augmented matrix:
```
[ 2 3 1 0 0 0 0 0 ]
[ -1 -4 -2 1 0 0 0 8 ]
[ -3 -2 0 0 1 0 0 6 ]
[ 1 4 2 0 0 1 0 -8 ]
[ 3 2 0 0 0 0 1 -6 ]
```
7. Identify the entering and leaving basic variables:
- The entering variable is the column with the most negative coefficient in the objective row.
In this case, it is the second column (x₂).
- The leaving variable is the row with the smallest non-negative ratio of the right-hand side to the entering variable's coefficient.
In this case, it is the third row (x₆).
Know more about Big M method here:
https://brainly.com/question/32968890
#SPJ11
Using the Big M method, the complete first simplex tableau for the given linear programming problem is constructed as follows:
┌─────────────┬──────┬───────┬───────┬─────┬─────┬─────────────┐
│ BV │ x₁ │ x₂ │ x₃ │ s₁ │ s₂ │ RHS │
├─────────────┼──────┼───────┼───────┼─────┼─────┼─────────────┤
│ Z │ 2 │ 3 │ 1 │ 0 │ 0 │ 0 │
├─────────────┼──────┼───────┼───────┼─────┼─────┼─────────────┤
│ x₁ + 4x₂ + │ 1 │ 4 │ 2 │ -1 │ 0 │ -8 │
│ 2x₃ - M │ │ │ │ │ │ │
├─────────────┼──────┼───────┼───────┼─────┼─────┼─────────────┤
│ 3x₁ + 2x₂ │ 3 │ 2 │ 0 │ 0 │ -1 │ 6 │
├─────────────┼──────┼───────┼───────┼─────┼─────┼─────────────┤
│ x₁ │ 1 │ 0 │ 0 │ 1 │ 0 │ 0 │
├─────────────┼──────┼───────┼───────┼─────┼─────┼─────────────┤
│ x₂ │ 0 │ 1 │ 0 │ 0 │ 1 │ 0 │
├─────────────┼──────┼───────┼───────┼─────┼─────┼─────────────┤
│ x₃ │ 0 │ 0 │ 1 │ 0 │ 0 │ 0 │
└─────────────┴──────┴───────┴───────┴─────┴─────┴─────────────┘
The initial entering basic variable is x₁, which has the most negative coefficient in the objective row. The leaving basic variable is x₃, determined by selecting the row with the smallest positive ratio of the right-hand side (RHS) to the entering column's coefficient. In this case, the ratio for the fourth row (0/1) is the smallest, so x₃ leaves the basis.
To construct the complete first simplex tableau using the Big M method, we first convert the given problem into standard form by introducing slack variables (s₁ and s₂) for the inequalities and a large positive value (M) to penalize the artificial variable in the objective function.
The first row represents the objective function, where the coefficients of the decision variables x₁, x₂, and x₃ are taken directly from the given problem. The slack and artificial variables (s₁ and s₂) have coefficients of 0 since they don't appear in the objective function.
The subsequent rows represent the constraints. Each row corresponds to one constraint, where the coefficients of the decision variables, slack variables, and the artificial variable are taken from the original problem. The right-hand side (RHS) values are also copied accordingly.
The initial entering basic variable is determined by selecting the most negative coefficient in the objective row, which is x₁ in this case. The leaving basic variable is determined by finding the smallest positive ratio of the RHS to the entering column's coefficient. Since the ratio for the fourth row (0/1) is the smallest, x₃ leaves the basis.
The resulting tableau serves as the starting point for applying the simplex method to solve the linear programming problem iteratively.
Learn more about Big M method:
https://brainly.com/question/32588617
#SPJ11
One afternoon, 10 inches of snow fell in 1 1/4 hours. At this rate, how many inches of snow fall in 1 hour?
USE THE PICTURE BELOW PLEASE
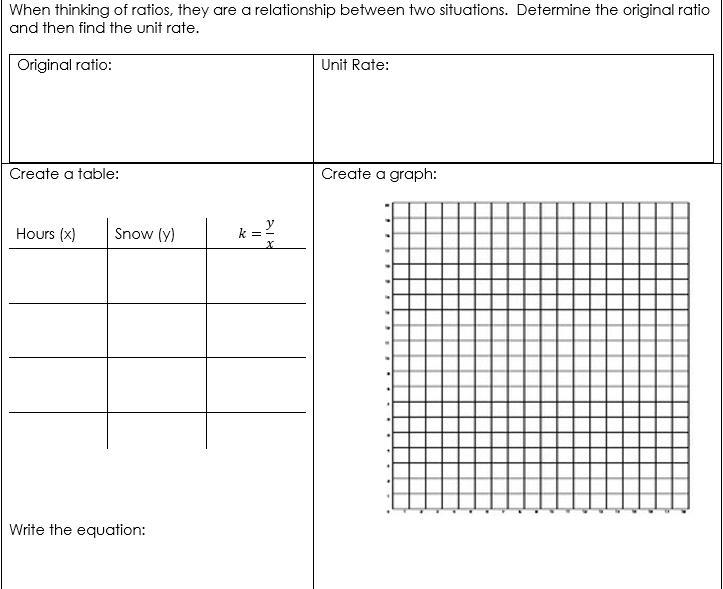
Answers
Answer:
The rate of snowfall can be computed as inches of snow per hour.
rate = 10 inches / (1.25 hours).
The denominator is the improper fraction 5/4. To divide by 5/4, you multiply numerator bky 4/5...REMEMBER?
4/5 OF TEN EQUALS 8; THE RATE IS 8 inches/HOUR.
Step-by-step explanation:
please help!! answer the question below

Answers
Answer:
Below
Step-by-step explanation:
Similar triangles due to A - A - A
Set up ratios
QR is to RS as QP is to TS
(x+2) / (2x-5) = 3/5 Cross multiply to get
5x+10 = 6x-15 subtract 5x from both sides of the equation
10 = x - 15 add 15 to both sides
25 = x
What is the first step in solving the equation b=r + 27 for r? A Add 21 to both sides. B Subtract 271 from both sides. C Multiply both sides by 2n. D Divide both sides by 27.

Answers
Answer:
B. Subtract 2π from both sides.
Step-by-step explanation:
In order to solve for r, you are gonna want to isolate it. To do so, you first have to subtract 2π from both sides.
Let f(x)=ax+b and (fof)(x)=4x+8 find the possible value of a and b and also find f(x)?
Answers
Answer:
\(\huge\boxed{f(x)=-2x-8\ \text{or}\ f(x)=2x+\dfrac{8}{3}}\)
Step-by-step explanation:
\(f(x)=ax+b\\\\(f\circ f)(x)=a(ax+b)+b=a^2x+ab+b\\\\(f\circ f)(x)=4x+8\\\Downarrow\\a^2x+ab+b=4x+8\Rightarrow a^2=4\ \wedge\ ab+b=8\\\\a^2=4\to a=\pm\sqrt4\to a=\pm2\\\\\text{for}\ a=-2:\\-2b+b=8\\-b=8\\\boxed{b=-8}\\\\\text{for}\ a=2:\\2b+b=8\\3b=8\\\boxed{b=\frac{8}{3}}\)
man buys 300 articles at 4 for $6 and sold all of them at $2 each; find:
i)the profit made by the man on selling one article
(ii) his total profit on selling all the 300 articles
Answers
The man buys 300 articles at 4 for $6, which means that he pays:
$6 for every 4 articles, or $1.50 per article.
The man then sells all 300 articles at $2 each, which means that he earns:
$2 for every article.
To find the man's profit, we need to subtract his cost from his revenue. His cost is the amount he paid for the 300 articles, which is:
300 articles * $1.50 per article = $450
His revenue is the amount he earned from selling the 300 articles, which is:
300 articles * $2 per article = $600
So his profit is:
$600 - $450 = $150
To find the profit made by the man on selling one article, we can divide his total profit by the number of articles he sold:
$150 / 300 articles = $0.50 per article.
Therefore, the man's profit on selling one article is $0.50
The drama club is selling tickets to their play to raise money for the show's expenses. Each student ticket sells for $4 and each adult ticket sells for $8. The auditorium can hold a maximum of 70 people. The drama club must make no less than $400 from ticket sales to cover the show's costs. Also, they can sell at most 50 adult tickets. If xx represents the number of student tickets sold and yy represents the number of adult tickets sold, write and solve a system of inequalities graphically and determine one possible solution.
Answers
The system of inequalities for the given situation is
x +y ≤ 70.
$4x + $8x ≤ $400.
y ≤ 50.
And one possible solution is (40,30) and the graph of the inequality is attached below.
Inequality:
Inequality refers the non equal comparison of the expressions.
Given,
The drama club is selling tickets to their play to raise money for the show's expenses. Each student ticket sells for $4 and each adult ticket sells for $8. The auditorium can hold a maximum of 70 people. The drama club must make no less than $400 from ticket sales to cover the show's costs. Also, they can sell at most 50 adult tickets.
Here we need to find the system of inequalities graphically and also determine one possible solution for it.
Let us consider x represents the number of student tickets sold and y represents the number of adult tickets sold.
Therefore, in here we know that, they can sell at most 50 adult tickets.
Which means that the value of y can't be greater than 50.
So, in inequality it can be written as,
y ≤ 50.
And the total number of seats in the auditorium is 70.
Therefore,
x + y ≤ 70
And we also know that, they sells the ticket at the cost not less than $400.
So,
$4x + $8x ≤ $400.
Now, we have to plot those inequality on the graph, the we get he following graph.
In the graph, the blue line represents the inequality x + y ≤ 70 and the red line represents the inequality $4x + $8x ≤ $400.
While we looking into the graph we have identified that the solution of the graph is (40,30).
Which means there are 40 number of students and 30 number of adults.
To know more about Inequality here.
https://brainly.com/question/28823603
#SPJ1

Fill in the table using this function rule.
y=17 - 2x
x
х
у
1
2
3
D
D
.
5
Х
$
? HELP ME PLEASE……………………………………………….

Answers
Answer:
15, 13, 11, 7
Step-by-step explanation:
i) x= 1
then
y= 17-2(1)
y= 17-2
y= 15
.
.
.
.
.
67 16 ft y
What is the value of y in the triangle? Round your final answer to the nearest hundredth.

Answers
a^2 + b^2 = c^2
16^2 + 67^2 = c^2
256 + 4489 = 4745
to undo the squared, you find the square root of 4745 and its 68.88 rounded
sum1 help!! this questions been killing me love yah on whoever helps mwah kisses <333

Answers
Answers:
A.
C.
F.
I think that is all of them.
Answer: Its E And A
Step-by-step explanation:
What is the value of f(-5) if f (x) = -x-4
Answers
Answer:
x=1
Step-by-step explanation:
Find the slope of the line below:
Find the slope using the table below:

Answers
Answer:
ill just help you out with this-
the slopes are
5/4 and 7
Step-by-step explanation:
so for question number 7 there are black dots right? those indicate that theyre exact points (because sometimes in a graph you dont know if its 6 or 6.1, cause sometimes theyre very close)
so the point on the left side is (-2, -2) because x is on the left side of the y axis (the vertical line). since its below the x axis (the horizontal line) its negative
for the point on the right its the opposite, because x is on the right x is positive. because x is above the x axis, its positive (but it can also be positive if its on the x axis, x = 0)
the point on the right is (2, 3)
so we substitute these points into the equation for the slope
3 - (-2) / 2 - (-2) it doesnt matter which way you put them, but if you put the first y (-2, 2) (the 2) then you have to put the x from the first point
but anyways
3 - (-2) / 2 - (-2)
simplify:
3 + 2 / 2 + 2
5 / 4
so the slope is 5/ 4
run 5 rise 4
for the graph..the graph is really easy lol i like graphs
but anyways for the graph the points are already given
when x is 2, y is 14
when x is 5, y is 35
when x is ____, y is blah blah blah
so now all you have to do is substitute two points into the equation. it doesnt matter which points because the slope will still be the same for example:
you can substitute (2, 14) and (5, 35)
35 - 14/ 5 - 2
21 / 3
7
and you can also substitute (5, 35) and (10, 70)
70 - 35/ 10 - 5
35 / 5
7
and its still the same slope
Answer: five/four
7
Step-by-step explanation:
Subtract 14 from 35 to get 21. 21/
five minus two is 3
21/3 = 7