Bill will randomly pick one marker a bag and one crayon from another bag.There are three red markers, 2 green markers , and 1 blue marker in the first bag.There are 2 brown crayons and 3 purple crayons in the bag. What is the probabilityt of picking a red marker and a purple crayon?
Answers
Answer:
i believe it is 2/6
Step-by-step explanation:
Answer:
red marker= 3/6
purple crayon= 3/5
Related Questions
1. Find x if m∠2 = 4x + 5 and m∠1 = 5x − 2.
2. M∠1 = 7x + 7 and m ∠AMH = 16x + 4. Find m∠1.
3. Find m∠2 if m∠2 = 7x + 5 and m∠1 = 9x − 5.
Answers
1) The value of measure of x is, 7
2) The value of measure of angle 1 is,
∠ 1 = 42 degree
3) The value of measure of angle 2 is,
∠ 2 = 40 degree
We have,
A triangle AMH is shown in image.
Since, From figure we have,
By definition of angle bisector,
∠ 1 = ∠ 2
And, 2 ∠ 1 = ∠ AMH
Substitute all the given values, we get;
1) ∠ 1 = ∠ 2
5x - 2 = 4x + 5
Sole for x,
5x - 4x = 5 + 2
x = 7
2) 2 ∠ 1 = ∠ AMH
2 (7x + 7) = 16x + 4
14x + 14 = 16x + 4
14 - 4 = 16x - 14x
10 = 2x
x = 10/2
x = 5
Hence, Measure of angle 1,
∠ 1 = 7x + 7
∠ 1 = 7 (5) + 7
∠ 1 = 42 degree
3) ∠ 1 = ∠ 2
9x - 5 = 7x + 5
9x - 7x = 5 + 5
2x = 10
x = 5
Hence, Measure of angle 2 is,
∠ 2 = 7x + 5
∠ 2 = 7 (5) + 5
∠ 2 = 40°
Learn more about the triangle visit;
brainly.com/question/1058720
#SPJ4

suppose v is finite-dimensional, t 2 l.v / has dim v distinct eigenvalues, and s 2 l.v / has the same eigenvectors as t (not necessarily with the same eigenvalues). prove that st d ts.
Answers
As, stx = tsx for every eigenvector x of t, and eigenvectors corresponding to distinct eigenvalues are linearly independent, we can conclude that st = ts.
To prove that st = ts, where v is finite-dimensional, t and s are linear operators on v, t has dim v distinct eigenvalues, and s has the same eigenvectors as t (not necessarily with the same eigenvalues), we can use the fact that eigenvectors corresponding to distinct eigenvalues are linearly independent.
Let's consider an eigenvector x of t with eigenvalue λ. We can write this as tx = λx. Now, since s has the same eigenvectors as t, we can write this as sx = λx.
Now, let's consider the product stx. Using the definitions of s and t, we have stx = s(λx) = λ(sx).
Since sx = λx, we can substitute this in the above equation to get stx = λ(λx) = λ²x.
On the other hand, let's consider the product tsx. Using the definitions of s and t, we have tsx = t(λx) = λ(tx).
Since tx = λx, we can substitute this in the above equation to get tsx = λ(λx) = λ²x.
Since stx = tsx for every eigenvector x of t, and eigenvectors corresponding to distinct eigenvalues are linearly independent, we can conclude that st = ts.
Learn more about eigenvector eigenvalues https://brainly.com/question/15586347
#SPJ11
Show the calculating process by the restoring-division
algorithm for the following division case:
Divisor 00011
Dividend 1011
Answers
The quotient is 1111. The process continues until the result is less than the divisor.
To perform the division using the restoring-division algorithm with the given divisor and dividend, follow these steps:
Step 1: Initialize the dividend and divisor
Divisor: 00011
Dividend: 1011
Step 2: Append zeros to the dividend
Divisor: 00011
Dividend: 101100
Step 3: Determine the initial guess for the quotient
Since the first two bits of the dividend (10) are greater than the divisor (00), we can guess that the quotient bit is 1.
Step 4: Subtract the divisor from the dividend
101100 - 00011 = 101001
Step 5: Determine the next quotient bit
Since the first two bits of the result (1010) are still greater than the divisor (00011), we guess that the next quotient bit is 1.
Step 6: Subtract the divisor from the result
101001 - 00011 = 100110
Step 7: Repeat steps 5 and 6 until the result is less than the divisor
Since the first two bits of the new result (1001) are still greater than the divisor (00011), we guess that the next quotient bit is 1.
100110 - 00011 = 100011
Since the first two bits of the new result (1000) are still greater than the divisor (00011), we guess that the next quotient bit is 1.
100011 - 00011 = 100001
Since the first two bits of the new result (1000) are still greater than the divisor (00011), we guess that the next quotient bit is 1.
100001 - 00011 = 011111
Since the first two bits of the new result (0111) are less than the divisor (00011), we guess that the next quotient bit is 0.
011111 - 00000 = 011111
Step 8: Remove the extra zeros from the result
Result: 1111
Therefore, the quotient is 1111.
Learn more about divisor here
https://brainly.com/question/552761
#SPJ11
After 4 days Gianna made 215 cookies. After 6 days she made 275 cookies. How many cookies would Gianna make after 10 days?
Answers
Answer:
395 cookies are made after 10 days
Step-by-step explanation:
Gianna makes 30 cookies each day.
275-215= 60/2 =30
30*4= 120
275+120=395 cookies made after 10 days
Comparison of per capita annual income and annual rate of teenage pregnancy in massachusetts counties in 2012 was conducted. what type of study is this?
Answers
The Correlational Studies is the one adopted to make comparison of per capita annual income and annual rate of teenage pregnancy
What is a research study?This refers to a systematic, rigorous, & critical investigation or stuey that aims to answer questions.
The type of research study are:
Case StudiesCorrelational StudiesLongitudinal StudiesExperimental StudiesClinical Trial StudiesTherefore, the Correlational Studies is the one adopted to make comparison of per capita annual income and annual rate of teenage pregnancy in massachusetts counties in 2012
Read more about research study
brainly.com/question/968894
#SPJ4
In hypothesis testing, the critical value is O a. the probability of a Type II error b. the same as the p-value O c. the probability of a Type I error O d. a number that establishes the boundary of the rejection region
Answers
In hypothesis testing, the critical value is option (d) a number that establishes the boundary of the rejection region
The hypothesis testing is defined as the process of collecting the data and using that as inference draw the calculation about the population parameter.
The reject region of the hypothesis testing is defined as the set of values for the test statistic for which the null hypothesis is rejected.
Therefore, the critical value is a number that establishes the boundary of the rejection region of the graph
Hence, in hypothesis testing, the critical value is option (d) a number that establishes the boundary of the rejection region
Learn more about hypothesis test here
brainly.com/question/17099835
#SPJ4
Matlab Script Question
Please modify this script to run properly.
clear all
syms x
E = 10E6;
A = 0.5+(x/50); %function for A
xg = [0 5;5 10]; %Row for each element
ne = 2; %Number of Elements
nn = 3; %Total Number of Nodes
for i = 1:ne %Repeat this integration for each element
xe = xg(i,:); %Grab coordinates for this element
N = [(x-xe(2))/(xe(1)-xe(2)) (x-xe(1))/(xe(2)-xe(1))]; %Update N
B = diff(N,x); %Update B
Ke(:,:,i) = int(transpose(B)*A*E*B,x,xe(1),xe(2)); %Integrating K
fe(:,i) = int(transpose(N)*0,xe(1),xe(2)); %Integrating b(x).
end
%Assemble together
L(:,:,1) = [1 0 0 0 ; 0 1 0 0 ];
L(:,:,2) = [0 1 0 0 ; 0 0 1 0];
K = zeros(nn,nn);
f = zeros(nn,1);
for i = 1:ne
Le = L(:,:,i);
K = K + transpose(Le)*Ke(:,:,i)*Le;
f = f + transpose(Le)*fe(:,i);
end
%Apply BCs
K(1,:) = [];
K(:,1) = [];
f(4) = 5E3;
f(1) = [];
solution = double(inv(K)*f);
Answers
The modified script fixes variable initialization, integration limits, boundary conditions, and computation of the solution for a finite element problem in MATLAB.
The modified script is as follows:
clear all
syms x
E = 10E6;
A = 0.5+(x/50); %function for A
xg = [0 5;5 10]; %Row for each element
ne = 2; %Number of Elements
nn = 3; %Total Number of Nodes
Ke = zeros(nn, nn, ne); % Initialize Ke
fe = zeros(nn, ne); % Initialize fe
for i = 1:ne %Repeat this integration for each element
xe = xg(i,:); %Grab coordinates for this element
N = [(x-xe(2))/(xe(1)-xe(2)) (x-xe(1))/(xe(2)-xe(1))]; %Update N
B = diff(N,x); %Update B
Ke(:,:,i) = int(transpose(B)*A*E*B,x,xe(1),xe(2)); %Integrating K
fe(:,i) = int(transpose(N)*0,x,xe(1),xe(2)); %Integrating b(x).
end
%Assemble together
L = zeros(nn, nn, ne);
L(:,:,1) = [1 0 0 0 ; 0 1 0 0 ];
L(:,:,2) = [0 1 0 0 ; 0 0 1 0];
K = zeros(nn,nn);
f = zeros(nn,1);
for i = 1:ne
Le = L(:,:,i);
K = K + transpose(Le)*Ke(:,:,i)*Le;
f = f + transpose(Le)*fe(:,i);
end
%Apply BCs
K(1,:) = [];
K(:,1) = [];
f(3) = 5E3;
f(1) = [];
solution = double(inv(K)*f);
Changes made:
1. Initialized 'Ke' and 'fe' as zero matrices before the loop.
2. Changed the integration limits in the line 'fe(:,i) = int(transpose(N)*0,xe(1),xe(2));' to 'x, xe(1), xe(2)'.
3. Initialized 'L' as a zero matrix before the loop.
4. Adjusted the index of `f` to 'f(3)' instead of 'f(4)' since the size of 'f' is now 3.
5. Removed the first row and column of 'K' to apply boundary conditions.
6. Removed 'clear all' since it clears all variables, which may not be desired.
To know more about MATLAB, refer here:
https://brainly.com/question/30760537
#SPJ4
If f(x) = x - 3, g(x) = 3x - 9, and h(x) = x^2-6x+9, then (gf)(2)=

Answers
SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given functions
\(\begin{gathered} f(x)=x-3 \\ g(x)=3x-9 \\ h(x)=x^2-6x+9 \end{gathered}\)STEP 2: Find the gf(2)
\(\begin{gathered} \left(gf\right)\left(x\right)=g\left(x\right)f\left(x\right) \\ =g\left(2\right)f\left(2\right) \end{gathered}\)Find g(2)
\(\begin{gathered} x=2 \\ By\text{ substitution,} \\ g(2)=3(2)-9=6-9=-3 \end{gathered}\)Find f(2)
\(\begin{gathered} x=2 \\ By\text{ subsitution,} \\ f(2)=2-3=-1 \end{gathered}\)Find gf(2)
\(\begin{gathered} By\text{ multiplication,} \\ =-3\cdot-1=3 \end{gathered}\)Hence, the answer is 3
Please help me with this math assignment

Answers
Answer: A , C and F
Step-by-step explanation:
HELP PLZ can someone simplify this equation

Answers
7n² + 48n + 42
Combine like terms, -8n x -6n= 48n
-6 x -7= 42
Answer:
-49n^3 -n²+92n+42
Step-by-step explanation:
(7n²-8n-6)(-6n-7)
-42n^3-49n²+48n²+56n+36n+42
-49n^3 -n²+92n+42
Which statement is true? Question 1 options: A) – |–13| = 13 B) – |13| = 13 C) |–13| = 13 D) |13| = – 13
Answers
Answer:
The answer is C. |-13| = 13
Step-by-step explanation:
The definition of absolute value is:
\( \displaystyle \large{ |x| = \begin{cases} x \: \: (x \geqslant 0) \\ - x \: \: (x < 0) \end{cases}}\)
To say it simply, any real numbers in absolute sign, when evaluated, they will always be positive.
No matter the positive real numbers or negative real numbers - if these numbers are in absolute sign, they will be evaluated to positive.
Examples
\( \displaystyle \large{ |2| = 2} \\ \displaystyle \large{ | - 2| = 2} \\ \displaystyle \large{ | - 8| = 8} \)
But if the negative is not inside the absolute sign.
Examples II
\( \displaystyle \large{ - |2| = - 2} \\ \displaystyle \large{ - | - 2| = - 2} \\ \displaystyle \large{ - | - 8| = - 8} \)
First, we evalute the absolute value first. We know thay any real numbers in absolute sign will become positive. Next, after evaluating the absolute value, we simply add the negative symbol beside the positive number.
Simplified Definition
This one is to make it simple to remember.
\( \displaystyle \large{ |a| = a} \\ \displaystyle \large{ | - a| = a} \\ \displaystyle \large{ - |a| = - a} \\ \displaystyle \large{ - | - a| = - a}\)
After reading the explanation, see the choices and tell if they are true or not.
The A choice is wrong as we know that -|-13| is -13.
The B choice is wrong, the reason is same as the A choice.
The C choice is correct! Any real numbers in absolute sign are always positive.
The D choice is wrong because absolute-value numbers cannot be negative, refer to the C choice's reason.
Let me know if you have any questions!
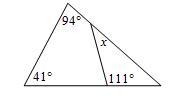
Use the screen shot to find the x
Answers
Answer:
69
Step-by-step explanation:
A triangle has a 180 degree angle so you do 180-111=69
Answer: x=24
Step-by-step explanation:
lets say 94 is ∠ a
41 is ∠ b
___ ∠ c
111∠ d
x ∠ e
so with that you will figure out that ∠ c is to find X
108-94-41= 45
so ∠ c is 45
now you can ∠a ∠ b∠ c
with that yo take
108-111-45=24
So X=24
Write a differential formula that estimates the change in volume of a sphere when the radius changes from
Answers
Answer:
d.
took the test
Step-by-step explanation:
toby is arranging books on a shelf. the shelf is 47 cm long to the nearest centimetre. each book is 2.5 cm wide to the nearest milimetre. show that toby can definalty fit 18 books on the shelf
Answers
Answer:
Yes, he can fit 18 books on the shelf.
Step-by-step explanation:
They will fit if maximum width of 18 books is less than minimum length of the shelf.
The minimum length of the shelf is 46.5 cm ( as its measured to nearest cm).
The maximum width of a book < 2.55 ( its measured to nearest 0.1 cm).
So multiplying width of books by 18 we get:
2.55*18 = 45.9 which is less than 46 so the answer is YES.
HELP PLEASE
what is the slope of the function

Answers
Answer:
1/2 probably
Step-by-step explanation:
For questions 8 - 15, use the following set of data to find the equation of the line of
best fit and assess the fit of the equation by plotting and analyzing residuals.
The data below show the mean swimming speed (m/s) of basking sharks of various
lengths (m)
Length (m) Speed (m/s) Predicted speed Residual
2.5
3
3.5
4.5
5
4.8
5.5
5.2
6
5.5
a Calculate the line of best fit Round a and b to the nearest hundredth.
Answers
Answer:
Y^= 1.767 + 0.6294X when rounded give s Y^= 1.77 +0.63X
b= 0.6294 rounded to 0.63
a= 1.77
The predicted lines are for each X and Y
3.340,3.96, 4.914, 5.228, and 5.543
Step-by-step explanation:
The data given is
Length (m) Speed (m/s) Predicted Line
2.5 3 3.340
3.5 4.5 3.96
5 4.8 4.914
5.5 5.2 5.228
6 5.5 5.543
The calculations are
Xsquare XY Y X
6.25 7.5 3 2.5
12.25 15.75 4.5 3.5
25 24 4.8 5
30.25 28.6 5.2 5.5
36 33 5.5 6
Total 109.75 108.85 23 22.5
The estimated regression line of Y on X is
Y^ = a +bX
and two normal equations are
∑Y = na + b∑X
∑XY= a∑X + b∑X²
Now X`= ∑X/ n= 22.5/5=4.5
Y`= ∑Y/ n= 23/5= 4.6
b= n∑XY- (∑X)(∑Y) / n∑X²- (∑X²)
Putting the values
b= 5(108.85) - (23)(22.5)/ 5(109.75)- (22.5)²
b= 544.25-517.5/ 548.75-506.25
b= 26.75 /42.5
b= 0.6294
and
a= Y`- bX~= 4.6- 0.6294(4.5)= 4.6-2.823= 1.767
Hence the
desired estimated regression line of Y on X is
Y^= 1.767 + 0.6294X
Y^= 1.77 +0.63X
The estimated regression co efficient b= 0.6294 indicates that the values of Y increase by 0.6294 units for a unit increase in X.

Which scatterplots have clusters? Check all that apply.

Answers
Answer:
the second one
there like all togehter
Step-by-step explanation:
Answer:
B and D
Step-by-step explanation:
Just did on edge2021
The hummingbird population on an island is declining at a rate of 1.4% per year. The population was 5500 in the year 2009.
What is the best prediction of the hummingbird population in the year 2016?
Enter your answer, rounded to the nearest integer, in the box.
The hummingbird population will be
Answers
Answer:
77
Step-by-step explanation:
I took the quiz
Answer:
The answer would be 77
Step-by-step explanation:
At age 45 when the deferred payments from his current contract ends, all-star shortstop Alex Rodriguez plans to have $230 million in savings from his baseball playing days. He wants two things from his savings: a 40-year ordinary annuity and $500 million at age 60 in order to purchase majority ownership in his native Miami's Florida Marlins. How large can his annual annuity payment be based on this information and assuming his savings can earn 8% annually after age 45 ? $6,069,727 $5,620,118 $6,906,832 $6,395,215
Answers
Therefore, the annual annuity payment can be approximately $6,069,727.
To calculate the size of the annual annuity payment, we can use the present value formula for an ordinary annuity. The formula is given by:
PMT = PV / [(1 - (1 + r)⁻ⁿ) / r]
Where:
PMT = Annual annuity payment
PV = Present value of the annuity
r = Annual interest rate
n = Number of periods
Given:
PV = $230 million
r = 8% = 0.08
n = 40 years
Using the formula, we can calculate the annual annuity payment:
PMT = 230,000,000 / [(1 - (1 + 0.08)⁻⁴⁰) / 0.08]
PMT ≈ $6,069,727
To know more about annual annuity payment,
https://brainly.com/question/31981614
#SPJ11
look carefully at the accompanying histogram. the histogram displays the grades received on an exam by students in a history course. from an inspection of this histogram, we can conclude that the mean or average exam score is expected to be:
Answers
According to the histogram, the expected mean exam score is approximately 6.5. This value is centered on the majority of scores, indicating that it is most likely the exam's average.
A histogram is a graph that shows data points arranged in user-defined ranges. By grouping a large number of data points into logical ranges or bins, the histogram, which looks like a bar graph, makes a data series easier to understand.
Histograms and bar charts both use columns to present a visual display, and the terms are frequently used interchangeably. However, technically speaking, a histogram depicts the frequency distribution of a data set's variables.
Learn more about histograms:
https://brainly.com/question/25983327
#SPJ4
Theorem 7.1.2 (Calculations with the Fourier transform)
Given f € L¹(R), the following hold:
(i) If f is an even function, then
f(y) = 2 [infinity]J0 f(x) cos(2πxy)dx.
(ii) If f is an odd function, then
f(y) = -2i [infinity]J0 f(x) sin(2πxy)dx.
Answers
(i) If f is an even function, then f(y) = 2 ∫[0,∞] f(x) cos(2πxy) dx.
(ii) If f is an odd function, then f(y) = -2i ∫[0,∞] f(x) sin(2πxy) dx.
The Fourier transform pair for a function f(x) is defined as follows:
F(k) = ∫[-∞,∞] f(x) \(e^{-2\pi iyx}\) dx
f(x) = (1/2π) ∫[-∞,∞] F(k) \(e^{2\pi iyx}\) dk
Now let's prove the given properties:
(i) If f is an even function, then f(y) = 2∫[0,∞] f(x) cos(2πxy) dx.
To prove this, we start with the Fourier transform pair and substitute y for k in the Fourier transform of f(x):
F(y) = ∫[-∞,∞] f(x) \(e^{-2\pi iyx}\) dx
Since f(x) is even, we can rewrite the integral as follows:
F(y) = ∫[0,∞] f(x) \(e^{-2\pi iyx}\) dx + ∫[-∞,0] f(x) \(e^{2\pi iyx}\) dx
Since f(x) is even, f(x) = f(-x), and by substituting -x for x in the second integral, we get:
F(y) = ∫[0,∞] f(x) \(e^{-2\pi iyx}\) dx + ∫[0,∞] f(-x) \(e^{2\pi iyx}\)dx
Using the property that cos(x) = (\(e^{ ix}\) + \(e^{- ix}\))/2, we can rewrite the above expression as:
F(y) = ∫[0,∞] f(x) (\(e^{-2\pi iyx}\) + \(e^{2\pi iyx}\))/2 dx
Now, using the definition of the inverse Fourier transform, we can write f(y) as follows:
f(y) = (1/2π) ∫[-∞,∞] F(y) \(e^{2\pi iyx}\) dy
Substituting F(y) with the expression derived above:
f(y) = (1/2π) ∫[-∞,∞] ∫[0,∞] f(x) \(e^{-2\pi iyx}\) + \(e^{2\pi iyx}\)/2 dx dy
Interchanging the order of integration and evaluating the integral with respect to y, we get:
f(y) = (1/2π) ∫[0,∞] f(x) ∫[-∞,∞] (\(e^{-2\pi iyx}\) + \(e^{2\pi iyx}\))/2 dy dx
Since ∫[-∞,∞] (\(e^{-2\pi iyx}\) + \(e^{2\pi iyx}\))/2 dy = 2πδ(x), where δ(x) is the Dirac delta function, we have:
f(y) = (1/2) ∫[0,∞] f(x) 2πδ(x) dx
f(y) = 2 ∫[0,∞] f(x) δ(x) dx
f(y) = 2f(0) (since the Dirac delta function evaluates to 1 at x=0)
Therefore, f(y) = 2 ∫[0,∞] f(x) cos(2πxy) dx, which proves property (i).
(ii) If f is an odd function, then f(y) = -2i ∫[0,∞] f(x) sin(2πxy) dx.
The proof for this property follows a similar approach as the one for even functions.
Starting with the Fourier transform pair and substituting y for k in the Fourier transform of f(x):
F(y) = ∫[-∞,∞] f(x) \(e^{-2\pi iyx}\) dx
Since f(x) is odd, we can rewrite the integral as follows:
F(y) = ∫[0,∞] f(x) \(e^{-2\pi iyx}\) dx - ∫[-∞,0] f(x) \(e^{-2\pi iyx}\) dx
Using the property that sin(x) = (\(e^{ ix}\) - \(e^{-ix}\))/2i, we can rewrite the above expression as:
F(y) = ∫[0,∞] f(x) \(e^{-2\pi iyx}\) - \(e^{2\pi iyx}\)/2i dx
Now, following the same steps as in the proof for even functions, we can show that
f(y) = -2i ∫[0,∞] f(x) sin(2πxy) dx
This completes the proof of property (ii).
In summary:
(i) If f is an even function, then f(y) = 2 ∫[0,∞] f(x) cos(2πxy) dx.
(ii) If f is an odd function, then f(y) = -2i ∫[0,∞] f(x) sin(2πxy) dx.
To know more about even function click here :
https://brainly.com/question/32608607
#SPJ4
Can someone help me with this. Will Mark brainliest.

Answers
Answer:
The lines are perpendicular.
Step-by-step explanation:
If the lines are parallel, then the slopes are equal
If the lines are perpendicular, then the slopes are negative reciprocals
If neither of the above occur, then the lines are neither parallel or perpendicular.
y = 2x + 3 is in slope-intercept form, so the slope = 2
2y + x = 6
Solve for y: 2y = -x + 6
y = -1/2(x) + 3 so the slope = -1/2
2 and -1/2 are negative reciprocals, so the lines are perpendicular.
Note: Negative reciprocals have a product of -1. 2(-1/2) = -1
1.Reshma wishes to mix two types of food P and Q in such a way that the vitamin contents of the mixture contain at least 8 units of vitamin A and 11 units of vitamin B. Food P costs Rs 60/kg and Food Q costs Rs 80/kg. Food P contains 3 units /kg of vitamin A and 5 units /kg of vitamin B while food Q contains 4 units /kg of vitamin A and 2 units /kg of vitamin B. Determine the minimum cost of the mixture?
Answers
Answer:
I don't forget you. ........
The community theater in Lowell has been seeing a 10% drop in attendance every year. If they sold 34,721 tickets this year, how many tickets can they expect to sell 2 years from now?If necessary, round your answer to the nearest whole number
Answers
Given that Lowell has been seeing a 10% drop in attendance every year.
The number of tickets sold this year is 34,721.
After one year, the number of tickets will reduce by 10%.
After one year, the number of tickets will be sell
\(=34721-10\text{ \% of 34721}\)\(=34721-\frac{10}{100}\times34721\)\(=31248.9\)After one year,31249 tickets will be sold.
After two year, the number of tickets will be sell
\(=31248.9-\frac{10}{100}\times31248.9\)\(=28124.01\)After two years from now, we can expect 28124 tickets will sell.
a person is standing next to a hot air balloon. at the same time, the person starts moving away from the balloon at 5 ft/sec and the balloon rises straight into the air at a rate of 12 ft/sec. is the distance between the person and the balloon increasing or decreasing 4 seconds after they start moving?
Answers
Comparing the distances at 3 seconds (39 ft) and 4 seconds (51.96 ft), we can conclude that the distance between the person and the balloon is increasing after 4 seconds.
Let's analyze the situation using the given terms "person", "moving", and "distance".
At the 4-second mark:
1. The person has moved horizontally away from the balloon at a rate of 5 ft/sec.
2. The balloon has risen vertically at a rate of 12 ft/sec.
To determine if the distance between the person and the balloon is increasing or decreasing, we can use the Pythagoras Theorem to find the diagonal distance between them.
After 4 seconds:
- The person has moved 5 ft/sec × 4 sec = 20 ft horizontally.
- The balloon has risen 12 ft/sec × 4 sec = 48 ft vertically.
Now, we can use the Pythagorean theorem to find the distance between the person and the balloon:
distance² = horizontal distance² + vertical distance²
At 4 seconds:
distance² = (20 ft)² + (48 ft)²
distance² = 400 + 2304
distance² = 2704
distance = √2704 ≈ 51.96 ft
Now let's check the distance at 3 seconds:
- The person has moved 5 ft/sec × 3 sec = 15 ft horizontally.
- The balloon has risen 12 ft/sec × 3 sec = 36 ft vertically.
distance² = (15 ft)² + (36 ft)²
distance² = 225 + 1296
distance² = 1521
distance = √1521 = 39 ft
Comparing the distances at 3 seconds (39 ft) and 4 seconds (51.96 ft), we can conclude that the distance between the person and the balloon is increasing after 4 seconds.
to learn more about Pythagoras Theorem click here:
https://brainly.com/question/343682
#SPJ11
(03.01 LC)
A theater company charges $5.50 per ticket for people of all age groups. If c represents the total number of children who bought tickets and a represents the total number of adults who bought tickets, which expression best represents the total money earned by the company from the sale of tickets? (1 point)
Answers
Answer: 5.50 (c + a)
Step-by-step explanation:
forty-seven percent of employees make judgments about their co-workers based on the cleanliness of their desk. you randomly select 8 employees and ask them if they judge co-workers based on this criterion. the random variable is the number of employees who judge their co-workers by cleanliness. which outcomes of this binomial distribution would be considered unusual? group of answer choices 0, 1, 8 0, 1, 7, 8 1, 2, 8 0, 1, 2, 8
Answers
The binomial distribution for this experiment would have a probability of 0.47 for each trial. Outcomes 0, 1, 7, and 8 would be considered unusual since they are unlikely to occur. The other outcomes (1, 2, 8) are more likely to occur.
The binomial distribution for this experiment is based on the probability of each trial, which is 0.47. This means that 47% of the time the outcome will be that the employee judges their co-workers by cleanliness, and 53% of the time it will not be the case. Outcomes 0, 1, 7, and 8 are unlikely to occur and therefore can be considered unusual. This is because they have a low probability of occurring. Outcomes 1, 2, and 8 are more likely to occur and have a higher probability of happening. The binomial distribution can be used to calculate the probability of each of these outcomes occurring. This probability can be used to determine which outcomes are more likely or unlikely to occur.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
Find the slope of the secant line between the values x 1and x ^2for the function given below. f(x)= −(3x+4)/5x+4;x 1=9,x ^2=4 The slope is Hint:
Answers
The slope of the secant line between x₁ = 9 and x₂ = 4 for the function f(x) = -(3x + 4)/(5x + 4) is -29/245.
To find the slope of the secant line between the values x₁ and x₂ for the function f(x) = -(3x + 4)/(5x + 4), we can use the formula for the slope of a secant line: slope = (f(x₂) - f(x₁)) / (x₂ - x₁). Given x₁ = 9 and x₂ = 4, we can substitute these values into the formula: slope = (f(4) - f(9)) / (4 - 9). To find f(4) and f(9), we substitute the respective values of x into the function: f(4) = -(3(4) + 4)/(5(4) + 4) = -16/24 = -2/3; f(9) = -(3(9) + 4)/(5(9) + 4) = -31/49.
Substituting these values into the slope formula: slope = (-2/3 - (-31/49)) / (4 - 9) = (-2/3 + 31/49) / (-5) = (29/49) / (-5) = -29/245. Therefore, the slope of the secant line between x₁ = 9 and x₂ = 4 for the function f(x) = -(3x + 4)/(5x + 4) is -29/245.
To learn more about slope click here: brainly.com/question/3605446
#SPJ11
line of best fit algebra: the number of steps per second that a runner takes is called the stride rate
Answers
The number of steps per second that a runner takes is not typically called the stride rate.
What is Stride Rate?Stride rate is a measurement of how frequently a person makes steps when walking or jogging. It is typically expressed in steps per minute and is calculated by dividing the total number of steps taken by the time it takes for each step to be completed. A person is often traveling faster if they have a greater stride rate. Numerous variables, such as a person's height, leg length, and muscular strength, can influence stride pace. The kind of exercise being done and the surface on which a person is walking or jogging might also have an impact. People may assess their development and modify their training plan to increase their speed and efficiency by keeping an eye on their stride rate.
To learn more about stride rate, visit:
https://brainly.com/question/28713848
#SPJ4
Determine whether the following sequence is arithmetic,
geometric, or neither.
1. 4, 1, 2
2. 4, 20, 100
3.212 106,53
Answers
=================================================
Explanation:
The sequence {4,1,2} is neither because both arithmetic sequences and geometric sequence are either always increasing or always decreasing. We start off decreasing when going from 4 to 1, but increase to 2.
----------
The sequence {4,20,100} is geometric because we multiply each term by 5 to get the next term. That means the common ratio is 5. Notice how this sequence is increasing.
---------
The sequence {212,106,53} is also geometric. This time the common ratio is 1/2 = 0.5; this sequence is decreasing.