Based on their appearance, match the images of the plane figures to their most correct name.Drag the tiles to the correct boxes to complete the pairs. Not all tiles will be used.
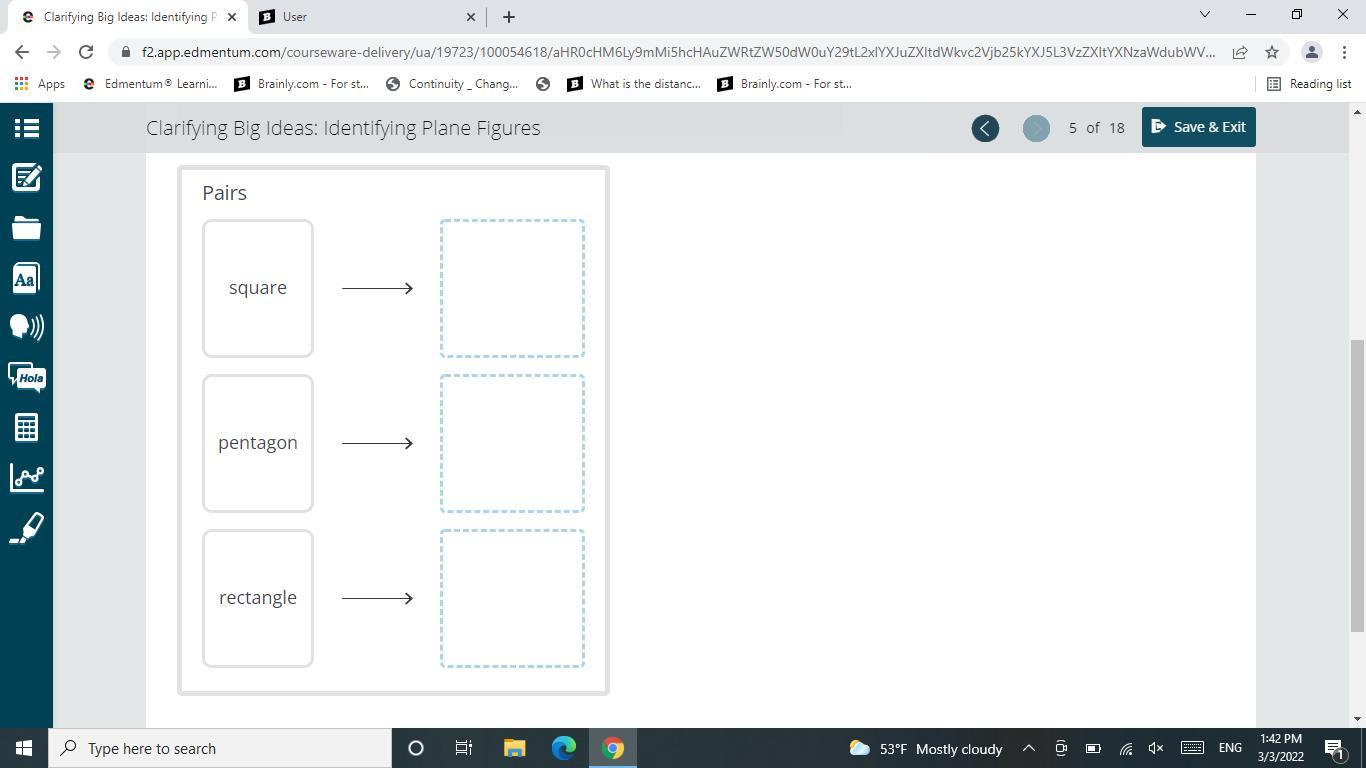
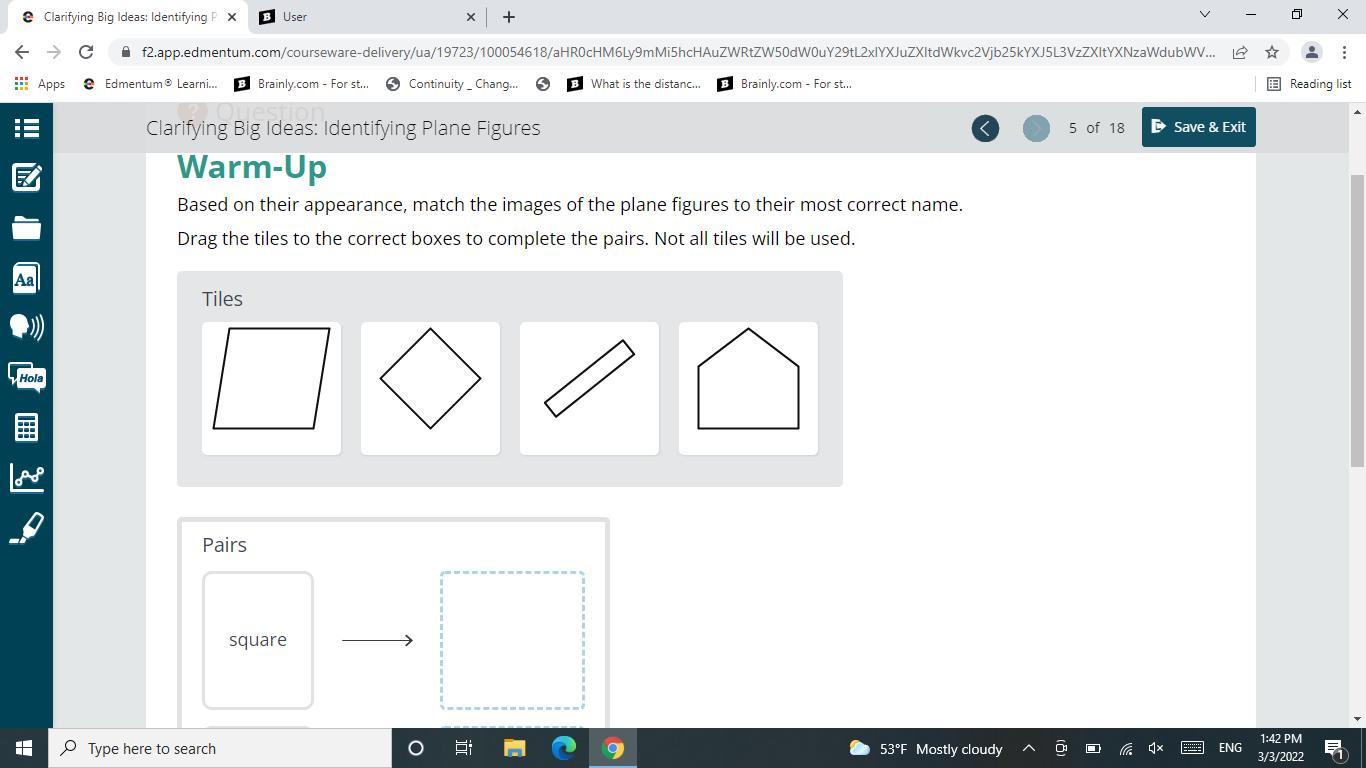
Answers
Solution
The following names of shapes are matched with the correct image
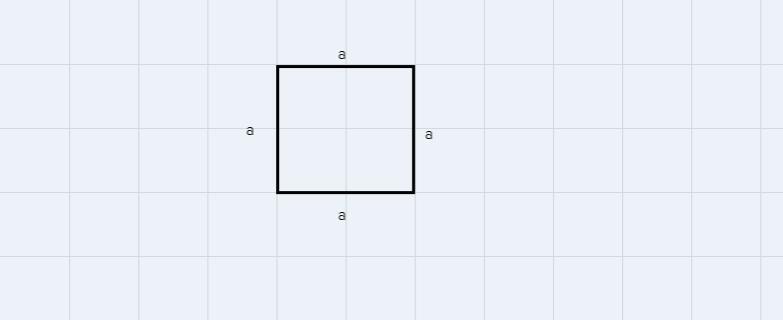
A square,
A square is a four sided quadilateral with all four sides equal.
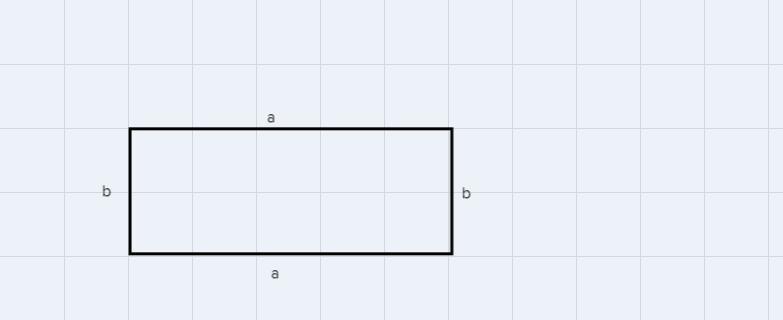
A rectangle,
A rectangle is a quadilateral with four sides and the opposite sides of a rectangle are equal.
A pentagon
A pentagon is any 5 sided polgon.
Related Questions
john likes to walk the steps of the department he works for during lunch break. There are s steps in his department. Today John would like to walk the steps of the taller building next door. The number of steps in the taller building next door is 27 less than 6 times the number of steps in John's department. Which expression represents the number of steps in the taller building next door in terms of s?
Answers
Mabel, Adeline and Charlie share 34500ft2 of land Mabel ownes 26%of the land area and Adeline Owens 47% of the land area . What is the land area that charlie owns ?
Answers
Answer:
Charlie owns 9,315 ft2 of the land area
Step-by-step explanation:
There are 34,500 ft2 of land shared between Mabel, Adeline, and Charlie.
Mabel owns 26% of the land area, that is:
26*34,500 ft2 / 100 = 8,970 ft2
Adeline owns 47% of the land area, or:
47*34,500 ft2 / 100 = 16,215 ft2
The land owned by Mabel and Adeline is: 8,970 ft2 + 16,215 ft2 = 25,185 ft2
Since the total area land is 34,500 ft2, Charlie owns:
34,500 ft2 - 25,185 ft2 = 9,315 ft2
Charlie owns 9,315 ft2 of the land area
surds and roots
look at picture

Answers
Answer:
\(12 - 4 \sqrt{5} \)
Step-by-step explanation:
\( {( \sqrt{10} - \sqrt{2} })^{2} \\ ( \sqrt{10} - \sqrt{2} )( \sqrt{10} - \sqrt{2} ) \\ 10 - 2 \sqrt{5} - 2 \sqrt{5} + 2 \\ 10 - 4 \sqrt{5} + 2 \\ 12 - 4 \sqrt{5} \)
I hope I helped you^_^
\( \huge \boxed{\mathfrak{Question} \downarrow}\)
Expand & simplify ⇨ \(( \sqrt{10} - \sqrt{2} ) ^{2} \). Give your answer in the form \(b - c \: \sqrt{5} \) where b & c are integers.\( \large \boxed{\mathbb{ANSWER\: WITH\: EXPLANATION} \downarrow}\)
\(( \sqrt { 10 } - \sqrt { 2 } ) ^ { 2 }\)
Use binomial theorem \(\left(a-b\right)^{2}=a^{2}-2ab+b^{2} \) to expand \(\left(\sqrt{10}-\sqrt{2}\right)^{2}\).
\(\left(\sqrt{10}\right)^{2}-2\sqrt{10}\sqrt{2}+\left(\sqrt{2}\right)^{2} \)
The square of \(\sqrt{10}\) is 10.
\(10-2\sqrt{10}\sqrt{2}+\left(\sqrt{2}\right)^{2} \)
Factor \(10=2\times 5\). Rewrite the square root of the product \(\sqrt{2\times 5} \) as the product of square roots \(\sqrt{2}\sqrt{5}\).
\(10-2\sqrt{2}\sqrt{5}\sqrt{2}+\left(\sqrt{2}\right)^{2} \)
Multiply \(\sqrt{2}\) and \(\sqrt{2} \) to get 2.
\(10-2\times 2\sqrt{5}+\left(\sqrt{2}\right)^{2} \)
Multiply -2 and 2 to get -4.
\(10-4\sqrt{5}+\left(\sqrt{2}\right)^{2} \)
The square of \(\sqrt{2}\) is 2.
\(10-4\sqrt{5}+2 \)
Add 10 and 2 to get 12.
\( \boxed{ \boxed{\bf\:12-4\sqrt{5} }}\)
Here, b & c are integers where \(\boxed{ \sf \: b = 12 \: and \: c = 4}\)The container that holds the water for the football team isfull. After pouring out 5 gallons of w2gallonsХ5?
Answers
Answer:
25 gallons
Explanation:
Let's call x the number of gallons that the container can hold.
The container starts half full, so it starts with (1/2)x gallons, then they pour out 5 gallons to let the container 3/10 full, so we need to subtract 5 gallons to get (3/10)x gallons. It means that we can write the following equation
\(\frac{1}{2}x-5=\frac{3}{10}x\)Now, we can solve the expression for x, so
\(\begin{gathered} \frac{1}{2}x-5+5=\frac{3}{10}x+5 \\ \frac{1}{2}x=\frac{3}{10}x+5 \\ \frac{1}{2}x-\frac{3}{10}x=\frac{3}{10}x+5-\frac{3}{10}x \\ \frac{1}{5}x=5 \\ 5\cdot\frac{1}{5}x=5\cdot5 \\ x=25 \end{gathered}\)Therefore, the container can hold 25 gallons.
4 3/8 + 5 1/2= in fractions
Answers
Answer:
9 7/8
Step-by-step explanation:
1. 4 3/8 can be converted into the improper fraction 35/8, and 5 1/2 can be converted into 11/2.
2. Now that we have 35/8 + 11/2, we have to find a common denominator. Since 2 goes into 8 four times, we can turn 11/2 into 44/8 by multiplying the numerator and denominator (the top and the bottom numbers) by 4.
3. Now we have 35/8 + 44/8. At this point, the all we have to do is add the numerators (the top numbers). 35+44=79, so our answer is 79/8, which we can simplify to 9 7/8.
please I need help with this

Answers
A. The following are sets A and B:
A = {2, 3, 5, 7, 11}
B = {1, 2, 3, 4, 6, 12}
C. Elements not in A or A' = ∅
B. The Venn diagram is attached
How to solve sets?A universal set is a set which consists of all elements related to the given sets. It is denoted by U.
A. Set A:
A = {2, 3, 5, 7, 11}
Set B:
B = {1, 2, 3, 4, 6, 12}
U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
A' = {1, 4, 6, 8, 9, 10, 12}
C. Elements not in A or A' = ∅
Complement of set A is refers to a set that contains the elements present in the universal set but not in set A.
Hence, the Venn diagram of sets A, B and U has been attached.
Read more on set theory:
https://brainly.com/question/13458417
#SPJ1

b) Use the graph to estimate the
value of x when y = 1
Answers
Answer:
Hey bro you're welcome.
Step-by-step explanation:
Which system of linear inequalities has the point (3, -2) in its solution set?
y < -3; y ≤ 2/3x - 4
y > -3; y ≥ 2/3x - 4
y < -3; y ≥ 2/3x - 4
y > -2; y ≤ 2/3x - 4
Answers
The system that has linear inequalities has the point (3, -2) in its solution set is y > -3; y ≥ 2/3x - 4.
We know that
If a ordered pair is a solution of the system of inequalities, then the ordered pair must satisfy both inequalities (makes true both inequalities)
In option B, we have
y > -3 ----> inequality A
y ≥ 2/3x - 4 ----> inequality B
In both inequality, change the values of x and y at the point (3, -2) and then compare the outcomes.
Inequality A
y > -3 ----> is true
Inequality B
y ≥ 2/3x - 4 ----> is true
Therefore
The ordered pair is a solution of the system B
As a result, the point (3, -2) in the solution set of the system with linear inequalities is y > -3; y 2/3x - 4.
To learn more about linear inequalities click here:
brainly.com/question/11897796
#SPJ4
Use the relationship represented in this Venn diagram to identify the true statement.
A. All trapezoids are rhombuses
B. All rhombuses are trapezoids
C. No trapezoids are rhombuses
D. No rhombuses are trapezoids
Answers
The true statement based on the relationship depicted in the Venn diagram is that no rhombuses are trapezoids (option D).
To identify the true statement using the relationship represented in the Venn diagram, we need to analyze the overlapping regions and the properties of the shapes involved.
A trapezoid is a quadrilateral with at least one pair of parallel sides, while a rhombus is a quadrilateral with all sides of equal length. Let's evaluate the options:
A. All trapezoids are rhombuses: This statement is not true based on the diagram. The overlapping region between the trapezoids and rhombuses shows that there are trapezoids that are not rhombuses. Therefore, option A is incorrect.
B. All rhombuses are trapezoids: This statement is true based on the diagram. The entire region representing rhombuses is also included within the region representing trapezoids. Every rhombus can be considered a trapezoid because it has at least one pair of parallel sides. Thus, option B is correct.
C. No trapezoids are rhombuses: This statement is not true based on the diagram. The overlapping region indicates that there are trapezoids that are indeed rhombuses. Therefore, option C is incorrect.
D. No rhombuses are trapezoids: This statement is true based on the diagram. There is no overlap between the regions representing rhombuses and trapezoids, implying that no rhombus can be considered a trapezoid. Hence, option D is correct.
for such more question on trapezoids
https://brainly.com/question/22351006
#SPJ8
A woman deposits $300 in a savings account that pays 6% annually. If she withdraws all the money in the account after 120 days, how much does she withdraw (rounded to the nearest dollar)?
Answers
The woman will withdraw $300 given 6% interest rate annually.
We can use the formula for simple interest to solve this problem:
I = Prt
where I is the interest earned, P is the principal (initial deposit), r is the annual interest rate as a decimal, and t is the time in years. Since the interest rate is given as an annual rate, we need to convert it to a daily rate by dividing by 365:
r = 0.06/365 = 0.00016438356
The time in years is 120/365 = 0.3287671233 years. Now we can plug in the values and solve for I:
I = 300 * 0.00016438356 * 0.3287671233 = 0.01699999999
The interest earned is $0.017, which is negligible. Therefore, the woman will withdraw the entire principal plus any interest earned, which is:
300 + 0.017 = $300.02
Rounding to the nearest dollar, the woman will withdraw $300.
To learn more about interest rate here:
https://brainly.com/question/29067327
#SPJ1
Kari worked twice as many hours as Chris. She also worked ten less than three times as many hours as Mark. Chris and Mark worked the same number of hours.
Answers
Answer:
Kari = 20 hours
Chris = 10
Mark = 10
Explanation:
K is Kari's hours
C is Chris's hours
Karis = 2 x C = K
Chris = C
Mark = C
3C - 10 = K
Assume C is 10 (since 10 is 1/3 of the hours mentioned)
2 x 10 = 20 so K worked 20 hours
20 is twice as much as 10 (C's hours)
and it's 30 - 10 (10 less than 3 times as many hours as Mark)
Write the equation of a line that goes through the point (2, 4) that is parallel to the
line y = 3x - 6.
Answers
Answer:
y = 3x - 2
Step-by-step explanation:
Parallel lines have the same gradient in this case 3 is the gradient.
We will use the point (2,4) to form our own equation.
4 will be y, 3 will be m, 2 will be x
All we need is to find the C in the equation y=mx + c
4 = 3(2) + c
4 = 6 + c
C = -2
Therefore;
y = 3x - 2
solve using substitution or elimination
6x-12y=0
x-6y=4
Answers

Analyze the graph of the function f(x) to complete the statement. On a coordinate plane, a curved line, labeled f of x, with a minimum value of (0, negative 3) and a maximum value of (negative 2.4, 17), crosses the x-axis at (negative 3, 0), (negative 1.1, 0), and (0.9, 0), and crosses the y-axis at (0, negative 3). f(x)<0 over and what other interval?
Answers
The interval where function f(x) is negative and greater than 0 is (-∞, -3) U (-1.1, 0)
We have,
The function f(x) crosses the x-axis at (-3, 0), (-1.1, 0), and (0.9, 0), it means that f(x) is negative for x values less than -3, between -1.1 and 0.9, and greater than 0.
Therefore, we can say that:
f(x) < 0 for x < -3 and -1.1 < x < 0.9
And,
The function f(x) has a minimum value of (0, -3) and a maximum value of (-2.4, 17).
This means that f(x) is positive for x values greater than -2.4. Therefore, we can say that:
f(x) > 0 for x > -2.4
Now,
Combining these inequalities, we can say that f(x) is negative over the intervals (-∞, -3) and (-1.1, 0.9), and positive over the interval (-2.4, ∞).
So,
The interval where f(x) is negative and greater than 0 is:
(-∞, -3) U (-1.1, 0)
Thus,
The interval where f(x) is negative and greater than 0 is (-∞, -3) U (-1.1, 0)
Learn more about functions here:
https://brainly.com/question/28533782
#SPJ1
31. Find the area of the shape below: 15m 3m (a) 87m² (b) 102m2 (c) 152m² (d) 18m² (e) 207m2 4m 6m 6m 3m

Answers
Hello!
see attachment
A1 = green
A2 = yellow
A3 = red
A1 = 15m * 3m = 45m²
A2 = (15m - (6m + 6m)) * 4m = 3m * 4m = 12m²
A3 = 15m * 3m = 45m²
A = A1 + A2 + A3
= 45m² + 12m² + 45m²
= 102m²
Answer:
b. 102 m²
Step-by-step explanation:
In order to find the area of shape.
Let's separate it into three rectangle.
We know that
Area of rectangle: Length*breadth
Using this
Area of left rectangle=15*3=45 m²
Area of middle rectangle=4*(15-6-6)=12 m²
Area of right rectangle= 15*3=45m²
Now
Total Area of shape= 45m²+12m²+45m²=102m²
person going to a party was asked to bring 3 different bags of chips. Going to the store, she finds 18 varieties.
How many different selections can she make?
Answers
Answer:
54
Step-by-step explanation:
Since their are 18 varieties and she needs 3 different bags, you would do 3*18, which is 54
So she can make 54 selections
ASAP! GIVING BRAINLIEST! Please read the question THEN answer correctly! No guessing. Show your work or give an explaination.

Answers
Answer:
The Answer is B
Step-by-step explanation:
Why, Because it is saying graph the equation by a number of units so it will most likely be going down. Hope it helps.
The sum of two numbers is 12. The difference of the two numbers is 6. What are the two numbers?
Answers
Answer:
3 and 9
Step-by-step explanation:
x+y=12
y-x=6
y-x=6
+x. +x
y=6+x
x+(6+x)=12
6+2x=12
-6. -6
2x=6
/2. /2
x=3
3+y=12
-3. -3
y=9
Hopes this helps please mark brainliest
which expression is equivalent to m-4/m+4 + (m+2) ?
A. m-4/(m+4)(m+2)
B. (m+4)(m+2)/m-4
C. m-4)(m+2)/m+4
D. m+4/(m-4)(m+2)
Answers
Answer:
C.
Step-by-step explanation:
......................
The expression that is equivalent to the expression (m - 4)/(m + 4) + (m + 2) is {m + m² + 6m + 4}/{m + 4}.
What is algebraic expression?An expression in mathematics is a combination of terms both constant and variable. For example, we can write the expressions as -
2x + 3y + 5
2z + y
x + 3y
Given is to find the expression is equivalent to -
(m - 4)/(m + 4) + (m + 2)
We have the following expression as -
(m - 4)/(m + 4) + (m + 2)
{(m - 4) + (m + 2)(m + 4)}/(m + 4)
{(m - 4) + m² + 4m + 2m + 8}/(m + 4)
{m + m² + 6m + 4}/{m + 4}
Therefore, the expression that is equivalent to the expression (m - 4)/(m + 4) + (m + 2) is {m + m² + 6m + 4}/{m + 4}.
To solve more questions on equivalent expression, visit the link-
https://brainly.com/question/1041084
#SPJ7
Triangle ABC is a 45*-45*-90* triangle where two vertices are A(-2,2) and B(-2,6) and AB is a leg of the triangle. What are all the possible ordered pairs for C?
Answers
Midpoint formula: [(x1 + x2) / 2, (y1 + y2) / 2]
For A(-2,2) and B(-2,6), the midpoint coordinates are:
C = [(-2 + -2) / 2, (2 + 6) / 2] = [-2, 4]
So, the only possible ordered pair for point C in this 45°-45°-90° triangle is (-2, 4).
This is a algebra thing and its my homework please answer those questions

Answers
Answer:
w or x
Step-by-step explanation:
the square root of 40 is 6.3
) Quantifier negation.
Form the negation of the following statements. Then apply De Morgan’s law and/or conditional law, when
applicable. Negation should appear only within predicates, i.e., no negation should be outside a quantifier
or an expression involving logical connectives. Show all steps.
a) ∀x (P(x) ∧ R(x))
b) ∀y∃z(¬P(y) → Q(z))
c) ∃x (P(x) ∨ (∀z (¬R(z) → ¬Q(z))))
Answers
The negations of the given statements with the application of De Morgan's law and/or conditional law.
a) ∃x (¬P(x) ∨ ¬R(x))
De Morgan's law:
∃y ∀z(¬P(y) ∧ ¬Q(z))
b) ∃y ∀z(¬P(y) ∧ ¬Q(z))
The double negation:
∃y ¬∃z(P(y) ∨ Q(z))
c) ¬∃x (P(x) ∨ (∀z (¬R(z)) → (∀z ¬Q(z))))
The conditional law:
¬∃x (P(x) ∨ (∀z (¬R(z)) → (∀z ¬Q(z))))
Let's form the negation of the given statements and apply De Morgan's law and/or conditional law, when applicable:
a) ∀x (P(x) ∧ R(x))
The negation of this statement is:
∃x ¬(P(x) ∧ R(x))
Now let's apply De Morgan's law:
∃x (¬P(x) ∨ ¬R(x))
b) ∀y∃z(¬P(y) → Q(z))
The negation of this statement is:
∃y ¬∃z(¬P(y) → Q(z))
Using the conditional law, we can rewrite the negation as:
∃y ¬∃z(¬¬P(y) ∨ Q(z))
c) ∃x (P(x) ∨ (∀z (¬R(z) → ¬Q(z))))
The negation of this statement is:
¬∃x (P(x) ∨ (∀z (¬R(z) → ¬Q(z))))
Using the conditional law, we can rewrite the negation as:
¬∃x (P(x) ∨ (∀z (R(z) ∨ ¬Q(z))))
Applying De Morgan's law:
¬∃x (P(x) ∨ (∀z ¬(¬R(z) ∧ Q(z))))
Simplifying the double negation:
¬∃x (P(x) ∨ (∀z ¬(R(z) ∧ Q(z))))
Using De Morgan's law again:
¬∃x (P(x) ∨ (∀z (¬R(z) ∨ ¬Q(z))))
For similar questions on De Morgan's law
https://brainly.com/question/28735989
#SPJ8
Which number, when rounded to the nearest tenth, is 43.6?

Answers
What is the 25th term of the Arithmetic Sequence: 4, -1, -6, -11 . . .
Answers
The 25th term of the arithmetic sequence is 148
What is a sequence?A sequence in which the difference between all pairs of consecutive numbers is equal is called an arithmetic progression.
The sequence given is 4, -1, -6, -11 . . .
Here a1 = 4
d = -1 -4 = -5
The formula to find the nth term of an arithmetic sequence is
an = a1 + (n - 1)d
Substituting the values
an = 4 + (n - 1)-5
We have to find the 25th term n = 25
a25 = 4 + (25 - 1)-5
a25 = 4 + (24)-5
a25 = 4 + (-144)
expanding the bracket
a25 = 148
Therefore, the 25th term is 148.
Learn more about sequence at:https://brainly.com/question/28036578
#SPJ
Select the correct answer from each drop-down menu. Each graph shows the results of a transformation applied to function f where f(x) = (1/2)^x.
Complete the statement given that g(x) =f(kx). The graph of function g is graph Because the graph a function g is the result of a  applied to the graph of function F .

Answers
Given that g(x) =f(kx). The graph of function g is graph Z Because the graph a function g is the result of a horizontal compression applied to the graph of function F.
What is a graph?A graph can be described as a pictorial representation or a diagram that represents data or values in an organized manner.
The graph of the function g(x) = f(kx) is obtained from the graph of f(x) by a horizontal compression or stretching, depending on the value of k.
In conclusion, If k is greater than 1, then the graph of g(x) is obtained from the graph of f(x) by a horizontal compression.
Learn more about graph of the function at: https://brainly.com/question/28643733
#SPJ1
What is the absolute deviation of 30 in this data set?
{26, 35, 27, 30, 22}
2
3
5
8
Answers
Using it's concept, it is found that the absolute deviation of 30 in the data set is of 2.
What is the absolute deviation of a measure?The absolute deviation of a measure is given by the absolute value of the differente between the measure and the mean.
The mean is the sum of all observations divided by the number of observations. In this data-set, it is given by:
M = (26 + 35 + 27 + 30 + 22)/5 = 28
30 - 28 = 2, hence, the absolute deviation of 30 in the data set is of 2.
More can be learned about absolute deviation at https://brainly.com/question/17381861
Answer:
The answer is 2
Step-by-step explanation:
I took the test
Solve the right triangle

Answers
lmk is anything is unclear. This would also work with cosine but it would have to be set up a little differently.

When grading English papers, the instructor checks every 4th paper for plagiarism. What form of sampling is used?
random
convenience
systematic
cluster
Answers
Answer: systematic
Step-by-step explanation:
In random sampling researcher choose elements randomly for sample .In convenience sampling individuals are selected as per his convenience and comfort.In systematic sampling individuals are selected in a systematic way by using a fix periodic interval k from the entire population .In cluster sampling clusters (of homogeneous elements) are selected to make a sample.Given, When grading English papers, the instructor checks every 4th paper for plagiarism which expresses a fixed periodic interval.
Hence, this is systematic sampling.
What must be true of the units in two rates if one rate can be converted to the units of the other rate? In other words, the units of the
first rate are both/all distinct from that of the converted rate, but it still represents the same measurement?
Answers
Answer:
Yes, unit of the first rate can be be different from and second and still represent the same measurement/value.
Step-by-step explanation:
Yes, if we have two units rate and one rate is converted to another, both measurement will still remain the same even after the conversion but the rate will be different.
For example if we want to convert $2 to naira, note that the unit rates for are distinct but after conversion the amount of both money will be the same.
If $1 = #386
2$ = 2×#386
$2 = #772
Hence the measurement of $2 is equivalent to 386 naira even though the rates are distinct (naira and $)
Convert from radians to degrees.
1/4π
Answers
1/4π radians is approximately equal to 45 degrees.
To convert a value from radians to degrees, multiply the value by 180/π. For example, to convert π/4 radians to degrees, multiply π/4 by 180/π to get 45 degrees. This conversion is useful for converting angles between the two units of measurement.
Degrees = Radians × 180/π.
Therefore, to convert 1/4π radians to degrees, we have:
Degrees = (1/4π) × (180/π) ≈ 45°
Hence, 1/4π radians is approximately equal to 45 degrees.
To know more about Conversion here
https://brainly.com/question/15743041
#SPJ1