ata yayincilik 4. deneme 8.sinif (2021) cevap anhtari vasa atabilirmisiniz
Answers
Answer:
what
Step-by-step explanation:
Related Questions
Suppose there is a 1.6 drop in temperature for every thousand feet that an airplane climbs into the sky. If the temperature on the ground is 55.2 ft what will be the temperature when the plane reaches an altitude of 5,000 ft?
Answers
The temperature when the plane reaches an altitude of 5,000 ft is 47.2.
What is temperature?Temperature is he degree of hotness and coldness in a body.
In this case, there is a 1.6 drop in temperature for every thousand feet that an airplane climbs into the sky.
The temperature at 5000 feet will be:
= 55.2 - 1.6(5000 / 1000)
= 55.2 - 1.6(5)
= 55.2 - 8
= 47.2
The temperature is 47.2
Learn more about temperature on:
brainly.com/question/24746268
#SPJ1
fill in the missing number: 0,1,1,2,3,5,8,13,-,34,55
Answers
The missing number of the series is 21.
The given sequence appears to follow the pattern of the Fibonacci sequence, where each number is the sum of the two preceding numbers. The Fibonacci sequence starts with 0 and 1, and each subsequent number is obtained by adding the two previous numbers.
Using this pattern, we can determine the missing number in the sequence.
0, 1, 1, 2, 3, 5, 8, 13, -, 34, 55
Looking at the pattern, we can see that the missing number is obtained by adding 8 and 13, which gives us 21.
Therefore, the completed sequence is:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.
To learn more about number here:
https://brainly.com/question/32210789
#SPJ4
The missing number in the sequence 0, 1, 1, 2, 3, 5, 8, 13, -, 34, 55 is 21.
To find the missing number in the sequence 0, 1, 1, 2, 3, 5, 8, 13, -, 34, 55, we can observe that each number is the sum of the two preceding numbers. This pattern is known as the Fibonacci sequence.
The Fibonacci sequence starts with 0 and 1. To generate the next number, we add the two preceding numbers: 0 + 1 = 1. Continuing this pattern, we get:
011235813213455Therefore, the missing number in the sequence is 21.
Learn more:About fill in here:
https://brainly.com/question/182137
#SPJ11
What is the domain of the graph?
a. (-2,-1,0,1,3}
b. -2
C.-3
d. (-3,-2, -1, 1, 3, 5)

Answers
Answer:
d is correct
Step-by-step explanation:
will mark brainliest! in kite UVWX, m

Answers
Answer:
52
Step-by-step explanation:
A $0.25 \mathrm{~kg}$ stone is held $11 \mathrm{~m}$ above the top edge of a water well and then dropped in. The well has a depth of $7.3 \mathrm{~m}$. Taking $y=0$ at the top edge of the well, calculate
(a) the gravitational potential energy of the stone-Earth system before the stone is released
(b) the gravitational potential energy of the stone-Earth system after the stone reaches the bottom of the well
(c) the change in gravitational potential energy of the system from when the stone is released to when it reaches the bottom of the well.
Answers
The gravitational potential energy of the stone-Earth system can be calculated before the stone is released, after it reaches the bottom of the well, and the change in gravitational potential energy during the process.
Gravitational potential energy is given by the formula PE = mgh, where m is the mass of the object, g is the acceleration due to gravity, and h is the height.
(a) Before the stone is released, it is held 11 m above the top edge of the well. The mass of the stone is 0.25 kg, and the acceleration due to gravity is approximately 9.8 m/s². Using the formula, the gravitational potential energy is calculated as PE = (0.25 kg)(9.8 m/s²)(11 m).
(b) After the stone reaches the bottom of the well, its height is 7.3 m. Using the same formula, the gravitational potential energy at this point is given by PE = (0.25 kg)(9.8 m/s²)(7.3 m).
(c) The change in gravitational potential energy can be determined by subtracting the initial potential energy from the final potential energy. The change in gravitational potential energy is equal to the gravitational potential energy after reaching the bottom of the well minus the gravitational potential energy before the stone was released.
By calculating these values, we can determine the specific numerical values for (a), (b), and (c) based on the given data.
Learn more about gravitational here:
https://brainly.com/question/32609171
#SPJ11
Lori wants to trade more than 3/10 but less than 4/5 of her stickers. which points on the line represents an amount she might trade? what fraction of the stickers might lori trade
Answers
Answer: To find the points on the line that represent the amount Lori might trade, we need to locate the points that are greater than 3/10 but less than 4/5. We can do this by drawing a number line and marking the points:
0 ----------------------|---------------------- 1
3/10 4/5
Lori wants to trade more than 3/10 but less than 4/5 of her stickers, so any point between 3/10 and 4/5 (excluding the endpoints) represents an amount she might trade. For example, she might trade 1/2, 2/3, or 3/4 of her stickers.
To find the fraction of stickers Lori might trade, we can subtract the lower bound from the upper bound:
4/5 - 3/10 = 8/10 - 3/10 = 5/10
Therefore, Lori might trade any fraction between 3/10 and 4/5 (excluding the endpoints), and the fraction of stickers she might trade is 5/10, which simplifies to 1/2.
Step-by-step explanation:
Answer question from the images below Ig..
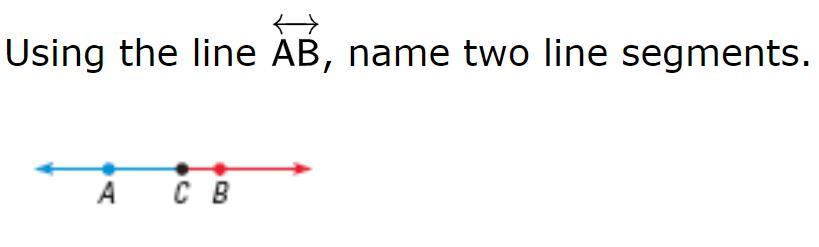
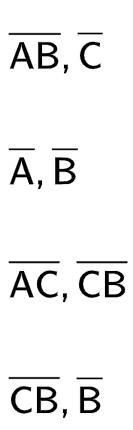
Answers
Answer:
AC, CB
Step-by-step explanation:
A segment needs two endpoints. The third answer is the only one that can contain two segments, other answers contain single points.
One bundle of shingles covers 32 square feet. How many bundles should you buy to cover a roof that is 540 ft2?
Answers
Answer:
17 bundles
Step-by-step explanation:
540 divided by 32 is around 16.875, so buy 17 bundles
Answer:
You should by 17 bundles of shingles.
Step-by-step explanation:
540 divided by 32 is 16.875.
So, you will need almost 17 bundles.
If you were to only buy 16, you would not have enough.
Find the cosine of ZS.
37
S
T T
12
35
R
Simplify your answer and write it as a proper
fraction, improper fraction, or whole number.
COS (S) =
Geometry

Answers
Step-by-step explanation:
cos=adj/hyp cos=12/37=cos-1 0.324=71.09°
Help? Plz! You will be blessed! I need help badly!

Answers
Answer:
819
Step-by-step explanation:
Describe the range of possible distances from the beach to the theater
Answers
The range of possible distances from the beach to the theater is 2 km to 16 km, calculated by subtracting the distance between the theater and the house (7 km) from the distance between the beach and the house (9 km), and adding it back.
To calculate the range of possible distances from the beach to the theater, we can use the information provided
Start with the distance between the beach and the house: 9 km.
Subtract the distance between the theater and the house: 7 km.
9 km - 7 km = 2 km.
This gives us the minimum possible distance from the beach to the theater: 2 km.
Add the distance between the theater and the house: 7 km.
9 km + 7 km = 16 km.
This gives us the maximum possible distance from the beach to the theater: 16 km.
Therefore, the range of possible distances is from 2 km to 16 km.
To know more about distances:
https://brainly.com/question/31713805
#SPJ4
--The given question is incomplete, the complete question is given below " Describe the range of possible distances from the beach to the theater "--

A county reported the following data on breast cancer for the past year. what is the prevalence rate per 100,000? number of new cases: 1,774; number of total cases: 4,192; population: 5,977,906
Answers
The prevalence rate per 100,000 is 99.8%
We know that the prevalence rate is the proportion of persons in a population who have a particular disease over a specified period of time.
In this question, we have been given a data on breast cancer for the past year:
number of new cases: 1,774;
number of total cases: 4,192;
population: 5,977,906
We need to find the prevalence rate per 100,000
The total number of infected people = 1,774 + 4192
= 5966
Chance of infection in the whole population would be,
5,977,906/ 5966 ≈ 1002
This means, chances of having breast cancer is 1 in every 1002 people.
A prevalence rate is calculated by dividing total number of infected people by the total population. The result is then multiplied by 100,000
Now we calculate the prevalence rate per 100,000
= (5966 / 5,977,906) × 100,000
= 0.000998 × 100,000
= 99.8 %
Therefore, the prevalence rate per 100,000 is 99.8%
Learn more about the prevalence rate here:
https://brainly.com/question/14739993
#SPJ4
help meee pleaseee with this problem

Answers
The value of side x in the triangle is 18.1.
What is sine rule?In trigonometry, sine rule is an equation relating the lengths of the sides of any triangle to the sines of its angles.
To find the length of side x in the triangle, we use sine rule formula below.
Formula:
SinA/a = SinB/b..................... Equation 1From the diagram in the question,
Given:
A = 53°a = xB = 180-(95+53) = 32°b = 12Substitute these values into equation 1
sin53°/x = sin32°/12Make x the subject of the equation
x = 12sin53°/sin32°x = 18.1Hence, the value of x is 18.1
Learn more about sine rule here: https://brainly.com/question/28523617
#SPJ1
WILL MARK YOU BRAINLIEST

Answers
Answer:
see in the picture, u can see that JKLM is a parallelogram
=> JK = LM
<=> 3x - 2 = x + 6
<=> 2x = 8
<=> x = 4
with x = 4 => JA = 2.4 - 1 = 7
An object is placed a distance r in front of a wall, where r exactly equals the radius of curvature of a certain concave mirror. At what distance from the wall should this mirror be placed so that a real image of the object is formed on the wall? Express your answer in terms of r. What is the magnification of the image? Follow the sign conventions. Express your answer using three significant figures.
Answers
The concave mirror should be placed at a distance of 2r from the wall to form a real image of the object on the wall. The magnification of the image is expressed using three significant figures is -0.500.
if the object is placed at a distance r in front of a concave mirror whose radius of curvature is also r, then the image is formed at the same distance r behind the mirror. This is a special case called the "center of curvature" configuration.
To form a real image on the wall, the mirror must be placed such that the object is beyond the mirror's focal point. The focal length of the mirror is half of its radius of curvature, so the focal length is f = r/2.
If the object is placed at a distance x from the mirror, then using the mirror equation:
1/f = 1/do + 1/di
where do is the distance of the object from the mirror and di is the distance of the image from the mirror. In this case, do = x and di = r, so we get:
1/r = 1/x - 1/f
Substituting f = r/2, we get:
1/r = 1/x - 2/r
Solving for x, we get:
x = 2r
Therefore, the mirror should be placed at a distance of 2r from the object to form a real image on the wall.
To find the magnification of the image, we use the magnification equation:
m = -di/do
where m is the magnification, di is the distance of the image from the mirror, and do is the distance of the object from the mirror. In this case, do = x = 2r and di = r, so we get:
m = -r/(2r) = -1/2
Therefore, the magnification of the image is -0.500.
Learn more about concave mirrors at
brainly.com/question/31379461
#SPJ4
hallar el angulo complementario sabiendo que uno de ellos es de 35 grados utilizando el metodo de despeje
Answers
Answer:
55°
Step-by-step explanation:
complementario = add to 90°
90°-35°= 55°
What is the central metaphor presented in six degrees of separation?.
Answers
The central metaphor which is presented in six degrees of separation is:
People are much more interconnected than they believeWhat is Metaphor?This refers to the figure of speech which makes use of comparison to show the similarity between two different things.
With this in mind and from the concept of six degrees of separation, we can see that it is based on the theory that people are about six or fewer connections away from each other.
Read more about metaphor here:
https://brainly.com/question/9418370
Given mn, find the value of x.
(5X-4)°
(4x-2)°

Answers
Answer:
x = 2
Step-by-step explanation:
5x - 4 = 4x - 2
So we put 4x to the other side and 4 to the other side to combine them with their like terms.
5x - 4x = 4 - 2
So x = 2
Hope this helps
Find the cp
Wooden shelf : sp = 6786, loss % = 13%
Answers
Answer:
cp=(SP * 100 ) / ( 100 – percentage loss)
6786*100/100-13
7800
Consider the line y = 2x–4.
What is the slope of a line parallel to this line?
What is the slope of a line perpendicular to this line?
Answers
Parallel slope = 2
This is because the original line has slope 2. Parallel lines have equal slopes.
--------------------------
Perpendicular slope = -1/2
The original slope 2 or 2/1 turns into -1/2 after flipping the fraction and the sign. Note the original slope and perpendicular slope multiply to -1. This is true for any pair of perpendicular lines where neither line is vertical.
Answer:
the slope of the parallel line is 2x
the slope of line perpendicular is -1/2
Step-by-step explanation:
In an animal shelter, the ratio of dogs to cats is 5 to 3. There are 25 dogs. Write and solve a proportion to find the number c of cats? I need help ASAP ...
Answers
Answer:
5 = 25
3 = 15
Step-by-step explanation:
25/5 = 5
So, 5 x 5 = 25
3 x c =
Then, 3 x 5 = 15
5 = 25
3 = 15
3. (3 pts) Find the general solution of the following homogeneous differential equations. 2xyy' + (x² - y²) = 0
Answers
The general solution of the given homogeneous differential equation is:y = ±x√(Cx² + 2)
The given differential equation is: 2xyy' + (x² - y²) = 0
We have to find the general solution of the given homogeneous differential equation. To solve the above differential equation, we will use the substitution method.
Put y = vx and y' = v + xv'
Differentiating both sides w.r.t x: y' = v + xv' ⇒ v' = (y' - v)/x
Differentiating again w.r.t x: y'' = v' + xv'' + v' ⇒ y'' = (y'' - 2y'v + v² + xv')/x
Substituting these values in the given differential equation:
2x(v)(v + xv') + (x² - v²x²) = 0
2v + 2x²v' + x - v² = 0
2x²v' + 2v/x - v³/x = -1/x
We can write the above differential equation as:
2x²dv/dx + 2v/x = v³/x - 1/x
Separating the variables and integrating both sides:
∫dx/x = ∫[v/(v² - 2)]dv/x
⇒ ln |x| + ln |v² - 2| + C
⇒ ln |x(v² - 2)| = ln |Cx|
⇒ v² - 2 = Cx² (where C is a constant)
⇒ v = ±√(Cx² + 2)
Putting the value of v in y = vx, we get:
y = x√(Cx² + 2) and y = -x√(Cx² + 2)
To know more about differential equation visit:
https://brainly.com/question/25731911
#SPJ11
A population has a mean of 53 and a standard deviation of 21. A sample of 49 observations will be taken. The probability that the sample mean will be greater than 57.95 is ___. a. 0.450 b. 0.9505 c. 0.0495 d. 0
Answers
The probability that the sample mean will be greater than 57.95 is 0.0495.
What is probability?Probability means possibility. It is a branch of mathematics that deals with the occurrence of a random event. The value is expressed from zero to one. This is the basic probability theory, which is also used in the probability distribution.
To solve this question, we need to know the concepts of the normal probability distribution and of the central limit theorem.
Normal probability distributionProblems of normally distributed samples can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z=\dfrac{X-\mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Central Limit TheoremThe Central Limit Theorem establishes that, for a random variable X, with mean \(\mu\) and standard deviation \(\sigma\), a large sample size can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(\frac{\sigma}{\sqrt{\text{n}} }\).
In this problem, we have that:
\(\mu=53,\sigma=21,\text{n}=49,\text{s}=\frac{21}{\sqrt{49} }=3\)The probability that the sample mean will be greater than 57.95
This is 1 subtracted by the p-value of Z when X = 57.95. So
\(Z=\dfrac{X-\mu}{\sigma}\)
By the Central Limit Theorem
\(Z=\dfrac{X-\mu}{\text{s}}\)
\(Z=\dfrac{57.95-53}{3}\)
\(Z=1.65\)
\(Z=1.65\) has a p-value of 0.9505.
Therefore, the probability that the sample mean will be greater than 57.95 is 1-0.9505 = 0.0495
To know more about the probability visit:
https://brainly.com/question/31321667
let p be a prime number with p ≥ 7. what can you say about whether 2, 5 and 10 are quadratic residues modulo p?
Answers
For a prime number p with p ≥ 7, we can conclude that 2, 5, and 10 are quadratic residues modulo p.
To determine whether 2, 5, and 10 are quadratic residues modulo p, we need to consider the Legendre symbol, denoted as (a/p), which is defined as follows:
(a/p) = 1 if a is a quadratic residue modulo p,
(a/p) = -1 if a is a quadratic non-residue modulo p,
(a/p) = 0 if a ≡ 0 (mod p).
Given that p is a prime number with p ≥ 7, we can examine the Legendre symbols for 2, 5, and 10.
For 2: (2/p) = 1 if p ≡ ±1 (mod 8), and (2/p) = -1 if p ≡ ±3 (mod 8). Since p is a prime number with p ≥ 7, it will fall into either of these categories, making 2 a quadratic residue modulo p.
For 5: (5/p) = 1 if p ≡ ±1, ±4 (mod 5), and (5/p) = -1 if p ≡ ±2, ±3 (mod 5). Again, since p is a prime number with p ≥ 7, it will satisfy one of these conditions, making 5 a quadratic residue modulo p.
For 10: (10/p) = (2/p)(5/p). From the above discussions, we know that both 2 and 5 are quadratic residues modulo p. Therefore, their product 10 is also a quadratic residue modulo p.
In conclusion, for a prime number p with p ≥ 7, we can assert that 2, 5, and 10 are quadratic residues modulo p.
Learn more about prime number here:
https://brainly.com/question/30358834
#SPJ11
Emilio bakes 2 pies. He shares them equally among 3 friends. How much pie does each person get? Express your answer as a fraction
Answers
help please!
Jackie deposited $315 into a bank account that earned 1.5% simple interest each year. No money was deposited into or withdrawn from the account.
How much money was in the account after 3 years?
Answers
Answer:
that is a whole lot of simple intrest
The daily cost of hiring a plumber, y, to work x hours on a repair project can be modeled
using a linear function. The plumber charges a fixed cost of $80 plus an additional cost of
$45 per hour. The plumber works a maximum of 8 hours per day.
For one day of work, what is the range of the function for this situation?
A0
B 80
C 0
D 45 < < 685
Answers
Answer:
i have the same question
Step-by-step explanation:
i have the same question
A fair coin is tossed repeatedly until the first "H" shows up - i.e. the outcome of the experiment is the number of tosses required until the first H occurs (1) What is the sample space for this experiment?(2) Find the probability law for this experiment - i.e. the P(each outcome) [Hint: Use tree diagram representation]
Answers
1) The sample space consists of all possible outcomes of coin tosses until the first "H" occurs
2) Probability of each outcome given by (1/2)^(n+1) where n is the number of tails before the first head
1) How to determine the sample space?The sample space for this experiment is the set of all possible outcomes of the coin tosses until the first "H" occurs. This includes all possible sequences of "T" (tails) and "H" (heads), with the restriction that the first "H" must be the last element in the sequence. For example, some possible outcomes are:
"H" (the first toss is heads)
"TH" (the first heads is on the second toss)
"TTTH" (the first heads is on the fourth toss)
2) How to find the probability law for this experiment?To find the probability law for this experiment, we can use a tree diagram to represent all possible outcomes and their probabilities. At each node in the tree, we branch to represent the two possible outcomes of the next coin toss (heads or tails). The probability of each branch is 1/2, since the coin is fair.
Here is the first level of the tree:
H (probability 1/2)
T (probability 1/2)
If the first toss is heads, we have reached the desired outcome and the experiment ends. If the first toss is tails, we continue branching:
T - H (probability 1/2 * 1/2 = 1/4)
T - T (probability 1/2 * 1/2 = 1/4)
If the second toss is heads, the experiment ends with a total of two tosses. If the second toss is tails, we continue branching:
T - T - H (probability 1/2 * 1/2 * 1/2 = 1/8)
T - T - T (probability 1/2 * 1/2 * 1/2 = 1/8)
We can continue this process to generate the full tree, which has an infinite number of levels (since the experiment could theoretically go on forever). However, we can see that each outcome corresponds to a unique path through the tree, and the probability of that outcome is the product of the probabilities along that path. For example, the outcome "TH" has probability 1/2 * 1/2 = 1/4, while the outcome "TTTH" has probability 1/2 * 1/2 * 1/2 * 1/2 = 1/16.
Therefore, the probability law for this experiment is:
P("H") = 1/2
P("TH") = 1/4
P("TTH") = 1/8
P("TTTH") = 1/16
In general, the probability of the outcome "T^nH" (where there are n tails before the first heads) is (1/2)^{n+1}. The probability of the experiment going on forever (i.e. never getting heads) is 0, since the probability of this outcome is the limit of (1/2)^{n+1} as n approaches infinity, which is 0.
Learn more about probability
brainly.com/question/11234923
#SPJ11
Please Help me With this 30 points and brainliest to first person

Answers
Answer:
(4 * (1 + 2 * 3))^5
Step-by-step explanation:
Try many possibilites and see which one is greater.
The '5' should be an exponent, as it will make the result very large.
Multiplication is usually an operation that makes numbers very big.
Hopefully!!!
State whether the given measurements determine zero, one, or two triangles. A = 58°, a = 25, b = 28
Answers
Answer:
1
Step-by-step explanation:
I believe it is 1. Just picture or draw a diagram of the constraints. Don't quote me on this though...
Answer:
Step-by-step explanation:
apply sine formula
\(\frac{a}{sin ~A} =\frac{b}{sin~B} \\\frac{25}{sin~58} =\frac{28}{sin ~B} \\sin~B=\frac{28}{25} \times sin~58\\B=sin^{-1} (\frac{28}{25} \times sin ~58)=71.77 \approx 72 ^\circ\)
so third angle=180-(58+72)=180-130=50°
∠C=50°
\(cos ~C=\frac{a^2+b^2-c^2}{2ab} \\or ~2abcos~C=a^2+b^2-c^2\\2*25*28*cos ~50=25^2+28^2-c^2\\c^2=625+784-1400 *cos~50\\c^2=1409-899.90\\c^2=509.1\\c=\sqrt{509.1} \approx 22.56 \approx 22.6\)
so one triangle is formed.