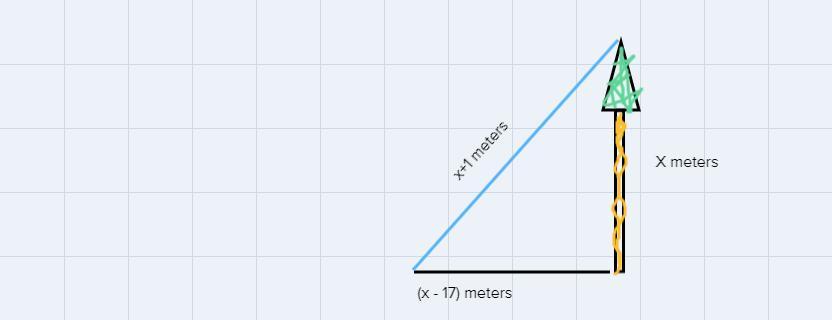
At a certain time of day, a tree that is x meters tall casts a shadow that x - 17 meters long. If the distance from the top of the tree to the end of the shadow is x + 1 meters, what is the height, X_{1} of the tree?

The only true statement about the domain of the given function is:

B. f(x) is negative for all x < -5

The domain of a function is defined as the set of values that we can possibly plug into our function. This set is the x values in a function such as f(x).

Now, we are given the function as:

f(x) = \(\frac{2}{x^{2} } + 3x - 10\)

When x < -5, we have:

f(-4) = \(\frac{2}{(-4)^{2} } + 3(-4) - 10\)

f(-4) = -21.875

This suggests that for all values below x = -5 will result in negative values

When x > 2

f(3) = \(\frac{2}{3^{2} } + 3(3) - 10\)

f(3) = -0.78

Thus, it will get positive for higher values but it can also be negative as seen here.

Read more about Domain of Function at: https://brainly.com/question/10197594

#SPJ1

Answer:

a

The sample size is  \(n = 219.2\)

b

The  sample size is  \(n = 537.5\)

Step-by-step explanation:

From the question we are told  that

    The standard deviation is  \(\sigma = 45 \minutes\)

    The  Margin of  Error is  \(E = \pm 5 \ minutes\)

Generally the margin of  error is mathematically represented as

         \(E = z * \frac{\sigma }{\sqrt{n} }\)

Where  n is the sample  size

    So

             \(n = [\frac{z * \sigma }{E} ]^2\)

Now  at  90%  confidence level the z value for the z-table is  

        z =  1.645

So

       \(n = [\frac{1.645 * 45 }{5} ]^2\)

       \(n = 219.2\)

The z-value at 99%  confidence level is  

        \(z = 2.576\)

This is obtained from the z-table  

   So the sample size is  

         \(n = [\frac{2.576 * 45 }{5} ]^2\)

        \(n = 537.5\)

For the 90% confidence interval, the sample size is 219.2 and for the 99% confidence interval, the sample size is 537.5 and this can be determined by using the formula of margin of error.

Given :

The formula of the margin of error can be used in order to determine the sample size is needed if the executive wants to be 90% confident of being correct to within 5 minutes.

\(\rm ME = z\times \dfrac{\sigma}{\sqrt{n} }\)

For the 90% confidence interval, the value of z is 1.645.

Now, substitute the values of all the known terms in the above formula.

\(\rm n=\left(\dfrac{z\times \sigma}{ME}\right)^2\)   --- (1)

\(\rm n=\left(\dfrac{1.645\times 45}{5}\right)^2\)

n = 219.2

Now, for 99% confidence interval, the value of z is 2.576.

Again, substitute the values of all the known terms in the expression (1).

\(\rm n=\left(\dfrac{2.576\times 45}{5}\right)^2\)

n = 537.5

For more information, refer to the link given below:

https://brainly.com/question/6979326

Answer:

Yes, the ordered pair (1, 2) is a solution to the system.

Step-by-step explanation:

The answer can be found quite quickly. Simply substitute the x coordinate of the given pair for x, and the y coordinate of the given pair for y.

The x coordinate is 1 and the y coordinate is 2, so...

3(1) - 4(2) = -5

2=4(1)-2.

Next, simplify:

3-8=-5

This equation is TRUE.

2=4-2

This equation is also TRUE.

Hopefully, this helps in some way!

Answer:

-0.5

Step-by-step explanation:

σM=σ/√N

=9/√36

=9/6

=3/2=1.5

Z=(x-μ)/σ/√N

=(19.5-24)/9/√36

=-4.5/1.5=-3

The probability that the sample mean will be larger than 19.5 = -0.5

P(>19.5)=P(Z>-3)= -0.5

Answer:

80 + 30h

Step-by-step explanation:

(10 * 8) + (10 * 3h)

=80 + 30h

\(\Large\boxed{\tt Anwer:~80+30h}\)

\(\tt Step-by-step~explanation:\)

We need to distribute the 10 to 8 and 3h. In order to do this, we can multiply 10 by 8 and 10 by 3h.

\(\tt 10*8=80\\10*3h=30h\)

Then, we add them together to get the answer.

\(\tt 80+30h\)

Answer:

66

Step-by-step explanation:

dolars per hour

Answer:

$9

Step-by-step explanation:

DELTAMATH

Answer:

Proportional relationships are relationships between two variables where their ratios are equivalent. Another way to think about them is that, in a proportional relationship, one variable is always a constant value times the other. That constant is know as the "constant of proportionality"

Step-by-step explanation:

I learned it.

Answer:

\( P \geq 1000 \; meters \)

Step-by-step explanation:

Given the following data;

Length = 312 meters

Breadth = 186 meters

To find the perimeter of the rectangle;

Mathematically, the perimeter of a rectangle is given by the formula;

Perimeter = 2(L + W)

Perimeter = 2(312 + 186)

Perimeter = 2(498)

Perimeter = 996 meters

To the nearest meters, we have;

Perimeter = 996 ≈ 1000 meters

Let P represent the perimeter of a rectangular field.

900 < P > 1000

Therefore, \( P \geq 1000 \; meters\)

Answer:

The points (0, 3) and (0, 1) are located on the same axis.

Step-by-step explanation:

coordinates are in the format (x, y) where x is how far it is on the x axis and y is how far it is on the y axis.

x axis is the horizontal (left and right)

y axis is the vertical (up and down)

Using cosine function:

Answer:

x = 11.31

Answer:

g(x)=(1/3x)² .................

Answer:

\(\frac{1}{240} = 0.0042\) = 0.42% probability that the first 2 presentations will be by Drake and Todd, in that order.

Step-by-step explanation:

A probability is the number of desired outcomes divided by the number of total outcomes.

In this question, since the order in which the students are chosen is important, the permutations formula is used to solve it.

Permutations formula:

The number of possible permutations of x elements from a set of n elements is given by the following formula:

\(P_{(n,x)} = \frac{n!}{(n-x)!}\)

Desired outcomes:

Drake then Todd, so only one outcome, which means that \(D = 1\)

Total outcomes:

Two students from a set of 16, so:

\(T = P_{16,2} = \frac{16!}{14!} = 16*15 = 240\)

What is the probability that the first 2 presentations will be by Drake and Todd, in that order?

\(p = \frac{D}{T} = \frac{1}{240} = 0.0042\)

\(\frac{1}{240} = 0.0042\) = 0.42% probability that the first 2 presentations will be by Drake and Todd, in that order.

The probability that a randomly selected person from this sample was a friend of the bride OR of the groom is 0.9875.

Given that, at a wedding each guest asked the 80 guests whether they were a friend of the bride or of the groom.

What is the probability?

Probability can be defined as the ratio of the number of favorable outcomes to the total number of outcomes of an event.

Total Number of Guests which forms the Sample Space, n(S)=80

Let the event (a friend of the bride) =A

Let the event (a friend of the groom) =B

n(A) =59

n(B)=50

Friends of both bride and groom,

So,

n(A∪B)=n(A)+n(B)-n(A∩B)

n(A∪B)=59+50-30

n(A∪B)=79

The number of Guests who was a friend of the bride OR of the groom = 79

Thus,

P(A∪B)=n(A∩B)/n(S)

= 79/80

= 0.9875

Hence, the probability that a randomly selected person from this sample was a friend of the bride OR of the groom is 0.9875.

To learn more about the probability visit:

brainly.com/question/11234923.

#SPJ4

Answer:

4,-2 1/2 is the coordinates of point F.as it

lies in 4 th quadrant where x is positive and y is negative.

Chandler ended up 8 feet below sea level. The negative sign indicates that his final position is below sea level. This means that he has descended further into the lake compared to the starting point on the cliff.

Chandler started on the cliff at 32 feet above sea level. When he jumped for 40 feet, we need to determine the final position in relation to sea level.

Since Chandler jumped down, the distance below sea level will be calculated as a negative value. To find how far below sea level Chandler ended up, we subtract the jump distance (40 feet) from the starting height (32 feet above sea level):

32 feet - 40 feet = -8 feet

It's important to note that negative values are used here to represent the direction and magnitude of Chandler's descent relative to sea level

For more such questions on feet

https://brainly.com/question/30403118

#SPJ8

Answer:

-8 feet

Step-by-step explanation:

Answer:

4y

Step-by-step explanation:

Answer:

perimeter=4y

Step-by-step explanation:

y+y+y+y=4y

..........

Answer:

1500kg

Step-by-step explanation:

50*30=1500

Answer:

1. (a)  [-1, ∞)

   (b)  (-∞, -1) ∪ (1, ∞)

2. (a)  (1, 3)

    (b)  (-∞, 1) ∪ (3, ∞)

3. (a)  9.6 m and 0.4 m

   (b)  03:08 and 15:42

Step-by-step explanation:

The domain of a function is the set of all possible input values (x-values).

The range of a function is the set of all possible output values (y-values).

Part (a)

When x < 0, the function is f(x) = x².

Since the square of any non-zero real number is always positive, the range of the function f(x) for x < 0 is (0, ∞).

When x ≥ 0, the function is f(x) = sin(x).

The minimum value of the sine function is -1 and the maximum value of the sine function is 1.  As the sine function is periodic, the function oscillates between these values.  Therefore, the range of function f(x) for x ≥ 0 is [-1, 1].

The range of function f(x) is the union of the ranges of the two separate parts of the function.  Therefore, the range of f(x) is [-1, ∞).

Part (b)

The domain of the function g(x) = ln(x² - 1) is the set of all real numbers x for which (x² - 1) is positive, since the natural logarithm function (ln) is only defined for positive input values.

Find the values of x:

\(\implies x^2-1 > 0\)

\(\implies x^2 > 1\)

\(\implies x < -1, \;\;x > 1\)

Therefore, the domain of function g(x) is (-∞, -1) ∪ (1, ∞).

Part (a)

To determine the interval where f(x) < 0, we need to find the values of x for which the quadratic is less than zero.

First, set the function equal to zero and solve for x:

\(\begin{aligned} x^2-4x+3&=0\\x^2-3x-x+3&=0\\x(x-3)-1(x-3)&=0\\(x-1)(x-3)&=0\\ \implies x&=1,\;3\end{aligned}\)

Therefore, the function is equal to zero at x = 1 and x = 3 and so the parabola crosses the x-axis at x = 1 and x = 3.

As the leading coefficient of the quadratic is positive, the parabola opens upwards. Therefore, the values of x that make the function negative are between the zeros.  So the interval where f(x) < 0 is 1 < x < 3 = (1, 3).

Part (b)
Since the square root of a negative number cannot be taken, and dividing a number by zero is undefined, function f(x) has to be positive and not equal to zero:  f(x) > 0.

As the parabola opens upwards, the values of x that make the function positive are less than the zero at x = 1 and more than the zero at x = 3.

Therefore the domain of g(x) is (-∞, 1) ∪ (3, ∞).

Part (a)

The range of a sine function is [-1, 1]. Therefore, to calculate the maximal and minimal possible water depths of the bay, substitute the maximum and minimum values of sin(t/2) into the equation:

\(\textsf{Maximum}: \quad 5+4.6(1)=9.6\; \sf m\)

\(\textsf{Maximum}: \quad 5+4.6(-1)=0.4\; \sf m\)

Part (b)

To find the times when the depth is maximal, set sin(t/2) to 1 and solve for t:

\(\implies \sin \left(\dfrac{t}{2}\right)=1\)

\(\implies \dfrac{t}{2}=\dfrac{\pi}{2}+2\pi n\)

\(\implies t=\pi+4\pi n\)

Therefore, the values of t in the interval 0 ≤ t ≤ 24 are:

Convert these values to times:

Answer:  6x² + 11

Step-by-step explanation:

  24x³ - 54x²    +    44x - 99

=  6x²(4x - 9)     +    11(4x - 9)

=  (6x² + 11) (4x - 9)

This can be rewritten as: 4x(6x² + 11) - 9(6x² + 11)

This is the answer to your problem.

The function that models each variation is a) y = 100/x. When x = 10: y = 100/10 = 10. b) y = -80/x. When x = 10: y = -80/10 = -8.

When one variable rises, the other one falls, and vice versa, two variables are negatively correlated. This indicates that the two variables' product has a fixed value. In other words, we may express the relationship between two inversely varying variables, x and y, as follows:

xy = k

where k is a proportionality constant. To maintain the same value of the product when one variable rises, the other must fall. Inverse variation examples include the link between the amount of time required to go a certain distance at a constant pace or the amount of workers required to finish a task in a certain amount of time.

If y varies inversely with x, we can write the relationship as:

y = k/x

a) When x = 20 and y = 5:

5 = k/20

k = 100

Substituting k we have:

y = 100/x

When x = 10:

y = 100/10 = 10

b) When x = 20 and y = -4:

-4 = k/20

k = -80

Substituting k we have:

y = -80/x

When x = 10:

y = -80/10 = -8

Learn more about inverse proportions here:

https://brainly.com/question/2548537

#SPJ1

The equation that produces the circle in the given graph is; x² + y² = 16

The general form of equation of a circle is;

(x - h)² + (y - k)² = r²

where;

h, k are coordinates of the circle center

r is the radius

From the graph, we can see that the coordinates of the center is; (0, 0).

Also, radius is;

r = √(4² - 0²)

r = √16

Thus, our equation of the circle in the graph is;

(x - 0)² + (y - 0)² = (√16)²

⇒ x² + y² = 16

Read more about Circle Equation at; https://brainly.com/question/1559324

#SPJ1

Answer:

x^2/20+y^2/20=1 is the correct answer.

Step-by-step explanation:

Answer:

Here it goes -0.333

Answer:

4.62%

Step-by-Step Explanation:

Ask yourself: "3 is what percent of 65?" and solve.

Percentage solution with steps:

Step 1: We make the assumption that 65 is 100% since it is our output value.

Step 2: We next represent the value we seek with x.

Step 3: From step 1, it follows that 100%=65.

Step 4: In the same vein, x%=3.

Step 5: This gives us a pair of simple equations:

100%=65(1)

x%=3(2)

Step 6: By simply dividing equation 1 by equation 2 and taking note of the fact that both the LHS

(left hand side) of both equations have the same unit (%); we have

100% / x% =65 / 3

Step 7: Taking the inverse (or reciprocal) of both sides yields

x% / 100% =3 / 65

---> x = 4.62%

Therefore, 3 is 4.62% of 65.

Answer:

2/3 pounds of lima beans

Step-by-step explanation:

2 divided by 3 = 2/3 = 2/3

Hope this helps!

Answer:

2/3 pounds (Option B)

Step-by-step explanation:

Using unitary method ,

3 families will receive = 2 pounds of lima beans.

(Dividing both the sides by 3)

⇒ \(\frac{3}{3}\)  family will receive = \(\frac{2}{3}\) pounds of lima beans

⇒ 1 family will receive = \(\frac{2}{3}\) pounds of lima beans.

∴ Each family will receive 2/3 pounds of lima beans.

Answer:

its 1

Step-by-step explanation:

Answer:

Step-by-step explanation:

183,883,72

Answer:

18388372

Step-by-step explanation:

1 )Use the algorithm method.

      3 2 1 7

×              5      7      1      6

        1      1       1      4                      

        1      9      3      0     2            

        3 2  1  7 0

  2 1  1     4  

  2 2 5    1       9      0     0

1  1     3

1  6 0 8   5       0      0     0

      1  1    1

1  8 3 8   8       3       7     2

2 )Therefore, 3217 × 5716 = 18388372.

18388372

Answer:

B.

you actually just have to look for the one that says is being multiplied for me thats the easiest way. In this case its 2 thats being multiplied so you just had to look for the one that says that. 2 times means 2x which fits with the problem they are giving you.