At a carnival, Jenny bought 7 packs of 13 tickets each. She has used 39 of the tickets so far. How many tickets does she have left?
Answers
Answer:
52 tickets
Step-by-step explanation:
7 x 13 = 91
91 - 39 = 52
Related Questions
Find the
28th term of
3,11, 19, 27
Answers
The 28th term of the given arithmetic sequence is 219
any arithmetic sequence can be solved once we identify the aa1 term and the an term because then we have to simply find the common difference and solve further by substituting the value in the below mentioned equation.
Given the arithmetic sequence = 3,11, 19, 27
a₁ = 3
a₂ = 11
a₃ = 19
a₄ = 27
the common difference or d = a₂ - a₁
this implies d = 11 - 3 = 8
Therefore the 28th term of the given arithmetic sequence is
a₂₈ = a₁ + ( n - 1 ) d
a₂₈ = 3 + ( 28 - 1 ) 8
= 3 + 27 × 8
= 3 + 216
= 219
Thus a₂₈ = 219
To know more about arithmetic sequence visit;
https://brainly.com/question/10396151
#SPJ13
You can use the notation P(A), read “the probability of event B, given event A” to write a
A. Probability distribution
B. Frequency table
C. Conditional probability
D. Cumulative probability
Answers
You can use the notation P(A), read “the probability of event B, given event A” to write a conditional probability. The correct answer is C.
Conditional probability refers to the probability of one event occurring given that another event has already occurred. In this case, we are interested in the probability of event B occurring given that event A has already occurred, and we can represent this using the notation P(B|A), where '|' means 'given'.
For example, let's say we are interested in the probability of getting a head on a coin toss (event B), given that the coin was flipped and landed on heads (event A). We could represent this using the notation P(B|A). The value of P(B|A) would be 1, because if the coin already landed on heads, then the probability of getting a head on the next flip is certain.
Conditional probability is an important concept in probability theory and is often used in real-world applications, such as predicting the likelihood of a disease given certain symptoms, or the probability of an event occurring given certain conditions.
The correct answer is C.
To learn more about probability click on,
https://brainly.com/question/29259732
#SPJ1
Suppose that the salaries, in thousands of dollars, of the managers for a industry are normally distributed with an unknown mean and standard deviation. The salaries of 26 randomly sampled managers are used to estimate the mean of the population. What t-score should be used to find the 95% confidence interval for the population mean
Answers
Answer: t _(α/2) = 2.060
Step-by-step explanation:
Given that;
sample size n = 26
confidence interval = 95%
level of significance α = ( 1 - 95/100 ) = 0.05
but from the question the salaries (26) are use to estimate the mean of the population so, its a two tail test
therefore our level if significance α will be divided by 2 = 0.05/2 = 0.025
now our degree of freedom df = 26 - 1 = 25
FROM standard t-table value
the critical value of t for the level of significance 0.025
and 25 degree of freedom is 2.060
therefore, t _(α/2) = 2.060
What are the steps to solving the inequality 3b + 8 ≥ 14?
Subtract 8 from both sides of the inequality. Divide both sides of the inequality by 3.
Subtract 8 from both sides of the inequality. Change the direction of the inequality. Divide both sides of the inequality by 3.
Divide both sides of the inequality by 3. Subtract 8 from both sides of the inequality.
Divide both sides of the inequality by 3. Change the direction of the inequality. Subtract 8 from both sides of the inequality.
Answers
Answer:Subtract 8 from both sides of the inequality. Divide both sides of the inequality by 3-- A
Step-by-step explanation:
Step 1
In solving 3b + 8 ≥ 14
we first subtract both sides by 8, which will give
3b+ 8 -8 ≥ 14-8
3b ≥ 6
Step 2
Then, divide both sides by 3----Since we are multiplying by a positive number, 3, the inequalities sign will not change but will still remain the same.
3b/3 ≥ 6/3
To give answer as b ≥ 2.
Answer:
A
Step-by-step explanation:
Simplify:
2
(
3
x
)
+
(
x
+
10
)
2(3x)+(x+10)
Answers
Answer:
7x+10
Step-by-step explanation:
2x(3x)+1x(x+10)
6x+1x+10
7x+10
The water depth of a pond is initially 36 inches and decreases at a rate of 0.2 inches per day through evaporation. Write a linear function that represents the depth of the pond at a given time.
Answers
Answer:
36-0.2d
Step-by-step explanation:
d refers to the number of days
This should work for your question if not I'm very sorry
The required expression for the decreasing depth of the pond is y = 36 - 0.2x, Where y is the depth of the pond after x days.
The equation is the relationship between variables and constants represented as y = ax + b is an example of a polynomial equation.
Here,
The water depth of a pond is initially 36 inches
The water depth of a pond decreases at a rate of 0.2 inches per day through evaporation.
Let the number of the days be x , and the depth left be y
According to the question,
Total depth in x days = 0.2x
Total remaining depth = 36 - 0.2x
or
y = 36 - 0.2x
Thus, the required expression for the decreasing depth of the pond is y = 36 - 0.2x, Where y is the depth of the pond after x days.
Learn more about equations here:
brainly.com/question/10413253
#SPJ5
The unshaded regions are quarter circles. Which choice best approximates the area of the shaded region? Use ≈3.14. 24
Answers
Answer:
The probability that a point chosen at random will be in the shaded region is 0.25
Step-by-step explanation:
We have been given a small shaded circle inside a larger un-shaded circle. This is shown in the image attached below.
The area of smaller circle is 78.5 squares inches and the area of larger circle is 314 square inches. We have to find the probability that a point chosen at random will be in the shaded region.
Probability is defined as the ratio of Favorable outcome to the Total outcomes. In this case the favorable outcome is that the point should be inside the shaded region i.e. in an Area of 78.5 square inches. And the total outcome is that the point can be anywhere inside the larger circle i.e. within an Area of 314 square inches. Thus the probability that a point chosen at random will be inside the shaded region will be:
\(Probability =favorable-Outcome/total outcome\)
\(=78.5/314\)
\(=0.25\)
Thus, the the probability that a point chosen at random will be in the shaded region is 0.25. This means there is a 25% chance that a randomly chosen point will be inside the shaded region.
Given 3 + 7 + 11 + 15 + … find S20
Answers
Answer:
Hi
Please mark brainliest ❣️
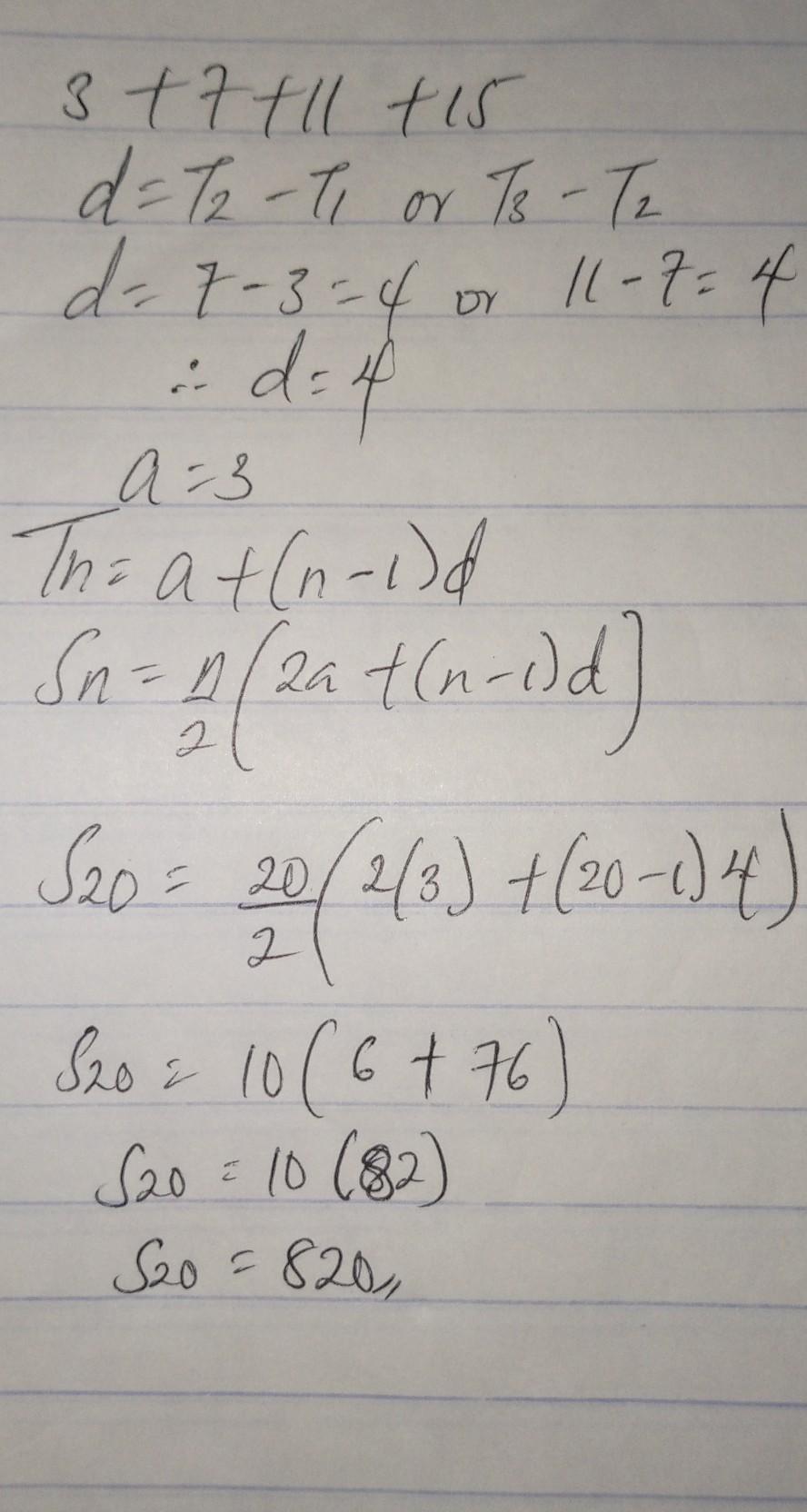
Simplify the expression

Answers
Answer:
5 3^/2x^3
Step-by-step explanation:
Lauren build a sandbox shaped like an octagon each side of the sandbox is the same like the perimeter of the sandbox is 18.8 ft how long is each side of the sandbox
Answers
Answer:
Step-by-step explanation:
Answer:
6ft
Step-by-step explanation:
oof oof oof oof oof oof oof oof oof oof oof oof oof oof oof
Please help answer my question

Answers
Answer:
x = 6
Step-by-step explanation:
This is a bit of a tricky equation, and it's what we call an exponential equation since it involves some exponents. The way we begin to solve these kinds of problems is make the base on each side of the equals sign the same. On one side, we have 9 as our base, and on the other side, we have 3 as our base. 9 = 3², so we can rewrite our equation as shown below:
(3²)⁴ˣ⁻¹⁰ = 3⁵ˣ⁻²
From there, we can use the exponent rule (xᵃ)ᵇ = xᵃᵇ to simplify the left side of the equation.
3²⁽⁴ˣ⁻¹⁰⁾ = 3⁵ˣ⁻²
3⁸ˣ⁻²⁰ = 3⁵ˣ⁻²
Since our bases are now the same, we can take just the exponents and turn it into a new equation as shown below:
8x - 20 = 5x - 2
Hopefully at this point, this problem becomes easy for you, but I'll show how I solved this new equation below in case it doesn't make sense.
8x - 20 = 5x - 2
8x - 20 - 5x = 5x - 2 - 5x
3x - 20 = -2
3x - 20 + 20 = -2 + 20
3x = 18
3x/3 = 18/3
x = 6
Hopefully that's helpful! Let me know if you need more help. :)
Answer this equation 3(2-4d)-9dx43((2+4-34.2
please answer incorrectly
Answers
Answer:
12+ 23734.9d That's the incorrect answer.
How many tiles can fit in a rectangular floor with length 14 ft and width 6 ft if the the square tiles has an edge of 3/4 ft.
Answers
A rectangular floor with a length of 14 ft and a width of 6 ft, square tiles with an edge length of 3/4 ft, a total of 144 tiles can fit.
To determine how many square tiles can fit in a rectangular floor, we need to calculate the total number of tiles that can fit both horizontally and vertically.
Given:
Length of the rectangular floor = 14 ft
Width of the rectangular floor = 6 ft
Edge length of square tile = 3/4 ft
First, let's calculate the number of tiles that can fit horizontally:
Length of the rectangular floor / Edge length of square tile = 14 ft / (3/4 ft) = 14 ft × (4/3 ft) = 56/3 ft
Since we want a whole number of tiles, we need to round down or take the floor value:
Number of tiles horizontally = floor(56/3) = 18 tiles
Next, let's calculate the number of tiles that can fit vertically:
Width of the rectangular floor / Edge length of square tile = 6 ft / (3/4 ft) = 6 ft × (4/3 ft) = 24/3 ft
Again, we round down or take the floor value:
Number of tiles vertically = floor(24/3) = 8 tiles
To find the total number of tiles, we multiply the number of tiles horizontally by the number of tiles vertically:
Total number of tiles = Number of tiles horizontally × Number of tiles vertically = 18 tiles × 8 tiles = 144 tiles
Therefore, in a rectangular floor with a length of 14 ft and a width of 6 ft, square tiles with an edge length of 3/4 ft, a total of 144 tiles can fit.
for such more question on length
https://brainly.com/question/20339811
#SPJ8
If you can help with the explanation I will mark brainpower

Answers
Answer:
It is 90º
Step-by-step explanation:
Looking at the picture, we realize that the angle direcly beside it, EGD, is 90º. Now, both angles form a straight line, which equals 180º. 180-90= 90º.
Answer: A 40 B 50 C 90 D 130
where they go: B goes under A, D goes under the whole thing, just like E (although that doesn't want to be answered) and C goes under B
hope this helped
From the given equation
a) Copy and complete the table
b) Draw the graph of the given equation
c) Find the coordinates of y-intercep

Answers
Answer:
See attacheda)
The table:
x | -3 | -2 | -1 | 0 | 1 | 2 | 3y | -5 | -3 | -1 | 1 | 3 | 5 | 7b)
The graph is picturedc)
The y-intercept has coordinates of (0, 1)
2. Explain how to calculate 8% of 350 by first calculating 1% of 350. PLEASE HELP ASAP
Answers
Answer:
Step-by-step explanation:
To calculate 8% of 350, we can first calculate 1% of 350 and then multiply it by 8.
1% of 350 is equal to 0.01 times 350 which can be calculated as:
0.01 * 350 = 3.5
Since 1% of 350 is equal to 3.5, 8% of 350 can be calculated as follows:
8 * 3.5 = 28
So, 8% of 350 is equal to 28.
Graph the system of inequalities:
-x + 2y - 4 <0
3x + 4y + 420

Answers
Step-by-step explanation:
draw the graph then use the graph to answer the following questions
2. The mean temperature in an area is 74 degrees Fahrenheit. The sum of the temperatures is
2,516. How many temperatures are in the set?
Answers
To find the number of temperatures in the set, we can divide the sum of the temperatures by the mean temperature.
Number of temperatures = Sum of temperatures / Mean temperature
In this case, the sum of temperatures is given as 2,516 and the mean temperature is given as 74 degrees Fahrenheit.
Number of temperatures = 2,516 / 74
Calculating the division:
Number of temperatures ≈ 34.05
Since we cannot have a fraction of a temperature, we need to round the result to the nearest whole number. Therefore, there are approximately 34 temperatures in the set.
Savannah earned a score of 720 on Exam A that had a mean of 700 and a standarddeviation of 25. She is about to take Exam B that has a mean of 400 and a standarddeviation of 100. How well must Savannah score on Exam B in order to doequivalently well as she did on Exam A? Assume that scores on each exam arenormally distributed.
Answers
Answer:
480
Explanation:
First, we need to standardize the score on Exam A. It can standardize as
\(z=\frac{\text{ score}-\text{ mean}}{\text{ standard deviation}}\)Replacing score = 720, mean = 700, and standard deviation = 25, we get
\(z=\frac{720-700}{25}=\frac{20}{25}=0.8\)Then, to do equivalently well on exam B, we need a standard value equal to 0.8. So, the score can be calculated as
\(\text{ score = z\lparen standard deviation\rparen + mean}\)Replacing z = 0.8, standard deviation = 100 and mean = 400, we get
\(\begin{gathered} \text{ score = 0.8\lparen100\rparen+400} \\ \text{ score = 80 + 400} \\ \text{ score = 480} \end{gathered}\)Therefore, the answer is 480
14 points! PLEASE HELP!!!

Answers
Step-by-step explanation:
I just did in the other posting. how often did you post it ?
this is a trick question. the triangle at the top is not an isoceles triangle.
we use Pythagoras for an the steps.
so, the left part of the baseline (split by the height) is calculated by
12² = 10² + part²
144 = 100 + part²
part = sqrt(44) = 6.633249581... ft
the other part is then
20 - 6.633249581... = 13.36675042... ft
and the second leg of the large triangle is
leg² = 10² + 13.36675042...² = 278.6700168...
leg = 16.69341238... ft
P = 12 + 16.69341238... + 8 + 8 + 20 = 64.69341238... ft ≈
≈ 64.69 ft
please see the answer to the other posting for more details.
help!
Can you please give me the area of this. I would really like it.

Answers
Answer:
The answer is 340 ft²
To find the total area we make two squares and a big rectangle.
1st square
3x5=15
2nd square
5x5=25
Rectangle
20x15=300
Total Area
15+25+300 = 340ft²

5 TANE BİLEŞİK KESİR VE 5 TANE BASİT KESİR:Acil!!
Answers
Answer:
çoook yardım etmek isterdim ama biz kesirlerde bu konuyu daha işlemedik çok özür dilerim
Given the two functions, which statement is true?
f(x) = ex, g(x) = ex-2
g(x) is translated down 2 units compared to f(x)
g(x) is translated right 2 units compared to f(x)
g(x) is translated left 2 units compared to f(x)
g(x) is translated up 2 units compared to f(x)
Answers
The function g(x) is translated down 2 units compared to f(x).
Vertical Shift in a Parabola:A vertical shift is a transformation of a parabolic function that moves the entire graph vertically either upwards or downwards.
If the parameter c in the equation of the parabola is increased or decreased by a constant k, the parabola will be shifted vertically by k units.
If k is positive, the parabola will be shifted upward, while if k is negative, the parabola will be shifted downward.
Here we have
Two fuctions f(x) = eˣ, and g(x) = eˣ - 2
Here the function is transformed by subtracting -2
Therefore,
The function g(x) is translated down 2 units compared to f(x).
Learn more about Parabola at
https://brainly.com/question/28079077
#SPJ1
Angles in a Triangle

Answers
Answer:
a = 40°
Step-by-step explanation:
An isosceles triangle has two sides that are the same size. The angles opposite from those sides are equal (they are called base angles.) And, the three angles in a triangle add up to 180°
So,
100 + a + a = 180
combine like terms
100 + 2a = 180
subtract 100
2a = 80
divide by 2
a = 40
given f(x)=3/x and g(x)=x^2-5 find f(g(x))
Answers
To perform the composition, we need to substitute g(x) for x in f(x).
f(g(x)) = 3/(x^2 - 5)
Help 50 points (show ur work)



Answers
1. The value of 34% of 850 is 289.
3. The amount that Kepley paid for the tool is $120.
How to calculate the value?From the information, we want to calculate 34% of 850. This will be calculated thus:
= 34% ×850
= 34/100 × 850
= 0.34 × 850
= 289
The amount paid for the tool will be:
= Price or tool - Discount
= $200 - (40% × $200)
= $200 - $80
= $120
Learn more about percentages on:
brainly.com/question/24304697
#SPJ1
Graph the circle (x-2)^2 + (y-7)^2 = 4
Answers
Answer:
see attached
Step-by-step explanation:
You want the graph of the circle defined by the equation ...
(x-2)^2 + (y-7)^2 = 4.
Circle equationThe equation of a circle with center (h, k) and radius r is ...
(x -h)² +(y -k)² = r²
Comparing this to the given equation, we see ...
h = 2, k = 7, r² = 4
Then r = √4 = 2.
The circle will have its center at (2, 7) and will have a radius of 2. It is shown in the attached graph.
<95141404393>

Write the equation of the line that is parallel to the line 5x- 4y = 4 and passes through one point (-8, 2).
Answers
Answer:
y = 5/4x - 8
Step-by-step explanation:
first you convert the equation to y = mx + b
then you add the the -8 into the x and the 2 into the y and solve for b
b = -8 and since it is parallel same slope.
hope this helps :)
Equation A is equal to (C + D) x (C + D). Equation B is equal to 2 x (C + D). If C and D were numbers that were greater than zero, which equation would give you a bigger value ? Equation A or Equation B ? Give an example for C and D that supports your answer. PLEASE HELP TIMED EXAM!!!!!
Answers
According to the question an example of C = 3 and D = 2 supports the answer that Equation A gives a bigger value than Equation B.
What is equation?Two equations are considered to be comparable when their roots and solutions line up. To create an equivalent equation, the identical quantity, symbol, or expression has to be added to or removed from both of the equation's two sides. We can also create a similar equation by dividing or multiplying each component of an equation with a nonzero value.
given,
To determine which equation would give a bigger value, we can compare the expressions obtained by expanding Equation A and simplifying Equation B.
Expanding Equation A, we get:
A = (C + D) x (C + D) = C² + 2CD + D²
Simplifying Equation B, we get:
B = 2 x (C + D) = 2C + 2D
To compare the values of A and B, let's choose some values for C and D that are greater than zero. Let's choose C = 3 and D = 2.
Plugging these values into Equation A, we get:
A = 3² + 2(3)(2) + 2² = 9 + 12 + 4 = 25
Plugging these values into Equation B, we get:
B = 2(3 + 2) = 2(5) = 10
Since A is greater than B for the values of C = 3 and D = 2, we can conclude that Equation A gives a bigger value than Equation B for positive values of C and D.
Therefore, an example of C = 3 and D = 2 supports the answer that Equation A gives a bigger value than Equation B.
To know more about equation visit:
brainly.com/question/2972832
#SPJ1
Please helppp.
:))
in the photo

Answers
Answer:
0
Step-by-step explanation:
plug each one in. 330 + 0.3= 3.3 + 0.3. that def isnt true, so try 0. thats true since anything x 0 is 0. so, 0. this is so hard tho, so im not 100%