Assume that the heights of men are normally distributed with a mean of 70.9 inches and a standard deviation of 2.1 inches. If 36 men are randomly selected, find the probability that they have a mean height greater than 71.9 inches. Round to four decimal places.
Answers
Answer:
The probability that they have a mean height greater than 71.9 inches
P( x⁻ ≥71.9) = 0.0022
Step-by-step explanation:
Explanation:-
Given mean of the Population μ= 70.9
Standard deviation of the Populationσ = 2.1
Given sample size 'n' =36
let x⁻ be the mean height
given x⁻ =71.9 inches
\(Z=\frac{x^{-} -mean}{\frac{S.D}{\sqrt{n} } }\)
\(Z=\frac{71.9 -70.9}{\frac{2.1}{\sqrt{36} } } = \frac{1}{0.35} = 2.85\)
The probability that they have a mean height greater than 71.9 inches
P( x⁻ ≥71.9) = P(Z ≥ 2.85)
= 1 - P(Z≤ 2.85)
= 1 - ( 0.5 + A(2.85)
= 0.5 - A( 2.85)
= 0.5 - 0.4978
= 0.0022
The probability that they have a mean height greater than 71.9 inches
P( x⁻ ≥71.9) = 0.0022
Answer:
the answer is 0.0022
Step-by-step explanation:
Related Questions
Points g,h,and I are collinear and h is in between g and I. GH=12 and GI=23, what is HI?
Answers
A recipe requires for ⅜ cups of sugar for each cup of flour used. If a baker uses 6 cups of flour, what is the total amount of sugar that will be needed? Show your work. (4.NE.4),
Answers
Answer:
3 cuuuuuuuuuuuuuupsssssss offfccccdd saaaaaaaallllytttt
write the standard equation of a circle with centre (-15;12) and a circumference of 8π
Answers
A circle with center (-15,12) and a circumference of 8π, the standard equation of the circle is (x + 15)² + (y - 12)² = 16.
Explain Standard Equation?A standard equation is a mathematical expression that describes a relationship between two or more variables. It is a specific form of an equation that is commonly used in mathematics, science, and engineering.
In general, a standard equation has the following form:
Ax + By + C = 0
where A, B, and C are constants, and x and y are variables. This equation is called the standard form of a linear equation in two variables.
The standard equation can also be written in other forms, such as slope-intercept form, point-slope form, and general form. Each form of the equation provides different information about the relationship between the variables.
The standard equation of a circle with center (h, k) and radius r is given by:
(x - h)² + (y - k)² = r²
We know that the center of the circle is (-15, 12) and the circumference is 8π. We can use the formula for the circumference of a circle to find the radius:
C = 2πr
8π = 2πr
r = 4
Substituting these values in the standard equation, we get:
(x - (-15))² + (y - 12)² = 4²
(x + 15)² + (y - 12)² = 16
Therefore, the standard equation of the circle is (x + 15)² + (y - 12)² = 16.
To know more about circumference visit:
https://brainly.com/question/17148063
#SPJ1
DUE IN 10 MINS HELP AS SOON AS POSSIBLE ASAP ILL GIVE BRAINLIEST!!

Answers
Answer:
m = -3
Step-by-step explanation:
First, find two clear points:
(1, -2) (0, 1)
Then, use the slope formula:
m = y2 - y1
x2 - x1
m = 1 - (-2)
0 - 1
= 3 = -3
-1
m = -3
This means that the rise-over-run is -3 over 1, or 3 over -1.
Which means three down and 1 to the right, or 3 up and 1 to the left.
Slope is the steepness of the line.
Solve for x - PLEASE NEED HELP, this is my 3rd time posting it.

Answers
Answer:
\(x=58\)
Step-by-step explanation:
First, remember that the maximum degree of an angle totals 360°.
Since we already have 294°, this means that what is left must total \(360\textdegree - 294\textdegree= 66\textdegree\).
Therefore, this means that our two smaller angles must equal 66°. So:
\((36)+(x-28)=66\)
Solve for x. Add on the left:
\(x+8=66\)
Subtract 8 from both sides. Therefore, the value of x is:
\(x=58\)
What is the constant in 12r + r/2-19
Answers
Answer:
constant is - 19
Step-by-step explanation:
the constant is the term in an expression with no variable attached to it.
12r + \(\frac{r}{2}\) - 19
the only term without the variable r attached to it is - 19
then the constant term is - 19
6TH GRADE MATH SOMEONE PLEASE GIVE ANSWER TYSM

Answers
The surface area of the vase is 168.4 square inches.
What is a cylinder?
A cylinder is a three-dimensional geometric shape that has two congruent circular bases connected by a curved surface.
The surface area of the cylindrical vase can be found using the formula SA = B + Ph, where B is the area of the base, P is the perimeter of the base, and h is the height of the vase. Since the vase has a circular base, the area of the base can be found using the formula for the area of a circle: B = πr², where r is the radius of the base.
The diameter of the vase is 4.3 inches, so the radius is half of that, or 2.15 inches. The area of the base is therefore:
B = πr² = 3.14 * (2.15)² ≈ 14.46 square inches.
The perimeter of the base is the circumference of the circle, which can be found using the formula C = 2πr:
P = 2πr = 2 * 3.14 * 2.15 ≈ 13.53 inches.
Now we can use the formula SA = B + Ph to find the surface area of the vase:
SA = B + Ph = 14.46 + 13.53 * 11 ≈ 168.39 square inches.
Rounding to the nearest tenth of a square inch, the surface area of the vase is approximately 168.4 square inches.
To know more about cylinders visit:
brainly.com/question/15891031
#SPJ1
Which relation represents a function?
StartSet (0, 0), (2, 3), (2, 5), (6, 6) EndSet
StartSet (3, 5), (8, 4), (10, 11), (10, 6) EndSet
StartSet (negative 2, 2), (0, 2), (7, 2), (11, 2) EndSet
StartSet (13, 2), (13, 3), (13, 4), (13, 5) EndSet
Answers
Answer:
(-2, 2), (0, 2), (7, 2), (11, 2)
Step-by-step explanation:
A relation must have no repeating x-values for it to be a function.
Set C does not have any repeating x-values, so it is a function.
Sets A, B, and D have repeating x-values, so they are not functions.
A: (0, 0), (2, 3), (2, 5), (6, 6)
B: (3, 5), (8, 4), (10, 11), (10, 6)
D: (13, 2), (13, 3), (13, 4), (13, 5)
Answer:
c
Step-by-step explanation:
hope this helps
Susan’s apartment is shown below. Assuming that all rooms are rectangular, find the areas described below. All measurements are in feet
Answers
the camera cost $540 if the sales tax is 7.2% what is the tax change and the total cost?
Answers
Answer:
38.88
Step-by-step explanation:
Convert the problem to an equation using the percentage formula: P% * X = Y.
P is 10%, X is 150, so the equation is 10% * 150 = Y.
Convert 10% to a decimal by removing the percent sign and dividing by 100: 10/100 = 0.10.
which of these is most likely to weigh 2 kilograms car roast chicken horse egg tea bag
Answers
The item most likely to weigh 2 kilograms is a roast chicken.
Which of them would weight 2 kilograms?
The size, breed, and any other ingredients or stuffing used can all affect the weight of a roast chicken. Weights of roast chickens can range from petite ones weighing less than 1 kilogram to larger ones weighing more than 2 kilograms.
The other things that we have there would either weigh less than 2 Kg such as a tea bag or much more than 2 Kg such as a horse. The egg and the tea a very light and would be less than 2 Kg in weight while the bag and the horse would be above 2 Kg in weight.
Learn more about weight:https://brainly.com/question/31659519
#SPJ1
please help me it’s urgent !!

Answers
Answer:
3>x
Step-by-step explanation:
Answer:
less than 3 (x < 3)
Step-by-step explanation:
Prove the following this?
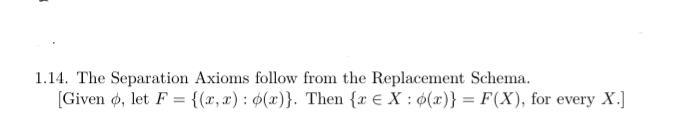
Answers
Answer:
The replacement axiom (axiom scheme) is the most general form you need, essentially saying that if you have a function whose domain is a set then the image is also a set. Furthermore, the empty set can be inferred by an existence of any set at all, when combined with separation (and hence, can be inferred by replacement).
Formally speaking the replacement schema says that for every formula φ(u,v,p1,…,pn)
, fix the parameters p1,…,pn
and pick any set A
, whenever u∈A
has at most one v
for which φ(u,v,p1,…,pn)
is true, then the collection of {v∣φ(u,v,p1,…,pn),u∈A}
is also a set.
How to infer separation and pairing? Simple.
First we infer separation. Given ϕ(x)
, we simply define φ(u,v,p)
to be
φ(u,v,p)=defu=v∧u∈p∧ϕ(u)
This is a functional formula (i.e. for every u
there is at most a single v
for which φ(u,v,p)
holds) and it is easy to verify that the image of φ(u,v,a)
is indeed {x∈a∣ϕ(x)}
.
The empty set exists by separation - simply take some a
(which exists because we assume there is some set in the universe) and the function ϕ(x):=x≠x
.
As you noted, {∅,P(∅)}
exists by the Power set axiom.
Now for a given x,y
we want to have {x,y}
so we define the following φ(u,v)
as following:
φ(u,v):=(u=∅∧v=x)∨(u=P(∅)∧v=y)
Note that φ
is a functional formula, i.e. for a given u
there is only one v
for which φ(u,v)
is true. By the axiom of replacement we have now that {x,y}
is a set. Therefore the axiom of pairing holds if we assume Power set and Replacement.
Now we have two ways of looking at ZFC. Sometimes we want to prove that something is a model for ZFC and need to verify the list of axioms in which case proving both Separation and Replacement is completely redundant. At other times we want to prove certain things which are quicker when using the more specific axioms (e.g. pairing (or even ordered pairing, which can be quickly inferred from pairing itself)).
This is a sort of freedom that we allow ourselves. We add extra axioms that we don't really need. Then if we want to ensure all the axioms hold we check for the "core" of the axiomatic system, and when we want to ease on ourselves in other cases we can just use the extra axioms for our convenience.
Step-by-step explanation:
Helppp pleasee!!
In your own words, write a definition for sales tax.
2) If you buy a meal from a restaurant that costs $15.00, and the tax is 7%, how much do you pay in taxes?
- Explain in detail, the steps you would take to solve this sales tax question.
Answers
The value of the tax for the meal is $1.05.
What Is a Sales Tax?The government levies a consumption tax known as a sales tax on the purchase of goods and services. At the point of sale, a standard sales tax is imposed, collected by the shop, and paid to the government.
Depending on the regulations in that country, a business may be responsible for sales taxes in that jurisdiction if it has a presence there, which can be a physical site, an employee, or an associate.
Given the cost of the meal = $15.00
and rate of tax = 7%
converting the rate of tax into decimal form,
rate of tax = 7% = 7/100
rate of tax = 0.07
amount of tax = cost x rate of tax
amount of tax = 15 x 0.07
amount of tax = $1.05
Hence the amount of tax is $1.05.
Learn more about sales tax;
https://brainly.com/question/29442509
#SPJ1
An equation of a circle is given as (x + 6)2 + (y − 7)2 = 81. Find the center and radius of the circle.
Answers
The equation of a circle is written as (x – h)^2 + (y – k)^2 = r^2
h and k are the center point and r is the radius.
In the given equation h = -6 and k = 7 and r would be the square root of 81, which is 9.
Center (-6,7)
Radius = 9
The required center is \((-6,7)\) and the radius is 9 units.
Given equation is,
\((x + 6)^2 + (y-7)^2 = 81\)....(1)
Equation of the circle: The general equation of the circle with the center (a,b) and the radius r is represented by,
\((x-a)^2+(y-b)^2=r^2\)...(2)
We can write the given equation as,
\((x + 6)^2 + (y-7)^2 = (9)^2\)
Comparing equations (1) and (2) we get,
The Centre of the given circle is \((-6,7)\)
The radius of the given circle is 9 units.
Learn more about the equation of the circle:
https://brainly.com/question/519358
sin(x)-cos(x)/sin²(x)-cos²(x) = 1

Answers
The prove of the given trigonometric function is given below.
The given trigonometric function is,
(sin⁴(x) - cos⁴(x))/(sin²(x) - cos²(x))
Now proceed left hand side of the given expression:
We can write the expression as,
⇒[(sin²(x))² - (cos²(x))²]/(sin²(x) - cos²(x))
Since we know that ,
Algebraic identity:
a² - b² = (a-b)(a+b)
Therefore the above expression be
⇒(sin²(x) - cos²(x))(sin²(x) + cos²(x))/(sin²(x) - cos²(x))
⇒(sin²(x) + cos²(x))
Since we know that,
Trigonometric Identities come in handy when trigonometric functions are used in an expression or equation. Trigonometric identities hold for all values of variables on both sides of an equation. Geometrically, these identities include one or more trigonometric functions (such as sine, cosine, and tangent).
Then,
sin²(x) + cos²(x)² = 1 is an trigonometric identity
Hence,
(sin⁴(x) - cos⁴(x))/(sin²(x) - cos²(x)) = 1
Hence proved.
Learn more about the triangle visit;
brainly.com/question/1058720
#SPJ1
Mary wants to buy a new iPhone for $699. she has $200 saved and plans to save $45 per week. How many weeks will it take Mary to have at least $699 to buy her phone?
Answers
I really really don't know
The degree of the sum of the expressions x⁴ +4y₂ -5xy and x₃ - y + 2xy
Answers
Answer:
4.
Step-by-step explanation:
Degree will he 4, since the largest exponent will still be 4 after the addition.
Answer:
Step-by-step explanation:
\(x^{4} +4y^{2} -5xy + x^{3} -y+2xy=x^{4}+x^{3}+4y^{2-y-3xy\)
Therefore, grade of the sum is 4.
graph the line with slope -3/4 passing through the point (2,-1)
Answers
Answer:
Step-by-step explanation:
Slope of the line:
\(m = \frac{y-y1}{x-x1} \\\)
Given:
slope = -3/4
point (x1,y1) = (2, -1)
Substitute and solve
\(m = \frac{y-y1}{x-x1} \\-\frac{3}{4} = \frac{y-(-1))}{x-2} \\-3(x-2) = 4(y+1)\\-3x + 6 = 4y + 4 \\Transpose\\4y = -3x + 6 - 4\\4y = -3x + 2 \\y = -3/4x + 2/4\\y = -3/4x + 1/2\\OR\\4y +3x - 2 = 0\)
1/2 is the y-intercept
(0,1/2)
Since we have 2 points already, we can then graph the line.
(2, -1) and (0, 1/2)

What is the equation of the following line? Be sure to scroll down first to see all answer options. (2,10) (0,0)
A. y= 1/5x
B. y = 5x
C. y = 6x
D. y = -6x
E. y = -5x
please help asap
Answers
Answer:
○ B. \(\displaystyle y = 5x\)
Step-by-step explanation:
\(\displaystyle \frac{-y_1 + y_2}{-x_1 + x_2} = m \\ \\ \frac{-10 \pm 0}{-5 \pm 0} = m \hookrightarrow \frac{-10}{-2} = m; 5 = m \\ \\ \boxed{y = 5x}\)
This is considered direct variation because the line intersects the origin.
I am joyous to assist you at any time.
A car purchased for $15,000 depreciates under a straight-line method in the
amount of $950 each year. Which equation below best models this
depreciation?
A. y = 15000x-950
OB. y = 15000 +950x
OC. y = 15000-950x
OD. y = 15000x+950
Answers
Answer:
i can't send full page of it sorry

The equation y = 15000 - 950x best models the depreciation.
Option C is the correct answer.
What is an equation?An equation contains one or more terms with variables connected by an equal sign.
Example:
2x + 4y = 9 is an equation.
2x = 8 is an equation.
We have,
The equation y = 15000 - 950x.
Here, y represents the value of the car after x years.
The initial value of the car is $15,000, which means the value of the car at x = 0 is $15,000.
The car depreciates by $950 each year, so after one year, the value of the car will be $15,000 - $950 = $14,050.
After two years, the value of the car will be $14,050 - $950 = $13,100, and so on.
This linear relationship between the value of the car and the number of years can be modeled by the equation y = 15000 - 950x,
where 15000 is the initial value and -950x represents the amount of depreciation each year.
Thus,
The equation y = 15000 - 950x best models the depreciation.
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ5
Consider the quadratic function f(x) = x2 – 5x + 12. Which statements are true about the function and its graph? Select three options. The value of f(–10) = 82 The graph of the function is a parabola. The graph of the function opens down. The graph contains the point (20, –8). The graph contains the point (0, 0).
Answers
The true statements are
The value of f(–10) = 82
The graph of the function is a parabola.
The graph contains the point (20, –8).
What is a Parabola:A parabola is a type of conic section that is formed when a plane intersects a cone in such a way that the angle between the plane and the vertical axis of the cone is equal to the angle between the plane and a generator (a straight line passing through the vertex and the base of the cone).
The resulting shape is a symmetrical, U-shaped curve. The standard form of the parabola is a quadratic function.
Here we have
The quadratic function f(x) = x²/5 – 5x + 12
Now check each option as follows
1. The value of f(–10) = 82
To check this find f(-10) as follows
f(-10) =1/5 (-10)²– 5(-10) + 12 = 20 + 50 + 12 = 82
Hence, The value of f(–10) is equal to 82
2. The graph of the function is a parabola.
As we know the standard equation of a parabola is a quadratic function that is in the form of ax² + bx + c
Hence, the quadratic function represents a parabola
3. The graph of the function opens down.
In the given function f(x) = x²– 5x + 12, the coefficient of the x² term is 1. Since the coefficient of x² is positive, the parabola opens upwards.
Hence, The graph of the function opens down is false
4. The graph contains the point (20, –8).
To check this substitute the point in f(x)
=> –8 = 1/5(20)²– 5(20) + 12
=> –8 = 80 – 100 + 12
=> –8 = –8 [ Which is true ]
Hence, The graph contains the point (20, –8).
5. The graph contains the point (0, 0).
=> 0 = (0)²– 5(0) + 12
=> 0 = 12 [ which is not true ]
Hence, The graph doesn't contain the point (0, 0).
Therefore,
The true statements are
The value of f(–10) = 82
The graph of the function is a parabola.
The graph contains the point (20, –8).
Learn more about Parabola at
https://brainly.com/question/21685473
#SPJ9
Someone please help me

Answers
Answer:
The third option
Step-by-step explanation:
If you plug -4 in for x in the first option, you would get 12 + which is 14 and
14 ≠ 5.
If you plug in -4 for the second option you would have -0.75 times -4 which is 3 and 3 plus 8/3 would not give you a whole number so it is not equal to 5.
If you plug in -4 to the third option you would get -4 times -0.75 which is 3 and 3 + 2 = 5. But to check the rest of the numbers you would plug in 0 for x and get -0.75 times 0 is 0 and 0 + 2 = 2.
For the last option, just to eliminate all other options, if you plug in -4 for x you would have 2 times -4 which is -8 and -8 - 0.75 would not be a whole number so it could not be 5.
51.5:1.2=
|
What is the answer to 1.5 divided by 1.2
Answers
Answer:
1.25
Step-by-step explanation:
1.5 divided by 1.2 is 1.25
Hope this helps☺️
Answer:
1.25
Step-by-step explanation:
1.5 / 1.2 = 15/12 = 5/4 = 1 1/4 = 1.25
Question 2
A box contains 22 coloured pencils.
6 pencils are pink, 9 pencils are blue and 7 pencils are yellow.
Write down the ratio pink pencils : not pink pencils.
Give your answer in its simplest form.
Answers
Answer:
3/8 or 3:8
Step-by-step explanation:
pink : not pink
6 : 16
Think of it as a fraction. Simplify it in the same way.
6/16 simplifies to 3/8
So the pink:notpink ratio is 3/8 or 3:8
when simplified it becomes 3:8
Pls answer this fast

Answers
Answer: C
Step-by-step explanation:
1. divide 3 by 2 to find out how many pounds of blueberries she picked each day. 3/2 is 1.5
2. multiply 1.5 by 16 to convert to ounces. 1.5x16 is 24.
3. she picked 24 ounces of blueberries each day.
7 and a number equals 21

Answers
Answer:
7x3=21
Step-by-step explanation:
7+7+7=21, 7x3=21
A jar of peanut butter contains 50 tablespoons of peanut butter.
How many sandwiches can you make from the jar of peanut butter, assuming you have plenty of bread and jelly?
A. 25 sandwiches
B. 9 sandwiches
C. 10 sandwiches
D. 50 sandwiches

Answers
Answer:
the correct answer is A. 25 sandwiches.
Step-by-step explanation:
Assuming you have plenty of bread and jelly, you can make 25 sandwiches from the jar of peanut butter.
Each sandwich typically requires 2 tablespoons of peanut butter, one slice of bread with peanut butter and one slice of bread with jelly.
So, if you have 50 tablespoons of peanut butter, you can make 25 sandwiches with it, because 50 / 2 = 25.
Therefore, the correct answer is A. 25 sandwiches.
Answer: 25
Step-by-step explanation:
We have 50 tablespoons of peanut butter and we know that it requires 2 tablespoons to make a single sandwich. In order to find how many sandwiches we can make with our 50 tablespoons, we would have to do 50 divided by 2.
2+2...=50
The sides of a triangle are 21 ,29 , and 11 . Use the Pythagorean Theorem to determine if the triangle is right, acute, or obtuse. The triangle is because the square of the largest side the sum of the squares of the other two sides.
Answers
The triangle is obtuse because 11^2 + 21^2 does not equal 29^2.
The Pythagorean Theorem states that the sum of the squares of the two shorter sides of a triangle must equal the square of the longest side in order for the triangle to be a right triangle.
We can use this theorem to determine the type of triangle by calculating the square of the longest side (29^2), and then comparing it to the sum of the squares of the other two sides (11^2 + 21^2). Since 11^2 + 21^2 does not equal 29^2, the triangle is obtuse.
The Pythagorean Theorem states that the sum of the squares of the two shorter sides of a triangle must equal the square of the longest side in order for the triangle to be a right triangle.
Learn more about triangle here
https://brainly.com/question/2773823
#SPJ4
ILL GIVE BRAINLIEST PLS HELP

Answers
Answer:
A
Step-by-step explanation:
a translation 16 units to the left will replace x with x+16, and a translation 6 units down will replace g(x) with g(x)-6, so it's A.