ASAP! GIVING BRAINLIEST! Please read the question THEN answer correctly! No guessing. Show your work or give an explaination.

Answer:

The Expression is : J2-74

Answer:

Step-by-step explanation:

To show that the expression \(\ln(\sqrt{2} + 1) - \ln\left(\frac{1}{\sqrt{2}}\right)\) is equal to \(-\ln\left(1 - \frac{1}{\sqrt{2}}\right)\), we can simplify both sides of the equation using the properties of logarithms. Here are the steps:

Step 1: Simplify the expression on the left side:

\(\ln(\sqrt{2} + 1) - \ln\left(\frac{1}{\sqrt{2}}\right)\)

Step 2: Apply the logarithmic property \(\ln(a) - \ln(b) = \ln\left(\frac{a}{b}\right)\) to combine the logarithms:

\(\ln\left(\frac{\sqrt{2} + 1}{\frac{1}{\sqrt{2}}}\right)\)

Step 3: Simplify the expression within the logarithm:

\(\ln\left(\frac{(\sqrt{2} + 1)}{\left(\frac{1}{\sqrt{2}}\right)}\right)\)

Step 4: Simplify the denominator by multiplying by the reciprocal:

\(\ln\left(\frac{(\sqrt{2} + 1)}{\left(\frac{1}{\sqrt{2}}\right)} \cdot \sqrt{2}\right)\)

\(\ln\left(\frac{(\sqrt{2} + 1) \cdot \sqrt{2}}{\left(\frac{1}{\sqrt{2}}\right) \cdot \sqrt{2}}\right)\)

\(\ln\left(\frac{(\sqrt{2} + 1) \cdot \sqrt{2}}{1}\right)\)

Step 5: Simplify the numerator:

\(\ln\left(\frac{(\sqrt{2} + 1) \cdot \sqrt{2}}{1}\right)\)

\(\ln\left(\sqrt{2}(\sqrt{2} + 1)\right)\)

\(\ln\left(2 + \sqrt{2}\right)\)

Now, let's simplify the right side of the equation:

Step 1: Simplify the expression on the right side:

\(-\ln\left(1 - \frac{1}{\sqrt{2}}\right)\)

Step 2: Simplify the expression within the logarithm:

\(-\ln\left(\frac{\sqrt{2} - 1}{\sqrt{2}}\right)\)

Step 3: Apply the logarithmic property \(\ln\left(\frac{a}{b}\right) = -\ln\left(\frac{b}{a}\right)\) to switch the numerator and denominator:

\(-\ln\left(\frac{\sqrt{2}}{\sqrt{2} - 1}\right)\)

Step 4: Simplify the expression:

\(-\ln\left(\frac{\sqrt{2}}{\sqrt{2} - 1}\right)\)

\(-\ln\left(\frac{\sqrt{2}(\sqrt{2} + 1)}{1}\right)\)

\(-\ln\left(2 + \sqrt{2}\right)\)

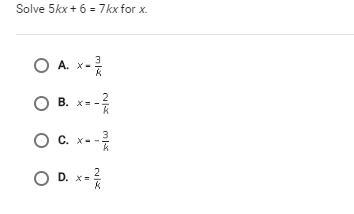
As we can see, the expression \(\ln(\sqrt{2} + 1) - \ln\left(\frac{1}{\sqrt{2}}\right)\) simplifies to \(\ln(2 + \sqrt{2})\), which is equal to \(-\ln\left(1 - \frac{1}{\sqrt{2}}\right)\).

Step-by-step explanation:

y = -1/2 X + 1/4

comparing with y = mx+c

m = -1/2 and m is slop

henve slope = -1/2

Solving the provided question, we can say that the quadratic equation is \((x - 1)(x^{2} + 3x - 4)\) = \(x^{3} + 2x^{2} - 7x + 4\) and the roots of the polynomial are x = 1, -1, 4.

A quadratic polynomial in a single variable is represented by the equation  \(ax^{2}+bx+c=0\). a 0. Since this polynomial is of second order, the Fundamental Theorem of Algebra guarantees that it has at least one solution. There are both simple and complex solutions.

A quadratic equation is just that—quadratic. It has at least one word that has to be squared, as shown by this. One of the often used solutions for quadratic equations is "ax2 + bx + c = 0." where X is an undefined variable and a, b, and c are numerical coefficients or constants.

the quadratic equation is

\((x - 1)(x^{2} + 3x - 4)\) = \(x^{3} + 2x^{2} - 7x + 4\)

On multiplying,

⇒ \(x (x^{2} + 3x - 4) - (x^{2} + 3x - 4)\)

⇒ \(x^{3} + 3x^{2} - 4x - x^{2} - 3x + 4\)

⇒ \(x^{3} + 2x^{2} - 7x + 4\)

∴ We can say that LHS = RHS.

From given equation, the roots of the equation will be  -

\((x - 1)(x^{2} + 3x - 4)\)

⇒ x - 1 = 0

⇒ x = 1

\(x^{2} + 3x - 4 = 0\)

⇒ \(x^{2} - 4x + x - 4\)

⇒ \(x(x - 4) + 1(x - 4)\)

⇒ (x + 1) (x - 4)

⇒ x = -1, x = 4

To know more about quadratic equation visit:

brainly.com/question/30098550

#SPJ1

Answer:

x = 1

Step-by-step explanation:

First, you have to eliminate the "2," leaving it as, 6x=6.

Then divide, which will leave the equation to x=1.

Answer:

x=11, y=1 or (11, 1)

Step-by-step explanation:

I used substitution to solve this. Basically wherever there's an x, I would fill it in as 12-y.

2(12-y)+3y=29

24+2y+3y=29

24+5y=29

subtract 24 from both sides

5y=5

divide by 5

y=1

Now substitute y back in to get x.

x=12-1

x=11

You can also graph this into desmos, and wherever they intercept, that's your answer.  I hope this helps!

Answer:

(P,O)(M,N)(M,P)(N,O)

Step-by-step explanation:

brainliest pleeez

Answer:

C

<$&#&#;#;#;#;#

Step-by-step explanation:

1/4= 4x6=24

Answer:

C

Step-by-step explanation:

Answer:

I'm gonna say b

Step-by-step explanation:

b should be the answer

Answer:

35/3 yd

Step-by-step explanation:

first convert the hypotenuse into 37/3, then you can write (37/3)^2-(4)^2=a^2. solve to get 35/3

Answer:

B

D

D

Step-by-step explanation:

please verify and rate 5 stars and say thank you

Using the Central Limit Theorem, it is found that the distribution of the sample means of the weights of the 7 adult standard poodles is normal, with mean of 50 pounds and standard deviation of 5.67 pounds.

The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).

In this problem, for the population, \(\mu = 50, \sigma = 15\).

The distribution of the sample means of the weights of the 7 adult standard poodles is normal, with mean of 50 pounds and standard deviation of 5.67 pounds.

A similar problem is given at https://brainly.com/question/25606713

The solution to the equation is given by:

F. x = √10 + 2/5

What is the equation?

It is given by:

(5x-2)²=10

First, we apply the square root to both sides to remove the square, hence:

√(5x-2)²=√10

5x-2=√10

Then, isolating x:

5x = √10+2

x = √10+2/5

Given by option F, which is the solution.

Learn more about equations here:

brainly.com/question/25537936

#SPJ9

Answer:

The correct answer is:

Option A: A 10x — 15000 ≥ 50000

Step-by-step explanation:

Given that the total cost of manufacturing by the company is $15000.

Let x be the number of gallons the company sells.

It is also mentioned that the company earns $10 on each gallon.

So the total profit will be the the difference of the selling cost of gallons and manufacturing cost

Mathematically,

\(10x-15000\)

Now it is mentioned that the profit should be at least 50000 dollars which means the profit can be minimally 50000 and also can be greater than it so

\(10x-15000 \geq 50000\)

The number of gallons can be found by solving the obtained inequality.

Hence,

The correct answer is:

Option A: A 10x — 15000 ≥ 50000

To begin we need to find the value of a

We apply the Pythagorean theorem

Now we find theta

Here we use the tangent that is the oppositive side over the adjacent side

There are countless possibilities for shapes that are similar but not congruent to shape 1, as long as they maintain the same proportions and shape.

There are many shapes that are similar but not congruent to shape 1. Similar shapes have the same shape, but their sizes may be different. In contrast, congruent shapes have the same shape and size.

One example of a similar shape to shape 1 is a rectangle that is twice as long and half as wide. Another example could be a square that is three times larger in area than shape 1.

A parallelogram that has the same base as shape 1 but is three times as tall is also similar but not congruent.

To learn more about : congruent

https://brainly.com/question/29789999

#SPJ8

Answer:

Step-by-step explanation:

If Jamal has 8 times the number of eggs then Krystal has \(1\frac{1}{3}\)   fraction of eggs.

A fraction represents a part of a whole.

Given that Krystal placed one egg in a carton that holds six eggs

Krystal has 1 egg out of a carton that holds 6 eggs, so she has 1/6 of a carton.

Jamal has 8 times the number of eggs Krystal has, so he has:

8 x (1/6)

Eight times of one by six

= 8/6

Divide numerator and denominator by two

= 4/3

The given fraction 4/3 is converted to mixed fraction

=\(1\frac{1}{3}\)

The fraction that shows how many eggs Jamal has is \(1\frac{1}{3}\).

Hence, if Jamal has 8 times the number of eggs then Krystal has \(1\frac{1}{3}\)   fraction of eggs.

To learn more on Fractions click:

https://brainly.com/question/10354322

#SPJ2

Answer:

4/99

Step-by-step explanation:

Answer:

The sine function is:

\(y(x)=\frac{2}{3}sin[3\pi (x-\frac{2\pi}{3})]-2\)

Step-by-step explanation:

We need to recall that a sine function can write as:

\(y(x)=Asin[B(x+C)]+D\)

Where:

So we just need to use the listed attributes

Therefore, the sine function is:

\(y(x)=\frac{2}{3}sin[3\pi (x-\frac{2\pi}{3})]-2\)

I hope it helps you!

This question uses the experimental study concept.

Doing this, we have that the walls analyzed are the individuals.

First, the concept of experimental study is presented:

In this question:

There is an intervention in the walls, they are painted, using three different paint compositions, and then they are exposed to sunlight, and after that the walls were analyzed, to study the degree of change in pigment of the paint, being compared between different paint compositions.

Thus, since the intervention was in the walls, they are the individuals in this experiment.

A similar question is found at https://brainly.com/question/24321224

Answer:

x is -7.5 or -14/2 or -7½

Step-by-step explanation:

- Supposing y varies directly with x

\( { \tt{y \: \alpha \: x}} \\ \: \: \: \: { \tt{y = kx}} \)

[k is a constant of proportionality (k ≠ 0)]

- When y is 6, x is -2

\( \: \: \: \: \: \: \: \: \: { \tt{6 = (k \times ^{ - }2) }} \\ { \tt{6 = - 2k}} \\ { \tt{k = - 3 \: \: }}\)

- Therefore, the equation is;

\({ \boxed{ \tt{y = - 2x}}}\)

- What is x when y is 15

\({ \tt{15 = - 2x}} \\ { \tt{x = - 7.5}}\)

The value of x is -5

The equation for a direct variation is y = kx, where k is the constant of variation. Since we know that y = 6 when x = -2, we can solve for k:

                                        k = y/x

                                        k = 6/-2

                                        k = -3

Therefore, the equation for this direct variation is y = -3x. To find x when y = 15, Substitute k = -3 and y = 15 into the equation

                                15 = -3x

Then solve x,

                       x = \(\frac{-15}{3}\)

                        x = -5

Therefore, when y = 15, x = -5.

Learn how to solve equation:

brainly.com/question/26260688

Answer: D

Step-by-step explanation:

2x-36=0                                                

+36     +36

___________

2x=36

x=18

Even if one equation, -18 was not solved, you can easily cross out the ones without 18 and get the answer.

Answer:

39

Step-by-step explanation:

12+20+22+22+23=99

new mean=23

23*6=138

138-99=39

Answer:

513,730

Step-by-step explanation:

You times 17,900 by 28.7 to get 513,730.

Answer:

Step-by-step explanation:

To find the area of the shaded region, we need to first find the x-coordinates of the points where the two functions intersect. We can set f(x) = g(x) and solve for x:

x^4 - 12x^3 + 48x^2 = 44x + 105

x^4 - 12x^3 + 48x^2 - 44x - 105 = 0

We can use a numerical method, such as the Newton-Raphson method, to approximate the roots of this equation. Using a graphing calculator or computer algebra system, we can find that the roots are approximately:

x = -1.932, x = 0.695, x = 4.149

Note that the root x = -1.932 is outside the given interval [3, 4], so we can ignore it.

The shaded region is bounded by the x-axis, the line y = 340, and the graphs of f(x) and g(x) between x = 3 and x = 4. To find the area of this region, we can integrate the difference between the two functions over this interval:

A = ∫3^4 [g(x) - f(x)] dx

A = ∫3^4 [44x + 105 - (x^4 - 12x^3 + 48x^2)] dx

A = ∫3^4 [-x^4 + 12x^3 - 48x^2 + 44x + 105] dx

We can integrate term by term using the power rule:

A = [-x^5/5 + 3x^4 - 16x^3 + 22x^2 + 105x]3^4

A = [-1024/5 + 192 - 192 + 22 + 105] - [-81/5 + 108 - 192 + 66 + 105]

A = 347.2

Therefore, the area of the shaded region is approximately 347.2 square units.

In the order provided in the question, X is a discrete random variable, Y is not a random variable, U is a discrete random variable, X is a continuous random variable, Z is a continuous random variable, Y is a continuous random variable, X is a continuous random variable, and X is a discrete random variable.

• X = the number of unbroken eggs in a randomly chosen standard egg carton The possible values for X are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, or 12, as an egg carton can have anywhere between 0 and 12 unbroken eggs. X is a discrete random variable since it takes on a finite number of possible values.

• Y = 5 the number of students on a class list for a particular course who are absent on the first day of classes The only possible value for Y is 5, so it is not a random variable.

• U = 5 the number of times a duffer has to swing at a golf ball before hitting it The possible values for U are all positive integers starting from 5. U is a discrete random variable since it takes on a countable number of possible values.

• X = 5 the length of a randomly selected rattlesnake. The possible values for X are all positive real numbers. X is a continuous random variable since it can take on any value within a range of values.

• Z = 5 the sales tax percentage for a randomly selected amazon.com purchase The possible values for Z are all percentages between 0% and 100%, including decimal values. Z is a continuous random variable since it can take on any value within a range of values.

• Y = 5 the pH of a randomly chosen soil sample. The possible values for Y are all positive real numbers. Y is a continuous random variable since it can take on any value within a range of values.

• X = 5 the tension (psi) at which a randomly selected tennis racket has been strung. The possible values for X are all positive real numbers. X is a continuous random variable since it can take on any value within a range of values.

• X = 5 the total number of times three tennis players must spin their rackets to obtain something other than UUU or DDD (to determine which two play next) The possible values for X are 1, 2, 3, and so on, since the players can keep spinning the rackets indefinitely. X is a discrete random variable since it takes on a countable number of possible values.

Learn more about continuous random variable here brainly.com/question/17238189

#SPJ4

They can buy 120 vans, 60 small trucks, and 80 large trucks.

The truck company plans to spend 10 million on 260 vehicles. Each commercial van cost 25,000 dollars. Each small truck 50,000 dollars and each large truck 50,000 dollars. They needed twice as many van as small truck

Therefore,

let

s = number of small truck

number of van = v

let

l = number of large truck

v + s + l = 260

25,000(v) + 50,000(s) + 50,000(l) = 10,000, 000

v + 2s + 2l = 400

Hence,

v = 2s

So,

2s + 2s + 2l = 400

4s + 2l = 400

2s + s + l = 260

3s + l = 260

2s + l = 200

s = 60

l = 200 - 2(60)

l = 200 - 120

l = 80

v = 2(600 = 120

Therefore, they can buy the following:

number of small truck = 60

number of van = 120

number of large truck = 80

learn more on cost here: brainly.com/question/27903912

#SPJ1