Answers
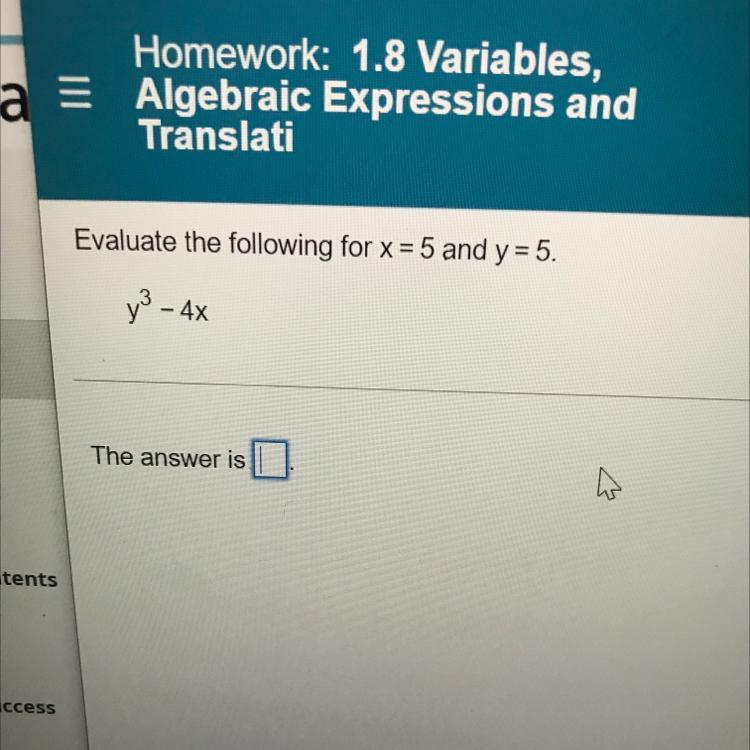
5^2-4(5)
25-20
5
Answer:
105
Step-by-step explanation:
5^3-4(5)
5^3=125
4x5=20
125-20=105
Related Questions
1)
Find the value of x in
the triangle below:
17
A) 20.2
B) 18.7
C) 19.5
D) 21.1
E) 22.6
K
84⁰
65°
Mrs. Wilson
Mrs. Crane
Mr. Haynes
Ms. Lindstrom
Mr. Swasey
O Gina Wilson (All Things Algebra), 2014

Answers
The correct option is A) 20.2.
What is triangle sum?
The triangle sum is a property of triangles that states that the sum of the interior angles of a triangle is always equal to 180 degrees. In other words, if you add up the measures of the three angles inside a triangle, the result will always be 180 degrees.
Using the given information and the fact that the angles in a triangle sum to 180 degrees, we can find the value of x as follows:
Start by finding the measure of angle K by subtracting the measures of angles A and B from 180 degrees:
K = 180 - A - B
= 180 - 84 - 65
= 31 degrees
Use the law of sines to set up an equation relating the side lengths and corresponding angle measures:
sin(A)/x = sin(K)/17
Substitute the values we know into the equation and solve for x:
sin(84)/x = sin(31)/17
x = sin(84)*17/sin(31)
Using a calculator, we get:
x ≈ 20.2
Therefore, the value of x in the triangle is approximately 20.2.
So, the correct option is A) 20.2.
To know more about triangle sum visit:
https://brainly.in/question/28314721
#SPJ9
find the quotient, then check your answer using multiplication
Answers
X
Y
Which segment is the triangle?
Answers
Answer:
be more pacific
Step-by-step explanation:
HELP ME PLEASE!!
Twenty-four 10th graders were surveyed to find out what pets they had at home. Using the
data from the pie graph, determine the total number of students that have either a dog or a cat at home.
Show all your work. Explain in words how you found your answer. Tell why you took the steps you did to solve the problem!!

Answers
Answer:
15 tenth graders
Step-by-step explanation:
we can see that dogs take up 1/2 of the graph
birds take up 1/2 of 1/2 so they take up 1/4
other and cats together take up 1/4 of the graph which is 1/8 for each
you must add dogs and cats together and then multiply it bu 24
1/2 + 1/8
4/8 + 1/8 = 5/8
now multiply that by 24
24 * 5/8
\(\frac{24}{1} * \frac{5}{8} = \frac{3}{1} * \frac{5}{1} =15\)
that is the answer
ind the volume of the solid generated by revolving the region bounded by y=4sqrt(x) and the lines y = 12 and x = 0 about
A) the x axis B) the y axis C) the line y=12 D) the line x=9
Answers
To find the volume of the solid generated by revolving the region bounded by y=4√x and the lines y=12 and x=0 about the x-axis, y-axis, y=12 and x=9 respectively, we can use the disk or shell method.
For the x-axis, we can use the disk method. We first need to find the limits of integration. For the x-axis, our lower limit is 0 and our upper limit is 12. The radius of the disk is 4√x and the height of the disk is dx. Thus, the volume can be calculated as:
Vx = ∫0,12π(4√x)^2dx.For the y-axis, we can use the shell method. We first need to find the limits of integration. For the y-axis, our lower limit is 0 and our upper limit is 12. The radius of the shell is x and the height of the shell is 4√x. Thus, the volume can be calculated as:
Vy = ∫0,122πx(4√x)dx.For the line y=12, we can use the disk method. We first need to find the limits of integration. For the line y=12, our lower limit is 0 and our upper limit is 9. The radius of the disk is x and the height of the disk is dy. Thus, the volume can be calculated as:
V12 = ∫0,9πx^2dy.For the line x=9, we can use the shell method. We first need to find the limits of integration. For the line x=9, our lower limit is 0 and our upper limit is 12. The radius of the shell is 9 and the height of the shell is 4√x. Thus, the volume can be calculated as:
V9 = ∫0,124π9(4√x)dx.Once all the integrals have been calculated, the volume can be obtained by adding the results from all four integrals.
Learn more about integrals
https://brainly.com/question/28157330
#SPJ4
pls anyone help me with this question God PLSSS

Answers
Answer:
(6,4)
Step-by-step explanation:
Hope it helps you.......
Suppose that the derivable functions x=x(t) and y=y(t) satisfy xcosy=2.
If dx/dt=−2, find dy/dt when y=π/4.
a-) -√2 / 2
b-) 4
c-) -2√2
d-) √2
e-) 2√2
Please, someone help me!
Answers
Applying implicit differentiation, it is found that dy/dt when y=π/4 is of:
a-) -√2 / 2.
What is implicit differentiation?Implicit differentiation is when we find the derivative of a function relative to a variable that is not in the definition of the function.
In this problem, the function is:
xcos(y) = 2.
The derivative is relative to t, applying the product rule, as follows:
\(\cos{y}\frac{dx}{dt} - x\sin{y}\frac{dy}{dt} = 0\)
\(\frac{dy}{dt} = \frac{\cos{y}\frac{dx}{dt}}{x\sin{y}}\)
Since dx/dt=−2, we have that:
\(\frac{dy}{dt} = -2\frac{\cos{y}}{x\sin{y}}\)
When y = π/4, x is given by:
xcos(y) = 2.
\(x = \frac{2}{\cos{\frac{\pi}{4}}} = \frac{2}{\frac{\sqrt{2}}{2}} = \frac{4}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = 2\sqrt{2}\)
Hence:
\(\frac{dy}{dt} = -2\frac{\cos{y}}{x\sin{y}}\)
\(\frac{dy}{dt} = -\frac{1}{\sqrt{2}}\cot{y}\)
Since cot(pi/4) = 1, we have that:
\(\frac{dy}{dt} = -\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = -\frac{\sqrt{2}}{2}\)
Which means that option a is correct.
More can be learned about implicit differentiation at https://brainly.com/question/25608353
#SPJ1
Write the equation of the trigonometric graph.

Answers
Answer(s):
\(\displaystyle y = 3sin\: (1\frac{1}{2}x + \frac{\pi}{2}) - 2 \\ y = 3cos\: 1\frac{1}{2}x - 2\)
Explanation:
\(\displaystyle y = Asin(Bx - C) + D \\ \\ Vertical\:Shift \hookrightarrow D \\ Horisontal\:[Phase]\:Shift \hookrightarrow \frac{C}{B} \\ Wavelength\:[Period] \hookrightarrow \frac{2}{B}\pi \\ Amplitude \hookrightarrow |A| \\ \\ Vertical\:Shift \hookrightarrow -2 \\ Horisontal\:[Phase]\:Shift \hookrightarrow \frac{C}{B} \hookrightarrow \boxed{-\frac{\pi}{3}} \hookrightarrow \frac{-\frac{\pi}{2}}{1\frac{1}{2}} \\ Wavelength\:[Period] \hookrightarrow \frac{2}{B}\pi \hookrightarrow \boxed{1\frac{1}{3}\pi} \hookrightarrow \frac{2}{1\frac{1}{2}}\pi \\ Amplitude \hookrightarrow 3\)
OR
\(\displaystyle y = Acos(Bx - C) + D \\ \\ Vertical\:Shift \hookrightarrow D \\ Horisontal\:[Phase]\:Shift \hookrightarrow \frac{C}{B} \\ Wavelength\:[Period] \hookrightarrow \frac{2}{B}\pi \\ Amplitude \hookrightarrow |A| \\ \\ Vertical\:Shift \hookrightarrow -2 \\ Horisontal\:[Phase]\:Shift \hookrightarrow 0 \\ Wavelength\:[Period] \hookrightarrow \frac{2}{B}\pi \hookrightarrow \boxed{1\frac{1}{3}\pi} \hookrightarrow \frac{2}{1\frac{1}{2}}\pi \\ Amplitude \hookrightarrow 3\)
You will need the above information to help you interpret the graph. First off, keep in mind that although this looks EXACTLY like the cosine graph, if you plan on writing your equation as a function of sine, then there WILL be a horisontal shift, meaning that a C-term will be involved. As you can see, the photograph on the right displays the trigonometric graph of \(\displaystyle y = 3sin\: 1\frac{1}{2}x - 2,\) in which you need to replase "cosine" with "sine", then figure out the appropriate C-term that will make the graph horisontally shift and map onto the cosine graph [photograph on the left], accourding to the horisontal shift formula above. Also keep in mind that the −C gives you the OPPOCITE TERMS OF WHAT THEY REALLY ARE, so you must be careful with your calculations. So, between the two photographs, we can tell that the sine graph [photograph on the right] is shifted \(\displaystyle \frac{pi}{3}\:unit\) to the right, which means that in order to match the cosine graph [photograph on the left], we need to shift the graph BACK \(\displaystyle \frac{\pi}{3}\:unit,\) which means the C-term will be negative, and perfourming your calculations, you will arrive at \(\displaystyle \boxed{-\frac{\pi}{3}} = \frac{-\frac{\pi}{2}}{1\frac{1}{2}}.\) So, the sine graph of the cosine graph, accourding to the horisontal shift, is \(\displaystyle y = 3sin\: (1\frac{1}{2}x + \frac{\pi}{2}) - 2.\) Now, with all that being said, in this case, sinse you ONLY have a graph to wourk with, you MUST figure the period out by using wavelengths. So, looking at where the graph hits \(\displaystyle [0, 1],\) from there to \(\displaystyle [1\frac{1}{3}\pi, 1],\) they are obviously \(\displaystyle 1\frac{1}{3}\pi\:unit\) apart, telling you that the period of the graph is \(\displaystyle 1\frac{1}{3}\pi.\) Now, the amplitude is obvious to figure out because it is the A-term, but of cource, if you want to be certain it is the amplitude, look at the graph to see how low and high each crest extends beyond the midline. The midline is the centre of your graph, also known as the vertical shift, which in this case the centre is at \(\displaystyle y = -2,\) in which each crest is extended three units beyond the midline, hence, your amplitude. So, no matter how far the graph shifts horisontally, the midline will ALWAYS follow.
I am delighted to assist you at any time.


Zack opened a savings account and deposited 100.00 the account earns 10% interest compounded quarterly if he wants to use the money to buy a new bicycle in 2 years how much will he able to spend on the bike
Answers
Given information:
Deposit amount = P = $100
Interest rate = r = 10% = 0.10
Compounding interval = n = quarterly = 4
Number of years = t = 2
Solution:
Recall that the compound interest formula is given by
\(A=P(1+\frac{r}{n})^{n\cdot t}\)Where
A = Accumulated amount (or ending balance)
P = Principle amount (or deposit amount)
r = Interest rate in decimal
n = Number of compounding in a year
t = Number of years
Now let us substitute the given values into the above formula
\(\begin{gathered} A=100\cdot(1+\frac{0.10}{4})^{4\cdot2} \\ A=100\cdot(1+0.025)^8 \\ A=100\cdot(1.025)^8 \\ A=100\cdot(1.2184) \\ A=\$121.84 \end{gathered}\)Therefore, Zack will be able to spend $121.84 on the bike.
Determine whether each of the binary relation R defined on the given sets A is reflexive, symmetric, antisymmetric, or transitive. If a relation has a certain property, prove this is so; otherwise provide a counterexample to show that it does not. (a) A = Z: (a, b) E R if and only if ab > 0. (b) A = R: (a, b) R if and only if a^2=b^2 (c) A = N: (a, be R if and only if a/b is an integer.
Answers
Answer:
In explanation
Please let me know if something doesn't make sense.
Step-by-step explanation:
a)
*This relation is not reflexive.
0 is an integer and (0,0) is not in the relation because 0(0)>0 is not true.
*This relation is symmetric because if a(b)>0 then b(a)>0 since multiplication is commutative.
*This relation is transitive.
Assume a(b)>0 and b(c)>0.
Note: This means not a,b, or c can be zero.
Therefore we have abbc>0.
Since b^2 is positive then ac is positive.
Since a(c)>0, then (a,c) is in R provided (a,b) and (b,c) is in R.
*The relation is not antisymmretric.
(3,2) and (2,3) are in R but 3 doesn't equal 2.
b)
*This relation is reflective.
Since a^2=a^2 for any a, then (a,a) is in R.
*The relation is symmetric.
If a^2=b^2, then b^2=a^2.
*The relation is transitive.
If a^2=b^2 and b^2=c^2, then a^2=c^2.
*The relation is not antisymmretric.
(1,-1) and (-1,1) is in the relation but-1 doesn't equal 1.
c)
*The relation is reflexive.
a/a=1 for any a in the naturals.
*The relation is not symmetric.
Wile 4/2 is an integer, 2/4 is not.
*The relation is transitive.
If a/b=z and b/c=y where z and y are integers, then a=bz and b=cy.
This means a=cyz. This implies a/c=yz.
Since the product of integers is an integer, then (a,c) is in the relation provided (a,b) and (b,c) are in the relation.
*The relation is antisymmretric.
Assume (a,b) is an R. (Note: a,b are natural numbers.) This means a/b is an integer. This also means a is either greater than or equal to b. If b is less than a, then (b,a) is not in R. If a=b, then (b,a) is in R. (Note: b/a=1 since b=a)
Lease help me please thanks you

Answers
Answer:
x=6
Step-by-step explanation:
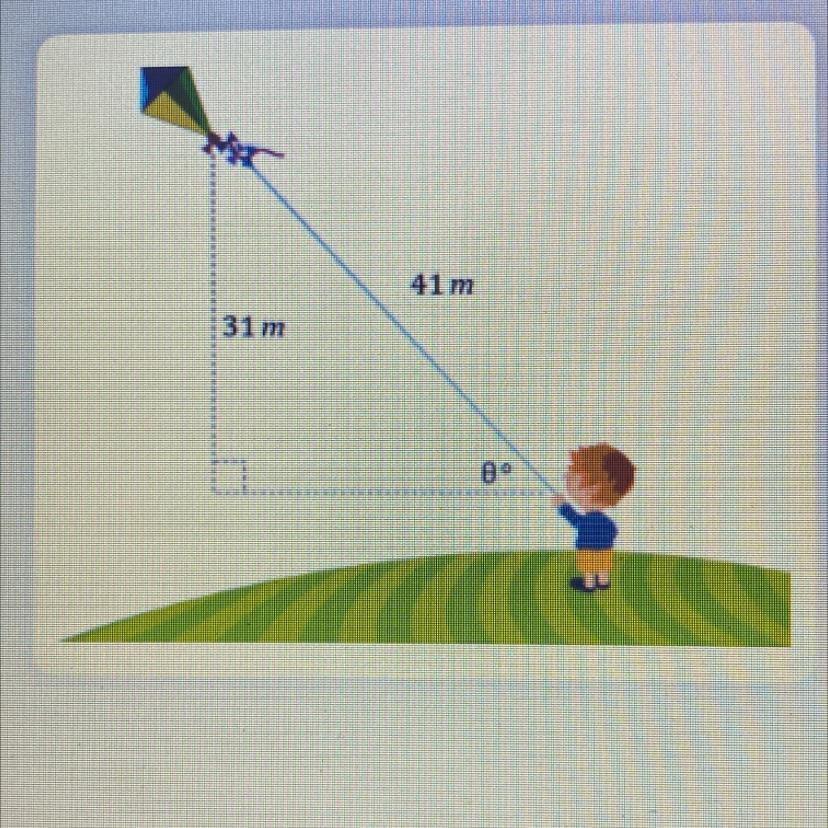
A boy flying his kite releases the entire length of his string which measures 41 m, so that the kite is 31 metres above him.If the angle the string makes with the horizontal ground is 0°, find 0 to two decimal places.
Answers
By definition,
sin(angle) = opposite/hypotenuse
From the picture,
\(\begin{gathered} \sin (\theta)=\frac{31}{41} \\ \theta=\arcsin (\frac{31}{41}) \\ \theta=49.12\text{ \degree} \end{gathered}\)There is a line that includes the point (1,6) and has a slope of 4. What is its equation in
slope-intercept form?
Write your answer using integers, proper fractions, and improper fractions in simplest form.
Answers
Answer:
y=4x+2
Step-by-step explanation:
So we start with the slope, which is bad.
But I have an idea
lets write it as
y=4x+? and since x=1 and y=6
6=4+?
Therefore, the y, intercept must be two
Answer:
y=4x+2
Step-by-step explanation:
y-y1=m(x-x1)
y-6=4(x-1)
y=4x-4+6
y=4x+2
The governor of state A earns $54,900 more than the governor of state B. If the total of their salaries is $310,850, find the salaries of each.
need to find a and b
Answers
Answer:
$127975, $182875
Step-by-step explanation:
Let the salary in state A be x. Then, the salary in state B is x+54900.
\(x+x+54900=310850 \\ \\ 2x=255950 \\ \\ x=127975 \\ \\ x+54900=182875\)
Solve these 4 equations. Tell me if they have one, none, or many solutions.
1. 3(x+4)=3x+11
2. -2(x+3)=-2x-6
3. 4(x-1) = 1/2(x-8)
4. 3x-7=4+6 +4x
Answers
Answer:
1. no solutions
2. many (infinite) solutions
3. one solution: x = 0
4. one solution: x = -17
Step-by-step explanation:
Question 1
\(\begin{aligned}&\textsf{Given equation}: & 3(x+4)&=3x+11\\&\textsf{Distribute}: & 3x+12&=3x+11\\&\textsf{Subtract }3x \textsf{ from both sides}: & 12 &=11\end{aligned}\)
As 12 ≠ 11 there are no solutions.
Question 2
\(\begin{aligned}&\textsf{Given equation}: & -2(x+3)&=-2x-6\\&\textsf{Distribute}: & -2x-6 &=-2x-6\\&\textsf{Add }2x \textsf{ to both sides}: & -6 &=-6\\&\textsf{Add }6 \textsf{ to both sides}: & 0 & = 0\\\end{aligned}\)
As 0 = 0 there are infinite (many) solutions.
Question 3
\(\begin{aligned}&\textsf{Given equation}: & 4(x-1) & =\dfrac{1}{2}(x-8)\\&\textsf{Distribute}: & 4x-4 &=\dfrac{1}{2}x-4\\&\textsf{Add }4 \textsf{ to both sides}: & 4x & = \dfrac{1}{2}x\\&\textsf{Subtract } \dfrac{1}{2}x \textsf{ from both sides}: & \dfrac{3}{2}x & = 0\\&\textsf{Divide both sides by } \dfrac{3}{2}: & x & = 0\end{aligned}\)
Therefore, there is one solution, x = 0.
Question 4
\(\begin{aligned}&\textsf{Given equation}: & 3x-7 & = 4+6+4x\\&\textsf{Simplify}: & 3x-7 & = 10+4x\\&\textsf{Swap sides}: & 10+4x & = 3x-7\\&\textsf{Subtract 10 from both sides}: & 4x & = 3x-17\\&\textsf{Subtract }3x \textsf{ from both sides}: & x & = -17\end{aligned}\)
Therefore, there is one solution, x = -17.
1. 3(x+4)=3x+11: No solutions.
2. -2(x+3)=-2x-6: Infinite solutions, any number can make the statement true.
3. 4(x-1) = 1/2(x-8): x= 0.
4. 3x-7=4+6 +4x: x= -17.
Step-by-step explanation:Equation 1.1. Write the expression.\(3(x+4)=3x+11\)
2. Simplify the left side of the equation by applying the associative property of multiplication.This is the rule we're applying: \(a(b+c)=(a*b)+(a*c)\).
\((3)(x)+(3)(4)=3x+11\\ \\3x+12=3x+11\)
3. Substract 3x from both sides.\(3x+12-3x=3x+11-3x\\ \\12=11\)
4. Conclude.As you may notice, we just obtained a false statement in subtitle 3, because 12 doesn't equal 11. Hence, this equation doesn't have solutions.
-------------------------------------------------------------------------------------------------------
Equation 2.1. Write the expression.\(-2(x+3)=-2x-6\)
2. Simplify the left side of the equation by applying the associative property of multiplication.\((-2)(x)+(-2)(3)=-2x-6\\ \\-2x-6=-2x-6\)
3. Conclude.Whenever we get an equation that has the same arguments on both sides, this means that there are infinite solutions to this equation, any value of x will make the equation true. Hence, the equation has infinite solutions.
-------------------------------------------------------------------------------------------------------
Equation 3.1. Write the expression.\(4(x-1) = 1/2(x-8)\)
2. Simplify the both sides of the equation by applying the associative property of multiplication.\((4)(x)+(4)(-1) = (\frac{1}{2} )(x)+(\frac{1}{2} )(-8)\\ \\4x-4=\frac{1}{2} x-4\)
3. Add 4 to both sides.\(4x-4+4=\frac{1}{2} x-4+4\\ \\4x=\frac{1}{2} x\)
4. Substract \(\frac{1}{2} x\) from both sides.\(4x-\frac{1}{2} x=\frac{1}{2} x-\frac{1}{2} x\\ \\4x-\frac{1}{2} x=0\\ \\4x-0.5x=0\\ \\3.5x=0\\ \\x=\frac{0}{3.5 } \\ \\x=0\)
5. Concluide.The solution for this equation is x= 0.
-------------------------------------------------------------------------------------------------------
Equation 4.1. Write the expression.\(3x-7=4+6 +4x\)
2. Simplify by completing the addition.\(3x-7=10 +4x\)
3. Add 7 to both sides.\(3x-7+7=10 +4x+7\\ \\3x=17+4x\)
4. Substract 4x from both sides.\(3x-4x=17+4x-4x\\ \\-x=17\)
5. Multiply bith sides by -1.\((-1)(-x)=(17)(-1)\\ \\x=-17\)
6. Conclude.The solution of this equation is x= -17.
On a graph, points are grouped to form a line with positive slope. Points (3, 9), (7, 1) and (11, 2) are not on the line.
Which points would be considered outliers?
Check all that apply.
(3, 9)
(4, 4)
(6, 5)
(7, 1)
(8, 7)
(11, 2)
none
Answers
Answer:
may i have brainiest please
Step-by-step explanation:

Answer:
the person above me or below me is correct
Step-by-step explanation:
Help me with this problem!!!!

Answers
For your first question (6), subtract the difference between the two points that I have circled. Each of those marks the upper quartile for each team.
For (7), I need to know which line or dot is 210. If it’s the line in the middle of the box, the answer is 50%. If it’s the line at the right side of the box, the answer is 75%
For (8), again, I need your help to know where 220 is.
If you can put some answers in the comments, I’m happy to keep helping you.

What are the exact solutions of x2 − 3x − 1 = 0 using x equals negative b plus or minus the square root of the quantity b squared minus 4 times a times c all over 2 times a? (1 point) x = the quantity of 3 plus or minus the square root of 5 all over 2 x = the quantity of negative 3 plus or minus the square root of 5 all over 2 x = the quantity of 3 plus or minus the square root of 13 all over 2 x = the quantity of negative 3 plus or minus the square root of 13 all over 2
Answers
Answer:
Step-by-step explanation:
x² - 3x - 1 = 0
a = 1, b = -3, c = -1
x₁ = (3 + sqrt(-3² - 4(1(-1))))/(2(1))
x₁ = (3 + sqrt(9 + 4))/2
x₁ = (3 + sqrt(13))/2
x₁ = 3.302...
x₂ = (3 - sqrt(-3² - 4(1(-1))))/(2(1))
x₂ = (3 - sqrt(9 + 4))/2
x₂ = (3 - sqrt(13))/2
x₂ = -0.302...
subtraction of fractions 7 1/4 - 2 1/8 =
Answers
Answer:
Exact form: 41/8
Decimal: 5.125
Mixed Fraction: 5 1/8
Answer:
5 1/2
Step-by-step explanation:
I'm not sure if I'm right but I did 7-2
and 1/4 is 1/2 of an 8th. You might have to wait for someone who is fully sure about the question
A warehouse worker uses a forklift to move boxes that weigh either 45 pounds or 70 pounds each. Let x be the number of 45-pound boxes and y be the number of 70-pound boxes. The forklift can carry up to either 60 boxes or a weight of 3000 pounds.
The total number of boxes that a forklift can carry is???
The total weight that the forklift can carry is ______ 3000 pounds.
Greater than, Less than, or Equal to
Write an inequality that models the number of boxes the forklift can carry. The inequality should contain x, y, and an inequality sign.
Write an inequality that models the amount of weight the forklift can carry. The inequality should contain x, y, and an inequality sign.
Answers
Part a: total number of boxes carried by the forklift = 60.
Part b: Total weight carried by forklift is "less than" 3000 pounds.
Explain about the inequality equation?Both mathematical phrases, equations and inequalities, are created by connecting two expressions. The equal sign (=) indicates that two expressions in an equation are believed to be equivalent. The symbols >, <, ≤ or ≥. or indicate that the two expressions in an inequality are not always equal.
Given data:
x - number of 45-pound boxesy - number of 70-pound boxes.maximum weight 3000 pounds.Maximum number = 60.in equality formed are:
x + y ≤ 60 number .....eq1
45x + 70y ≤ 3000 pounds ...eq 2
Part a: total number of boxes carried by the forklift = 60.
Part b: Total weight carried by forklift is "less than" 3000 pounds.
Part c: inequality for number of boxes carried by the forklift.
From eq 1, x + y ≤ 60
Part d: inequality for amount of weight carried by the forklift.
From eq 2; x + y ≤ 60
Know more about the inequality
https://brainly.com/question/24372553
#SPJ1
The box and whisker plot shows the recent test scores from WYVA Summit Math 6 class.
A. What is the interquartile range in a box-and-whisker plot?
B. What percent of the students got 80% or higher, which would be a B?
C. Write about Math: Using the interquartile range, explain how well the math class did on this test.

Answers
a. It represents the spread of the middle 50% of the data.
b. At least 50% of the students scored between 80 and 86.
c. Overall, we can say that the Math 6 class had a range of test scores, with some students performing very well and others performing less well.
What is interquartile range?How evenly distributed the middle 50% of the data is is determined by the interquartile range. In order to calculate it, the first quartile is subtracted from the third quartile.
A. The interquartile range (IQR) in a box-and-whisker plot is the distance between the first quartile (Q1) and the third quartile (Q3) of the data. It represents the spread of the middle 50% of the data.
B. To determine what percent of the students got 80% or higher, we need to find the upper fence, which is defined as 1.5 times the IQR above Q3. From the box-and-whisker plot, we can see that Q3 is approximately 86 and Q1 is approximately 71. Therefore, the IQR is 86 - 71 = 15. The upper fence is 1.5 * 15 + 86 = 108.5.
Looking at the plot, we can see that there are no data points above 100, so we can safely assume that no students scored above 100%. The highest score is 94, which is within the whiskers of the box-and-whisker plot. Therefore, we know that the percent of students who scored 80% or higher is between the percent of students who scored 80% or higher and the percent of students who scored 94% or higher.
From the plot, we can see that the median is approximately 80 and the third quartile (Q3) is approximately 86. This means that at least 50% of the students scored between 80 and 86. Additionally, we know that the maximum score is 94, so we can say that at least some students scored higher than 86. However, we don't know how many students scored between 86 and 94.
C. Based on the interquartile range, we can say that the middle 50% of the students scored between approximately 71 and 86. This suggests that there is a significant amount of variability in the test scores, as the range is quite wide. Additionally, we know that at least some students scored above 86, but we don't have enough information to determine how many or how high their scores were. Overall, we can say that the Math 6 class had a range of test scores, with some students performing very well and others performing less well.
To know more about interquartile range visit :-
https://brainly.com/question/29165499
#SPJ1
Last year mrs Bowen's read 289 books. Mrs Jackson's class read 315 book. About how many books did both classes read?
Answers
Answer:
604
Step-by-step explanation:
add them together using collum method
Does the equation below represent a
direct proportion? If yes, identify
the constant of proportionality.
х = 6у
A. No
B. Yes, 36
C. Yes, -6
D. Yes, 1/6
Answers
Step-by-step explanation:
The given equation is :
x = 6y ...(1)
Here,
x and y are variables and 6 is a constant number
It means,
x and y are related directly to each other i.e.
x ∝ y
or
x = ky .....(2)
Comparing equation (1) and (2)
k = 6
Hence, yes they are in direct proportion and the value of constant of proportionality is 6.
Answer:
yes / 1/6
Step-by-step explanation:
Calcular los 3/5 de los 2/3 de las 3/4 de 560
Answers
For the fractions, the calculation of 3/5 of 2/3 of 3/4 of 560 is equal to 168.
How to solve fractions?To calculate 3/5 of 2/3 of 3/4 of 560, break it down step by step:
Step 1: Calculate 3/4 of 560:
3/4 × 560 = (3 × 560) / 4 = 1680 / 4 = 420
Step 2: Calculate 2/3 of the result from Step 1:
2/3 × 420 = (2 × 420) / 3 = 840 / 3 = 280
Step 3: Calculate 3/5 of the result from Step 2:
3/5 × 280 = (3 × 280) / 5 = 840 / 5 = 168
Therefore, 3/5 of 2/3 of 3/4 of 560 is equal to 168.
Find out more on fractions here: https://brainly.com/question/78672
#SPJ1
How to calculate volume of a rectangular prism
Answers
Calculating the volume of a rectangular prism is a simple process that involves multiplying the length, width, and height.
Calculating the volume of a rectangular prism is a straightforward process. A rectangular prism is a three-dimensional shape that has a length, width, and height. To find its volume, you simply multiply the length by the width by the height. The formula for calculating the volume of a rectangular prism is:
Volume = length x width x height
For example, if a rectangular prism has a length of 5 cm, a width of 4 cm, and a height of 3 cm, its volume would be:
Volume = 5 cm x 4 cm x 3 cm
Volume = 60 cubic centimeters (cm³)
It's important to ensure that all measurements are in the same unit before calculating the volume. For instance, if the length is in meters and the width and height are in centimeters, you would need to convert the length to centimeters to ensure that all measurements are in the same unit before calculating the volume.
In conclusion, calculating the volume of a rectangular prism is a simple process that involves multiplying the length, width, and height. This formula can be used for any rectangular prism regardless of its size or shape.
For more questions on volume
https://brainly.com/question/28298028
#SPJ11
alex has 3 bags with the same amount of marbles in them, totaling 12 marbles. kirian has 3 bags with the same amount in them totaling 18 marbles. how many more marbles does kirian have in each bag?
Answers
Answer:
1944
Step-by-step explanation:
3*12=36*3=918*18=1944
Anu was checking her emails she casually told her friend siting next to her the ratio of unread emails in my inbox is 4:1 The total number of emails is 120 what is the number of unread emails in her inbox
Answers
In a case whereby Anu was checking her emails and she casually told her friend siting next to her the ratio of unread emails in my inbox is ratio 4:1 where the total number of emails is 120 then the number of unread emails in her inbox is 96mails.
How can the unread mails be calculated?The concept that will be used here is ratio. An ordered pair of numbers a and b, represented as a / b, is a ratio if b is not equal to 0. A proportion is an equation that sets two ratios at the same value. For instance, you could express the ratio as follows: 1: 3 if there is 1 boy and 3 girls (for every one boy there are 3 girls)
The total mails in her box is 120
The we can represent the unread mails as 4x and read mails be 1x
This can be expressed as :
(4x+1x)=120mails
5x=120mails
x=120/5
x=24
This implies that the uread mails(4×24)
=96mails
Then the number of the read mail =(1×24)=24mails
Learn more about emails at:
https://brainly.com/question/20731943
#SPJ1
Développer et réduire (3 − 2)² + (7 + 5)(3 − 2)
Answers
\((3-2)^2+(7+5)(3-2)=(3-2)(3-2)+(7+5)(3-2)=(3-2)(3-2+7+5)=1*13=13\)
What is the discriminant of the quadratic equation -x^2+6x-6=0
Answers
The discriminant of the quadratic-equation -x^2 + 6x - 6 = 0 is 60.
The discriminant of a quadratic equation of the form ax^2 + bx + c = 0 is given by the expression Δ = b^2 - 4ac.
In the given quadratic equation -x^2 + 6x - 6 = 0, we can identify that a = -1, b = 6, and c = -6.
Substituting these values into the discriminant formula, we have:
Δ = (6)^2 - 4(-1)(-6)
The discriminant plays a crucial role in determining the nature of the solutions of a quadratic equation. If the discriminant is positive (Δ > 0), then the equation has two distinct real solutions. If the discriminant is zero (Δ = 0), then the equation has one real solution (also known as a double root). If the discriminant is negative (Δ < 0), then the equation has no real solutions, but it may have complex solutions involving imaginary numbers.
for more such questions on quadratic-equation
https://brainly.com/question/1214333
#SPJ8
omplete the paragraph proof.
Given: and are right angles
Line segment A B is-congruent-to line segment B C Line segment B C is-congruent-to line segment A C
Prove: Line A R bisects Angle B A C
Triangles A B R and R C A share side R A. A line is drawn from point B to point C and intersects side A R at point P.
It is given that and are right angles, and . Since they contain right angles, ΔABR and ΔACR are right triangles. The right triangles share hypotenuse , and reflexive property justifies that . Since and , the transitive property justifies . Now, the hypotenuse and leg of right ΔABR is congruent to the hypotenuse and the leg of right ΔACR, so by the HL congruence postulate. Therefore, ________ by CPCTC, and bisects by the definition of bisector.
Answers
The BR is the perpendicular bisector of AC by CPCTC (corresponding parts of congruent triangles are congruent).
Based on the given information that angles ABR and ACR are right angles, and AB = AC, we can conclude that triangles ABR and ACR are right triangles.
Using the shared hypotenuse AR and the reflexive property, we can determine that side AB is congruent to side AC.
With this information, the transitive property allows us to conclude that angle BAR is congruent to angle CAR. Next, using the HL congruence postulate, we can prove that triangle ABR is congruent to triangle ACR.
This means that side BR is congruent to side CR, and angle BAC is bisected by line segment BR by the definition of bisector.
To learn more about : perpendicular
https://brainly.com/question/28063031
#SPJ8