Answers
Answer:
B.
Step-by-step explanation:
Hope dis helps! :) I know for a fact its correct.
Answer:
The Correct answer for this question is B.
I hope this helps you answer this question.
:)
Related Questions
A company makes parts for a medical machine. The lengths of the parts must be within certain limits or they will be rejected.
A large number of parts were measured and the mean and standard deviation were calculated as 3.1 m and 0.005 m respectively.
Assuming this data is normally distributed and 99.7% of the parts were accepted, what are the limits?
Answers
The required limit of 99.7%, normally distributed, parts that is accepted is (3.085, 3115).
Given that,
In the question sample mean ( M ) is 3.1 m, the standard deviation ( σ ) is 0.005 m, and the percentage of parts accepted is 99.7%.
Statistic is defined as the mathematical analysis dealing with relations between comprehensive data.
Applying Empirical Rule,
Here, 99.7% of data followed a normal distribution,
Distribution along the mean or limits be;
Distribution or limit = M ± 3σ
Limit = 3.1 ± (3 . 0.005)
Limit = 3.1 ± 0.015
Limit = {(3.1 - 0.015), (3 + 0.015)}
Limit = {3.085, 3.115}
Thus, the required limit of 99.7%, normally distributed, parts that is accepted is (3.085, 3115).
Learn more about Statistics here:
https://brainly.com/question/23091366
#SPJ1
Mrs Sogiba is catering for her son's birthday party. she has invited some of her son's friends to the party. the number of friends is a composite multiple of her son's age on his birthday. she has baked 48 cupcakes and each child will receive exactly the same number of cupcakes. use your knowledge of multiples and factors to find out how old her son will be on his birthday. (this is not his first birthday)hint- the trick to this question is to remember that the birthday boy will also get cupcakes... list all the factors of 48 ( because the children will all receive the same amount of cupcakes) then try to find a factor that gives a number that could be a a multiple of the boys age when you subtract 1 from the factor remember that the boy is turning at least 2 years old
Answers
Explanation
Mrs Sogiba has baked 48 cupcakes and each child will receive exactly the same number of cupcakes.
\(Factors\text{ of 48 = }1,2,4,6,8,12,24,48\)Recall composite factors are factors of a number that are not prime. Therefore the composite factors from the above are;
\(\text{Composite factors = }48,24,12,8,6,4\)If we subtract 1 from the composite factors, the possible values becomes
\(\text{Values}=\text{ 47,23,11,7,5,3}\)From the above, we can have
\(\begin{gathered} Friends=3\times4=12 \\ numberofcupcakes=12\times4=48 \end{gathered}\)Therefore,
Answer: Age of son can be 3 Years
Need help on finding g .

Answers
The numeric values for this problem are given as follows:
g(-1) = -2.g(2) = 0.g(3) = 0.5.How to obtain the numeric values of the function?The function in this problem is a piecewise function, meaning that it has different definitions based on the input x of the function.
For x between -2 and 2, the function is defined as follows:
g(x) = -(x - 1)² + 2.
Hence the numeric value at x = -1 is given as follows:
g(-1) = -(-1 - 1)² + 2 = -4 + 2 = -2.
For x at x = 2 and greater, the function is given as follows:
g(x) = 0.5x - 1.
Hence the numeric values at x = 2 and x = 3 are given as follows:
g(2) = 0.5(2) - 1 = 0.g(3) = 0.5(3) - 1 = 0.5.A similar problem, also featuring numeric values of a function, is given at brainly.com/question/28367050
#SPJ1
Someone please help and show work

Answers
Mean - this is the average. Add up the numbers and divide by the count of the numbers in the data set.
11+13+14+16+17+18+20+20+21+24+25+29 = 228
There are 12 numbers, so divide by 12.
228/12 = 19. The mean is 19.
Median - - - this is the MIDDLE number. Your data is already in numerical order (hooray!) so there are 12 numbers. Since it's even, we'll take the average of the 2 middle numbers. The 6th number is 18 and the 7th number is 20. The average of these is 19. So the median is 19.
(Side note: yes, median and mean can be the same.)
Mode - - - this is repeat/most common numbers! 20 repeats. 20 is the mode.
Range - - - biggest number is 29, littlest is 11. The range is 29-11 = 18.
The numbers of beads on 500 handcrafted bead necklaces follow a normal distribution whose mean is 24 beads and standard deviation is 4 beads. Which sentence most closely summarizes the data?
Answers
About 80 necklaces have more than 28 beads. Then the correct option is C.
What is a normal distribution?The Gaussian Distribution is another name for it. The most significant continuous probability distribution is this one. Because the curve resembles a bell, it is also known as a bell curve.
The numbers of beads on 500 handcrafted bead necklaces follow a normal distribution whose mean is 24 beads and the standard deviation is 4 beads.
P(x > 28) = P(x - 24 / 4 > 28 - 24 / 4)
P(x > 28) = P(x - 24 / 4 > 1)
P(x > 28) = 1 - ∅1
P(x > 28) = 1 - 0.8413
P(x > 28) = 0.1587
Multiply both sides by 500, then we have
500 P(x > 28) = 0.1587 × 500
500 P(x > 28) = 79.35
500 P(x > 28) ≈ 80
About 80 necklaces have more than 28 beads. Then the correct option is C.
More about the normal distribution link is given below.
https://brainly.com/question/12421652
#SPJ1
The missing options are given below.
A. About 24 devices have more than 28 beads.
B. About 48 necklaces have more than 28 beads.
C. About 80 necklaces have more than 28 beads.
D. About 96 necklaces have more than 28 beads.
Find the inverse of A = 9, -2 -10, 7 , if it exists.
Answers
The inverse of matrix A, if it exists, is:
A^(-1) = [7/43, 2/43; 10/43, 9/43]
To find the inverse of a matrix A, we need to determine if the matrix is invertible by calculating its determinant. If the determinant is non-zero, then the matrix has an inverse.
Given the matrix A = [9, -2; -10, 7], we can calculate its determinant as follows:
det(A) = (9 * 7) - (-2 * -10)
= 63 - 20
= 43
Since the determinant is non-zero (43 ≠ 0), we can proceed to find the inverse of matrix A.
The formula to calculate the inverse of a 2x2 matrix is:
A^(-1) = (1/det(A)) * [d, -b; -c, a]
Plugging in the values from matrix A and the determinant, we have:
A^(-1) = (1/43) * [7, 2; 10, 9]
Simplifying further, we get:
A^(-1) = [7/43, 2/43; 10/43, 9/43].
For more such questions on Inverse of matrix:
https://brainly.com/question/27924478
#SPJ8
Please help solve for a in the equation in the photo

Answers
\(\huge\bf Question:—\)
\( \sf \longmapsto \: g=a(4− {d}^{2} )\)
\(\huge\bf Solution:—\)
\( \underline{\bf \: Flip \: the \: equation:—}\)
\( \sf \longmapsto \: −a {d}^{2} +4a=g\)
\( \underline{\bf \: Factor \: out \: variable \: (a):—}\)
\( \sf \longmapsto \: a(− {d}^{2} +4)=g\)
\(\underline{ \bf \: Divide \: both \: sides \: by -d^2+4 :—} \)
\(\sf \longmapsto \: \dfrac{a( - {d}^{2} + 4) }{ { - d ^2+ 4}^{} } = \dfrac{g}{{ - d ^2+ 4}^{}} \)
\(\sf \longmapsto \:1 a = \dfrac{g}{{ - d^2 + 4}^{}} \)
\(\underline{\bf Answer:—}\)
\(\boxed{ \bf \: a = \dfrac{g}{ - d^2 + {4}^{} } }\)
Answer:
\(\boxed{\boxed{\sf a=\cfrac{G}{4-d^2} }}\)
Step-by-step explanation:
\(\sf G=a(4-d^2)\)
Use the Distributive Property to multiply a by (4-d^2):
\(\sf G=4a-ad^2\)
Now, we'll swap sides so that all variable terms are on the left hand side.
\(\sf 4a-ad^2=G\)
Combine like terms:
\(\sf (4-d^2)\:a =G\)
Divide both sides by 4-d^2:
\(\sf \cfrac{(4-d^2)a}{4-d^2} =\cfrac{G}{4-d^2}\)
Dividing by 4-d^2 undoes the multiplication by 4-d^2.
\(\sf a=\cfrac{G}{4-d^2}\)
_______________________________________
Simplify each side of 4a+ 5a-2=5+3-1
Answers
Answer:
9a-2=7
Step-by-step explanation:
4a+ 5a-2=5+3-1
To simplify each side, combine like terms.
4a+5a = 9a
5+3-1 = 7
The equation becomes:
9a-2=7
The temperature outside changed from 66°F to 42°F over a period of eight days. If the temperature changed by the same amount each day, what was the daily temperature change?
Answers
The area of the parallelogram is 17.6 cm 2 . What is the length of the base?
Answers
Answer:
The length of the base is 4.4 cm
area of parallelogram: base x height =
1) first you do 17.6=4 x h, which gives you 17.6/4
Answer:
area of parallelogram: base x height = 17.6 cm sq
}4 x h = 17.6
⇒h = 17.6/4
⇒h= 4.4 cm
Step-by-step explanation:
Hope it helps
2/5x - 1/3(2x - 4) = 1/5 (2 - 8x)
help please!!
Answers
Find the slope of the line contains P1 and P2
Interpret this slope
P1=(-1,3 and p2 =(5,-1)
Answers
Answer:
\(m = -\frac{2}{3}\)
Step-by-step explanation:
Given
\(P_1 = (-1,3)\)
\(P_2 = (5,-1)\)
Required
Determine and interpret slope
Slope is calculated using:
\(m = \frac{y_2 - y_1}{x_2 - x_1}\)
Where
\((x_1,y_1) = (-1,3)\)
\((x_2,y_2) = (5,-1)\)
\(m = \frac{y_2 - y_1}{x_2 - x_1}\) becomes
\(m = \frac{-1 - 3}{5 - (-1)}\)
\(m = \frac{-1 - 3}{5 +1}\)
\(m = \frac{-4}{6}\)
\(m = -\frac{2}{3}\)
The above slope is negative and it implies that x increases when y decreases and vice versa.
What the meaning of statement this?

Answers
The axiom of regularity is a set theory principle which states that every non-empty set C contains an element that is disjoint from C.
Axiom of RegularityThe set theory concept rules that for every non-empty set C there is an element x of C such that x does not intersect C. The regularity axiom aims to establish that no non-empty set will have itself as an element.
The principle which is also called the axiom of foundation is a fundamental concept in set theory and credited to Zermelo–Fraenkel.
Learn more about set theory ; https://brainly.com/question/13458417
#SPJ1
A square garden has a length of (x+3) ft and a width of (x+2) ft. what is the perimeter and area of the garden?
Answers
Answer:
Perimeter:\(4x+10\) feet
Area:\(x^{2}+5x+6\) feet
Step-by-step explanation:
The perimeter is equal to 2*width +2*length. The width is x+2 and the length is x+3, therefore the perimeter is equal to 2x+4+2x+6 which equals 4x+10.
The area is equal to width*length
(x+3)(x+2)=\(x^{2}+2x+3x+6=x^{2}+5x+6\)
A table of values of a linear function is shown below. Find the output when the input is N. Type your answer in the space provide

Answers
Answer:
\( -3n - 7 \)
Step-by-step explanation:
Considering the linear function represented in the table above, to find what output an input "n" would give, we need to first find an equation that defines the linear function.
Using the slope-intercept formula, y = mx + b, let's find the equation.
Where,
m = the increase in output ÷ increase in input = \( \frac{-13 - (-10)}{2 - 1} \)
\( m = \frac{-13 + 10}{1} \)
\( m = \frac{-3}{1} \)
\( m = -3 \)
Using any if the given pairs, i.e., (1, -10), plug in the values as x and y in the equation formula to solve for b, which is the y-intercept
\( y = mx + b \)
\( -10 = -3(1) + b \)
\( -10 = -3 + b \)
Add 3 to both sides:
\( -10 + 3 = -3 + b + 3 \)
\( -7 = b \)
\( b = -7 \)
The equation of the given linear function can be written as:
\( y = -3x - 7 \)
Or
\( f(x) = -3x - 7 \)
Therefore, if the input is n, the output would be:
\( f(n) = -3n - 7 \)
Ayuda operaciones y respuesta es para ahora

Answers
The perimeter of the given window is 48 centimeter.
From the given figure,
Perimeter of window = 2(Length+Breadth)
= 2(10+14)
= 2×24
= 48 centimeter
Perimeter of house = 2(Length+Breadth)
= 2(37+35)
= 2×72
= 144 centimeter
Perimeter of roof = 2(Length+Breadth)
= 2(37+5)
= 2×42
= 84 centimeter
Therefore, the perimeter of the given window is 48 centimeter.
To learn more about the perimeter visit:
https://brainly.com/question/6465134.
#SPJ1
The perimeter of a rectangle is 332cm and the width is 76cm. Find the rectangle’s length
Answers
solution: 332 - 76 - 76 = 180
180 ÷ 2 = 90
What is the slope of the line that passes through the points (9, 5)(9,5) and (21, 1) ?(21,1)? Write your answer in simplest form.
Answers
Answer:
i know this but do not lol
Step-by-step explanation:
Answer:
did u mean to put (9,5) and (21,1) in there twice? but if so ur answer is m= -1/3
TRY USING SYMBOLAB I USE ALL THE TIME
what does 2x-10=4x equal
Answers
Answer:
x = -5
Step-by-step explanation:
Answer:
x = -5
Step-by-step explanation:
You want the solution to the equation 2x -10 = 4x.
SolutionSubtracting 2x from both sides gives ...
-10 = 2x
Dividing both sides by 2 gives ...
-5 = x
The solution is x = -5.
__
Additional comment
When all of the coefficients have a common factor, sometimes we like to divide the equation by that factor. Here, all of the coefficients are even, so we can start by dividing the equation by 2:
x -5 =2x
Now subtracting x gives the solution:
-5 = x
It still takes 2 steps, so the approach you take will be the one you're most comfortable with.
<95141404393>
In one part of a rainforest 3/5 of the frogs are poisonous. what fraction of the frogs are not poisonous?
Answers
Then 1 - 3/5 = 2/5. This means that 2/5 of the frogs in that particular part of the rainforest are not poisonous. This fraction can also be expressed as 40/100 or 0.4 in decimal form.
In the given scenario, we know that 3/5 of the frogs in a particular part of the rainforest are poisonous. This means that the remaining fraction of the frogs are not poisonous.
To find this fraction, we need to subtract 3/5 from 1 (since the sum of the fractions of poisonous and non-poisonous frogs is equal to 1).
It's important to note that just because a frog is not poisonous, it doesn't mean it's safe to touch or handle them. It's always best to admire these beautiful creatures from a safe distance and leave them alone in their natural habitat.
To learn more about : fraction
https://brainly.com/question/17220365
#SPJ8
HELP IM IN K12 AND THERS MORE OF THESE

Answers
1a and b. Plz show ALL STEPS like LITERALLY ALL STEPS
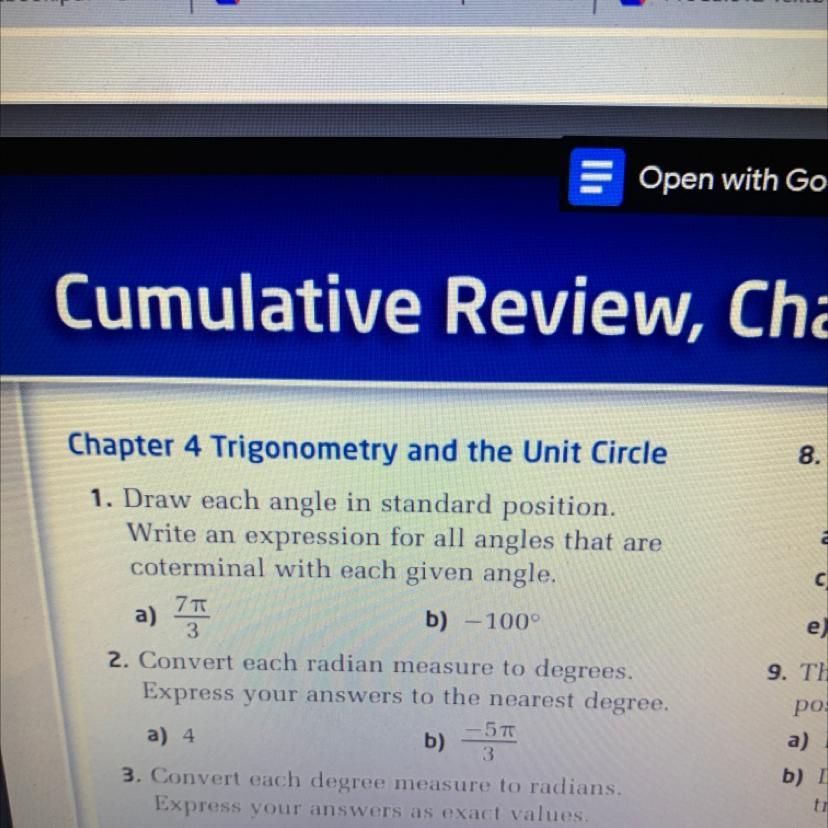
Answers
Answer:
See step by step
Step-by-step explanation:
1a.
\( \frac{7\pi}{3} \)
Coterminal Angles difference or a full revolution or 2 pi. so it standard position will be
\( \frac{7\pi}{3} - \frac{6\pi}{3} = \frac{\pi}{3} \)
The expression will be
\( \frac{\pi}{3} + 2\pi \times n\)
where n is the interger number of revolutions.
1b. Instead using radians, we will be using degrees.
Coterminal Angles difference will be 360 degrees. so it standard position within the unit circle will be
\( - 100 + 360 = 260\)
The expression is
\( - 100 + 360 \times n\)
where n is the interger number of revolutions.
If the following data were transformed and points with the coordinates
(x, log(y)) were plotted, what points would be plotted? Round log(y) to three
decimal places.
X
1
2
3
y
12
83
580

Answers
If the data were transformed and points with the coordinates
(x, log(y)) were plotted then the points (1, 1.079), (2, 1.919), (3, 2.763) were plotted.
To plot the points with the coordinates (x, log(y)), we need to take the logarithm of the y-values.
Let's calculate the logarithms for the given data:
x y log(y)
1 12 log(12) = 1.079
2 83 log(83) = 1.919
3 580 log(580) = 2.763
Therefore, the points that would be plotted are (1, 1.079), (2, 1.919), (3, 2.763)
To learn more on Logarithms click:
https://brainly.com/question/30226560
#SPJ1
The pet shop has 6,157 dog treats. They packed the treats into bags with 7 pieces in each bag. Any treats that did not fit into a bag of 7 were given to Groomer to use to reward animals getting bathed. How many bags of treats did they fill? How many treats were given to the groomer?
Answers
They filled bags that total 879 and the treats that did not fit are 4
What is unitary method?The unitary method is a technique for solving a problem by first finding the value of a single unit, and then finding the necessary value by multiplying the single unit value.
Given here, total treats = 6157, and group them in bags with 7 each
now, we can write 6157 = 879×7+4
thus, on dividing 6157 by 7 we get the remainder as 4 and the quotient as 879
Hence, the bags of treats they filled is 879, and 4 treats were given to the groomer
Learn more about the quotient and remainders here:
https://brainly.com/question/17385796
#SPJ1
In a right-angled triangle the ratio of the two smaller angles is 3:2. Find the sizes of each of the angles.
Answers
Answer:
36° , 54° , 90°
Step-by-step explanation:
since the triangle is right then one angle is 90°
the ratio of the smaller angles = 3 : 2 = 3x : 2x ( x is a multiplier )
the sum of the 3 angles in the triangle is 180° , that is
3x + 2x + 90 = 180
5x + 90 = 180 ( subtract 90 from both sides )
5x = 90 ( divide both sides by 5 )
x = 18
Then
3x = 3 × 18 = 54°
2x = 2 × 18 = 36°
the 3 angles measure 36° , 54° , 90°
Help meeeeeeeeeeeeeeeeeeee

Answers
Answer:
I believe it is y=1x or y=x
Answer:
14
Step-by-step explanation:
The constant of proportionality is the y number when x is 1. Look on the bottom of the graph. Find 1, so up to the line and then across left to the y axis. you will be at 14. This means that every time the x increases by 1, the increases by 14
Draw the net and calculate the surface area .

Answers
Hello!
surface area
= 2(4 x 2) + 2(12 x 4) + 2(12 x 2)
= 160cm²
What should be done to x^2 -8x to create a perfect square?
Answers
Step 1:
Write the expression
\(x^2\text{ - 8x}\)Step 2:
\(\begin{gathered} To\text{ make the expression a p}\operatorname{erf}ect\text{ square, find c from} \\ b^2\text{ = 4ac} \end{gathered}\)Step 3:
a = 1 , b = -8 , c = ?
Next, find c
\(\begin{gathered} b^2\text{ = 4ac} \\ (-8)^2\text{ = 4 }\times\text{ 1 }\times\text{ c} \\ 64\text{ = 4c} \\ c\text{ = }\frac{64}{4} \\ c\text{ = 16} \end{gathered}\)Final answer
\(\begin{gathered} To\text{ make } \\ x^2\text{ - 8x a p}\operatorname{erf}ect\text{ square , add 16} \\ x^2\text{ - 8x + 16} \end{gathered}\)Answer = 16
Find the 70th term of the arithmetic sequence -26, -19, -12
Answers
Answer:
457
Step-by-step explanation:
The general term of an arithmetic sequence is given by ...
an = a1 +d(n -1)
where a1 is the first term (-26), and d is the common difference (7).
The 70th term of your sequence can be found by putting the numbers into this formula:
a70 = -26 +7(70 -1) = -26 +483
a70 = 457
The 70th term of the sequence is 457.
Use the product-to-sum identities to rewrite the following expression as a sum or difference.
2sin(2x)sin(2x)
Answers
The sum form of the trigonometric function 2 · sin 2x · sin 2x by product-to-sum formula is 1 - cos 4x.
How to transform a product of trigonometric functions into a sum of trigonometric functions
Herein we find the definition of a trigonometric function defined as a product of trigonometric function, this can be transformed into a sum of trigonometric functions by means of the following product-to-sum formula:
sin α · sin β = [cos (α - β) - cos (α + β)] / 2
First, write the trigonometric function defined in the statement:
2 · sin 2x · sin 2x
Second, use the product-to-sum formula by considering α = β = 2 · x:
2 · [[cos (2x - 2x) - cos (2x + 2x)] / 2]
cos 0 - cos 4x
1 - cos 4x
Third, write the resulting expression:
2 · sin 2x · sin 2x = 1 - cos 4x
To learn more on trigonometric formulas: https://brainly.com/question/19560372
#SPJ1

