Answers
Answer:
49
Step-by-step explanation:
i see the other answer is absolutely useless
Marble:Stone
6 : 7
42 : 49
therefore there are 49 stones
Answer:
49
Step-by-step explanation:
42 ÷ 6 is 6
7 x 7 is 49
so its 49
Related Questions
Pls help i will award brainliest!!!!!!


Answers
Answer: x= -2
Step-by-step explanation:
Let's solve your equation step-by-step.
3−2x=x+9
Step 1: Simplify both sides of the equation.
3−2x=x+9
3+−2x=x+9
−2x+3=x+9
Step 2: Subtract x from both sides.
−2x+3−x=x+9−x
−3x+3=9
Step 3: Subtract 3 from both sides.
−3x+3−3=9−3
−3x=6
Step 4: Divide both sides by -3.
−3x/−3 = 6/−3
x=−2
what is the answer to 0.15 = y - 0.45
Answers
Answer:
0.6
Step-by-step explanation:
Help me please with my IXL GEOMETRY
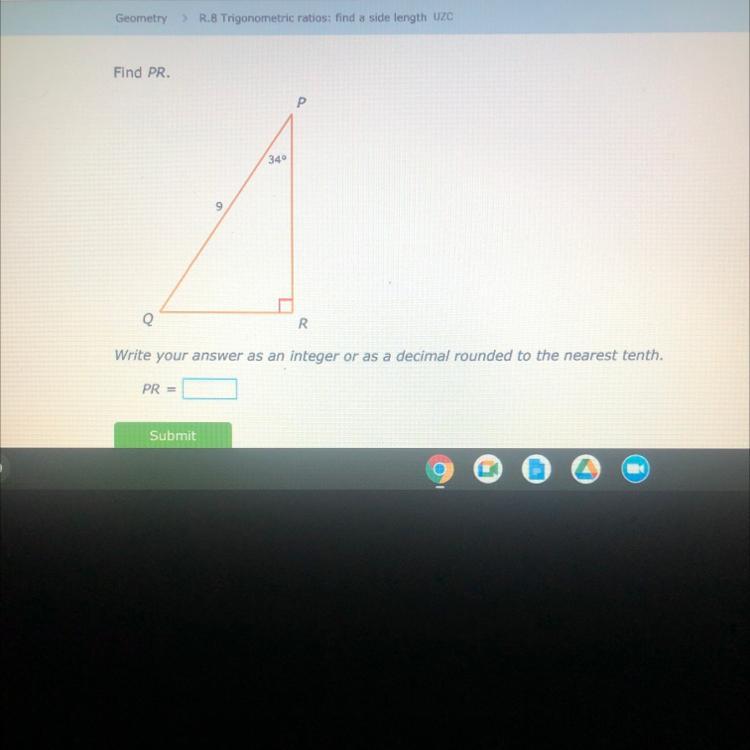
Answers
Answer:
7.5
Step-by-step explanation:
hey hope this helps and is right

A payday loan company charges a $90 fee for a $500 payday loan that will be repaid in 16 days.
Treating the fee as interest paid, what is the equivalent annual interest rate?
Answers
Answer:
Kindly check explanation
Step-by-step explanation:
Given :
Interest amount paid on loan = $90
Principal value, amount borrowed = $500
Period, t = 16 days
The equivalent annual interest :
Using the simple interest formula :
simple interest = principal * rate * time
Using, days of year = 365
Plugging in the values into the formula :
90 = 500 * rate * (16/365)
90 = 500 * rate * 0.0438356
90 = 21.917808 * rate
Rate = 90 / 21.917808
Rate = 4.10 = 4.10 * 100% = 410%
If days of year = 360 is used :
90 = 500 * rate * (16/360)
Rate = 90 / 22.222
Rate = 4.05 = 4.105 * 100% = 405%
At a concession stand, five hot dog(s) and four hamburger(s) cost $16.75; four hot dog(s) and five hamburger(s) cost $17.00. Find the cost of one hot dog and the cost of one hamburger.
Answers
Step-by-step explanation:
Let x and y denote the cost of one hot dog and the cost of one hamburger.
ATQ,
Five hot dog(s) and four hamburger(s) cost $16.75 and four hot dog(s) and five hamburger(s) cost $17.00
So,
5x+4y = 16.75 ....(1)
4x + 5y = 17 ....(2)
Multiply equation (1) by 4 and equation (2) by 5.
20x+16y = 67 ....(3)
20x+25y= 85 ....(4)
Subtract equation (3) and (4).
20x+16y-(20x+25y) = 67-85
16y-25y = -18
-9y = -18
y = 2
Put the value of y in equation (2).
4x + 10 = 17
4x = 7
x = 1.75
So, the cost of one hot dog is $1.75 and that of cost of one hamburger is $2.
Answer this question please

Answers
Shape P could have been transformed using a translation, rotation, reflection or a combination of these transformations.
What is tranformations?Transformation in maths is a way of changing the position, size or shape of a given object. It involves moving the object from one position to another. This can be done using a combination of translation, rotation, reflection and enlargement.
A translation is when a shape is moved in a straight line and all points are moved the same distance in the same direction. A rotation is when a shape is rotated around a fixed point and all points are moved the same angle. A reflection is when a shape is flipped over a line and all points are reversed on the other side of the line.
In the case of Shape P, since one point was invariant, the transformation must have been either a translation, rotation or a combination of both. A translation would have been impossible as all points are moved the same amount and direction, hence, the invariant point would have been moved. A rotation is possible as all points are moved the same angle, and the angle of rotation could be adjusted to keep the invariant point in the same place. A combination of both of these transformations could also have been used to keep one point invariant.
Overall, Shape P could have been transformed using a translation, rotation, reflection or a combination of these transformations. In this case, the transformation must have been either rotation or a combination of both translation and rotation. The angle of rotation or the combination of translation and rotation would have been adjusted to keep the invariant point in the same place.
For more questions related to enlargement
https://brainly.com/question/22973053
#SPJ9
Which is the correct trigonometric substitution for evaluating

Answers
The correct trigonometric substitution for evaluating integral ∫√(x² + 64) dx is option B. x = 8 tan θ.
How did we get the correct trigonometric substitution?To evaluate the integral ∫√(x² + 64) dx using trigonometric substitution, use the substitution x = 8 tan θ.
Let's go through the steps to see how this substitution leads us to the solution:
1. Substitute x = 8 tan θ.
This implies dx = 8 sec² θ dθ.
2. Substitute the expression for x and dx in the integral:
∫√(x² + 64) dx becomes ∫√((8 tan θ)² + 64) * 8 sec² θ dθ.
3. Simplify the expression:
∫√(64 tan² θ + 64) * 8 sec² θ dθ = ∫√(64(sec² θ - 1)) * 8 sec² θ dθ.
4. Further simplify:
∫√(64sec² θ - 64) * 8 sec² θ dθ = ∫√(64sec² θ) * 8 sec² θ dθ.
5. Simplify the expression inside the square root:
∫8sec θ * 8 sec² θ dθ = ∫64sec³ θ dθ.
6. Integrate with respect to θ:
∫64sec³ θ dθ = 64∫sec³ θ dθ.
Now, this integral can be evaluated using standard trigonometric integral identities or integration techniques. However, it's worth noting that the original integral did not involve the variable θ, so we would eventually need to convert the result back to x by substituting x = 8 tan θ.
The correct answer is B. x = 8 tan θ.
learn more about trigonometric substitution: https://brainly.com/question/17199316
#SPJ1
The table shows four transactions and the resulting account balance in a bank
account, except some numbers are missing. Fill in the missing numbers
transaction amount
account balance
transaction 1
360
360
transaction 2
-22.50
337.50
transaction 3
182.35
transaction 4
-41.40
Answers
The values that are missing from the transaction will be 155.15 and -223.75.
How to calculate the values on the transaction?It should be noted that a transaction simply means the agreement between the buyer and the seller to exchange a good or service.
In this situation, the table shows four transactions and the resulting account balance in a bank account, but some numbers are missing.
In this situation, it should be noted that the transaction amount in transaction 3 will be:
= 337.50 - 182.35
= 155.15
The amount in transaction 4 will be:
= -182.35 - 41.40
= - 223.75
Learn more about transactions on:
brainly.com/question/1016861
#SPJ1
tan(x-1) ( sin2x-2cos2x) = 2(1-2sinxcosx)
Answers
\(\huge\blue{\fbox{\tt{Solution:}}}\)
We can simplify the expression using trigonometric identities.
First, we can use the double angle formula for sine to write sin(2x) = 2sin(x)cos(x).
Next, we can use the double angle formula for cosine to write cos(2x) = cos^2(x) - sin^2(x) = 1 - 2sin^2(x). Rearranging this equation gives 2sin^2(x) - 2cos^2(x) = -cos(2x) + 1.
Substituting these identities into the original expression gives:
tan(x-1) ( sin2x-2cos2x) = tan(x-1) [2sin(x)cos(x) - 2(1 - 2sin^2(x))]
= 2tan(x-1)sin(x)cos(x) - 2tan(x-1) + 4tan(x-1)sin^2(x)
We can use the identity tan(x) = sin(x)/cos(x) to simplify this expression further:
2tan(x-1)sin(x)cos(x) - 2tan(x-1) + 4tan(x-1)sin^2(x)
= 2sin(x)cos(x)/(cos(x-1)) - 2sin(x)/(cos(x-1)) + 4sin^2(x)/(cos(x-1))
Multiplying both sides of the equation by cos(x-1) gives:
2sin(x)cos(x) - 2sin(x) + 4sin^2(x)cos(x-1) = 2(1-2sin(x)cos(x))
Expanding the left-hand side of the equation gives:
2sin(x)cos(x) - 2sin(x) + 4sin^2(x)cos(x) - 4sin^2(x) = 2 - 4sin(x)cos(x)
Simplifying this equation gives:
4sin^2(x) - 2sin(x) - 2 = 0
This is a quadratic equation in sin(x), which can be solved using the quadratic formula.
*
Write the equation in standard form.
y=5/3x+6
Your answer
Answers
Answer:
5x−3y=−18
Explanation:
\(y=\frac{5}{3} x+6\)
Multiply everything by 3.
\(3y=5x+18\\0=5x-3y+18\\5x-3y=-18\)
Subtract 3y and 18 from both sides.
Please help with the following question.

Answers
Answer:
Step-by-step explanation:
C
When do you use point slope form
Answers
Answer:
It can be used as a preference
Answer:
You use point-slope form when you know (or can determine) the slope and the coordinates of one point on the line.
Step-by-step explanation:
You use point-slope form when you know (or can determine) the slope and the coordinates of a point. So, either you are given the slope of the line and a point on the line, or you are given two points on the line and you use the points to determine the slope.

please help, I’ll give brainliest to anyone who gets it’s right:) if you send a link, I’ll report sorry! :(
The figures below show the populations of 25 cities randomly selected from the 200 largest
cities in each of two countries. Based on these samples, about how much larger is the
median population of China's 200 largest cities than the median population of India's 200
largest cities?

Answers
Answer:
600 000
Step-by-step explanation:
took the same test nav
A theater group made appearances in two cities. The hotel charge before tax in the second city was $1500 higher than in the first. The tax in the first city was 7.5%, and the tax in the second city was 5%. The total hotel tax paid for the two cities was $825. How much was the hotel charge in each city before tax?
Answers
The hotel charge in the first city before tax was $6000 and the hotel charge in the second city before tax was $7500.
Let x be the hotel charge before tax in the first city, and y be the hotel charge before tax in the second city. Then we have:
y = x + 1500 (the hotel charge before tax in the second city was $1500 higher than in the first)
0.075x + 0.05y = 825 (the total hotel tax paid for the two cities was $825)
We can use the first equation to solve for y in terms of x:
y = x + 1500
Then we can substitute this expression for y into the second equation:
0.075x + 0.05(x + 1500) = 825
Simplifying this equation, we get:
0.075x + 0.05x + 75 = 825
0.125x = 750
x = 6000
So the hotel charge before tax in the first city was $6000. Using the first equation, we can find the hotel charge before tax in the second city:
y = x + 1500
y = 6000 + 1500
y = 7500
So the hotel charge before tax in the second city was $7500.
Therefore, the answer is: The hotel charge in the first city before tax was $6000 and the hotel charge in the second city before tax was $7500.
For more questions on hotel charge
https://brainly.com/question/25569852
#SPJ11
A portfolio manager generates a 5% return in Year 1, a 12% return in Year 2, a negative 6% return in Year 3, and a return of 2% (nonannualized) in the first quarter in Year 4. The annualized return for the entire period is the closest to __________.
Answers
The annualized return for the entire period is the closest to 10.5%.
To calculate the annualized return for the entire period, we need to consider the returns for each year and the return in the first quarter of Year 4. Since the returns are given for each period, we can use the geometric mean to calculate the annualized return.
The formula for calculating the geometric mean return is:
Geometric Mean Return = [(1 + R1) * (1 + R2) * (1 + R3) * (1 + R4)]^(1/n) - 1
Where R1, R2, R3, and R4 are the returns for each respective period, and n is the number of periods.
Given the returns:
Year 1 return: 5% or 0.05
Year 2 return: 12% or 0.12
Year 3 return: -6% or -0.06
First quarter of Year 4 return: 2% or 0.02
Using the formula, we can calculate the annualized return:
Annualized Return = [(1 + 0.05) * (1 + 0.12) * (1 - 0.06) * (1 + 0.02)]^(1/3) - 1
Annualized Return = (1.05 * 1.12 * 0.94 * 1.02)^(1/3) - 1
Annualized Return = 1.121485^(1/3) - 1
Annualized Return ≈ 0.105 or 10.5%
Therefore, the annualized return for the entire period is approximately 10.5%.
For more question on return visit:
https://brainly.com/question/30761579
#SPJ8
Solve (x – 3)2 = 49. Select the values of x. –46 -4 10 52
Answers
Answer:10
Step-by-step explanation:
A cement mixture costs $33 a ton. It is composed of Grade A cement at $36 a ton and Grade B cement at
$24 a ton. How were these two cements mixed?
Answers
Converting to costs we get 36a + 24b = 33(a + b)
36a + 24b = 33a + 33b
36a - 33a = 33b - 24b
3a = 9b
a = 3b
This means the mixture contains 3 times as much of grade A than grade B
The ratio of grade A : grade B = 3 : 1
For example if we mixed 3 tons of A with 1 ton of B we would get 4 tons of mixture
The cost would be 3 x 36 + 1 x 24 = 108 + 24 = $132 for 4 tons = $33 per ton
Sam had 1 1-2 meters of rope. He cut off 5-8 meters and used it for the project. How much does Sam have left?
Answers
answer:
7/8 sam have left
Is anybody able to help me with math??? ANSWER ASAP
Answers
Answer:
I got you what do you need help with :)
Step-by-step explanation:
find the vertex and y intercept of the quadratic function, and use them to graph the function

Answers
Answer: 540 ft
Step-by-step explanation:
When given the equation in standard form y = ax² + bx + c,
the Axis of Symmetry can be found using the formula x = -b/(2a).
Plug that x-value into the given equation to find the y-value which represents the max (if "a" is negative) or the min (if "a" is positive)
y = -10x² + 160x - 100
↓ ↓ ↓
a= -10 b=160 c= -100
\(\text{AOS:}\quad x=\dfrac{-b}{2a}\quad =\dfrac{-(160)}{2(-10)}\quad =\dfrac{-160}{-20}\quad =8\)
Max: y = -10(8)² + 160(8) - 100
= -10(64) + 1280 - 100
= -640 + 1180
= 540
The table below is for a function A=f(d), which gives the amount of money A (in billions of dollars) in bills of denomination circulating in US currency in 2005. For example according to the table values below there were $60.2 billion worth of $50 bills in circulation.
Answers
Tables are used to show the relationship between related quantities. From the given table, the value of f(10) is 14.8
See attachment for the table of \(A = f(d)\)
To solve for f(10), we simply locate the value of A when d = 10
From the table
A = 14.8 when d = 10
This means that:
\(A =f(10) = 14.8\)
Hence:
\(f(10) = 14.8\)
Read more about functions at:
https://brainly.com/question/1446149

The answer to this problem please and thank you

Answers
Answer:
C
Step-by-step explanation:
The red dotted line we see is the asymptote, which is a line that the functions will never cross.
The asymptotes we see currently is:
x = -3
and
x = 2
We can find the vertical asymptotes using the denominator of the function since the x value that makes the denominator 0 is the asymptote. Since -3 and 2 is the asymptote, the denominator of the function will be:
(x-2) (x+3)
If we look at the answer choices, we can see that C is the only option with a denominator of (x-2)(x+3), so that is our answer.
Answer:
C
Step-by-step explanation:
there are 2 vertical asymptotes at x = - 3 and x = 2
then the factors on the denominator will be (x + 3) and (x - 2)
then
f(x) = \(\frac{1}{(x-2)(x+3)}\)
PLEASE ASAPPP I need thisss to pass

Answers
Answer:
c = 85+20d
c = 245
Step-by-step explanation:
Cost = initial fee + cost per day * number of days
cost = 85 + 20*d where d is the number of days
c = 85+20d
We need to rent for 8 days so d = 8
c = 85+ 20*8
c = 85 + 160
c =245
In Booneville, the library is 6 miles south of the courthouse and 7 miles west of the community swimming pool. If a bird flew directly from the courthouse to the library, then from the library to the swimming pool, and then from the swimming pool back to the courthouse, what would be the total distance flown?
Answers
The total distance flown by the bird directly from the courthouse to the library, then from the library to the swimming pool, and then from the swimming pool back to the courthouse is 13 + √85 miles
What is distance:Generally, distance is a scalar quantity . This means it has only magnitude but no direction.
Distance describes how much ground an object covers on motion.
Therefore, the total distance the bird flew is how much ground it covered during motion.
The library is 6 miles south of the courthouse and 7 miles west of the community swimming pool.
Distance from court house to the library = 6 miles
Distance from library to the swimming pool = 7 miles
we use Pythagoras's theorem to find the distance from the swimming pool back to the courthouse. Therefore
c² = a² + b²Distance from swimming pool to the court house = 7² + 6² = 49 + 36 = √85
Total distance travelled = 6 + 7 + √85 = 13 + √85 miles
learn more on distance: https://brainly.com/question/24981044?referrer=searchResults
Which system of linear inequalities has the point (3, -2) in its solution set?
y < -3; y ≤ 2/3x - 4
y > -3; y ≥ 2/3x - 4
y < -3; y ≥ 2/3x - 4
y > -2; y ≤ 2/3x - 4
Answers
The system that has linear inequalities has the point (3, -2) in its solution set is y > -3; y ≥ 2/3x - 4.
We know that
If a ordered pair is a solution of the system of inequalities, then the ordered pair must satisfy both inequalities (makes true both inequalities)
In option B, we have
y > -3 ----> inequality A
y ≥ 2/3x - 4 ----> inequality B
In both inequality, change the values of x and y at the point (3, -2) and then compare the outcomes.
Inequality A
y > -3 ----> is true
Inequality B
y ≥ 2/3x - 4 ----> is true
Therefore
The ordered pair is a solution of the system B
As a result, the point (3, -2) in the solution set of the system with linear inequalities is y > -3; y 2/3x - 4.
To learn more about linear inequalities click here:
brainly.com/question/11897796
#SPJ4
Each question on a multiple choice exam has four choices. One of the choices is the correct answer, worth five points another choice is wrong but still carries partial credit of 1 point and other two choices are worth 0 points. If the student picks answers at random, what is the expected value of his or her score for a problem?
Answers
If a student picks randomly then the expected value of his or her score for a problem is 1.5.
Each question on a multiple-choice exam has four choices.
One of the choices is correct, worth four points.
Another choice is wrong but carries partial credit for one point.
The other two choices are wrong and worth a negative one point.
Each has a probability of getting selected is 0.25.
\(0.25*5+0.25*1+0.25*0+0.25*0\)
\(1.25+0.25\)
\(1.5\)
What is the expected value?
The expected value denotes potential. The occurrence of a random event is the subject. Its fundamental notion is that something is probable to occur.
Actually, the anticipated value may be viewed as the mean of a random variable. This indicates that the anticipated value is the average of all the values acquired if a probability experiment were repeated again while keeping track of the outcomes. The anticipated value of a game of chance is what you should expect to occur over the long run of several trials.
Learn more about expected valuehttps://brainly.com/question/14723169
#SPJ1
which diagram below appears to show a pair of perpendicular lines Diagram A Diagram B Diagram C. Explain your Answer.
Answers
The answer for it is diagram B because it does not cross or have parallel lines
7. Ricardo paid $15 for 4 pounds of almonds. At this price, how much would he pay for 10 pounds of
almonds? You must write as a proportion before solving.
Answers
Answer:
$37.50
Step-by-step explanation:
First, create a proportion:
\(\frac{15}{4}\) = \(\frac{x}{10}\)
Then, cross multiply and solve for x:
150 = 4x
37.5 = x
So, 10 pounds of almonds will cost $37.50
The dimensions of a miniature model are proportional to the dimensional of the actual building
Answers
Answer:
The model and the actual building would be similar
Step-by-step explanation:
The quantity r varies jointly with t and u and inversely with s when t= -12, u= -7, and s= -4, r= -126. Find r when t= -8, u= 8, and s= -6.
Write your answer in exact form.
Answers
Answer:
r = 64
Step-by-step explanation:
r = (k*t*u)/s
Where,
k = constant of proportionality
t = -12,
u= -7,
s= -4,
r= -126.
r = (k*t*u)/s
-126 = (k*-12*-7)/-4
-126 * -4 = 84k
504 = 84k
k = 504/84
k = 6
Find r when t= -8, u= 8, and s= -6.
r = (k*t*u)/s
= (6*-8*8) / -6
= -384 / -6
= 64
r = 64
