ANSWER BRIEFLY AND FAST FOR GUARANTEED BRAINLY AND POINTS!
• commutative property
• addition property of equality
• 2x=8
• distributive property
• division property of equality
• x=4
• multiplication property of equality
• subtraction property of equality

Answers
Answer:
See below
Step-by-step explanation:
\(2(x+5)-3 =15\)
Using the distributive property in the LHS we get
\(2x+10-3 =15\)
\(2x+7=15\)
Now add -7 both sides. So we have the subtraction property of equality.
\(2x+7+(-7)=15+(-7) \text{ This is what I meant for add}\)
\(2x+7-7=15-7\)
\(2x=8\)
Now divide both sides by 2. So we have the division property of equality
\(\dfrac{2x}{2} =\dfrac{8}{2}\)
\(x=4\)
Related Questions
Mario received $0.40 in change from
$20.00 when he bought trail mix. How
many pounds of trail mix did Mario buy?
Answers
$19.60 ÷ ($3.50/1 lb) = 5.6 lbs
Mario bought 5.6 pounds of trail mix
Find the surface area of a triangular prism of length 25cm height 4.5 and base 6cm
Answers
The surface area of the triangular prism is 447.5 cm²
Given,
The length of the triangular prism, L = 25 cm
The height of the triangular prism, h = 4.5 cm
The base of the triangular prism, b = 6 cm
We have to find the surface area of the triangular prism.
Surface area of a triangular prism = (Perimeter of base × length of the prism) + (2 × base area)
We have to find the sides of the base of the triangular prism:
For that we can use Pythagorean theorem:
Hypotenuse² = altitude² + base²
Here, altitude = 4.5 and base = 6/2 = 3
Now,
Hypotenuse² = 4.5² + 3² = 20.25 + 9 = 29.25
Hypotenuse = \(\sqrt{29.25}\) = 5.41 cm
Now perimeter of the base of the triangular prism
= (5.41 × 2) + 6 = 10.82 + 6 = 16.82 cm
Next base area:
Base area = 1/2 bh = 1/2 × 6 × 4.5 = 3 × 4.5 = 13.5 cm²
So,
Surface area = (16.82 × 25) + (2 × 13.5) = 420.5 + 27 = 447.5 cm²
That is, the surface area of the triangular prism is 447.5 cm²
Learn more about triangular prism here:
https://brainly.com/question/16551265
#SPJ1
please help
if x = 3 and y=-4 find x2 + y2 and x2 -y2
Answers
(3)2 + y2 = for x2 + y2
(3)2 - y2 = for x2 - y2
This would get you for both equations..
6 + y2 = for x2 + y2
6 - y2 = for x2 - y2
2. Now let’s plug in the value of y which is -4:
6 + (-4)2 = for x2 + y2
6 - (-4)2 = for x2 + y2
This would get you for both equations...
-2 = x2 + y2
14 = x2 - y2
Hope this helped, have an awesome day!
Keisha and Angelica bought a basket of apples. Keisha bought 5 4 pounds. If together, they bought 19 4 pounds of apples, how many pounds of apples did Angelica buy? Let A = the number of pounds of apples Angelica bought.
Answers
Answer:
1. C 2.B .
Step-by-step explanation:
answer : 1. A+ 5/4 +19/4 ,,,,, 2. 14/4 = 7/2
Hope it helps :)
Answer:
What is the equation that models this scenario?
✔ A + 5/4 = 19/4
and
How many pounds of apples did Angelica buy?
✔ 14/4 = 7/2
Step-by-step explanation:
Hope this helps!! :)
1)
f(x) = 2|x-4| + 3
a =
h =
K=
Vertex = ( , )
Answers
Answer:
See below
Step-by-step explanation:
f(x) = a(x - h)^2 + k
f(x) = 2(x-4)^ 2 +3 ? correct me If incorrect
a h k
a= 2
h = 4
k = 3
vertex = (h, k)
vertex= (4,3)
How many different 9-letter "words" can you
make by arranging the letters in DEVIATION?
The arrangements don't have to be actual words
that are included in any dictionary.
Answers
There are 5040 different 9-letter “words” that can be made by arranging the letters in DEVIATION.
The given word is DEVIATION and we are required to find out the number of different 9-letter “words” that can be formed by arranging its letters.
To solve the problem, we will use the formula for finding permutations of n objects taken r at a time when all the objects are distinct.
The formula is given by: nPr = n! / (n-r)! where n is the total number of objects and r is the number of objects to be selected.
Here, we have 9 objects (letters) and we need to arrange all of them, so r = 9.
Now, we need to find out the value of n.
The given word DEVIATION has 9 letters, but two of them (E and I) are repeated twice.
Therefore, n = 9 - 2 = 7.
We will substitute these values in the formula to get the required answer:
nPr = n! / (n-r)! = 7! / (7-9)! = 7! / (-2)! = 7! / 1 = 5040
Therefore, there are 5040 different 9-letter “words” that can be made by arranging the letters in DEVIATION.
For more questions on permutations
https://brainly.com/question/28065038
#SPJ8
0.25 1 4 16 64 enter the values used in finding a partial sum. r = a1 = n =
Answers
A geometrical series have a constant ratio. The value of r is 4, while the value of a1 is 0.25 and the value of n is 5.
What is geometrical series?A geometrical series is a series of numbers where the quotient of any two consecutive terms of the series is constant.
The given series is a geometrical series which is given as, 0.25, 1, 4, 16, 64.
Now the value of r is the ratio of any two consecutive terms of the geometrical series therefore, the value of r can be written as,
\(r = \dfrac{1}{0.25}=4\)
The a1 of a geometrical series is the first term of the series, therefore, the value of a1 can be written as,
a1 = 0.25
The n is the number of terms in a geometrical series, therefore, the value of n can be written as
n = 5
Hence, the value of r is 4, while the value of a1 is 0.25 and the value of n is 5.
Learn more about Geometrical Sequence:
https://brainly.com/question/4617980
Answer:
r = 4
a1 = 0.25
n = 5
b for the last 2
Step-by-step explanation:

Assume that z-scores are normally distributed with a mean of O and a standard deviation of 1. If P( - b< z
Answers
The given z-scores are normally distributed with a mean of 0 and standard deviation of 1. We are required to find the value of b. The given probability is P(-b < z < b) = 0.9984. The region we are interested in lies between -b and +b.
In order to find the value of b, we need to find the z-score corresponding to the given probability of 0.9984. We can use a standard normal distribution table to find the value of b.We can see from the table that the area between 0 and 2.97 is 0.9984. Therefore, we can write: P(-2.97 < z < 2.97) = 0.9984The region between -2.97 and 2.97 represents 99.84% of the area under the standard normal distribution curve. In other words, 99.84% of all possible z-scores lie within this range. So, we can write: P(-b < z < b) = 0.9984Using the values we found above, we can set up the following inequality:-2.97 < -b or b < 2.97Solving for b, we get:-b < -2.97 or b < 2.97b > 2.97 or b < -2.97Therefore, the range of values of b is: -2.97 < b < 2.97
The probability that a z-score lies between -b and b is given as P(-b < z < b) = 0.9984. To find the value of b, we need to use a standard normal distribution table. From the table, we can see that the area between 0 and 2.97 is 0.9984. Therefore, P(-2.97 < z < 2.97) = 0.9984. This means that 99.84% of all possible z-scores lie between -2.97 and 2.97. To find the range of values of b, we set up the inequality -2.97 < -b or b < 2.97. Solving for b, we get -b < -2.97 or b < 2.97. Therefore, the range of values of b is -2.97 < b < 2.97.
To know more about deviation visit:
https://brainly.com/question/31835352
#SPJ11
What is the 100th digit of pi?what is the hundredth digit of pi? this would include the 3 in the beginning.
Answers
100th digit of the pi is 7
Pi (represented by the Greek letter π) is a mathematical constant that represents the ratio of the circumference of a circle to its diameter. It is approximately equal to 3.14159,
The decimal representation of pi (π) is an infinite non-repeating sequence of digits, so there is no simple formula or algorithm to determine the value of its digits. However, you can use a computer program or online tool to calculate the digits of pi to a certain number of decimal places.
Assuming you are looking for the 100th decimal digit of pi, it is 7. This means that if you write out the first 100 digits of pi, the 100th digit is 7.
Learn more about Pi here
brainly.com/question/16277677
#SPJ4
given the circle, find the arc measure

Answers
Find and evaluate the integral taking Ω:0≤x^2+y^2≤1 for ∫∫(x+3y^3)dxdy?
Answers
The integral to evaluate is ∫∫(x+3y³)dxdy over the region Ω: 0≤x²+y²≤1 is evaluated to π.
First, let's convert to polar coordinates: x = r*cos(θ) and y = r*sin(θ). Then, the region Ω becomes 0≤r≤1, 0≤θ≤2π. The integral in polar coordinates is:
∫(θ=0 to 2π) ∫(r=0 to 1) (r*cos(θ) + 3r³*sin(θ)³) * r dr dθ
Now, separate the integrals for easier evaluation:
∫(θ=0 to 2π) (cos(θ)dθ) * ∫(r=0 to 1) (r² dr) + ∫(θ=0 to 2π) (3sin(θ)³ dθ) * ∫(r=0 to 1) (r⁴ dr)
Evaluating these integrals separately and summing the results, we find that the integral evaluates to π.
To know more about integral click on below link:
https://brainly.com/question/31109342#
#SPJ11
use the venn diagram to compare and contrast the definitions of the linnaean class answers
Answers
The Linnaean class system provides a framework for understanding the diversity of life on Earth by grouping similar organisms together based on shared characteristics.
By comparing and contrasting the definitions of each class, we can see how different groups of animals are related to each other and how they differ in terms of their biological traits.
The Linnaean class system is a way of organizing living things based on shared characteristics. Let's compare and contrast the definitions of the Linnaean classes using a Venn diagram.
First, we have the class Mammalia, which includes all animals that have hair or fur, produce milk to feed their young, and have specialized teeth. This class overlaps with the class Aves, which includes all birds, because some birds have specialized beaks and feathers that are similar to mammalian hair and teeth. However, birds do not produce milk.
Next, we have the class Reptilia, which includes animals that are cold-blooded, lay eggs, and have scales or plates on their skin. This class overlaps with both Mammalia and Aves in terms of species that lay eggs, such as monotremes (platypus and echidnas) and some birds (ostriches and emus). However, reptiles lack specialized teeth and do not produce milk.
Finally, we have the class Amphibia, which includes animals that are cold-blooded, breathe through their skin, and undergo metamorphosis from a water-dwelling larval stage to a land-dwelling adult stage. This class overlaps with Reptilia in terms of some shared characteristics, but Amphibia also lacks specialized teeth and does not lay eggs with hard shells like reptiles.
More on Linnaean class system: https://brainly.com/question/2548027
#SPJ11
A poll conducted by the UC Berkeley Institute of Governmental studies in 2019 found that 51.7% of 4527 respondents said they considered moving out of the state.Here n=4527 and p^=51.7=0.517 , andq^=1-p^=1-0.517=0.483Now to compute 95% confidence interval for the proportion of all California who considered moving out of state.
Answers
The 95% confidence interval for the proportion of all Californians who considered moving out of state is (0.504, 0.530). We can be 95% confident that the true proportion of all Californians who considered moving out of state lies between 50.4% and 53.0%.
The UC Berkeley Institute of Governmental Studies conducted a poll in 2019 with 4,527 respondents in California, where 51.7% of them reported considering moving out of the state. The objective is to calculate a 95% confidence interval for the proportion of all Californians who considered moving out of state, given the sample size and proportion.
B. The formula to calculate the confidence interval for a proportion is:
CI = p^ ± z* √[(p^(1-p^))/n]
Where p^ is the sample proportion, n is the sample size, and z* is the critical value of the standard normal distribution for the desired confidence level. For a 95% confidence level, z* = 1.96.
Substituting the given values into the formula, we get:
CI = 0.517 ± 1.96 * √[(0.517*(1-0.517))/4527]
CI = 0.517 ± 0.013
The 95% confidence interval for the proportion of all Californians who considered moving out of state is (0.504, 0.530). Therefore, we can be 95% confident that the true proportion of all Californians who considered moving out of state lies between 50.4% and 53.0%.
For more questions like Sample click the link below:
https://brainly.com/question/31101410
#SPJ11
Ms. Raab and Ms. Levy both drink coffee in the
mornings.
Ms. Raab adds 1 more teaspoon to each cup of
coffee than Ms. Levy. Together, they both add 5
teaspoons of sugar to their coffees.
How many teaspoons of sugar does Ms. Raab add?
How many teaspoons does Ms. Levy add?
Set up an equation to show this, and then solve.
Answers
Answer:
Ms Levy = 2
Ms Rabb = 3
Step-by-step explanation:
Let :
Number of teaspoons taken by Ms Levy = x
Number of teaspoons taken by Ms Rabb = x + 1
Total number of teaspoons taken by both = 5
(Number of teaspoons taken by Ms Rabb + Number of teaspoons taken by Ms Levy) = total number of teaspoons taken
x + 1 + x = 5
2x + 1 = 5
2x = 5 - 1
2x = 4
x = 4/2
x = 2
Hence,
Number of teaspoons of sugar added by Ms Levy = x = 2
Number of teaspoons of sugar added by Ms Rabb = x + 1 = 2 + 1 = 3
What is the solution of Chinese Remainder Theorem?
Answers
The solution of the Chinese Remainder Theorem can be calculated by using the formula: \({\displaystyle x=\sum _{i=1}^{k}a_{i}M_{i}N_{i}.}\)
According to the Chinese remainder theorem, if one knows the remainders of the Euclidean division of an integer n by multiple numbers, one may uniquely calculate the remainder of the division of n by the product of these integers, provided that the divisors are pairwise coprime (no two divisors share a common factor other than 1).
For example, if we know that the remainder of n divided by 3 is 2, the remainder of n divided by 5 is 3, and the remainder of n divided by 7 is 2, we may calculate the remainder of n divided by 105 (the product of 3, 5, and 7) without knowing the value of n. This tells us that if n is a natural number less than 105, then the only possible value of n is 23.
Learn more about Chinese Remainder Theorem;
https://brainly.com/question/13202290
#SPJ4
A model house is 2 cm tall. If it was built
with a scale of 1 cm : 7 m, then how tall is
the real house?
Answers
Answer:
14m=1400cm
Step-by-step explanation:
100cm=1m
7m=700cm
And the model is 2 cm
So the real length is 1400cm or 14m
Enter the degree of the polynomial
below. 6x6 +9x³+3x² - 4x¹0 - 9x5 – 5x6 A. 4 B. 9 C. 6 D. 10
Answers
Answer:
10
Step-by-step explanation:
Degree is the highest exponent
PLEASE HELP ASAP!!!!!

Answers
Answer:
Factored completely is: 3x^2 (x+3)(x-2)
according to your question - probs (x-2), no other choice
Step-by-step explanation:
have fun friend & have a good day friend :)
Let Z be the variable for the Standard normal distribution. Given that P(0 < Z < a) = 0.4793. Find a.
a. -0.52
b. 2.04
c. -2.04
d. 0.84
Answers
We are given that P(0 < Z < a) = 0.4793, where Z is a standard normal random variable. We need to find the value of a that satisfies this probability.
In the standard normal distribution, the area under the curve between 0 and a represents the probability of observing a value between 0 and a. We are given that this probability is 0.4793.
To find the value of a, we can use the standard normal distribution table or a calculator that provides the cumulative distribution function (CDF) for the standard normal distribution. We look for the corresponding probability value of 0.4793 in the table or use the CDF function to find the corresponding z-score.
Looking up the value of 0.4793 in the standard normal distribution table or using a calculator, we find that the z-score corresponding to this probability is approximately -0.06. Therefore, a value of a that satisfies P(0 < Z < a) = 0.4793 is approximately -0.06.
None of the given answer choices (-0.52, 2.04, -2.04) match the calculated value. Thus, none of the options are the correct value for a in this case.
To learn more about variable click here:
brainly.com/question/15078630
#SPJ11
can anyone answer this?

Answers
Answer:
C
Step-by-step explanation:
Answer:
(3,4), (4,-3)
Step-by-step explanation:
When finding a point on a graph, do the x-axis first, then the y-axis. For this equation, move three to the right on the x-axis, then move upward 4 times to get to the point. Or move up 4 times, then 3 to the right. Hope this helps!
Determine whether the given set of functions is linearly independent on the interval (-infinity, infinity). f_1(x) - x, f_2(x) = x^2, f_3(x) = 3x - 6X^2 linearly dependent linearly independent
Answers
The given set of functions {f_1(x) = x, f_2(x) = x^2, f_3(x) = 3x - 6x^2} is linearly independent on the interval (-infinity, infinity).
Linear independence of a set of functions means that no function in the set can be expressed as a linear combination of the other functions. In other words, for the set to be linearly independent, the only solution to the equation c_1f_1(x) + c_2f_2(x) + c_3f_3(x) = 0 should be c_1 = c_2 = c_3 = 0, where c_1, c_2, and c_3 are constants.
To determine if the given set is linearly independent, we need to check if there exist non-zero constants c_1, c_2, and c_3 such that c_1f_1(x) + c_2f_2(x) + c_3f_3(x) = 0 for all x in the interval (-infinity, infinity).
By substituting the functions into the equation and equating the coefficients of the terms with the same powers of x, we can solve for c_1, c_2, and c_3. If the only solution is c_1 = c_2 = c_3 = 0, then the set is linearly independent. In this case, the given set is indeed linearly independent as there is no non-zero solution to the equation, confirming that the functions are not dependent on each other.
To know more about infinity click here: brainly.com/question/22443880
#SPJ11
Under her cell phone plan, Ava pays a flat cost of $58 per month and $4 per gigabyte.
She wants to keep her bill at $62.40 per month. How many gigabytes of data can she
use while staying within her budget?
Answers
62.4=4x+58
Step 1) add like variables by subtracting 58 from both sides
62.4-58=4x+58-58
4.4=4x
Step 2) divide both sides by 4 to get x
x= 1.1
Answer is 1.1 gigabytes
College Algebra Applied Problem Four A medical professional is helping an individual balance their diet. The individual has asked for some certain foods to remain in their diet. They will always get 600 calories from carbohydrates. The individual says that they can be flexible about how many calories they consume in fats and proteins. The goal of the diet is to keep the individual at 1,800 calories per day ( 600 of which come from carbohydrates). Part One Write an equation that models the amount of calories from fats " f ' and protein "p" that the individual can consume in order to reach 1,800 calories. Part Two The diet being prescribed to the individual calls for calories from protein to be three times the calories from fat. Write an equation based on this information that relates calories from protein "p" to calories from fat " f ". Part Three Use your equations from parts "b" and "c" to solve this system of equations and determine the amount of calories that the individual should consume from fats and proteins. Part Four If the individual no longer required 600 calories from carbohydrates, and instead said that they would be flexible about how many carbohydrates they would consume, how many variables would there be for this problem on calories?
Answers
The system equation that models the amount of calories from fats (f) and proteins (p) that the individual can consume to reach 1,800 calories is: f + p = 1,200. The equation that relates calories from protein (p) to calories from fat (f) based on the prescribed diet is: p = 3f. Solving the system of equations, we find that the individual should consume 300 calories from fats and 900 calories from proteins.
To find the equation that models the amount of calories from fats and proteins that the individual can consume in order to reach 1,800 calories, we consider that 600 calories will come from carbohydrates. Since the total goal is 1,800 calories, the remaining calories from fats and proteins should add up to 1,800 - 600 = 1,200 calories. Therefore, the equation is f + p = 1,200.
Based on the prescribed diet, the individual is required to consume calories from protein that are three times the calories from fat. This relationship can be expressed as p = 3f, where p represents the calories from protein and f represents the calories from fat.
To solve the system of equations, we substitute the value of p from the second equation into the first equation: f + 3f = 1,200. Combining like terms, we get 4f = 1,200, and dividing both sides by 4 yields f = 300. Substituting this value back into the second equation, we find p = 3(300) = 900.
Therefore, the individual should consume 300 calories from fats and 900 calories from proteins to meet the diet requirements and achieve a total of 1,800 calories.
Learn more about system equation
brainly.com/question/32645146
#SPJ11
Choose the length of the legs of square ABCD.

Answers
The length of the legs of square ABCD is 2√2.
We have,
Applying the Pythagorean theorem.
Square has all sides equal.
So,
4² = x² + x²
16 = 2x²
x² = 8
x = √8
x = √(4 x 2)
x = 2√2
Thus,
The length of the legs of square ABCD is 2√2.
Learn more about the Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ1
**FIRST CORRECT ANSWER GETS 20 POINTS AND BRAINLIEST***

Answers
Answer:
y=2x+2
Step-by-step explanation:
fzucivhxvpjcjcgkgcckvckgjvl xkc
Answer:
A
Step-by-step explanation:
Walter is planning a hiking trip and he estimated the gradient of trail to be 213.6 ft/mile. After hiking and tracking the trail, he found that the trail was actually 202.7 ft/mile. What was his percent error? Did he overestimate or underestimate the gradient?
Answers
Answer: His percent error = 5.38 %
He overestimated the gradient.
Step-by-step explanation:
Formula : \(Percent\ error =\dfrac{|Estimated\ value- Actual\ value|}{Actual\ value}\times100\)
Given, Estimated gradient of trail = 213.6 ft/mile
Actual gradient of trail = 202.7 ft/mile
Since, 213.6 > 202.7 , that means he overestimated the gradient.
Percent error: \(\dfrac{|213.6-202.7|}{202.7}\times100\)
\(=\dfrac{10.9}{202.7}\times100\\\\\approx5.38\%\)
Hence, percent error = 5.38 %
PLZ HELP !!!! Only do B) and C)

Answers
First frame is for b and second frame is for c


Which of the following comparisons is correct?
-2 2
4<−4
−6< −5

Answers
================================================
Explanation:
Let's go through the answer choices
A) This is false because -2 is actually larger than -5. Make a number line and you'll see that -2 is to the right of -5. Numbers on the right are larger than numbers on the left. B) This is also false. The value 0 is smaller than 2. A number line might help show this.C) Also false. It should be 4 > -4. Any positive number is always larger than any negative number. D) This is true. On a number line, -6 is to the left of -5, so -6 is smaller than -5. This makes -6 < -5 a true statement.write the ascending order of 21/50 , 3/50 , 17/25 and 1 , 1/5
Answers
Answer:
1, 1/5, 3/50, 17/25, 21/50 I think
10. Triangle JKL is shown. Based on the information in the diagram, what is the measure of ZJKL? (G6D)
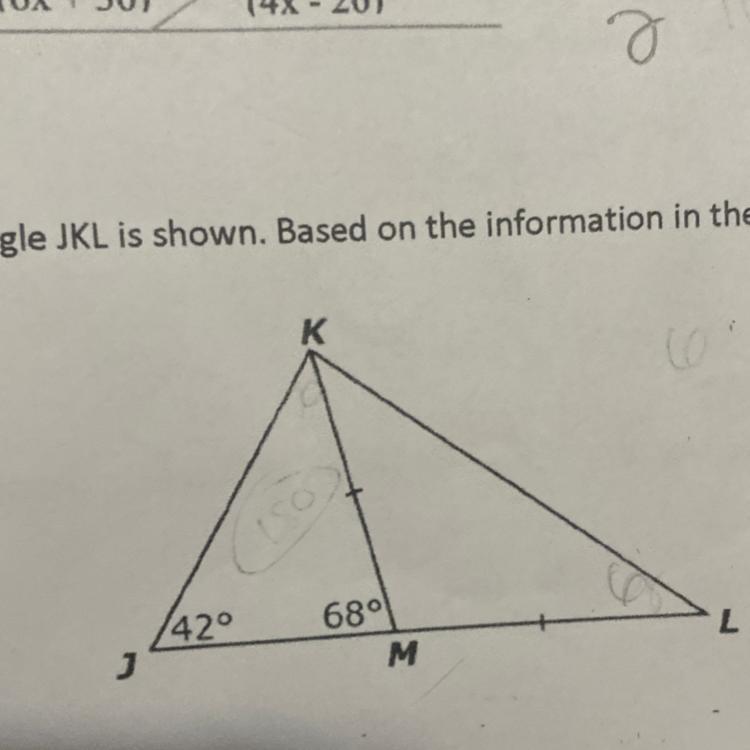
Answers
Answer:
I think this diagram its 110° cause it's measure for ZJKL FOR (G6D)
I