Angle θ is in standard position and
(
−
5
,
−
6
)
(−5,−6) is a point on the terminal side of θ. If
0
∘
≤
θ
<
36
0
∘
0
∘
≤θ<360
∘
, what is the measure of θ, to the nearest tenth of a degree (if necessary)?
Answers
The measure of angle θ, to the nearest tenth of a degree is 233.1°.
To find the measure of angle θ, we need to use trigonometry. We can see that the point (-5,-6) lies in the third quadrant since both x and y coordinates are negative. We can draw a right-angled triangle with the origin (0,0) as the vertex and the given point (-5,-6) as one of the vertices on the x-y plane.
The hypotenuse of this triangle will be the distance between the origin and the point (-5,-6), which can be calculated using the Pythagorean theorem.
Using the Pythagorean theorem, we get:
√(5²+6²) = √(25+36) = √61
Now we can use trigonometry to find the measure of angle θ. We can see that the sine of θ is equal to the opposite side over the hypotenuse and the cosine of θ is equal to the adjacent side over the hypotenuse. So we have:
sin θ = -6/√61 and cos θ = -5/√61
Using a calculator, we can find that θ is approximately 233.1° to the nearest tenth of a degree.
To know more about standard position, refer here:
https://brainly.com/question/30382689#
#SPJ11
Related Questions
help please, i don’t know how to solve #12. this is high school math

Answers
The answers of the following questions are provided below with full solution respectively.
What is coordinate geometry?Coordinate geometry is a branch of mathematics that combines algebra and geometry.
It involves using algebraic equations to describe the positions and relationships between points in a geometric plane.
It is also known as analytic geometry.
a) To find the midpoint of AB, we can use the midpoint formula:
Midpoint = ( (x1+x2)/2, (y1+y2)/2 )
So, the midpoint of AB is:
Midpoint = ( (1+6)/2, (4+(-8))/2 )
= ( 3.5, -2 )
Therefore, the midpoint of AB is (3.5, -2).
b) To find the slope of AB, we can use the slope formula:
Slope = (y2-y1)/(x2-x1)
So, the slope of AB is:
Slope = (-8-4)/(6-1)
= -12/5
Therefore, the slope of AB is -12/5.
c) To find the length of AB, we can use the distance formula:
Distance = √[(x2-x1)² + (y2-y1)²]
So, the length of AB is:
Distance = √[(6-1)² + (-8-4)²]
= √[5² + (-12)²]
= √(169)
= 13
Therefore, the length of AB is 13.
To know more about midpoint formula visit:
https://brainly.com/question/4728902
#SPJ1
Using coordinate geometry, we can find the following:
AB's midpoint is: (3.5, -2)
The slope of AB is -12/5.
The length of AB is 13.
Coordinate geometry is what?Algebra and coordinate geometry are combined in the field of mathematics known as coordinate geometry.
It includes describing the locations and connections between points in a geometric plane using algebraic equations.
Another name for it is analytical geometry.
We can apply the midpoint formula to determine AB's midpoint as follows:
\(Midpoint=\frac{(x_1+x_2)}{2} ,\frac{(y_1+y_2)}{2}\)
Therefore, AB's midpoint is:
Midpoint = ((1+6)/2, (4+(-8))/2)
= (3.5, -2)
Hence, the midpoint of AB is (3.5, -2).
We may use the slope formula to determine the slope of AB:
\(slope=\frac{(y_{2} -y_{1} )}{(x_{2} -x_{1} )}\)
So, the slope of AB is:
Slope = (-8-4)/ (6-1)
= -12/5
Hence, the slope of AB is -12/5.
We may use the distance formula to determine the length of AB:
\(Distance=\sqrt{[(x_{2} -x_{1} )^{2} +(y_{2} -y_{1} )^2]}\)
So, the length of AB is:
Distance = √ [(6-1) ² + (-8-4) ²]
= √ [5² + (-12) ²]
= √ (169)
= 13
Therefore, the length of AB is 13.
To know more about coordinate geometry, visit:
https://brainly.com/question/18269861
#SPJ1
Find the direction of this vector:
-22.2 m
12.6 m
Remember, angles are measured from
the +x-axis.
x-component (m)
Answers
Answer:
Therefore, the direction of the vector is 180° - 29.3° = 150.7° (measured counterclockwise from the positive x-axis).
Step-by-step explanation:
To find the direction of the vector, we need to calculate its angle with respect to the positive x-axis. We can use the inverse tangent function to do this. The formula for the angle θ is:
θ = tan⁻¹ (y/x)
where y is the vertical component and x is the horizontal component of the vector.
In this case, the x-component is -22.2 m and the y-component is 12.6 m. So, we have:
θ = tan⁻¹ (12.6 / (-22.2))
Using a calculator, we find:
θ ≈ -29.3°
Since the x-component is negative, the vector points towards the negative x-axis. Therefore, the direction of the vector is 180° - 29.3° = 150.7° (measured counterclockwise from the positive x-axis).
so nobody is smart enough to answer my question?
Answers
That is ver very sad
yes,
abcdefghijklmnopqrstuvwxyz
An item sells for $75 and is on sale for 35% off. The sales tax is 9.8%. What is the final cost of the item?
Answers
The final cost of the item after a 35% discount and 9.8% sales tax is $53.54.
The given problem is related to percentage discounts and sales tax and can be solved using the following steps:
Step 1: Firstly, we need to determine the discount amount, which is 35% of the original price. Let's calculate it. Discount = 35% of the original price = 0.35 x $75 = $26.25
Step 2: Now, we will calculate the new price after the discount by subtracting the discount amount from the original price.New Price = Original Price - Discount AmountNew Price = $75 - $26.25 = $48.75
Step 3: Next, we need to calculate the amount of sales tax. Sales Tax = 9.8% of New Price Sales Tax = 0.098 x $48.75 = $4.79
Step 4: Finally, we will calculate the final cost of the item by adding the new price and the sales tax.
Final Cost = New Price + Sales Tax Final Cost = $48.75 + $4.79 = $53.54
Therefore, the final cost of the item after a 35% discount and 9.8% sales tax is $53.54.I hope this helps!
For more such questions on final cost
https://brainly.com/question/29509552
#SPJ8
What is the probability that a five-card poker hand has the following? (a) Four Aces (b) Four of a kind (c) Two pairs (not four of a kind or (d) A full house (three of a kind and a pair)(e) A straight (a set of five consecutive a full house) values) (f) No pairs (possibly a straight or flush)
Answers
Answer:
a because it is the one that makes the most sense
Step-by-step explanation:
Answer:
A
Step-by-step explanation:
PLEASE HELP
Which of the following functions has the same horizontal asymptote as the function graphed below

Answers
A function which has the same horizontal asymptote as the function graphed above include the following: A. f(x) = 4^{x + 2} - 3.
What is a horizontal asymptote?In Mathematics, a horizontal asymptote simply refers to a horizontal line (y = b) where the graph of a function approaches the line as the input values (domain or independent value) approach negative infinity (-∞) to positive infinity (∞).
In this context, the line passing through the ordered pair (0, 3) on the graph of this exponential growth function represents a horizontal asymptote and it has an equation of y = 3, as shown in the image attached below.
Read more on horizontal asymptote here: https://brainly.com/question/14492751
#SPJ1

Translate this sentence into an equation.28 is the product of Mai's savings and 2.Use the variable m to represent Mai's savings.N+ローロロメロx 6?

Answers
2m = 28
Explanations:Given the following parameter
Mai's savings = m
The product of Mai's savings and 2 is given as:
\(\text{Product of Mai's savings and 2 = 2m}\)If 28 is equal to the product of Mai's savings and 2, the resulting expression will be given as:
28 = 2m
Hence the required equation is 2m = 28
Write a division for each. a 4×(-16) b.(-7)×12
Answers
Answer:
a. (-2) (2)7
b. (-21) (2)2
How much tax will you pay on an item that costs $35 with a sales tax rate of 6%
Answers
Answer: $37.10.
Step-by-step explanation:
Answer:
37.5
Step-by-step explanation:
you divide by one hundred multiply by the percent and ad the original cost
6x + 3x - x + 9 = 33
Answers
Answer: x=3
Step-by-step explanation:
6x + 3x - x + 9 = 33
Combine like terms:
6x+3x-x=8x
The equation is now 8x+9=33
Subtract 9 on both sides:
8x+9-9=33-9
8x=24
Divide 8 on both sides:
8x/8=24/8
x=3
evaluate the given integral by changing to polar coordinates ∫∫d x^2yda where d is the top half of the disk with center the origin and radius 5
Answers
The value of the integral for the given integral ∬ (\(x^2\)y) dA is:
∫∫ (\(x^2\)y) dA = (625/8) (\(sin^3\)π/3)
= (625/8) (0)
= 0
To evaluate the given integral ∬ (\(x^2\)y) dA, where d represents the top half of the disk with center at the origin and radius 5, we can change to polar coordinates.
In polar coordinates, we have the following transformations:
x = r cosθ
y = r sinθ
dA = r dr dθ
The limits of integration for r and θ can be determined based on the given region. Since we want the top half of the disk, we know that the angle θ will vary from 0 to π, and the radius r will vary from 0 to the radius of the disk, which is 5.
Now, let's evaluate the integral:
∬ (\(x^2\)y) dA = ∫∫ (\(r^2 cos^2\)θ) (r sinθ) r dr dθ
We can simplify the integrand:
∫∫ (\(r^3 cos^2\)θ sinθ) dr dθ
Now, we can integrate with respect to r first:
∫∫ (r^3 cos^2θ sinθ) dr dθ = ∫ [r^4/4 cos^2θ sinθ] |_\(0^5\) dθ
Substituting the limits of integration for r:
∫∫ (\(r^3 cos^2\)θ sinθ) dr dθ = ∫ [625/4 \(cos^2\)θ sinθ] dθ
Now, we can integrate with respect to θ:
∫ [625/4 \(cos^2\)θ sinθ] dθ = (625/4) ∫ [\(cos^2\)θ sinθ] dθ
We can use a trigonometric identity to simplify the integrand further:
\(cos^2\)θ sinθ = (1/2) sin2θ sinθ
= (1/2) \(sin^2\)θ cosθ
∫ [625/4 \(cos^2\)θ sinθ] dθ = (625/4) ∫ [(1/2) \(sin^2\)θ cosθ] dθ
Using a substitution u = sinθ:
du = cosθ dθ
The integral becomes:
(625/4) ∫ [(1/2) \(u^2\)] du = (625/4) (1/2) ∫ \(u^2\) du
= (625/8) (\(u^3\)/3) + C
Substituting back u = sinθ:
(625/8) (\(sin^3\)θ/3) + C
Finally, we need to evaluate the integral over the limits of θ from 0 to π:
∫ [625/4 \(cos^2\)θ sinθ] dθ = [(625/8) (\(sin^3\)π/3) - (625/8) (\(sin^3\) 0/3)]
Since sin(π) = 0 and sin(0) = 0, the second term becomes 0. Therefore, the value of the integral is:
∫∫ (\(x^2\)y) dA = (625/8) (\(sin^3\)π/3)
= (625/8) (0)
= 0
Learn more about Polar Coordinates at
brainly.com/question/31904915
#SPJ4
SECTION A (20 MARKS) QUESTION 1 (a)Identify the relevant population for the below foci, and suggest the appropriate sampling design to investigate the issues, explaining why they are appropriate. Wherever necessary identify the sampling frame as well. 10 marks A public relations research department wants to investigate the initial reactions of heavy soft- drink users to a new all-natural soft drink'. (b) What type of sampling design is cluster sampling? What are the advantages and disadvantages of cluster sampling? Describe a situation where you would consider the use of cluster sampling. 10 marks
Answers
a) The relevant population is the heavy soft-drink users in the given case, and the appropriate sampling design that should be used is stratified random sampling. The list of all heavy soft-drink users is the sampling frame.
b) Cluster sampling refers to a sampling design where population is divided into naturally occurring groups and a random sample of clusters is chosen.
The advantages are efficient, easy to perform, and used when the population is widely dispersed. The disadvantages are sampling errors, have lower level of precision, and have the standard error of the estimate.
a) The relevant population for the public relations research department to investigate the initial reactions of heavy soft-drink users to a new all-natural soft drink is heavy soft-drink users. The appropriate sampling design that can be used to investigate the issues is stratified random sampling.
Stratified random sampling is a technique of sampling in which the entire population is divided into subgroups (or strata) based on a particular characteristic that the population shares. Then, simple random sampling is done from each stratum. Stratified random sampling is appropriate because it ensures that every member of the population has an equal chance of being selected.
Moreover, it ensures that every subgroup of the population is adequately represented, and reliable estimates can be made concerning the entire population. The list of all heavy soft-drink users can be the sampling frame.
b) Cluster sampling is a type of sampling design in which the population is divided into naturally occurring groups or clusters, and a random sample of clusters is chosen. The elements within each chosen cluster are then sampled.
The advantages of cluster sampling are:
Cluster sampling is an efficient method of sampling large populations. It is much cheaper than other types of sampling methods.Cluster sampling is relatively easy to perform compared to other methods of sampling, such as simple random sampling.Cluster sampling can be used when the population is widely dispersed, and it would be difficult to cover the entire population.The disadvantages of cluster sampling are:
Cluster sampling introduces sampling errors that could lead to biased results.Cluster sampling has a lower level of precision and accuracy compared to other types of sampling methods.Cluster sampling increases the standard error of the estimate, making it difficult to achieve the desired level of statistical significance.A situation where cluster sampling would be appropriate is in investigating the effects of a new medication on various groups of people. In this case, the population can be divided into different clinics, and a random sample of clinics can be selected. Then, all patients who meet the inclusion criteria from the selected clinics can be recruited for the study. This way, the study will be less expensive, and it will ensure that the sample is representative of the entire population.
Learn more about Stratified random sampling:
https://brainly.com/question/20544692
#SPJ11
solve sinx = 2x-3 using false position method
Answers
The root of the equation sinx = 2x-3 is 0.8401 (approx).
Given equation is sinx = 2x-3
We need to solve this equation using false position method.
False position method is also known as the regula falsi method.
It is an iterative method used to solve nonlinear equations.
The method is based on the intermediate value theorem.
False position method is a modified version of the bisection method.
The following steps are followed to solve the given equation using the false position method:
1. We will take the end points of the interval a and b in such a way that f(a) and f(b) have opposite signs.
Here, f(x) = sinx - 2x + 3.
2. Calculate the value of c using the following formula: c = [(a*f(b)) - (b*f(a))] / (f(b) - f(a))
3. Evaluate the function at point c and find the sign of f(c).
4. If f(c) is positive, then the root lies between a and c. So, we replace b with c. If f(c) is negative, then the root lies between c and b. So, we replace a with c.
5. Repeat the steps 2 to 4 until we obtain the required accuracy.
Let's solve the given equation using the false position method.
We will take a = 0 and b = 1 because f(0) = 3 and f(1) = -0.1585 have opposite signs.
So, the root lies between 0 and 1.
The calculation is shown in the attached image below.
Therefore, the root of the equation sinx = 2x-3 is 0.8401 (approx).
Learn more about equation
brainly.com/question/29657983
#SPJ11
Verify that the function are solutions to the associated homogeneous differential equation, then find the solution to the ifferential equation:
4x^2y" + y = x^(3/2)sin(x), y(x)= x^(1/2)
Answers
The general solution of the differential equation is y(x) = C₁x¹/² + 1/4 cos(x).
Given a differential equation:
4x²y" + y = x³/² sin(x)
and y(x) = x¹/²
We need to verify whether the given function is the solution of the differential equation or not.
Therefore, we will substitute the value of y(x) in the differential equation.
Let's start by finding the first and second derivatives of y(x) which will be used further.
y(x) = x¹/²y'(x)
= d/dx (x¹/²)y'(x)
= (1/2)x^(-1/2)y''(x)
= d/dx[(1/2)x^(-1/2)]y''(x)
= (-1/4)x^(-3/2)
Therefore, substituting y(x) and y" (x) in the differential equation:
4x² (-1/4)x^(-3/2) + x¹/² = x³/²sin(x)
Thus, the above equation simplifies as:-
x^(-1) + x¹/² = x³/²sin(x)
Here, we can see that the given function is not a solution of the differential equation.
However, we can find the particular solution of the differential equation by the method of variation of parameters.
Where we write the given equation in the standard form:
y'' + [1/4x⁴]y = [x¹/² sin(x)]/4x⁻²
On comparing with the standard form:
y'' + p(x) y' + q(x) y = g(x) where p(x) = 0, q(x) = 1/4x⁴ and g(x) = [x¹/² sin(x)]/4x⁻²
Now, let's calculate the Wronskian for the differential equation as:
W(y₁, y₂) = | y₁ y₂ |-1/4x² 1/4x²-1/2W(y₁, y₂)
= 1/4x³
The particular solution y₂(x) will be:
y₂(x) = -y₁(x) ∫[g(x) y₁(x)] / W(x) dx
Substituting the given value in the above equation, we get:
y₂(x) = -x¹/² ∫[x¹/² sin(x)] / (x³/² 4x⁻²) dx
y₂(x) = -1/4 ∫sin(x) dx
y₂(x) = -1/4 [-cos(x)] + C₁
y₂(x) = 1/4 cos(x) + C₁
Hence, the general solution of the differential equation is:
y(x) = C₁x¹/² + 1/4 cos(x)
To know more about differential visit:
https://brainly.com/question/31433890
#SPJ11
Question 24 Multiple Choice Worth 1 points)
(8.01 MC)
Two lines, A and B, are represented by equations given below:
Line A: y = x - 4
Line B: y = 3x + 4
Which of the following shows the solution to the system of equations and explains why?
0 (-3,-5), because the point satisfies one of the equations
0 (-3,-5), because the point lies between the two axes
(-4,-8), because the point satisfies both equations
(-4, -8), because the point does not lie on any axis
Answers
Given:
The system of equations is:
Line A: \(y=x-4\)
Line B: \(y=3x+4\)
To find:
The solution of given system of equations.
Solution:
We have,
\(y=x-4\) ...(i)
\(y=3x+4\) ...(ii)
Equating (i) and (ii), we get
\(x-4=3x+4\)
\(-4-4=3x-x\)
\(-8=2x\)
Divide both sides by 2.
\(-4=x\)
Substituting \(x=-4\) in (i), we get
\(y=-4-4\)
\(y=-8\)
The solution of system of equations is (-4,-8).
Now verify the solution by substituting \(x=-4, y=-8\) in the given equations.
\(-8=-4-4\)
\(-8=-8\)
This statement is true.
Similarly,
\(-8=3(-4)+4\)
\(-8=-12+4\)
\(-8=-8\)
This statement is also true.
Therefore, (-4,-8) is a solution of the given system of equations, because the point satisfies both equations. Hence, the correct option is C.
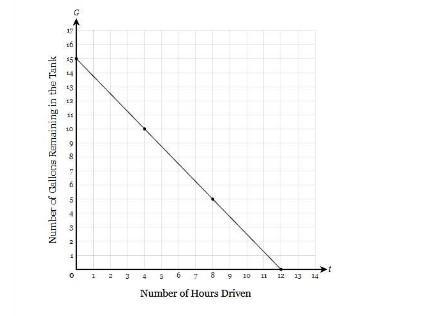
Serenity filled up her car with gas before embarking on a road trip across the country. Let � G represent the number of gallons of gas remaining in her gas tank after driving for � t hours. A graph of � G is shown below. Write an equation for � G then state the � y-intercept of the graph and determine its interpretation in the context of the problem.
Answers
The equation is: G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
How to find the linear equation of the graph?The formula for the equation of a line in slope intercept form is:
y = mx + c
where:
m is slope
c is y-intercept
From the graph, we see that:
y-intercept = 15 gallons
Now, the slope is gotten from the formula:
Slope = (y₂ - y₁)/(x₂ - x₁)
Slope = (10 - 5)/(4 - 8)
Slope = -⁵/₄
Thus, equation is:
G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
Read more about Linear equation graph at: https://brainly.com/question/28732353
#SPJ1
Write the equation of the line that passes through points (-4,-1) & (5,3)
Answers
Step-by-step explanation:
ax+by+c=0 is the equation of a line
using y-y1=m(x-x1)
m=3+1/5+4=4/9
y+1=4/9(x+4) multiplying through 9
9y+9=4(x+4)
9y+9=4x+16
9y+9-4x-16=0
9y-7-4x=0
9y-4x-7=0
then you have your answer
which of the following is the correct factorial notation for dr. elder’s new study?
Answers
Factorial notation is used to represent the product of a series of descending positive integers, and is denoted by an exclamation mark.
For example, 5! represents 5 x 4 x 3 x 2 x 1, which equals 120. If the study involves counting the number of ways a certain group of items can be arranged, factorial notation may be used to express the total number of possible arrangements. However, without knowing the specifics of Dr. Elder's study, it is impossible to provide the correct factorial notation. Therefore, I would recommend providing more details about the study in order to receive a more accurate answer.
To know more about factorial notation visit:
https://brainly.com/question/31876029
#SPJ11
Favian received a $100 gift card to a clothing store.
Using only the gift card, he was able to purchase n
sweaters that cost $32 each and 1 belt for $20. If there
was no tax on the sweaters and belt, which of the
following must be true?
Answers
Answer:
32n = 100 - 20
n = 2.5
he purchased 2 sweaters
Step-by-step explanation:
32n = 100 - 20
If Favian originally had $100 but spent $20 on a belt, he only had 80 left, meaning that 80 = 32n which means that he was able to but 2 sweaters and got $16 back. Therefore the formula would be 32n = 100 - 20
The formula for the number of sweaters will be 32n = 100 – 20.
What is the linear system?A linear system is one in which the parameter in the equation has a degree of one. It might have one, two, or even more variables.
Favian received a $100 gift card to a clothing store.
Using only the gift card, he was able to purchase n sweaters that cost $32 each and 1 belt for $20.
If there was no tax on the sweaters and belt,
Then the equation will be
32n + 1 x 20 = 100
32n + 20 = 100
32n = 80
n = 2.5 ≈ 2
If Favian originally had $100 but spent $20 on a belt, he only had 80 left, meaning that 80 = 32n, which means that he was able to but 2 sweaters and got $16 back.
Therefore, the formula would be 32n = 100 – 20.
More about the linear system link is given below.
https://brainly.com/question/20379472
#SPJ2
Angle D of △DEF is congruent to ∠G of △GHJ. Angle E is congruent to ∠H. Side DE is congruent to side HJ. Can you prove that the two triangles are congruent? Explain your answer.
No image attached.
Answers
Answer:
No
Step-by-step explanation:
"Looking" at our triangles
If Angle D is congruent to Angle G, and angle E is congruent to Angle H, lets call those the first and second vertices of each triangle. If we're trying to prove the triangles congruent, we're trying to prove Triangle DEF is congruent to Triangle GHJ (in that order, since we're already given that the first and second angles correspond between triangles).
Could these triangle be congruent? Yes! As a quick example, imagine two Equilateral triangles with side lengths 5. They are congruent, and they do have the first angle and second angle corresponding pairs congruent, and one of those sides from triangle 1 does match the length of one of the sides in triangle 2. ...and they are congruent triangles.
The problem with the given scenario is that the side they give for triangle 1 (between vertex 1 and 2) is not the corresponding side of triangle 2 (between vertex 2 and 3). This makes it so that we cannot guarantee that the triangles are congruent.
As can be seen in the attached image, I've made Side DE length 2, and put it on a coordinate plane so it's easy to see. Side HJ is also definitely length 2. Clearly, those triangles are not congruent.
When would triangles be congruent?
Going back to the definition of congruent triangles, three corresponding angles and three corresponding sides must be congruent. That's 6 pairs of parts needed to be proven congruent to prove triangles congruent!
Fortunately, there are a number of theorems that can be proven to lessen the amount of pairs of parts needed to be proven congruent and still guarantee that the resulting triangles must be congruent.
There are exactly 5 cases:
SSSSASASAAASHLIt looks like a bunch of alphabet soup, but notice that all of them require 3 pieces of information (even HL, which is Hypotenuse-Leg... since there's a Hypotenuse, it must be a right triangle, so there are a pair of corresponding congruent right angles that are congruent that they don't talk about)
In order to remember which items work, remember that you MUST know 3 parts, and think about all of the way you could know 3 parts:
Scenario 1: Have all 3 side pairs (SSS)
There is only one way that all three sides can be equal, and yes, that is one of the triangle congruence shortcuts.
Scenario 2: Have 2 side pairs & 1 angle pair
There are two option here.
two sides and the angle between them (SAS), ortwo sides and an angle NOT between them (...nope).Two sides with the angle between them is SAS (note the angle is between them).
Two sides with the angle not between them is ... (well, that can get you in trouble). Conveniently, that is NOT one of the triangle congruence theorems. So, stay out of trouble, and don't use this for triangle congruence.
Interestingly, HL, is a special case of this "trouble case". Note that if you have the Hypotenuse and a leg, that's two Sides. The right Angle is NOT the angle between those two sides (because the hypotenuse is always across from the right angle). When that angle is 90 degrees, then the set of two sides and the angle not between them DOES work as sufficient to prove triangle congruence, and it's the only time that it's sufficient.
Scenario 3: Have 1 Side and 2 Angles
Again, there are two option here:
two Angles and the Side between them (ASA), ortwo Angles and a Side NOT between them (AAS).In either scenario, this is sufficient to prove the triangles are congruent.
Scenario 4: Have all 3 angles (AAA)
This definitely won't be enough to prove congruence. Zoom in. It's got the same angles, but not the same lengths.
So, only 5 short ways to prove triangles are congruent, and all of them require 3 parts of one triangle corresponding to 3 parts of another, each of the 3 pairs must be congruent.

Determine whether WX and YZ are parallel, perpendicular, or neither
W(-6, -6),x(5,8), Y(4,7), Z(-1,0)
a. parallel
b. neither
c. perpendicular
Answers
jill counted 20 pigs and chickens in the farmyard. jack counted a total of 54 legs for the 20 animals. how many pigs and how many chickens were there?
Answers
As average animal has four legs, there were ten pigs and ten chickens, giving a total of 54 legs: 10 x 4 = 40 legs, 10 x 2 = 20 legs.
10 pigs and 10 chickens were present. 10 pigs have 4 legs each, for a total of 40 legs. 10 chickens have 2 legs each, for a total of 20 legs. 40 + 20 = 54 legs. Jill counted the animals in the farmyard and found twenty. The 20 animals had a total of 54 legs, according to Jack. We can perform a straightforward step-by-step computation to determine the number of pigs and chicks present. Since each pig has four legs, we may generate 40 legs by multiplying the number of pigs, 10, by 4. Similar to humans, chickens have two legs each, so multiplying 10 by 2 results in 20 legs. The sum of the two figures gives us 54 legs, which is the same as Jack's estimate. Hence, the farmyard contained 10 pigs and 10 hens.
Learn more about average here
https://brainly.com/question/24057012
#SPJ4
Need help with this!

Answers
The output of the function call doWork(30) is given as follows:
9.
How to obtain the output of the function?The input of the function is given as follows:
n = 30.
Hence we apply the recursion as follows:
doWork(30) -> return 1 + doWork(15).doWork(15) -> return 1 + doWork(7) -> integer part of the division is 7.doWork(7) -> return 7 -> less than 10.Now we apply the inverse procedure, as follows:
doWork(15) -> return 1 + 7 = 8.doWork(30) -> return 1 + 8 = 9.More can be learned about recursive functions at https://brainly.com/question/30645557
#SPJ1
WILL GIVE brainliest

Answers
Answer:
Below
Step-by-step explanation:
y ( 5.98x - 5.81) - 2.19 y =
5.98xy - 5.81y - 2.19 y
5.98xy + ( - 5.81y - 2.19 y)
5.98xy + ( - 8y )
5.98xy - 8y or y ( 5.98x-8)
you watch a roulette wheel spin 7 consecutive times and the ball lands on a red slot each time. what is the probability that the ball will land on a red slot on the next spin?
Answers
The probability that the ball will fall into a red slot during the following spin is 0.14.
To calculate the probability of an occurrence, divide the total number of outcomes by the total number of possible outcomes. The concepts of probability and odds are distinct. Odds are determined by dividing the probability of a situation happening by the probability that it won't happen. Probability is a metric used to determine how likely an event is to occur. When we toss the coin in the air, the probability that it will land with the heads side up is calculated. Here is a practical use of probability that you are probably already familiar with. We always check the weather forecast before a significant outing.
\(\frac{1}{7}=0.142857\)
The probability is 0.14
Learn more about probability here
https://brainly.com/question/24756209
#SPJ4
The probability of the ball landing on a red slot in a single spin of a fair roulette wheel is 1/2, as there are an equal number of red and black slots.
The outcome of each spin is independent, meaning that the outcome of one spin does not affect the outcome of another. Therefore, the probability that the ball will land on a red slot in the next spin is still 1/2, regardless of the results of the previous seven spins.
Find out more about Roulette wheel
brainly.com/question/20374594
#SPJ4
which triangle has angle measures of 40 , 50 , and 90?

Answers
Answer:
Definitely not the 2nd one. I think it is the first one, the 3rd one looks more like a 45, 45, 90
a metal box that is in shape of cuboid has the following dimensions. the length is 9 inches, width is 2 inches and height is 1. 5 inches. find the total cost of silver coating the entire box if the cost of coating is $2.50 per Sq. inches
Answers
Given:
Length of a box is 9 inches, width is 2 inches and height is 1.5 inches.
The cost of silver coating is $2.50 per sq. inches.
To find:
The total cost of silver coating for the box.
Solution:
The total surface area of a cuboid is
\(A=2(lb+bh+hl)\)
Where, l is length, b is breadth and h is height.
Putting \(l=9,b=2,h=1.5\), we get
\(A=2(9\times 2+2\times 1.5+1.5\times 9)\)
\(A=2(18+3+13.5)\)
\(A=2(34.5)\)
\(A=69\)
So, the total surface area of the box is 69 square inches.
Cost of silver coating is $2.50 per sq. inches. So, the cost of silver coating for the box is
\(Cost=69\times 2.50\)
\(Cost=172.50\)
Therefore, the cost of silver coating for the box is $172.50.
some people who bought x-game gaming systems complained about having received defective systems. the industry standard for such gaming systems has been 98% non-defective systems. in a sample of 120 units sold, 6 units were defective. you calculated your test statistic to see if the percentage of defective systems produced by x-game has exceeded the industry standard. based on your hypothesis and test statistics calculated in the previous question, what is your p-value?
Answers
we can reject the null hypothesis at the 5% significance level since the p-value is less than 0.05.
To calculate the p-value, we need to perform a hypothesis test.
Let's assume the null hypothesis is that the proportion of defective systems produced by x-game is equal to or less than the industry standard of 0.02, while the alternative hypothesis is that the proportion is greater than 0.02.
We can use the normal approximation to the binomial distribution since we have a large sample size (n=120) and np and n(1-p) are both greater than or equal to 10.
The test statistic can be calculated as:
\(z = (p_hat - p) / \sqrt{(p*(1-p)/n)}\)
where \(p_hat\) is the sample proportion of defective systems, p is the hypothesized proportion under the null hypothesis, and n is the sample size.
Using the values given in the question, we have:
\(p_hat = 6/120 = 0.05\)
p = 0.02
n = 120
Plugging these values into the formula, we get:
\(z = (0.05 - 0.02) / \sqrt{(0.02*(1-0.02)/120) = 2.041}\)
The p-value can be calculated as the probability of getting a test statistic as extreme or more extreme than 2.041 under the null hypothesis.
Since this is a one-tailed test (the alternative hypothesis is one-sided), we look up the area in the right tail of the standard normal distribution table.
Using a standard normal distribution table, we find that the area to the right of 2.041 is 0.0207.
Therefore, the p-value is 0.0207.
Therefore, we can reject the null hypothesis at the 5% significance level since the p-value is less than 0.05.
This means that there is strong evidence that the proportion of defective systems produced by x-game exceeds the industry standard of 0.02.
For similar question on hypothesis.
https://brainly.com/question/29690266
#SPJ11
Which tiles should be added to the model below to make zero? 6 negative tiles. 6 negative tiles 6 positive tiles 3 negative tiles and 3 positive tiles 6 negative tiles and 6 positive tiles
Answers
Answer:
Step-by-step explanation:
-6+6=0 -3+3=0
This is because the signs are different so you count back starting with the negatives.
-6,-5,-4,-3,-2,-1,0
Answer:
B) 6 positive tiles
Step-by-step explanation:
A soccer player uses her head to hit a ball up in the air from a height of 1 meters with an initial vertical velocity of 5 meters per second. The height h in meters of the ball is given by h = −4.9t2 + 5t + 1, where t is the time elapsed in seconds. How long will it take the ball to hit the ground if no other players touch it? Enter the time to two decimal places.
Answers
Answer:
It will take 1.19 seconds for the ball to hit the ground if no other players touch it
Step-by-step explanation:
The height of the ball after t seconds is given by the following equation:
\(h(t) = -4.9t^{2} + 5t + 1\)
How long will it take the ball to hit the ground if no other players touch it?
This is t when h(t) = 0. So
\(-4.9t^{2} + 5t + 1 = 0\)
Solving a quadratic equation:
Given a second order polynomial expressed by the following equation:
\(ax^{2} + bx + c, a\neq0\).
This polynomial has roots \(x_{1}, x_{2}\) such that \(ax^{2} + bx + c = a(x - x_{1})*(x - x_{2})\), given by the following formulas:
\(x_{1} = \frac{-b + \sqrt{\bigtriangleup}}{2*a}\)
\(x_{2} = \frac{-b - \sqrt{\bigtriangleup}}{2*a}\)
\(\bigtriangleup = b^{2} - 4ac\)
In this question:
\(-4.9t^{2} + 5t + 1 = 0\)
So \(a = -4.9, b = 5, c = 1\)
So
\(\bigtriangleup = 5^{2} - 4*4.9*1 = 44.6\)
\(t_{1} = \frac{-5 + \sqrt{44.6}}{2*(-4.9)} = -0.17\)
\(t_{2} = \frac{-5 - \sqrt{44.6}{2*(-4.9)} = 1.19\)
Since we want a time measure, the answer cannot be negative.
It will take 1.19 seconds for the ball to hit the ground if no other players touch it