Andres Michael bought a new boat. He took out a loan for $24,180 at 4.5% interest for 4 years. He made a $4,650 partial payment at 4 months and another partial payment of $3,400 at 6 months. How much is due at maturity? (Do not round intermediate calculations. Round your answer to the nearest cent.)
Answers
Answer:
$25,381.94
Step-by-step explanation:
45% interest in 2 years = 45/24 = 1.875% monthly
Debt at month 0 (when Andres got the loan)
24,320
Debt at month 1
24,320*(1 + 0.001875) = 24,365.6
Debt at month 2
24,365.6*(1.001875) - 54.110 (partial payment) = 24,357.1755
Debt at month 3
24,357.1755*(1.001875)
Debt at month 4
Debt at month 5
Debt at month 6
- 3,410 (partial payment)
= 24,540.36874
Debt at month 7
24,540.36874*(1.001875)
Debt at month 8
Debt at month 9
and so on until month 24 (the maturity)
Debt at maturity
= 25,381.93916 = $25,381.94 rounded to the nearest hundreth.Answer:
$25,381.94
Step-by-step explanation:
45% interest in 2 years = 45/24 = 1.875% monthly
Debt at month 0 (when Andres got the loan)
24,320
Debt at month 1
24,320*(1 + 0.001875) = 24,365.6
Debt at month 2
24,365.6*(1.001875) - 54.110 (partial payment) = 24,357.1755
Debt at month 3
24,357.1755*(1.001875)
Debt at month 4
Debt at month 5
Debt at month 6
- 3,410 (partial payment)
= 24,540.36874
Debt at month 7
24,540.36874*(1.001875)
Debt at month 8
Debt at month 9
and so on until month 24 (the maturity)
Debt at maturity
= 25,381.93916 = $25,381.94 rounded to the nearest hundreth.Answer:
$25,381.94
Step-by-step explanation:
45% interest in 2 years = 45/24 = 1.875% monthly
Debt at month 0 (when Andres got the loan)
24,320
Debt at month 1
24,320*(1 + 0.001875) = 24,365.6
Debt at month 2
24,365.6*(1.001875) - 54.110 (partial payment) = 24,357.1755
Debt at month 3
24,357.1755*(1.001875)
Debt at month 4
Debt at month 5
Debt at month 6
- 3,410 (partial payment)
= 24,540.36874
Debt at month 7
24,540.36874*(1.001875)
Debt at month 8
Debt at month 9
and so on until month 24 (the maturity)
Debt at maturity
= 25,381.93916 = $25,381.94 rounded to the nearest hundreth.Answer:
$25,381.94
Step-by-step explanation:
45% interest in 2 years = 45/24 = 1.875% monthly
Debt at month 0 (when Andres got the loan)
24,320
Debt at month 1
24,320*(1 + 0.001875) = 24,365.6
Debt at month 2
24,365.6*(1.001875) - 54.110 (partial payment) = 24,357.1755
Debt at month 3
24,357.1755*(1.001875)
Debt at month 4
Debt at month 5
Debt at month 6
- 3,410 (partial payment)
= 24,540.36874
Debt at month 7
24,540.36874*(1.001875)
Debt at month 8
Debt at month 9
and so on until month 24 (the maturity)
Debt at maturity
= 25,381.93916 = $25,381.94 rounded to the nearest hundreth.Answer:
$25,381.94
Step-by-step explanation:
45% interest in 2 years = 45/24 = 1.875% monthly
Debt at month 0 (when Andres got the loan)
24,320
Debt at month 1
24,320*(1 + 0.001875) = 24,365.6
Debt at month 2
24,365.6*(1.001875) - 54.110 (partial payment) = 24,357.1755
Debt at month 3
24,357.1755*(1.001875)
Debt at month 4
Debt at month 5
Debt at month 6
- 3,410 (partial payment)
= 24,540.36874
Debt at month 7
24,540.36874*(1.001875)
Debt at month 8
Debt at month 9
and so on until month 24 (the maturity)
Debt at maturity
= 25,381.93916 = $25,381.94 rounded to the nearest hundreth.Answer:
$25,381.94
Step-by-step explanation:
45% interest in 2 years = 45/24 = 1.875% monthly
Debt at month 0 (when Andres got the loan)
24,320
Debt at month 1
24,320*(1 + 0.001875) = 24,365.6
Debt at month 2
24,365.6*(1.001875) - 54.110 (partial payment) = 24,357.1755
Debt at month 3
24,357.1755*(1.001875)
Debt at month 4
Debt at month 5
Debt at month 6
- 3,410 (partial payment)
= 24,540.36874
Debt at month 7
24,540.36874*(1.001875)
Debt at month 8
Debt at month 9
and so on until month 24 (the maturity)
Debt at maturity
= 25,381.93916 = $25,381.94 rounded to the nearest hundreth.vvvvvv
Related Questions
I need help I will give Brainliest

Answers
Answer:
\( 129° + (x + 19) ° = 180° \: (angles \: on \: a \: straight \: line) \\ x = 180° - (129° + 19°) \\ x = 32°\)
Keisha runs 7 miles in 60 minutes. At the same rate, how many miles would she run in 24 minutes?
Answers
Answer:(24/60)*7=2.8 miles
Step-by-step explanation:
24/60x7
Only #15,17, and 19 please show work THANK YOU

Answers
The magnitude and direction of the vectors are
11. <0,4> :
Magnitude = 4
Direction = 90°
12. <-3,0>:
Magnitude = 3
Direction = 0°
13. <6,5>:
Magnitude = √(61)
Direction = 39.8°
14. <3,7>:
Magnitude = √58
Direction = 66.8°
15. <-2,1>:
Magnitude = √5
Direction = -26.57°
16. <-10,13>:
Magnitude = √(269)
Direction = -37.57°
17. <2,-5>:
Magnitude = √(29)
Direction = -68.2°
18. <8,-4>:
Magnitude = √(80)
Direction = -26.57°
19. <-4.-6>:
Magnitude = √(52)
Direction = 56.3°
20. <-1,9>:
Magnitude = √(82)
Direction = -83.66°
We are asked to find the magnitude and direction of the vectors given as <x, y>. We have the formulas for magnitude and direction of the vectors.
Magnitude = √(x²+y²)
and direction, θ = tan⁻¹(y/x)
11. The vector is <0,4>
Magnitude = √(0²+4²) = 4
Direction = tan⁻¹(4/0) = tan⁻¹∞ = 90°
12. The vector is <-3,0>.
Magnitude = √(-3²+0²) = 3
Direction = tan⁻¹(0/-3) = tan⁻¹0 = 0°
13.The vector is <6,5>
Magnitude = √(6²+5²) = √(61)
Direction = tan⁻¹(5/6) = 39.8°
14. The vector is <3,7>
Magnitude = √(3²+7²) = √58
Direction = tan⁻¹(7/3) = 66.8°
15.The vector is <-2,1>
Magnitude = √(-2²+1²) = √5
Direction = tan⁻¹(1/-2) = -26.57°
16.The vector is <-10,13>
Magnitude = √(13²+-10²) = √(269)
Direction = tan⁻¹(-10/13) = -37.57°
17.The vector is <2,-5>
Magnitude = √(2²+-5²) = √(29)
Direction = tan⁻¹(-5/2) = -68.2°
18.The vector is <8,-4>
Magnitude = √(8²+-4²) = √(80)
Direction = tan⁻¹(-4/8) = -26.57°
19.The vector is <-4.-6>
Magnitude = √(-4²+-6²) = √(52)
Direction = tan⁻¹(-6/-4) = 56.3°
20. The vector is <-1,9>
Magnitude = √(-1²+9²) = √(82)
Direction = tan⁻¹(9/-1) = -83.66°
Learn more about magnitude and direction at https://brainly.com/question/2142917
#SPJ1
What is the fractional equivalent of 3.15?
Answers
Answer:
Below
Step-by-step explanation:
3.15 can be read as 3 and 15 hundredths = 3 15/100 = 3 3/20
Answer: 63/20
Step-by-step explanation:
Gravel is being dumped from a conveyor belt at a rate of 15 ft3/min, and its coarseness is such that it forms a pile in the shape of a cone whose base diameter and height are always equal. How fast is the height of the pile increasing when the pile is 12 ft high? (Round your answer to two decimal places.)
Answers
Answer:
0.13 ft/min
Step-by-step explanation:
We are given that
\(\frac{dV}{dt}=15ft^3/min\)
We have to find the increasing rate of change of height of pile when the pile is 12 ft high.
Let d be the diameter of pile
Height of pile=h
d=h
Radius of pile,r=\(\frac{d}{2}=\frac{h}{2}\)
Volume of pile=\(\frac{1}{3}\pi r^2 h=\frac{1}{12}\pi h^3\)
\(\frac{dV}{dt}=\frac{1}{4}\pi h^2\frac{dh}{dt}\)
h=12 ft
Substitute the values
\(15=\frac{1}{4}\pi(12)^2\frac{dh}{dt}\)
\(\frac{dh}{dt}=\frac{15\times 4}{\pi(12)^2}\)
\(\frac{dh}{dt}=0.13ft/min\)
Which function matches the data in the table
Answers
Answer:
I can't see the table...?
Step-by-step explanation:
I will answer if you have the table.
Find the area of a rectangle with base 2 yd and height 5 ft. (3 feet = 1 yard)
Answers
Answer:
30ft
Step-by-step explanation:
I am pretty sure. Please correct me kindly, if I am wrong.
Two pedestrians simultaneously left two villages 27 km apart and walked toward each other, meeting after 3 hours. The first pedestrian walked at a speed of 4 km per hour. At what speed (in km per h) did the second pedestrian walk?
Answers
The speed of the second pedestrian is 5 kilometers per hour.
At what speed did the second pedestrian walk?Let's say that the speed of the second pedestrian is S.
We know that the other pedestrian walks at a speed of 4km/h, and they (together) travel a distance of 27km in 3 hours, then we can write the linear equation:
(4km/h + S)*3h = 27km
It says that both pedestrians work, together, a total of 27km in 3 hours.
Now we can solve that linear equation for S, to do this, we need to isolate S in the left side of the equation.
4km/h + S = 27km/3h = 9 km/h
S = 9km/h - 4km/h = 5km/h
The speed of the second pedestrian is 5 kilometers per hour.
If you want to learn more about speed:
https://brainly.com/question/4931057
#SPJ1
Select the correct answer. Which expression is equivalent to the complex number 10 + 3i?
Answers
The expression that is equivalent to the complex number 10 + 3i is (4+7i)-2i(2+3i)
Complex numbersComplex numbers are square root of negative numbers. They are expressed as a + bi
Using the expression
(4+7i)-2i(2+3i)
Expand
4 + 7i - 4i -2i(3i)
4 + 3i - 2(-3)
4 + 6 + 3i
10 + 3i
Hence the expression that is equivalent to the complex number 10 + 3i is (4+7i)-2i(2+3i)
learn more on complex number here: https://brainly.com/question/10662770
#SPJ1

The expected probability of rolling an even number in 1 roll of a fair cube with faces numbered 1 through 6 is 1/2. When the cube was rolled 20 times, an even number came up 15 times, or 3/4 of the time. When the same cube was rolled 100 times, an even number came up 51 times, or almost 1/2 the time.
Why are the actual results closer to the expected probability of 1/2 when rolling the cube 100 times?
a. A larger sample size was used.
b. The 100 tosses were controlled better.
c. The expected probability changed when the cube was rolled 100 times.
d. The thrower considered only the even rolls, and disregarded the odd rolls.
Answers
Answer:
Step-by-step explanation:
The correct answer is a. A larger sample size was used.As per the Law of Large Numbers, the more times an experiment is repeated, the closer the actual results will be to the expected probability. In this case, rolling the cube 100 times provides a larger sample size than rolling it only 20 times. The more rolls that are made, the greater the likelihood that the actual results will converge towards the expected probability of 1/2 for rolling an even number.Option b, The 100 tosses were controlled better, is not relevant to this scenario since the fairness of the cube is assumed.Option c, The expected probability changed when the cube was rolled 100 times, is not true. The expected probability of rolling an even number on a fair six-sided die is always 1/2, regardless of the number of times it is rolled.Option d, The thrower considered only the even rolls, and disregarded the odd rolls, is not a valid assumption. The question states that the number of even rolls was recorded, but it does not imply that odd rolls were disregarded.
Find the slope-intercept form of the equation of the line that passes through the points AND graph
the line. (-3,5), (2,8)
Answers
Answer: y= 3/5x 6.8
Step-by-step explanation: The slope for these coordinates is 3/5 because the difference between 5 and 8 is 3, and the difference between -3 and 5 is 5. The y intercept is 6.8 because only with this y intercept the line goes through the points.

find 4 1/2% of 280 and round to the nearest tenth
Answers
Se sabe que la diagonal de un cuadrado mide 15 cm ¿cuánto mide su área?
Answers
Answer: 112.36cm^2
Step-by-step explanation:
Un cuadrado tiene 4 lados de igual longitud.
Si dibujamos la diagonal del cuadrado, podemos ver la imagen como dos triángulos rectángulos.
Donde los lados del cuadrado son los catetos, y la diagonal es la hipotenusa.
Ahora, recordando el teorema de Pitágoras, tenemos que, si A y B son catetos, y H es la hipotenusa:
A^2 + B^2 = H^2
En este caso sabemos que los catetos son iguales (por que es un cuadrado)
A = B.
Y también sabemos que H = 15cm.
A^2 + A^2 = (15cm)^2
2*A^2 = (15cm)^2
A = √((15cm)^2/2) = 15cm/√2 = 10.6 cm.
Ahora conocemos L, el largo de los lados de nuestro cuadrado.
L = 10.6cm
Y sabemos que el área de un cuadrado es igual a el cuadrado de uno de los lados:
Área = L^2 = (10.6cm)^2 = 112.36cm^2
Infinitely many solutions
-3x + y = 7
2x
-
Y
Y =
=
6x
3x
-
One solution
-
4y = -8
-4x
5
-4x + 1
-
y
= 4
2y = 8
0
No solution
Answers
Answer:
x=0
Step-by-step explanation:
How to find closing cost formula
Answers
Find the least common denominator for the fractions in the list.
8
7
15r5 12r3

Answers
Answer:
56
Step-by-step explanation:
Help me please find EC

Answers
The length of segment EC is 24 in the given triangle
A midsegment of a triangle is a segment that connects the midpoints of two sides of a triangle.
3x=2(x+4)
Apply distributive property on RHS
3x=2x+8
Subtract 2x from both sides
x=8
The segment EC =3x
=3(8)
=24
Hence, the length of EC is 24 in the given triangle
To learn more on Triangles click:
https://brainly.com/question/2773823
#SPJ1
There are 800 pupils at Stoke College in Years 7, 8 & 9 in total. There are 27% of them
in Year 7,38% in Year 8. How many pupils are in Year 9?
Answers
Answer:
280 pupils
Step-by-step explanation:
27 + 38 + x = 100 Find what percentage is the Year 9 which is 35%
800 x 0.35 = 280 pupils
write y+4=-2(x-1) in slope intercept form
Answers
Answer:
y=2x-6
Step-by-step explanation:
y+4=-2(x-1)
Since the slope intercept form is in the form of:
y=mx+c
Making above equation in this form.
y+4=-2(x-1)
opening bracket
y+4=2x-2
subtracting both side by 4.
y+4-4=2x-2-4
y=2x-6
This equation is the slope intercept form.
Risky drivers: An automobile insurance company divides customers into three categories: good risks, medium risks, and poor risks. Assume that of a total of 11,210 customers, 7761 are good risks, 2499 are medium risks, and 950 are poor risks. As part of an audit, one customer is chosen at random. Round youranswers to four decimal places if necessary.Part 1 of 2(a) What is the probability that the customer is a good risk?The probability that the customer is a good risk isXŚPart: 1/2Part 2 of 2(b) What is the probability that the customer is not a poor risk?The probability that the customer is not a poor risk isXŚ
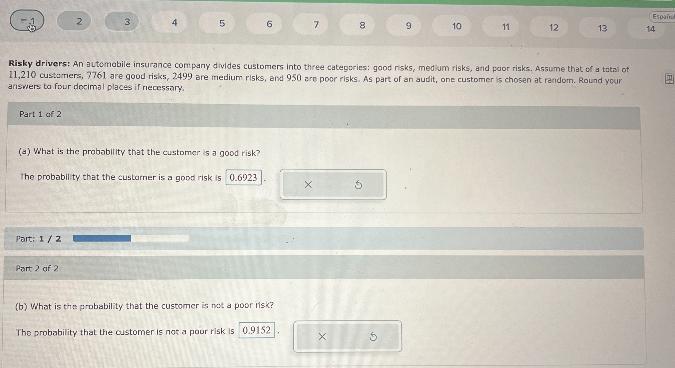
Answers
Given data:
Total: 11210
7761 good risk
2499 medium risk
950 poor risk
a) Probability of choose a customer with good risk (gr):
\(P(gr)=\frac{#customer\text{ }gr}{#total}=\frac{7761}{11210}=0.6923\)Th eprobability that the customer is a good risk is 0.6923b) Probability that a customer is not a poor risk (pr):
\(P(no\text{ }pr)=1-P(pr)=1-\frac{#custormer\text{ }pr}{#total}=1-\frac{950}{11210}=\frac{11210-950}{11210}=\frac{10260}{11210}=0.9153\)The probability that the customer is not a poor risk is 0.9153can anyone help me ??? pleassee on both of em

Answers
Answer:
28. B
29. D
30. A
Step-by-step explanation:
28.
2 5/8 yd × 5/6 yd =
= 21/8 × 5/6 yd²
= 105/48 yd²
= 35/16 yd²
= 2 3/16 yd²
Answer: B
29.
2641 becomes 6241.
In 6241, the 6 is in the thousands place.
6 × 1000 = 6000
Answer: D
30.
90 + 7 × (7 - 1) =
Use the correct order of operations.
= 90 + 7 × 6
= 90 + 42
= 132
Answer: A
(a) what is the probability that a randomly selected integer chosen from the first 100 positive integers is divisible by 3 or 5? are the two events (choosing an integer divisible by 3 and choosing an integer divisible by 5 randomly from the first 100 positive integers) independent?
Answers
The probability that a randomly selected integer from the first 100 positive integers is divisible by 3 or 5 is 47/100. The events of choosing an integer divisible by 3 and choosing an integer divisible by 5 are not independent.
To find the probability that a randomly selected integer from the first 100 positive integers is divisible by 3 or 5, we need to count the number of integers in this range that are divisible by 3 or 5, or both.
There are 33 integers in the range from 1 to 100 that are divisible by 3: 3, 6, 9, ..., 99. Similarly, there are 20 integers in this range that are divisible by 5: 5, 10, 15, ..., 100. However, some of these integers are divisible by both 3 and 5, which means we have counted them twice. To find the total number of integers that are divisible by 3 or 5, we need to subtract the number of integers that are divisible by both 3 and 5 (which are the multiples of 15):
33 + 20 - 6 = 47
So, there are 47 integers out of the first 100 positive integers that are divisible by 3 or 5.
To find out whether the two events of choosing an integer divisible by 3 and choosing an integer divisible by 5 are independent, we need to check whether the probability of one event changes if the other event has already occurred.
Let A be the event of choosing an integer divisible by 3, and B be the event of choosing an integer divisible by 5. We can find the probabilities of these events as follows:
P(A) = 33/100
P(B) = 20/100
To check for independence, we need to compare the probability of A given that B has occurred (i.e., the probability of choosing an integer divisible by 3, given that we know it is also divisible by 5) with the probability of A without any information about B:
P(A|B) = P(A and B) / P(B)
Since the multiples of 15 are the only integers that are divisible by both 3 and 5, we have:
P(A and B) = P(15) / 100 = 1/20
So,
P(A|B) = (1/20) / (20/100) = 1/4
This means that if we know an integer is divisible by 5, the probability that it is also divisible by 3 is 1/4.
Now, let's compare this with the probability of A without any information about B:
P(A) = 33/100
Since P(A|B) ≠ P(A), we can conclude that the events of choosing an integer divisible by 3 and choosing an integer divisible by 5 from the first 100 positive integers are not independent.
To know more about Probability:
https://brainly.com/question/11234923
#SPJ4
what is 11/4 times 4/9
Answers
Answer: 11/9
Step-by-step explanation:
you would cross out the two 4s(using butterfly method) and make them 1s. So 11 x 1 and 1 x 9 = 11/9
Answer:
11/4 times 4/9 is 11/9
Step-by-step explanation:
We have to find,
(11/4) times 4/9
\((11/4)(4/9) = (11*4/4*9)\)
We can cancel the 4s from the numeratorand denominator to get,
\((11*4/4*9) = (11*1/1*9) = 11/9\\=11/9\)
The answer is 11/9
URGENT PLEASE ANSWER. PHOTO OF PROBLEM ATTACHED. BRAINLIEST TO FIRST CORRECT ANSWER.

Answers
Answer:
27.23 inches
Step-by-step explanation:
question wants circumference over 2π/3 radians
2π/3 times 180/π = 120 degrees
120 is 1/3 of 360
so question wants 1/3 of the circumference
circumference is π times diameter
π times 26 = 81.6814089933
81.6814089933 divided by 3 =
27.2271363311 =
27.23
Find the complete factored form of the
polynomial :
-8m²n-7m² nª
Enter the correct answer.
Answers
The polynomial -8m²n - 7m²n can be factored using the common factor -m²n. The complete factored form of the polynomial is (-m²n) (8 + 7a).
To find the complete factored form of the polynomial -8m²n - 7m²n, we can factor out common terms from both the terms. The common factor in the terms -8m²n and -7m²n is -m²n. We can write the polynomial as:
-8m²n - 7m²n = (-m²n) (8 + 7a)
Therefore, the complete factored form of the polynomial -8m²n - 7m²n is (-m²n) (8 + 7a). This expression represents the original polynomial in a multiplied form. We can expand this expression using distributive law to verify that it is equivalent to the original polynomial.
For more such questions on polynomial, click on:
https://brainly.com/question/1600696
#SPJ8
Mathius walked ⅜ mile to school. Eva walked ⅖ mile to school. How many more
feet did Eva walk to school than Mathius? (1 mile = 5,280 feet). Explain how you
determined your answer using words and numbers.
Answers
Answer:
132ft
Step-by-step explanation:
Mathius Distance = 3/8 mile
Eva Distance = 2/5 mile
1 mile = 5,280ft
1. Start by multiplying the mile distance of Mathius to the distance of 1 mile in feet.
5,280ft x 3/8 = 15840ft/8 = 1980ft
2. Do the same thing as number 1 but for Eva's distance now.
5,280ft x 2/5 = 10560ft/5 = 2112ft
3. Subtract Eva's Distance from Mathius' Distance for the answer.
2112ft (Eva) - 1980ft (Mathius) = 132ft
Beverly has a bag of marbles that weighs 30 grams. She knows that each marble weighs 1.5 grams and the bag weighs 1.5 grams. Which equation could she use to determine how many marbles are in the bag? Select all that apply. (1.5)x + 1.5 = 30 30 – x = 2(1.5) (1.5)(30) = 1.5x 1.5 + x = 30 1.5x = 30 – 1.5
Answers
Answer:
1.5x = 30 - 1.5
Step-by-step explanation:
30 grams minus the weight of the bag 1.5
1.5x x is the number of marbles and the bag so take 1 out and you have an answer which is 28.5 19 marbles
Find the consumers surplus

Answers
The consumer surplus is approximately $145.83.
To find the consumer surplus, we first need to find the demand function's inverse, which gives us the willingness to pay for each unit of the product. The demand function is:
D(x) = √(739 - 3x)
Setting D(x) equal to the equilibrium price of $25, we get:
25 = √(739 - 3x)
Squaring both sides, we get:
625 = 739 - 3x
Solving for x, we get:
So at a price of $25 per unit, the consumer is willing to buy 38 units per month.
Now we can calculate the consumer's surplus.
The consumer\(x = (739 - 625) / 3 = 38\) surplus is the difference between the total amount that consumers are willing to pay for a certain quantity of a good and the total amount they actually pay. In this case, the consumer's surplus can be calculated as:
\(CS = \int_0^{38} [D(x) - 25] dx\)
where D(x) is the demand function, and the integral is taken over the range of 0 to 38, which represents the quantity demanded at a price of $25 per unit.
Evaluating this integral, we get:
\(CS = \int_0^{38} [\sqrt{(739 - 3x)} - 25] dx\\\\= [1/6 (739 - 3x)^{(3/2)} - 25x]_0^{38}\\\\= \$ 145.83\)
Therefore, the consumer surplus is approximately $145.83.
Learn more about function here:
https://brainly.com/question/29633660
#SPJ1
A job has a normal time of 12 minutes, a performance rating of 0.80, and an allowance of 20 percent of job time. The standard time for this job in minutes is:_______
a. 11.52.
b. 12.
c. 14.4.
d. 15.
e. depends on the number of cycles observed.
Answers
Solution :
The standard time for doing a job in minutes is given by :
Standard time = Normal time + normal time x allowance factor.
Here, it is given that ,
Allowance factor = 20%
= 0.20
Normal time of doing a a job = 12 minutes.
Therefore,
Standard time = Normal time + normal time x allowance factor
Standard time = 12 + 12 x 0.20
= 12 + 2.4
= 14.4
Thus, the standard time for doing the job is 14.4 minutes.
At a baseball game, a vender sold a combined total of 191 sodas and hot dogs. The number of hot dogs sold was 47 less than the number of sodas sold. Find the number of sodas sold and the number of hot dogs sold.
Answers
The number of sodas sold at the baseball game was 119, while the number of hot dogs sold was 72.
Let's assume the number of sodas sold as 'x' and the number of hot dogs sold as 'y'.
According to the problem, the total number of sodas and hot dogs sold is 191, so we can write the equation:
x + y = 191 ...(1)
The problem also states that the number of hot dogs sold was 47 less than the number of sodas sold. Mathematically, we can express this as:
y = x - 47 ...(2)
To find the values of x and y, we can solve the system of equations (1) and (2). Substituting equation (2) into equation (1), we have:
x + (x - 47) = 191
Simplifying the equation:
2x - 47 = 191
2x = 191 + 47
2x = 238
Dividing both sides by 2:
x = 238/2
x = 119
Substituting the value of x back into equation (2):
y = 119 - 47
y = 72
As a result, the total amount of sodas sold is 119, and the total amount of hot dogs sold is 72.
For more such questions on number, click on:
https://brainly.com/question/24644930
#SPJ8