An object moves in simple harmonic motion with period 8 minutes and amplitude 12m. At time =t0 minutes, its displacement d from rest is −12m, and initially it moves in a positive direction.
Give the equation modeling the displacement d as a function of time t
Answers
An object moves in simple harmonic motion with a period of 8 minutes and an amplitude of 12 m. At time =t0 minutes, its displacement d from rest is −12m, and initially, it moves in a positive direction. We can write the final equation for the displacement d as a function of time t: d(t) = 12 * cos((π/4)t + π)
To model the displacement d as a function of time t for an object in simple harmonic motion with a period of 8 minutes and an amplitude of 12m, we'll use the following equation:
d(t) = A * cos(ωt + φ)
where:
- d(t) is the displacement at time t
- A is the amplitude (12m in this case)
- ω is the angular frequency, calculated as (2π / period)
- t is the time in minutes
- φ is the phase angle, which we'll determine based on the initial conditions
Since the period is 8 minutes, we can calculate the angular frequency as follows:
ω = (2π / 8) = (π / 4)
At t = 0 minutes, the displacement is -12m, and the object moves in a positive direction. So we have:
-12 = 12 * cos(φ)
Dividing both sides by 12:
-1 = cos(φ)
Therefore, φ = π (or 180°) since the cosine of π is -1.
Learn more about simple harmonic motion: https://brainly.com/question/26114128
#SPJ11
Related Questions
Please help ASAP, I need to answer this by the end of the day I need really need help!!!

Answers
Answer:
1. I believe some solutions could be x= -7, x= -8, x= -9 etc.
Step-by-step explanation:
2. If the inequality was -3x is greater than or equal to 18 then x and also be equal to x=6.
F(x, y)=x^2-6xy-2y^3
find the critical points of the
given functions and classify each as a relative
maximum, a relative minimum, or a saddle point
Answers
The one critical point at (0, 0).
The critical point (0, 0) is a saddle point, and the critical point (-9, -3) is a relative minimum.
To find the critical points of the given function f(x, y) = x^2 - 6xy - 2y^3, we need to find the points where the partial derivatives with respect to x and y are equal to zero.
Calculate the partial derivative with respect to x (f_x):
f_x = 2x - 6y
Calculate the partial derivative with respect to y (f_y):
f_y = -6x - 6y^2
Set both partial derivatives equal to zero and solve the system of equations:
2x - 6y = 0 ---(1)
-6x - 6y^2 = 0 ---(2)
From equation (1), we can rearrange it to solve for x:
2x = 6y
x = 3y
Substituting x = 3y into equation (2):
-6(3y) - 6y^2 = 0
-18y - 6y^2 = 0
-6y(3 + y) = 0
Now, we have two possible cases:
a) -6y = 0
b) 3 + y = 0
a) -6y = 0
This implies y = 0
Substituting y = 0 into equation (1):
2x - 6(0) = 0
2x = 0
x = 0
So, we have one critical point at (0, 0).
b) 3 + y = 0
This implies y = -3
Substituting y = -3 into equation (1):
2x - 6(-3) = 0
2x + 18 = 0
2x = -18
x = -9
So, we have another critical point at (-9, -3).
Now, to classify each critical point as a relative maximum, relative minimum, or a saddle point, we need to analyze the second-order partial derivatives.
Calculate the second partial derivative with respect to x (f_xx):
f_xx = 2
Calculate the second partial derivative with respect to y (f_yy):
f_yy = -12y
Calculate the mixed partial derivative (f_xy):
f_xy = -6
Now, evaluate the discriminant D = f_xx * f_yy - (f_xy)^2 at each critical point:
For the critical point (0, 0):
D = f_xx * f_yy - (f_xy)^2
= 2 * (-12 * 0) - (-6)^2
= 0 - 36
= -36
For the critical point (-9, -3):
D = f_xx * f_yy - (f_xy)^2
= 2 * (-12 * -3) - (-6)^2
= 72 - 36
= 36
Analyzing the discriminant:
For the critical point (0, 0):
If D < 0, it is a saddle point. In this case, D = -36, so (0, 0) is a saddle point.
For the critical point (-9, -3):
If D > 0 and f_xx > 0, it is a relative minimum. In this case, D = 36 and f_xx = 2, so (-9, -3) is a relative minimum.
Therefore, the critical point (0, 0) is a saddle point, and the critical point (-9, -3) is a relative minimum.
To learn more about discriminant, refer below:
https://brainly.com/question/15884086
#SPJ11
1/4 divided by 1/13 please help !
Answers
Answer:
13/4
Step-by-step explanation:
We do reciprocal of 1/13 it will be 13/1 after we multiply last answer 13/4
Answer:
3 1/4
Step-by-step explanation:
\( \frac{1}{4} \div \frac{1}{13} \\ \\ = \frac{1}{4} \times \frac{13}{1} \\ \\ = \frac{1 \times 13}{4 \times 1} \\ \\ = \frac{13}{4} \\ \\ = 3 \frac{1}{4} \\ \)
SIMPLIFY
STEP BY STEP EXPLANATION
WILL MARK BRAINLIEST!!!!!!!!!!!!!

Answers
Answer:
3x+7
3
Step-by-step explanation:
(3x-7) × (3x+7) × ____2x+4_____
6 3x∧2-x-14
(3x-7) × (3x+7) × ____2(x+2)_____
6 3x∧2 × 6x-7x-14
(3x-7) × (3x+7) × _____x+2_______
3 3x × (x+2)-7(x+2)
(3x-7) × (3x+7) × _____ x+2_______
3 (x+2) × (3x-7)
3x+7
3
Hope this helps! :)
Please help me with edge question .

Answers
\(~\hspace{7em}\textit{negative exponents} \\\\ a^{-n} \implies \cfrac{1}{a^n} ~\hspace{4.5em} a^n\implies \cfrac{1}{a^{-n}} ~\hspace{4.5em} \cfrac{a^n}{a^m}\implies a^na^{-m}\implies a^{n-m} \\\\[-0.35em] ~\dotfill\\\\ (4)^{\frac{-4}{2}} \implies (4)^{-2}\implies 4^{-2}\implies \cfrac{1}{4^2}\implies \cfrac{1}{16}\)
Find the volume of the hemisphere.

Answers
Answer:
Use this image for help and reference
Hopefully this helps:)

THE FORMULAE OF HEMISPHERE : V = 2/3 * π * r³
Step-by-step explanation:
Put the formulae of hemisphere,
V = 2/3 * π * r³
Put the values in the formulae,
= 2/3 × 3.14 × 9³
= 0.6666 × 3.14 × 729
= 2.09312× 729
= 1525.8m³ ans
→ value of π (pie) is 3.14
→ formulae of radius is d/2 = 18/2 = 9 in
Please help‼️ domain and range‼️ also look at image please

Answers
The range is (-infinity, 0) U (0, infinity)
not every linearly independent set in set of real numbers r superscript ℝn is an orthogonal set. T/F?
Answers
The given statement is true.
Consider linearly independent vectors of \(R_{n}\)
Where n = 2
\(V = \[\begin{array}{ccc}4&\\2\end{array}\right]\)
\(U = \[\begin{array}{ccc}5&\\6\end{array}\right]\)
Now product of these vectors
UV = 4x5 + 2x6
= 32
Hence these vectors are not orthogonal.
To learn more about linearly independent vectors visit:
https://brainly.com/question/31328368
#SPJ1
what is the equation of the function that is graphed as line a?

Answers
here we can clearly see that the graph intersect both the x-axis and y-axis at points mention below :
{ (3,0),(0,-1),(-3,-2),(-6,-3),(6,1) }
we need to check these points for each equation whether they satisfy or not.
now we consider the first equation--
y=3x-1on putting points (3,0) in equation first
0=3*3-1 (not correct)
now we consider second equation--
y=3x+1on putting points (3,0) in equation second
0=3*3+1 (not correct)
now we consider third equation--
y=(1/3*x)-1on putting points (3,0) in third equation
0=(1/3*3)-1 results(0=0)(correct)
checking point(0,-1) on third equation
-1=(1/3*0)-1 result(-1= -1)(correct)
checking point(-3,-2) on third equation
-2=1/(3*-3)-1 results(-2= -2)(correct)
checking point(-6,-3) on third equation
-3=1/(3*-6)-1 results(-3= -3)(correct)
checking point(6,1) on third equation
1=1/(3*6)-1 results(1=1)(correct)
now we consider fourth equation-----
y= -1/3*x+1checking point(3,0)
0= - 1/3*3+1 result (0=0)(correct)
checking for point (0,-1)
-1=-1/3*0+1 (not correct)
now we can clearly say that only third equation satisfied all the points
so third equation is the function that is graphed as line a.
to learn more about function of graph
brainly.com/question/24335034
Can someone please explain Pythagoras theorem !
Answers
Answer: phythagorean therorem??
Step-by-step explanation:
a^2 + b^2 = c^2
does that help or do you need more help?
What is the volume of the given cone?
9 ft
8 ft
Show all the steps starting from the formula.
Answers
Answer:
we have
radius[r]=9ft
height [h]=8ft
now
Volume of cone =1/3×πr²h=1/3×π×9²×8=678.584ft³
If 5x kilos of carrots cost php 900.00 pesos, how much is the price per kilo?
Answers
Answer:
180 pesos
Step-by-step explanation:
divide 900 by 5
True or False: The margin of error is to account for biased sampling methods.
Answers
Answer:
Step-by-step explanation:
tru i took the test
PLEASEE HELPP 100 POINTS
Jonny is writing a program for a video game. For one part of the game he uses the rule given below to move objects on the screen.
Showing all your work, give the output that the rule gives for the inputs.
(x, y)→(x−7.5, y+6.8)
First input: (4.3, 3.5)
Second input: (8.2, -3.2)
Answers
Answer:
The first input (-3.2, 10.3)..... 2nd input (0.7, 3.6)
Step-by-step explanation:
The first input: 4.3 - 7.5 = -3.2 = the x
(-3.2, 10.3) 3.5 + 6.8 = 10.3 = the y
The 2nd input:
8.2 - 7.5 = 0.7 . = the x
(0.7, 3.6) -3.2 + 6.8 = 3.6 = the y
Mark brainliest if this helped! <3
I need help on this quesion. (Easy)

Answers
Answer:
the answer is C
Step-by-step explanation:
just divide 42.75 by 9
I'm not 100% sure on how to figure out this equation, can can anyone help out?

Answers
Answer:
Aonnalin, great name :) answer as below
Step-by-step explanation:
They tell us to use slope-intercept form. This is something you will just have to remember y = mx+b
It is confusing b/c there is the other one, the point-slope formula too. but just remember both and know that the point-slope one is to get to the slope-intercept one. y-y1 = m(x-x1)
m= slope
m = (y2-y1) / (x2-x1)
P1= (0,7) in the form (x1,y1)
P2 =(8,-2) in the form (x2,y2)
m = -2-7 / 8-0
m = -9 / 8
now that we have the slope, just use either point with the point-slope
y-7 = (-9/8)(x-0)
y-7 = -9x/8
y = -9x/8 + 7
y = \(\frac{-9}{8}\) X + 7
slope-intercept form :)
The price of a coat is reduced by 15% in a sale.
The sale price of the coat is £136.
Work out the price of the coat before the sale.
Answers
Step-by-step explanation:
Find 100% of the price:
100 - 15 = 85% (Sale price)
85% = 136
1% = 136 divide 85 = 1.6
100% = 1.6 x 100 = 160
Ans: £160
WHICH GRAPH SHOWS THE SOLUTIONS?

Answers
The graph of the inequality is the third one, counting from the top.
Which graph shows the solution set of the inequality?Here we have the following inequality:
(1/2)n + 3 < 5
First we need to isolate the variable, we will get:
(1/2)n + 3 < 5
(1/2)n < 5 - 3
(1/2)n < 2
n < 2*2
n < 4
So we will have an open circle at n = 4, and an arrow that goes to the left (because n is smaller than 4).
Then the correct number line is the third one, counting from the top.
Learn more about inequalities:
https://brainly.com/question/24372553
#SPJ1
Sorry but need help again! 10 points and if two people answers brainiest goes to first!! :)

Answers
Answer:
B. Domain is left to right so the left point is solid on 2 and the right is solid on 8. The solid point means it can also be equal to.
Answer:
B) {x : 2 \(\leq\) x \(\leq\) 8 }
Step-by-step explanation:
The function of the graph's x values are between 2 and 8, but the dots at the ends of the function are closed, hence the answer is
2 \(\leq\) x \(\leq\) 8
type the correct answer in the box. The formula for the volume, V, of a cone having the radius, r, and the height, h, is shown below. Write the formula to calculate the height, h.
Answers
Answer:
You have to make h the subject using volume of cone formula :
\(v = \frac{1}{3} \times \pi \times {r}^{2} \times h\)
\(3v = \pi {r}^{2} \times h\)
\( \frac{3v}{\pi {r}^{2} } = h\)
\(h = \frac{3v}{\pi {r}^{2} } \)
Anyone wanna help me do this because I’m not understanding how this works
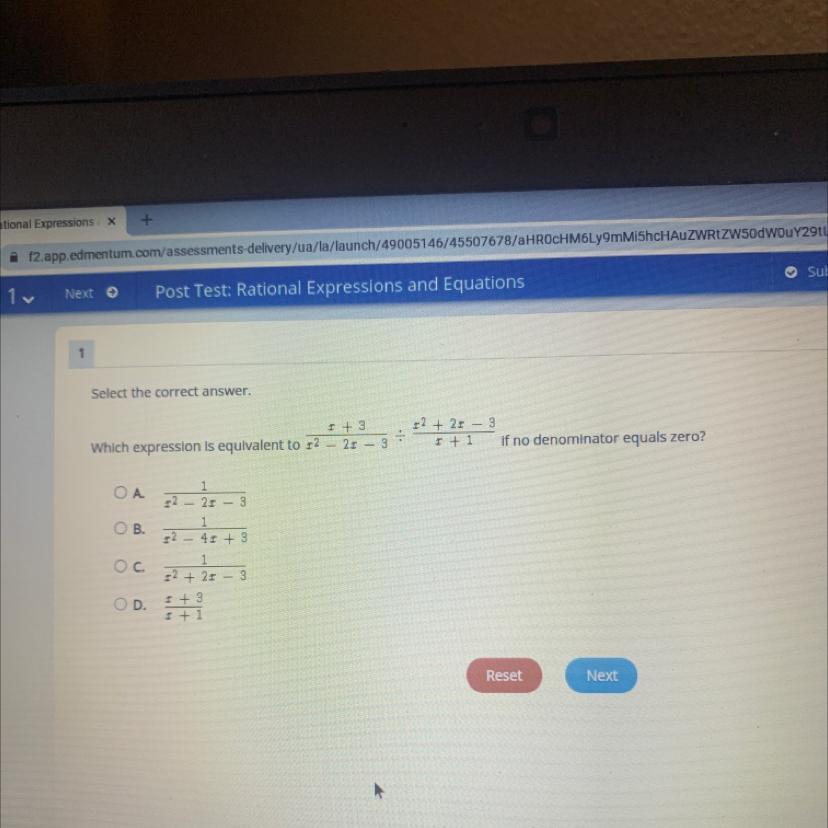
Answers
Answer:
its b .
Step-by-step explanation:
See the Pic for my question.

Answers
Answer:
C. 7
Step-by-step explanation:
4 * Sum (i = 1 to 3) (1/2)^(i - 1) =
= 4 * [(1/2)^0 + (1/2)^1 + (1/2)^2]
= 4 * [1 + 1/2 + 1/4]
= 4 * [7/4]
= 7
Answer:
7
Step-by-step explanation:
because I'm smart like that
the square mil area for a 2 inch wide by 1/4 inch thick copper busbar = ? square mils.
Answers
The square mil area for a 2 inch wide by 1/4 inch thick copper busbar is 500 square mils.
How to find the square mil area of a copper busbar?To find the square mil area for a 2 inch wide by 1/4 inch thick copper busbar, we need to multiply the width and thickness of the busbar in mils.
1 inch = 1000 mils
So, the width of the busbar in mils = 2 inches x 1000 mils/inch = 2000 mils
And, the thickness of the busbar in mils = 1/4 inch x 1000 mils/inch = 250 mils
Therefore, the square mil area of the copper busbar = width x thickness = 2000 mils x 250 mils = 500,000 square mils.
Hence, the square mil area for a 2 inch wide by 1/4 inch thick copper busbar is 500,000 square mils.
Learn more about cross-sectional area
brainly.com/question/20532494
#SPJ11
A pretzel recipe calls for 3.325
cups of flour. If the recipe makes
9.5 pretzels, how many cups of
flour are need for each pretzel?
Answers
Answer: 0.35
Step-by-step explanation:
3.325 divided by 9.5 = 0.35
find the aspect ratio/length of a ping pong table which is 108 inches long and five feet wide
Answers
The aspect ratio/length of a ping pong table which is 108 inches long and five feet wide is 1.8
What is an equation?An equation is an expression that shows the relationship between two or more numbers and variables.
An independent variable is a variable that does not depend on other variables while a dependent variable is a variable that depends on other variables.
Length = 108 inches, width = 5 ft = 60 in
Aspect ratio = longer dimension / shorter dimension = 108 in / 60 in = 1.8
The aspect ratio/length of a ping pong table which is 108 inches long and five feet wide is 1.8
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
consider the unit circle (circle of radius 1 centered at the origin) in r2. is h a subspace of r2 or not? explain your reasoning
Answers
H does not satisfy all three properties required for a subspace, we can conclude that H is not a subspace of R2.
The set H is a subspace of R2, we need to check if it satisfies the three properties required for a subspace
1. The zero vector is in H.
2. H is closed under vector addition.
3. H is closed under scalar multiplication.
Now each property
1. The zero vector (0, 0) is in H since it lies on the unit circle.
2. To check closure under vector addition, suppose we have two vectors (x₁, y₁) and (x₂, y₂) in H. If we add them together, (x₁, y₁) + (x₂, y₂), the resulting vector will not necessarily lie on the unit circle. For example, if we add (1, 0) and (-1, 0), the result is (0, 0), which is not on the unit circle. Therefore, H is not closed under vector addition.
3. To check closure under scalar multiplication, suppose we have a scalar c and a vector (x, y) in H. If we multiply them, c × (x, y), the resulting vector will not necessarily lie on the unit circle. For example, if we multiply (1, 0) by 3, the result is (3, 0), which is not on the unit circle. Therefore, H is not closed under scalar multiplication.
Since H does not satisfy all three properties required for a subspace, we can conclude that H is not a subspace of R2.
To know more about subspace click here :
https://brainly.com/question/30318872
#SPJ4
find volume of region bounded by z = x2 y2 and z = 10 - x2 - 2y2
Answers
The volume of region bounded by z = x2 y2 and z = 10 - x2 - 2y2 is ∞.
To find the volume of the region bounded by the surfaces z = x^2 y^2 and z = 10 - x^2 - 2y^2, we can use triple integrals in cylindrical coordinates.
First, we need to find the limits of integration.
The surfaces intersect at the boundary where z = x^2 y^2 = 10 - x^2 - 2y^2.
Rearranging the equation gives us x^2 + 2y^2 + x^2 y^2 - 10 = 0.
This can be factored as (x^2 + 1)(y^2 + 2) - 12 = 0.
Thus, we have two curves: x^2 + 1 = 0 and y^2 + 2 = 0.
However, neither curve is possible because we cannot take the square root of a negative number.
Therefore, there is no boundary and the region is unbounded.
To set up the triple integral,
we can use cylindrical coordinates: x = r cos(θ), y = r sinθ), and z = z.
The Jacobian is r, so the volume is given by:
V = ∫∫∫ r dz dr dθ
The limits of integration for r and θ are 0 to infinity and 0 to 2π, respectively.
The limit for z is from the surface z = x^2 y^2 to z = 10 - x^2 - 2y^2.
However, since there is no boundary, we can integrate from z = 0 to z = infinity.
Thus, we have:
V = ∫∫∫ r dz dr dθ from 0 to infinity for z, 0 to infinity for r, and 0 to 2π for theta.
Evaluating the integral gives us:
V = ∫0^2π ∫0^∞ ∫0^∞ r dz dr dθ = ∞
Therefore, the volume of the region bounded by the surfaces z = x^2 y^2 and z = 10 - x^2 - 2y^2 is infinity.
Learn more about triple integrals in cylindrical coordinates : https://brainly.com/question/31405517
#SPJ11
how many ways are there to assign each of $6$ friends to either the chemistry class or the biology class if one of these six, manoj, refuses to be in a class without any of his friends?
Answers
There are 62 number of ways in which classes to these students can be assigned. It can be solved by using the fomula of combination.
What is the formula of combination?
Following is the fomula of combination:
\(^nC_r=\frac{n!}{r!(n-r)!}\)
Here, n is the total objects available and r is the number of object need to choose from n objects.
Let six friends are A, B, C, D, E, and manoj.
Consider all 6 friends are in chemistry class. Hence, number of ways in which it can be is,
\(^6C_6\)
Consider 5 friends are in chemistry class. Hence, number of ways in which it can be is,
\(^6C_5\)
Consider 4 friends are in chemistry class. Hence, number of ways in which it can be is,
\(^6C_4\)
Consider 3 friends are in chemistry class. Hence, number of ways in which it can be is,
\(^6C_3\)
Consider 2 friends are in chemistry class. Hence, number of ways in which it can be is,
\(^6C_2\)
Consider 1 friend is in chemistry class. Hence, number of ways in which it can be is,
\(^6C_1\)
Consider no friend is in chemistry class all are in biology class. Hence, number of ways in which it can be is,
\(^6C_0\)
Hence, total number of ways in which classes can be assigned to 6 students is,
\(^6C_6+^6C_5+^6C_4+^6C_3+^6C_2+^6C_1+^6C_0=64\)
Now, the number of ways in which mnoj is alon. There are two ways. Either he will be in the chemistry class or he will be in the physics class.
Hence, subtract 2 from 64 to get the answer.
\(64-2=62\)
Hence, there are 62 number of ways in which classes to these students can be assigned.
Learn more about combination from the following link:
https://brainly.com/question/11732255
#SPJ4
what is the rectangular form of 6(cos(225o) i sin(225o))? negative 3 startroot 2 endroot minus 3 startroot 2 endroot i negative 3 startroot 2 endroot 3 startroot 2 endroot i 3 startroot 2 endroot minus 3 startroot 2 endroot i
Answers
The rectangular form of 6{(cos225°) +i(sin225°) }is -3√2-3i√2.The shape that complex numbers typically take is referred to as rectangle form: z = a + bi.
What are polar form and rectangular form?Polar notation depicts a complex number in terms of the lengths of the vector and the angular direction from the starting point. In rectangle notation, a complex number is represented by its vertical and horizontal dimensions. The system is referred to be rectangular because the angles made by the axes at the origin and the measurements at point p are both 90 degrees. As a result, the measurement results in a rectangle with sides Xp and Yp.
To determine rectangular form, we obtain,
Let Z=6{(cos225°) +i(sin225°)}
Now, cos225°=-cos( 180°+45°)= -cos45°= -\(\frac{1}{√2}\)
sin225°=-\(\frac{1}{√2}\)
S0, 6{(cos225°) +i(sin225°)}= 6 ( -\(\frac{1}{√2}\))+6i(-\(\frac{1}{√2}\))=-3√2-3i√2.
To know more about rectangular form visit:
https://brainly.com/question/29550350
#SPJ1
Answer:
A
Step-by-step explanation:
right on edge
ll
Gina is making a square tablecloth.
54 in.
How much fabric will Gina need?
Answers
Answer:13.5
Step-by-step explanation:
13.5