An is a mathematical statement that shows two expressions are equal using an equal sign.
Answers
No! Because a mathematical statement is actually a statement that is either true or false not a statement that shows two expressions are equal using an equal sign!
Answer:
fix the awser
Step-by-step explanation:
Related Questions
state the domain and range for the following relation. then determine whether the relation represents a function.
Answers
The domain and range need to be determined for a given relation, and it will be determined whether the relation represents a function.
To determine the domain and range of a relation, we need to examine the set of inputs (domain) and the set of corresponding outputs (range). The domain is the set of all possible input values for which the relation is defined, while the range is the set of all possible output values that result from the given inputs.
In the context of determining whether the relation represents a function, we need to ensure that each input value from the domain corresponds to a unique output value. If there is any input value that produces multiple output values, the relation is not a function.
To determine the domain, we examine the set of all valid input values. This can be based on restrictions or limitations stated in the problem or the nature of the relation itself. The range, on the other hand, is determined by observing the set of all output values that result from the given inputs.
Once the domain and range are determined, we can check if each input in the domain corresponds to a unique output in the range. If every input has a unique output, the relation represents a function. If there is any input that maps to multiple outputs, the relation does not represent a function.
To know more about function refer here:
https://brainly.com/question/17440903
#SPJ11
Unless specified, all approximating rectangles are assumed to have the same width. Evaluate the upper and lower sums for f(x) = 1 + cos cos($) -ISXS*, with n = 3, 4, and 6. Illustrate each case with a sketch similar to the figure shown below. (Round your answers to two decimal places.) n = 3: upper sum ll lower sum n = 4: upper sum II lower sum n = 6: upper sum IO lower sum
Answers
In this Trigonometric Functions F(x) = 1 + cos(1/X): n=3 (12.01, 8.10), n=4 (11.65,8.50), and n=6 (11.24, 9.12), with their upper and lower value
What is Trigonometric Functions?
Trigonometry uses six fundamental trigonometric operations. Trigonometric ratios describe these operations. The sine function, cosine function, secant function, co-secant function, tangent function, and co-tangent function are the six fundamental trigonometric functions. The ratio of sides of a right-angled triangle is the basis for trigonometric functions and identities. Using trigonometric formulas, the sine, cosine, tangent, secant, and cotangent values are calculated for the perpendicular side, hypotenuse, and base of a right triangle.
F(x) = 1 + cos(1/X)
for n=3
Upper sum = 12.01
Lower sum = 8.10
Δx = (b-a)/n = 2π / 3
for n=4
Upper sum = 11.65
Lower sum = 8.50
Δx = (b-a)/n = π / 2
for n=6
Upper sum = 11.24
Lower sum = 9.12
Δx = (b-a)/n = π / 3
Hence, n=3 (12.01, 8.10), n=4 (11.65,8.50), and n=6 (11.24, 9.12), with their upper and lower value.
Learn more about Trigonometric Functions, by the following link.
https://brainly.com/question/25618616
#SPJ4
Find the measure of.. (image included)
I need help please! My teacher changed the due date to today and I don't understand it.

Answers
Answer:
B) 50
Step-by-step explanation:
<A = x + 53
x + 53 + x + 83 + 50 = 180
2x + 186 = 180
2x = -6
x = -3
<A = x + 53
-3 + 53
50
What is the domain of the function?
What is the range of the function?
( please explain briefly!! i have no idea how to this )
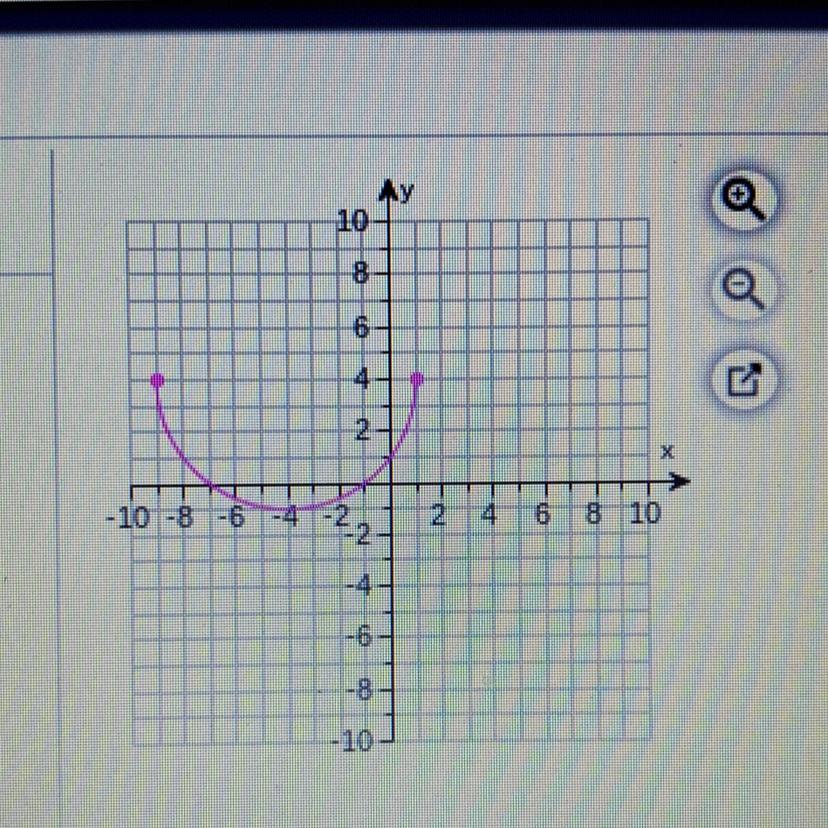
Answers
Answer:
Domain = [-9, 1]
Range = [-1, 4]
Step-by-step explanation:
The horizontal extent of the graph is from - 9 to 1. Therefore,
Domain = [-9, 1]
The vertical extent of the graph is from - 1 to 4. Therefore,
Range = [-1, 4]
Two friends, Jordan and Nicole, took summer jobs. Nicole earned $208.80 in 8 hours. The table below represents Jordan's earnings in dollars and cents, y, for working x hours.
Answers
26.1 would be your answer, i THINK. considering you didn't add the table ;-;
Answer:$29.60
Step-by-step explanation:
The table below shows Nicole's earnings on the job.
\text{Time (hours)}Time (hours) \text{Earnings (dollars)}Earnings (dollars)
1010 \$296$296
2222 \$651.20$651.20
2424 \$710.40$710.40
\text{What is Nicole's rate of pay, in dollars per hour?}
What is Nicole’s rate of pay, in dollars per hour?
\text{Rate}=
Rate=
\,\,\frac{\text{Dollars}}{\text{Hours}}
Hours
Dollars
\text{Rate}=
Rate=
\,\,\frac{296}{10}
10
296
\text{Rate}=
Rate=
\,\,29.6
29.6
\text{We get the same rate of pay for every pair:}
We get the same rate of pay for every pair:
\text{Time (hours)}Time (hours) \text{Earnings (dollars)}Earnings (dollars) \text{Rate}Rate
1010 \$296$296 \frac{\$296}{10}=29.6
10
$296
=29.6
2222 \$651.20$651.20 \frac{\$651.20}{22}=29.6
22
$651.20
=29.6
2424 \$710.40$710.40 \frac{\$710.40}{24}=29.6
24
$710.40
=29.6
\text{Nicole's rate of pay is \$29.60 per hour.}
Nicole’s rate of pay is $29.60 per hour.
This is the same as the constant of proportionality between earnings and time.
What is 45.5% in simplest form?
Answers
Answer: 45.5/100 = 455/1000
Step-by-step explanation:
Step-by-step explanation:
45.5% in its simplest form is
\( \frac{91}{2} \)
but 45.5% =
\( \frac{91}{2} \ \times 100 = \frac{91}{200} \)
A random sample of 100 automobile owners shows that in the state ofVirginia, an automobile is driven on the average 23,500 kilometersper year with a standard deviation of 3900 kilometers.
b) What can we assert with 99% confidence about the possible sizeof error if we estimate the average number of kilometers driven bycar owners in Virginia is to be 23500 per year?
Answers
Based on the information provided, we can assert with 99% confidence that the possible size of error in estimating the average number of kilometers driven by car owners in Virginia to be 23,500 kilometers per year is within a range of +/- 774.14 kilometers. This is calculated using the formula:
Margin of error = z-score x (standard deviation / square root of sample size)
Where the z-score for a 99% confidence level is 2.576. Plugging in the values, we get:
Margin of error = 2.576 x (3900 / square root of 100)
Margin of error = 2.576 x 390
Margin of error = 1004.64 / 2
Margin of error = +/- 774.14
Therefore, we can assert that the estimated average number of kilometers driven by car owners in Virginia is within a range of 22,725.86 kilometers to 23,274.14 kilometers with 99% confidence.
Learn more about error here:
https://brainly.com/question/19575648
#SPJ11
Two yards of fabric costs $15. Find the cost
for 7 yards of fabric if the cost of fabric
varies directly with the number of yards.
Answers
creí que son 21
Step-by-step explanation:
5$--3-$+3+&$73+3-+$
Oh so you like math name every digit in pi
Answers
did you mean name every flavor of pie
what is the value halp me

Answers
Answer- This is a fairly simple calculation, I got a -1/5,
Step-by-step explanation:
This is the way solved it, just substitute the x value for 1, and just solve. Hope it helps.
.........,..........
Formula for finding the selling price and cost price.
Sales tax is given, its either a whole number or a percentage.
Answers
Answer:
All formulae about profit and loss:-
A) Gain = SP – CP
B) Loss = CP –SP
C) Loss or gain is always calculated over CP.
D) %Gain = {(Gain*100)/CP}
E) %Loss = {(Loss*100)/CP}
F) SP = {(100 %Gain)/100}*CP
G) SP = {(100-%Loss)/100}*CP
H) CP = {100/(100 %Gain)}*SP
I) CP ={100/(100-%Loss)}*SP
J) If an article is sold at a gain of say, 20%, then SP = 120% of CP.
K) If an article is sold at a loss of say, 20%, then SP = 80% of CP.
hope it helps :)
\( \frac{100 + gain\%}{100} \times cost \: \: price\)
Selling price =\( \frac{100 - loss\%}{100} \times cost \: \: price\)
Cost price =\(\frac{100}{100 + gain\%} \times selling \: \: price\)
Cost price =\(\frac{100}{100 - loss\%} \times selling \: \: price\)
Hope you could get an idea from here.
Doubt clarification - use comment section
pls help!!!
math
what the value??
--

Answers
\(\qquad\qquad\huge\underline{{\sf Answer}}\)
Here we go ~
\(\qquad \sf \dashrightarrow \: \sqrt{ - 25} \)
\(\qquad \sf \dashrightarrow \: \sqrt{ - 1 \times 25} \)
\(\qquad \sf \dashrightarrow \: \sqrt{ {i}^{2} \times 25} \)
\(\qquad \sf \dashrightarrow \: 5i\)
so, correct choice is D
\( \sqrt{ - 25} \)
To find:The equivalent value from the given options.
Solution:\( \sqrt{ - 25} \)
\( = \sqrt{ - 1\times 25} \)
\( = \sqrt{ {i}^{2} \times 25 } \)
\( = 5i\)
Therefore, the correct answer is option D
An observer standing beside a one-lane road counted in 5 minutes 20 cars traveling at 30 mph, 30 cars traveling at 50 mph and 10 cars traveling at 60 mph. (a) What is the space and time-mean speeds of the observed cars? [12 points] (b) What is the average headway of the cars? [3 points]
Answers
(a) An observer standing beside a one-lane road counted in 5 minutes 20 cars traveling at 30 mph, 30 cars traveling at 50 mph and 10 cars traveling at 60 mph. The time-mean speed of the observed cars is 900 mph.
(b) The average headway of the cars is 5.08 minutes (approximately).
(a) To calculate the space and time-mean speeds of the observed cars, we need to consider the total distance traveled and the total time taken by the cars.
Given data:
Number of cars traveling at 30 mph = 20
Number of cars traveling at 50 mph = 30
Number of cars traveling at 60 mph = 10
To find the space-mean speed, we calculate the weighted average of the speeds based on the number of cars at each speed:
Space-mean speed = [(20 cars * 30 mph) + (30 cars * 50 mph) + (10 cars * 60 mph)] / (20 + 30 + 10)
= (600 + 1500 + 600) / 60
= 2700 / 60
= 45 mph
The space-mean speed of the observed cars is 45 mph.
To find the time-mean speed, we calculate the total distance traveled and divide it by the total time taken:
Total distance traveled = (20 cars * 30 mph * 5/60 hours) + (30 cars * 50 mph * 5/60 hours) + (10 cars * 60 mph * 5/60 hours)
= (25 miles + 41.67 miles + 8.33 miles)
= 75 miles
Total time taken = 5 minutes = 5/60 hours
Time-mean speed = Total distance traveled / Total time taken
= 75 miles / (5/60) hours
= 75 miles * (60/5)
= 900 mph
(b) Average headway is the average time interval between successive cars passing a given point.
To find the average headway, we need to calculate the total time taken by all the cars and divide it by the total number of intervals:
Total time taken by all the cars = (20 cars + 30 cars + 10 cars) * 5 minutes
= 60 cars * 5 minutes
= 300 minutes
Total number of intervals = 60 cars - 1 (as there is no interval after the last car)
Average headway = Total time taken by all the cars / Total number of intervals
= 300 minutes / 59 intervals
For more such information on: time-mean speed
https://brainly.com/question/14774965
#SPJ8
The sum of two numbers is equal to 63, and their difference is equal to 12. Find the numbers
Answers
Answer:
25.5 and 37.5
Step-by-step explanation:
x+y=63
x-y = 12 then x = 12 + y sub this into the first equation
(12+y) + y = 63
12 + 2y = 63
2y = 51
y = 25.5 then x = 37.5
Find the volume of the rectangular prism. O 4 m3 O 7 m3 O 28 m3 O 8 m3

Answers
ANSWER:
The volume of the rectangular prism is 4 m^3
STEP-BY-STEP EXPLANATION:
We have that the volume of a rectangular prism is given by the following formula
\(\begin{gathered} V=l\cdot w\cdot h \\ \text{where l is the length, w is the width and h is the height} \end{gathered}\)replacing:
\(\begin{gathered} V=4\cdot2\cdot1 \\ V=8 \end{gathered}\).
Which of the following shows a graph of the equation above?
Answers
Can you provide more information?
Which expression is equivalent to (7-8) (78)?
А
49-5
B
49-11
C
7-5
D 7-11
Answers
-78
Step-by-step explanation:
(7-8)(78)
(-1)(78)=-78
two more after this one

Answers
The amount of money that Lisa would have after 9 years is equal to $5,183.2.
How to calculate the future value?Mathematically, compound interest can be calculated by using this formula:
A(t) = P(1 + r/n)^{nt}
Where:
A represents the future value.n represents the number of times compounded.P represents the principal.r represents the interest rate.T represents the time measured in years.Substituting the given parameters into the compound interest formula, we have;
Future value, A(t) = 4,000(1 + 0.029/2)^{2 × 9}
Future value, A(t) = 4,000(1 + 0.0145)^{18}
Future value, A(t) = 4,000(1.0145)^{18}
Future value, A(t) = 4,000(1.2957968642629875)
Future value, A(t) = $5,183.2.
Read more on interest rate here: brainly.com/question/26343258
#SPJ1
In the equation 5 + 3x - 7 = 10, what are the like terms?
Answers
Answer:
5 , -7 , 10
Step-by-step explanation:
How do you find the base area of a rectangular prism when given the volume?
Answers
you can use the formula for the volume of a rectangular prism to solve for one of the dimensions of the prism (either the length, width, or height).
What is a rectangular prism?
A rectangular prism is a three-dimensional shape with six rectangular faces. It is also known as a box or a cuboid. A rectangular prism has three dimensions: length, width, and height.
To find the base area of a rectangular prism when given the volume, you can use the formula for the volume of a rectangular prism and the formula for the base area of a pyramid.
The volume of a rectangular prism is given by the formula V = lwh,
where V is the volume, l is the length, w is the width, and h is the height.
The base area of a pyramid is given by the formula B = A/h,
where B is the base area, A is the total surface area of the pyramid, and h is the height of the pyramid.
To learn about rectangular prism, Visit
https://brainly.com/question/24284033
#SPJ4
- 8/3x -3 + 1/3x -1 =5
Answers
Answer:
3 6/7.
Step-by-step explanation:
Answer:
-3 6/7
Step-by-step explanation:
rewrite with 'like' terms next to each other:
-8/3x + 1/3x + (-3) + (-1) = 5
-7/3x + (-4) = 5
-7/3x = 9
multiply each side by -3/7
x = -27 /7 or -3 6/7
If there are 4.8 grams of a radioactive substance present initially and 0.4 grams remain after 13 days, what is the half life?

Answers
Half life of the radioactive substance is 3.6 days
How to calculate the half life of the substanceThe half life of the element is calculated from the formula
N(t) = N'(1/2)^(t/t')
N(t) = quantity of the substance remaining
N' = initial quantity of the substance
t = time elapsed
t' = half life of the substance
0.4 = 4.8 (0.5)^13/t'
0.4 / 4.8 = (0.5)^13/t'
take natural logarithm of both sides
㏑(0.4/4.8) = 13/t' ㏑(0.5)
divide through by natural log of 0.5
-2.4849 / ㏑(0.5) = 13/t'
13/t' = 3.58496
t' = 13 / 3.58496
t' = 3.626 days
Learn more about half life here:
https://brainly.com/question/19318304
#SPJ1
Let's find 2/3 + 1/5
first write the addition with a common denominator.
then add
2/3 + 1/5 =
Answers
Step-by-step explanation:
2/3 + 1/5= 2/15 + 1/15 =3/15 or 1/3
answer: 3/15 or 1/3
Help! Find the domain of the graph

Answers
Answer:
-5 < x < 5
Step-by-step explanation:
-5 < x < 5
Paul received a coupon for 43 percent off one item at a clothing store let b be the original price of the item use the expression b-43 for the new price of the item write an equivalent expression by combining like terms
Answers
The equivalent expression for the new price of the item is 0.57b. With b be the original price of the item.
The original price of the item is represented by "b". Paul received a coupon for "43 percent" off one item at a clothing store. This means that the new price of the item will be the "original price" minus the discount. The discount is calculated by multiplying the original price by the percentage discount.
So, the discount is:
43 percent of b = 0.43 * b
The new price of the item is the original price minus the discount:
b - 0.43 * b = b - 0.43b
This expression can be simplified by combining the like terms. The like terms in this expression are b and -0.43b.
To combine like terms, we add the coefficients of the like terms:
1b + (-0.43)b = 0.57b
So, the equivalent expression for the new price of the item is:
0.57b
This means that the new price of the item is 57% of the original price. Therefore, the equivalent expression for the new price of the item is 0.57b.
Here to learn more about the Equivalent Expression at the link https://brainly.com/question/15775046
#SPJ11
Help please!!!
12x + 6y= 162
2x + 10y= 126
Solve using system of equations. Show all work
Answers
Answer:
(8, 11)
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDASEquality PropertiesAlgebra I
Solving systems of equations using substitution/eliminationStep-by-step explanation:
Step 1: Define systems
12x + 6y = 162
2x + 10y = 126
Step 2: Simplify systems
2x + y = 27
x + 5y = 63
Step 3: Rewrite systems
2x + y = 27
x = 63 - 5y
Step 4: Solve for y
Substitute in x: 2(63 - 5y) + y = 27Distribute 2: 126 - 10y + y = 27Combine like terms: 126 - 9y = 27Isolate y term: -9y = -99Isolate y: y = 11Step 5: Solve for x
Define equation: x + 5y = 63Substitute in y: x + 5(11) = 63Multiply: x + 55 = 63Isolate x: x = 8Answer:
x = 8 and y = 11
Step-by-step explanation:
solve for y
12x + 6y = 162
-12x -12x
6y = 162 - 12x
/6 /6
y = 27 - 2x
substitute
2x + 10(y) = 126
2x + 10(27 - 2x) = 126
2x + 270 - 20x = 126
-18x + 270 = 126
-270 -270
-18x = -144
-18 -18
x = 8
substitute again:
y = 27 - 2(x)
y = 27 - 2(8)
y = 27 - 16
y = 11
8 friends share 1/3 of a bag of chips. If they each get an equal share how much of the bag of chips does each friend get?
Answers
Answer:
0.04166666666
I think, im not sure
Step-by-step explanation:
1/3 divided 8 = 0.417 (rounded)
According to a USA Today "Snapshot," 3% of Americans surveyed lie frequently. You conduct a survey of 500 college students and find that 20 of them lie frequently. Compute the probability that in a random sample of 500 college students, at least 20 lie frequently, assuming the true percentage is 3%. Does this result contradict the USA Today Snapshot? Explain.
Answers
According to the USA Today "Snapshot," 3% of Americans surveyed lie frequently. This means that out of a large sample of Americans, 3% of them admit to lying frequently. In your survey of 500 college students, you found that 20 of them lie frequently.
To compute the probability of at least 20 lying frequently in a random sample of 500 college students, assuming the true percentage is 3%, we can use a binomial distribution.
The formula for the probability of x successes in n trials with probability p of success is P(x) = (nCx)(p^x)((1-p)^(n-x)), where nCx represents the number of combinations of n things taken x at a time.
Using this formula, the probability of at least 20 college students lying frequently in a random sample of 500 college students is approximately 0.00002, or 0.002%. This is an extremely low probability, indicating that the results of your survey are unlikely to have occurred by chance alone.
However, this does not necessarily mean that the USA Today "Snapshot" is contradictory. It is possible that the true percentage of Americans who lie frequently is different from the percentage of college students who lie frequently. Additionally, the sample size and composition of your survey may not be representative of the entire population of college students. Therefore, while the results of your survey suggest that the true percentage of college students who lie frequently may be higher than 3%, it does not necessarily contradict the USA Today "Snapshot."
According to a USA Today "Snapshot," 3% of Americans surveyed lie frequently. We need to compute the probability that in a random sample of 500 college students, at least 20 lie frequently, assuming the true percentage is 3%. To do this, we can use the binomial probability formula:
P(x >= 20) = 1 - P(x <= 19)
Here, n = 500 (sample size), p = 0.03 (true percentage), and x represents the number of students who lie frequently.
Step 1:
Calculate the cumulative probability P(x <= 19):
We can use a cumulative binomial probability table or a calculator with a binomial cumulative distribution function (CDF). Using the CDF, we get:
P(x <= 19) = binomcdf(500, 0.03, 19) ≈ 0.964
Step 2:
Calculate the probability P(x >= 20):
P(x >= 20) = 1 - P(x <= 19) = 1 - 0.964 = 0.036
The probability that at least 20 out of 500 college students lie frequently is 0.036 or 3.6%. This result is slightly higher than the USA Today Snapshot's 3% figure.
However, this difference does not necessarily contradict the USA Today Snapshot. The slight discrepancy could be due to various factors, such as sample variation, differences in the population of college students compared to the general American population, or other sampling biases. The probability we calculated (3.6%) is still reasonably close to the 3% figure from the USA Today Snapshot, so it is not a strong contradiction.
Learn more about difference at : brainly.com/question/2432925
#SPJ11
3.53 divided by 51
24.2 divided by 42
9.13 divided by 23
79.2 divided by 39
Answers
Answer:
1. 0.0692156863
2. 0.5761904762
3. 0.3969565217
4. 2.030769231
Step-by-step explanation:
In trapezoid ABCD(AB ∥CD), point M∈AD, so that AM:MD=3:5. Line l ∥ AB and passes through point M to intersect diagonal AC and leg BC at points P and N ,respectively. Find AC:PC.
there are no pictures. Will give brainlest.
Answers
Step by step explanation