an electrician charges a flat service fee to accept a job and an additional hourly rate to complete the job. the amount an electrician charges per job can be represented by the function e(x)
Answers
The correct interpretation is For every hour the electrician works, her pay will increase by $32. The correct option is A.
What is the equation of a line?
A line is a flat, one-dimensional structure that can go on forever in both directions and is straight. A line's equation is given by, y =mx + c
where,
x is the coordinate of the x-axis,
y is the coordinate of the y-axis,
m is the slope of the line, and
c is the y-intercept.
Given that an electrician bills a one-time flat service cost for accepting a task and an additional hourly rate for finishing it. The function E(x) = 135 + 32x, where x is the number of hours she works on the task and 135 is her flat service fee, can be used to express the amount an electrician bills per job.
The slope interpretation for the presented problem is that the electrician's income will rise by $32 for every hour that she works.
Therefore, the accurate interpretation is that the electrician's pay will rise by $32 for every hour that she works.
for detail question see reference attachment
To learn more about Equation line visit:
brainly.com/question/21511618
#SPJ4

Related Questions
Jacee has had her eye on a dress. It originally cost $65. It is on sale for 33% off. How much will the dress cost before taxes?t?
$21.45
$33
$43.55
$86.45
Answers
Answer: 21.45$
Step-by-step explanation: I can’t explain how i got it but i hope this helped!
Answer:
$43.55
Step-by-step explanation:
I took 65 and found 33% by making 33% .33 and did 65*33, then subtracted what I got from the total of 65, 65-21.45 which is $43.55.
express x^2-8x+20 in the form (x-a)^2+a where a is an integer
Answers
Answer:
(x-4)²+4
Step-by-step explanation:
Answer:
\((x-4)^2+4\)
Step-by-step explanation:
\(x^2 - 8x + 20\\**********************************\\\frac{8}{2} =( 4 )^2 = 16 \\\\20 - 16 = 4\\**********************************\\x^2 - 8x + 16 + 4\\(x-4)^2+4\)
36/38 in its simplest form??

Answers
Answer:
18 / 19
Step-by-step explanation:
Divide it by 2
A 5. 1m long ladder is leaning against a wall the wall stands perpendicular to the ground the base of the adder is 1. 8m from the wall. Work out the size of the acute angle that the ladder makes with the ground give your answers in degrees to 1dp
Answers
The acute angle that the ladder makes with the ground is 70.94°.
To work out the size of the acute angle that the ladder makes with the ground, we need to use trigonometry. Let's call the angle we're trying to find "theta" (θ). We know that the ladder is the hypotenuse of a right-angled triangle, with the wall being one side and the ground being the other. Using the Pythagorean theorem, we can work out the length of the ladder's side of the triangle:
a² + b² = c²
where a = 1.8m (the distance from the wall to the base of the ladder), b =? (the distance from the base of the ladder to the ground), and c = 5.1m (the length of the ladder).
Rearranging this formula, we get:
b² = c² - a²
b² = (5.1)² - (1.8)²
b² = 24.21
b = √24.21
b = 4.92m (to 2 decimal places)
Now that we know the lengths of the sides of the triangle, we can use trigonometry to find the angle θ. Specifically, we can use the tangent function:
tan(θ) = opposite/adjacent
where opposite = b (the distance from the base of the ladder to the ground) and adjacent = a (the distance from the wall to the base of the ladder).
tan(θ) = 4.92/1.8
tan(θ) = 2.7333 (to 4 decimal places)
Now we need to find the inverse tangent (or arctan) of this value to get the angle θ:
θ = arctan(2.7333)
θ = 70.94° (to 1 decimal place)
Therefore, the acute angle that the ladder makes with the ground is 70.94°.
Learn more about trigonometry here:
https://brainly.com/question/12068045
#SPJ11
What is the equation of a parabola that passes through the points (−5, −10), (−3, 2), and (2, −3)?
A. y = −x2 − 2x + 5
B. y = −x2 + 6x − 7
C. y = −189x2 − 289x + 353
D. y = −x2 − 3x + 2
Answers
Answer:
A
Step-by-step explanation:
Using the standard form of the parabola , y = ax² + bx + c ( a ≠ 0 )
Substitute the given points into the equation and solve for a, b, c using simultaneous equations.
(- 5, 10 )
- 10 = a(- 5)² - 5b + c, that is
25a - 5b + c = - 10 → (1)
(- 3, 2 )
2 = a(- 3)² - 3b + c, that is
9a - 3b + c = 2 → (2)
(2, - 3 )
- 3 = a(2)² + 2b + c , that is
4a + 2b + c = - 3 → (3)
Eliminate c from the equations
Subtract (2) from (1) term by term
16a - 2b = - 12 → (4)
Subtract (3) from (2) term by term
5a - 5b = 5 → (5)
Multiply (4) by 5 and (5) by - 2 then add to eliminate b
80a - 10b = - 60 → (6)
- 10a + 10b = - 10 → (7)
Add (6) and (7) term by term
70a = - 70 ( divide both sides by 70 )
a = - 1
Substitute a = - 1 into (4) and evaluate for b
- 16 - 2b = - 12 ( add 16 to both sides )
- 2b = 4 ( divide both sides by - 2 )
b = - 2
Substitute a = - 1, b = - 2 into (3) and evaluate for c
- 4 - 4 + c = - 3
- 8 + c = - 3 ( add 8 to both sides )
c = 5
Thus a = - 1, b = - 2 and c = 5
Substitute these values into the standard parabola, that is
y = - x² - 2x + 5 → A
Here we want to find the equation of the parabola that passes through the points (-5, -10), (-3, 2), and (2, -3).
We will get, by brute force, that the correct option is A:
y = -x^2 - 2x + 5
To find the correct option we can use brute force.
We do know the options, so what we can do is just evaluate the given options in the x-values of the points, and see if we get the same y-value that the point.
We can start with option A:
A: y = -x^2 - 2x + 5
For the first point (-5, -10) we have x = -5, evaluating in this we get:
y = -(-5)^2 - 2*(-5) + 5 = -25 + 10 + 5 = -10
Now let's try with the next point (-3, 2), we have x = -3
y = -(-3)^2 - 2*(-3) + 5 = -9 + 6 + 5 = 2
Now we can try with the last point (2, -3), where x= 2
y = -(2)^2 - 2*2 + 5 = -4 - 4 + 5 = -3
So we got all the correct y-values (the second value for each point) thus we can conclude that this one is the correct option.
The correct option is A: y = -x^2 - 2x + 5
If you want to learn more, you can read:
https://brainly.com/question/21685473
Prove the question
1/(tan 2 theta - tan theta) - 1/(cot 2theta - cot theta) = cot theta

Answers
To prove the equation \(\frac{1}{\tan(2\theta) - \tan(\theta)} - \frac{1}{\cot(2\theta) - \cot(\theta)} = \cot(\theta)\) we'll simplify the left side, this is shown below:
How to solveUsing the trigonometric identities \(\tan(2\theta) = \frac{2\tan(\theta)}{1 - \tan^2(\theta)}\) and \(\cot(\theta) = \frac{1}{\tan(\theta)}\)
We can rewrite the expression as \(\frac{1}{\tan(\theta)(1 - \tan(\theta))} - \frac{\tan(\theta)}{\tan(\theta)(1 - \tan^2(\theta))}\)
Combining the fractions with a common denominator, we obtain \(\frac{1 - \tan(\theta)}{\tan(\theta)(1 - \tan(\theta))}\)
Simplifying further, we cancel out the \((1 - tan(\theta))\) terms, leaving us with \(\frac{1}{\tan(\theta)}\) = \(\cot(\theta)\), which is equivalent to the right side of the equation.
Thus, the equation is proven.
Read more about trigonometric identities here:
https://brainly.com/question/7331447
#SPJ1
one-third of a number is at least 5 units from 31
Answers
Answer:
6
Step-by-step explanation:
5^2+6=31
25+6=31
31=31
proved
One-third of the number is at least 5 units from 31. The number is 78.
What is an expression?Expression in maths is defined as the collection of numbers variables and functions by using signs like addition, subtraction, multiplication, and division.
Numbers (constants), variables, operations, functions, brackets, punctuation, and grouping can all be represented by mathematical symbols, which can also be used to indicate the logical syntax's order of operations and other features.
Given that one-third of a number is at least 5 units from 31. The unknown number is x.
( 1 / 3 )x + 5 = 31
x + 15 = 31 x 3
x + 15 = 93
x = 93 - 15
x = 78
Therefore, one-third of the number is at least 5 units from 31. The number is 78.
To know more about an expression follow
https://brainly.com/question/723406
#SPJ2
I will mark the brainiest!

Answers
Answer:
B: 375 ft^2
Step-by-step explanation:
20 x 15 + 10 x 15/2 = 375
in a scientific research, a statistical test resulted in a -value of 0.026. match each value with the correct decision. (a) do not reject h0 (b) reject h0
Answers
Any p-value less than 0.05 is a cause to reject the null hypothesis.
What is Null Hypothesis?
The statement "The null hypothesis is a claim about population parameter that is assumed to be false until it is declared false" is false. The null hypothesis is denoted by H0 assumes that the claim you are trying to prove did not happen. It is a claim about a population parameter that is assumed to be true until it is declared false.
In this case, 0.015 is the only option for p-value that would lead to a rejection of the null hypothesis (if the level of significance for the test is 0.05).
Any p-value less than 0.05 is a cause to reject the null hypothesis.
To know more about Null Hypothesis visit : brainly.com/question/28920252
#SPJ4
Find the slope between the points (-3, -2) and (5, 4) (type in integer or reduced fraction you found only)
Answers
Answer:
The slope is: \(\frac{3}{4}\)
Step-by-step explanation:
The equation for slope is:
\(m=\frac{y_{2}- y_{1} }{x_{2} -x_{1} }\)
Point 1: -3=\(x_{1}\), -2=\(y_{1}\)
Point 2: 5=\(x_{2}\), 4=\(y_{2}\)
4-(-2)=6
5- (-3)=8
6/8=3/4
Help please...
15 points and brainliest if right

Answers
Answer:
I belive it is the second one
Step-by-step explanation:
Answer:
B. The second box plot
Step-by-step explanation:
Min: 9.1Lower Quartile: 9.2Median: 9.4Upper Quartile: 9.7Max: 9.8In the diagram below of AACD, DB is a median to AC, and AB = DB.
D
A
B
c
If mZDAB = 32°, what is mZBDC?
(1) 320
(3) 58°
(2) 520
(4) 64°

Answers
Answer:
it will be (3)
Step-by-step explanation:
since DB is a median
then DB= half AC , AB=BC
then AB=BD
then the two triangles are isosceles
The required m∠BDC is 32° .
In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, thus bisecting that side. Every triangle has exactly three medians, one from each vertex, and they all intersect each other at the triangle's centroid.
According to the given question ;
DB is a median;
By the symmetry ;
Then DB = half AC ,
= AB = BC
Then= AB = BD
In a triangle, a line that connects one corner (or vertices ) to the middle point of the opposite side is called a median. A property of isosceles triangles, which is simple to prove using triangle congruence, is that in an isosceles triangle the median to the base is perpendicular to the base.
Then the two triangles are isosceles.
Means m∠DAB = m∠BDC = 32°
For the more information about the properties of isosceles triangle click the link given below.
https://brainly.in/question/13106654
What is the circumference of a circle with a diameter of 72 feet? Leave your answer in
terms of pi.
Answers
Answer:
72π feet
Step-by-step explanation:
circumference of circle= 2πr
Diameter= 2(radius)
radius of circle
= 72 ÷2
= 36 ft
Circumference
= 2(π)(36)
= 72π ft
I NEEEED answers WITH 5.3.3 in CONNEXUS FOR MATH PLSSS
A square has a perimeter of 12 units. One vertex is at the point left-parenthesis negative 1 comma 1 right-parenthesis, and another vertex is at the point left-parenthesis 2 comma 4 right-parenthesis. Which of the following points could be another vertex?
A. left-parenthesis 1 comma 2 right-parenthesis
B. left-parenthesis 2 comma 1 right-parenthesis
C. left-parenthesis 1 comma negative 2 right-parenthesis
D. left-parenthesis 2 comma negative 1 right-parenthesis
Answers
Another possible vertex of the square is determined as (2, 1).
option B is the correct answer.
What is the vertex of the square?The vertex of a figure is the point of intersection of two sides of the shape.
The perimeter of the square is given as 12 units, the length of each side of the square is calculated as follows;
P = 12 units
a side length = 12 units / 4 = 3 units
To determine another possible vertex of the square, the length between the points must be equal to 3.
Let's consider point A;
A = (1, 2)
given vertex = (-1, 1)
distance between the points = √ (-1 -1)² + (1 - 2)² = √5
Let's consider point B;
B = (2, 1)
given vertex = (-1, 1)
distance between the points = √ (-1 -2)² + (1 - 1)² = √9 = 3
Thus, point B is another possible vertex of the square.
Learn more about vertex of a square here: https://brainly.com/question/23627218
#SPJ1
a pharmaceutical company wants to conduct a survey of 40 individuals who have high cholesterol. the company has obtained a list from primary care physicians throughout the country of 6800 individuals who are known to have high cholesterol. design a sampling method to obtain the individuals in the sample. be sure to support the choice. question content area bottom part 1 what sampling method(s) is/are valid? select all that apply.
Answers
The valid sampling method(s) for obtaining a sample of individuals with high cholesterol from the list provided are simple random sampling, stratified sampling, and cluster sampling.
- Simple random sampling: This method involves randomly selecting 40 individuals from the list of 6800 individuals.
- Stratified sampling: This method involves dividing the list of 6800 individuals into different strata based on relevant characteristics.
- Cluster sampling: This method involves dividing the list of 6800 individuals into smaller clusters (e.g., primary care physician offices or geographical areas).
This method is useful when it is difficult or costly to reach individuals scattered across a wide area.
Each of these methods has its advantages and disadvantages, so the choice depends on the specific needs and constraints of the pharmaceutical company.
To know more about sampling visit:
brainly.com/question/30269161
#SPJ11
i need help with this i am really bad at math

Answers
Answer:
You subtracted 25 from both sides.
Step-by-step explanation:
To move one part of the equation to the other side, you need to do the opposite. 25 is already negative(or being subtracted) so you need to add it to both sides to cancel it out on the left.
10x=-75+25
10x=-50
then divide both sides by 10
x=-5
Thirty percent of high-school senior boys play in the school band. If a certain high school has 60 senior boys, how many boys play in the school band?
(A) 12
(B) 18
(C) 22
(D) 30
Answers
Find m1 and m2 . Tell which theorem can be used.
m1 =
by the…
m2 =
by the…
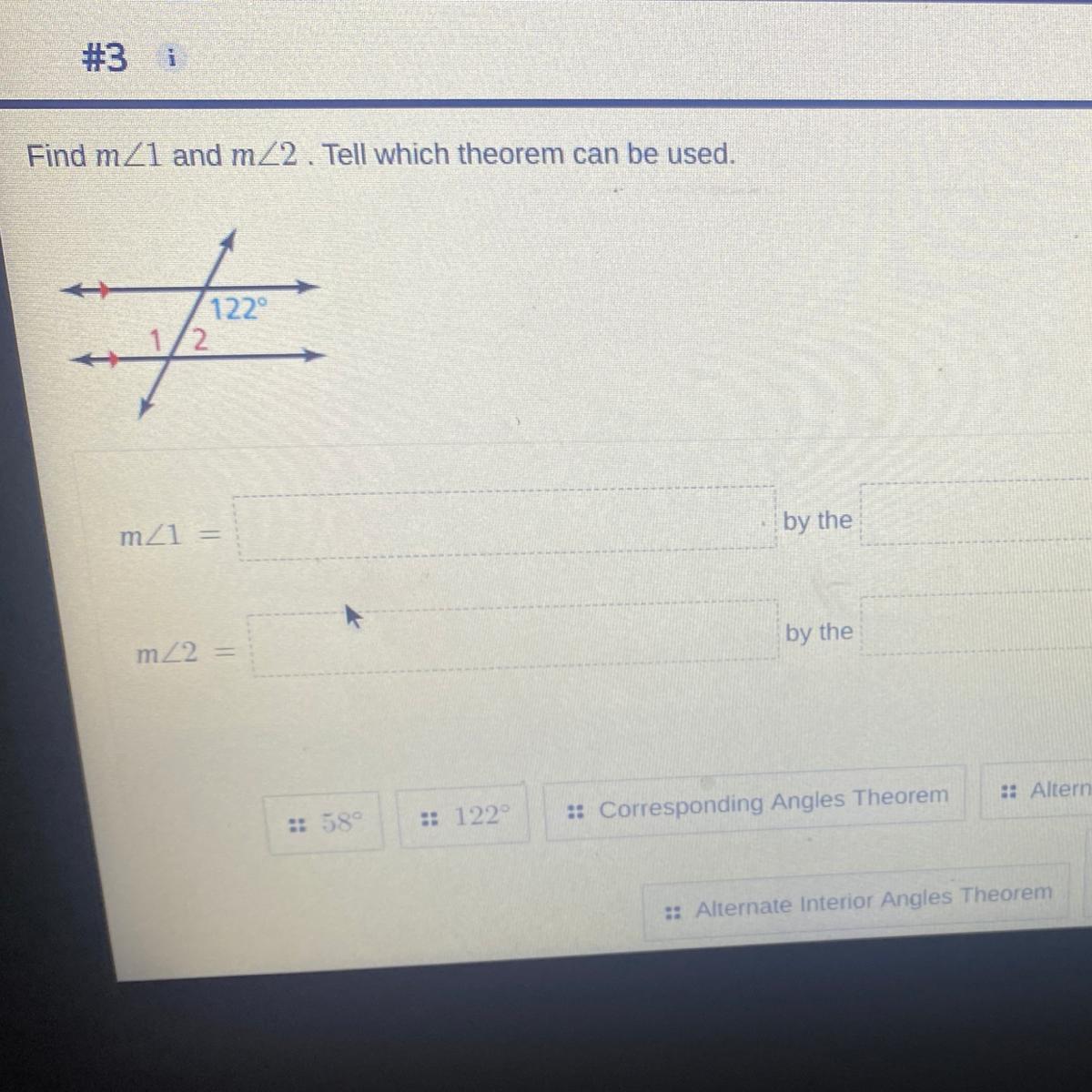
Answers
122° and angle 1 are alternate interior angles and hence they are equal.
m1 = 122°
122° + angle 2 = 180° [sum of co interior angles is 180°]
angle 2 = 180° - 122°
m2 = 58°
A civil servant had a salary of Rs 9600. Tax up to Rs 85000 per year would be exempted. If he paid Rs 4530 as a tax, how much percent of tax was imposed?
Answers
Answer:
4%
Step-by-step explanation:
Yearly salary = 9600 * 12 = Rs. 115200
Tax = Rs . 4530
\(Tax \ percent = \frac{4530}{115200}*100\)
= 3.93 = 4%
A cylinder has a radius of 1.2 meters. Its volume is 48 cubic
meters. Use 3.14 for pi. Find its height to the nearest tenth
of a meter.
Answers
Answer:
10.6m
Step-by-step explanation:
height of cylinder:
h= V/pie r^2
h= 48/3.14x1.2^2
h=48/3.14x1.44
h=48/4.5216
h=10.61meter
round to the nearest tenth
= 10.6m
Please mark as brainliest
Find the minimum radius of convergence of power series solutions about the ordinary point xo = 2. (x^3 - 2x^2 + 3x)y" + x(x-3)^2 y' - (x + 1)y = 0
Answers
On dividing the whole equation by
$a_{n+2}$
and taking the limit as
$n \rightarrow \infty$,
we get:
$$\lim_{n\to\infty} \frac{(n+2)(n+1)a_{n}}{a_{n+2}} = 2$$
This is the ratio test to determine the radius of convergence of the power series. Since the limit is 2, the radius of convergence is 1/2. Therefore, the minimum radius of convergence of power series solutions about the ordinary point xo = 2 is 1/2.
The differential equation can be expressed as
:$(x^3 - 2x^2 + 3x)y"+ x(x-3)^2 y' - (x + 1)y
= 0$
The first step to find the power series solution of the differential equation is to verify that
xo
= 2
is a point of the ordinary differential equation. Since both coefficients in this case are analytic at x
= 2, 2 is an ordinary point.Let
$y
= \sum_{n=0}^{\infty} a_n(x-2)^n$
be the power series solution of the given differential equation. Then
,$y'
= \sum_
{n=1}^{\infty} a_nn(x-2)^{n-1}$and $y''
= \sum_{n
=2}^{\infty} a_nn(n-1)(x-2)^{n-2}$
Substituting these in the differential equation we get
:$(x^3 - 2x^2 + 3x)\sum_{n
=2}^{\infty} a_nn(n-1)(x-2)^{n-2}+ x(x-3)^2 \
sum_{n=1}^{\infty} a_nn(x-2)^{n-1} - (x + 1) \sum_{n=0}^{\infty} a_n(x-2)^n
= 0$$$\sum_{n=0}^{\infty} [a_{n+2}(n+2)(n+1)x^{n+1} -2a_{n+1}(n+2)x^{n+1} + 3a_n x^{n+1}] + \
sum_{n=1}^{\infty} [a_n x^{n+2} - 3a_n x^{n+1} + 2a_n x^n] - \sum_{n=0}^{\infty} [a_n x^{n+1} + a_n x^n]
= 0$$
Comparing the coefficients of
x^n, we have:
$a_{n+2}(n+2)(n+1) - 2a_{n+1}(n+2) + (3-a_n)
= 0$
On dividing the whole equation by
$a_{n+2}$
and taking the limit as
$n \rightarrow \infty$, we get
:$$\lim_{n\to\infty} \frac{(n+2)(n+1)a_{n}}{a_{n+2}}
= 2$$
This is the ratio test to determine the radius of convergence of the power series. Since the limit is 2, the radius of convergence is 1/2. Therefore, the minimum radius of convergence of power series solutions about the ordinary point xo
= 2 is 1/2.
To know more about convergence visit:
https://brainly.com/question/29258536
#SPJ11
9 + 12 - 219 - 22) > 0
Answers
Answer:
-232
Step-by-step explanation:
9+12=21
21-219= -198
-198-22= -232
a right triangle is shown, m
Answers
Answer:
WHAT
Step-by-step explanation:
Answer: 7\(\sqrt{2}\)
Step-by-step explanation: Khan Academy
Can some one please help me answer this question, thank you for your time in advance

Answers
Answer:
Step-by-step explanation:
B
Find the sampled time domain from the following functions (a) \( F(z)=1+3 z^{-1}+4 z^{-2} \)
Answers
In the given question function given is \(F(z)=1+3z^{-1} +4z^{-2}\) and by performing Z transform we get sampled time domain as f(n)=1 for all values of n
In the given question function given is \(F(z)=1+3z^{-1} +4z^{-2}\) and by performing Z transform we get sampled time domain as f(n)=1 for all values of n
In the given question function given is \(F(z)=1+3z^{-1} +4z^{-2}\) and by performing Z transform we get sampled time domain as f(n)=1 for all values of n we need to perform the inverse Z-transform. The inverse Z-transform converts a function in the Z-domain back into the time domain.
The general form of the inverse Z-transform is given by:
f(n)= \(\frac{1}{2\pi j}\) ∮ \(_{C}\) \(F(z)z^{n-1} dz\)
where
F(z) is the function in the Z-domain, f(n) is the corresponding time-domain sequence, j is the imaginary unit, and ∮\(_{c}\)
represents integration around a closed path in the Z-plane.
In this case, the function F(z) is a rational function, and we can find its inverse Z -transform using partial fraction decomposition. Let's find the inverse Z-transform step by step:
Step 1: Express F(z) in partial fraction form.
\(F(z)=\frac{1}{z^2} + \frac{3}{z} +4\)
Step 2: Find the roots of the denominator The roots of \(z^{2} =0\) and
z=0 (a double pole at the origin).
Step 3: Perform partial fraction decomposition.
We can write \(F(z)=\frac{A}{z} +\frac{B}{z^2} \)
Multiplying through by \(z^{2}\) to clear the fractions we get,\(1+3z^{-1} +4z^{-2} = A+Bz^{-1}\) Comparing coefficients, we get:
A=1
B=4
Step4: Apply the inverse Z transform for each term
Inverse Z transform for A/z is \(a^{n}\), where a is the root of corresponding term in the denominator. In this case a=0, so the inverse Z transform of A/z=1
The inverse Z transform of \(\frac{B}{z^2}\) is n.\(a^{n}\), where a is the root of the corresponding term in denominator. In this case a=0. So the inverse Z transform of \(\frac{B}{z^2}\) is n.\(a^{n}\)=0
therefore the time domain of function f(z) is
f(n)=1+0=1
So the sampled time domain representation of the function F(z)=\(1+3z^{-1} +4z^{-2}\) is f(n)=1 for all the values of n
Learn about rational function here: https://brainly.com/question/27914791
#SPJ11
Consider the following set of equations:
Equation R: −3y = −3x − 9
Equation S: y = x + 3
Which of the following best describes the solution to the given set of equations?
a
No solution
b
One solution
c
Infinite solutions
d
Two solutions
Answers
The solution to the given set of equations is Infinite solutions.
We have the equation
R: -3y = -3x -9
S: y = x + 3
Now, solving the equation R and S as
-3y = -3x - 9
3y = 3x + 9
_________
0 = 0 + 0
0 = 0
Also, -3/1 = 3/(-1) = 9/(-3)
-3/1 = -3/1 = -3/1
Thus, the equation have Infinite many solutions.
Learn more about Equation here:
https://brainly.com/question/29657983
#SPJ1
Negative four and one-fifth minus negative thirteen and one-tenth
Answers
Answer:
8 nine tenths
Step-by-step explanation:
(-21/5) - (-131/10)
(-42/10)-(-131/10)
131-42=89
89/10
8 and nine- tenths or 8 9 divided by 10
The number of international tourist arrivals in Russia in 2012 was 13.5% greater than in 2011. The number of international tourist arrivals in Russia was k million more in 2012 than in 2011. What is the value of k to the nearest integer
Answers
The value of k to the nearest integer is 21
Let the number of international tourist arrivals in Russia in 2011 be kIf the number of international tourist arrivals in Russia in 2012 was 13.5% greater than in 2011 will be expressed as:
k = 24.7 - (13% of 24.7)
k = 24.7 - (0.135 * 24.7)
k = 24.7 - 3.3345
k = 21.3655
Hence the value of k to the nearest integer is 21
Learn more on decrement here: https://brainly.com/question/24304697

What is an equivalent expression for −12(8a − 7b) + 8(4x + 3y)?
−96a + 84b + 32x + 24y
−96a − 84b + 32x − 24y
−96a − 7b + 32x + 3y
−96a + 7b + 32x + 3y
Answers
The equivalent expression for −12(8a − 7b) + 8(4x + 3y) is represented as - 96a + 84b + 32x + 24y
How to solve equivalent expression?Two algebraic expressions are equivalent, then the two expressions have the same value when we plug in the same value(s) for the variable(s).
Therefore, the equivalent expression of −12(8a − 7b) + 8(4x + 3y) can be solved as follows:
−12(8a − 7b) + 8(4x + 3y)
open the bracket
−12(8a − 7b) + 8(4x + 3y)
- 96a + 84b + 32x + 24y
Therefore, the equivalent expression of −12(8a − 7b) + 8(4x + 3y) is - 96a + 84b + 32x + 24y
learn more on equivalent expression here: https://brainly.com/question/10212750
#SPJ1
!!PLEASE HELP ME I'M BEGGING YOU!!
what are 5 solution to the linear equation x - 3 / 2 Y = -2?
Answers
Answer:
There are three major forms of linear equations: point-slope form, standard form, and slope-intercept form. We review all three in this article. There are three main forms of linear equations.
Step-by-step explanation: