An electric car battery, when fully charged, can travel 260 miles. The car uses 232 miles of charge on a drive.
Enter the percentage of miles the car has left in battery charge?

Answers
The percentage of miles the car has left in battery charge is 10.77%
Total distance traveled when fully charged = 260 miles
The total charged used by the car = 232 miles of charges
The remaining charges left in the car battery = Total distance traveled when fully charged - The total charged used by the car
Here we have to use the subtraction
Substitute the values in the equation
= 260 - 232
= 28 miles of charges
The percentage of miles the car has left in battery charge = (28/260) × 100
= 10.77%
Therefore, 10.77% miles of charge left in the battery
Learn more about percentage here
brainly.com/question/17151247
#SPJ4
Related Questions
I need help with these questions. Ignore my failed attempts



Answers
The values of all 9 angles shown were found using the property of a kite they are:
m∠1=55°
m∠2=35°
m∠3=35°
m∠4=90°
m∠5=55°
m∠6=67°
m∠7=67°
m∠8=23°
m∠9=23°
What is an angle ?
In Kite figure, it is given that:
∠2+∠3 = 70°
Since they are equal so ∠2=∠3=35
∠8+∠9 = 46°
Since they are equal so ∠8=∠9=23°
∠5 = 180-∠3-∠4 = 180-35-90=55°
Similarly, ∠1 = 55°
∠6+∠7 = 180-∠8-∠9 = 180-46 = 134°
Since they are equal
∠6=∠7 = 67°
Therefore, all 9 angles were calculated using property of a kite.
m∠1=55°
m∠2=35°
m∠3=35°
m∠4=90°
m∠5=55°
m∠6=67°
m∠7=67°
m∠8=23°
m∠9=23°
In mathematics, an angle is a geometric figure formed by two rays or line segments that share a common endpoint, called the vertex. The rays or line segments are called the sides or legs of the angle, and the distance between the sides at the vertex is called the angle's measure.
Angles are typically measured in degrees or radians, and they can be classified by their measures as acute (less than 90 degrees), right (exactly 90 degrees), obtuse (greater than 90 degrees and less than 180 degrees), straight (exactly 180 degrees), reflex (greater than 180 degrees and less than 360 degrees), or full (exactly 360 degrees).
Kites have several properties related to their angles, including:
Two pairs of opposite angles in a kite are congruent. That is, the angles formed between the pairs of congruent sides are equal.
One diagonal of a kite bisects the other diagonal. This means that the diagonal that connects the non-congruent vertices of the kite divides the other diagonal into two equal segments.
The sum of the measures of the two non-congruent angles in a kite is 180 degrees. This is because the kite can be divided into two congruent triangles by drawing the diagonal that bisects the other diagonal, and the sum of the angles in a triangle is always 180 degrees.
To get more about angle refer to:
https://brainly.com/question/25716982
#SPJ1
Apply the distributive property to factor out the greatest common factor.
24+32p= _____
Answers
Answer:
8(3+4p)
Step-by-step explanation:
8 goes into 24 and 32, so it can be factored out:
\(24+32p=8(3+4p)\)
Answer:
8(3 + 4p)
Step-by-step explanation:
Factor 24 + 32p
First, factor out the GCF. In this case, the GCF is 8, and we have
8(3 + 4p)
We can't factor anymore so the answer is 8(3 + 4p)
Rewrite as a simplified fraction

Answers
The base of an aquarium with given volume v is made of slate and the sides are made of glass. If slate costs three times as much (per unit area) as glass, find the dimensions of the aquarium that minimize the cost of the materials. (let x, y, and z be the dimensions of the aquarium. Enter your answer in terms of v. ).
Answers
The dimensions of the aquarium that minimize the cost of the materials are x = y = ∛-(2V/3) and z = ∛(3V/4).
To find the dimensions of the aquarium that minimize the cost of the materials, we need to find an equation that expresses the total cost of the materials in terms of the dimensions. Let's assume that the height of the aquarium is z, and the base has dimensions x and y.
Since the base is made of slate and the sides are made of glass, the cost C can be expressed as:
C = 3A₁ + A₂
where A₁ is the area of the base covered by slate, A₂ is the area of the sides covered by glass, and the factor of 3 in front of A₁ reflects the fact that slate costs three times as much as glass per unit area.
The volume V of the aquarium is given as V = xyz, so we can express one of the dimensions in terms of the other two, say z = V/(xy). Substituting this expression into the equation for C and simplifying, we get:
C = 3xy + 2xz + 2yz
To minimize C, we need to take the partial derivatives of C with respect to x and y, set them equal to zero, and solve for x and y. Doing so, we get:
∂C/∂x = 3y + 2z = 0
∂C/∂y = 3x + 2z = 0
Solving these equations for x and y in terms of z, we get:
x = -(2/3)z
y = -(2/3)z
Substituting these expressions into the equation for z in terms of V, we get:
z = V/((2/3)z * (2/3)z)
Simplifying this expression, we get:
z = ∛(3V/4)
Substituting this value of z into the expressions for x and y, we get:
x =∛ -(2/3)(3V/4) = ∛-(2V/3)
y = ∛-(2/3)(3V/4) = ∛-(2V/3)
To learn more about dimensions click on,
https://brainly.com/question/14827794
#SPJ4
The account balance on April 1st is $50.51. On April 15th a payment of $15.00 is made. On April 25th a purchase of $19.27 is made. The annual rate is 18%. What is the unpaid balance? What is the finance charge using the unpaid balance method? What is the new balance? Unpaid balance = $ Finance charge = $ New balance = $
describe me in 3 words ;-;
Answers
The new balance is the sum of the unpaid balance, the finance charge, and any new purchases or fees:
New balance = Unpaid balance + Finance charge + Purchase
= $35.51 + $0.84 + $19.27
= $55.62.
We must first identify the balance remaining after the payment and purchase in order to calculate the outstanding balance:
Balance after payment = $50.51 - $15.00 = $35.51
Amount remaining after payment: $35.51 + $19.27 = $54.78
The balance remaining after the payment is made, which comes to $35.51, is the unpaid balance.
We must first determine the average daily balance before we can calculate the finance charge using the unpaid balance technique. Finding the daily balance and dividing the total by the number of days in the billing cycle will allow us to achieve this:
$50.51 times 14 days in April equals $707.
14 April 15–24: $35.51 multiplied by 10 days equals $355.
10 April 25–30: $54.78 multiplied by six days is $328.68
Balance total: $707.14 plus $355.10 plus $328.68 ($1,390.92)
Average daily balance: $1,390.92 divided by 30 equals $46.36.
Hence, the finance charge can be determined as follows:
Finance fee equals $46.36 * (0.18 / 365) * 30 = $0.84. Finance charge formula: Average daily balance * Daily periodic rate * Number of days in billing cycle
The total of the unpaid debt, the finance charge, and any additional purchases or fees is the new balance:
Purchase + Finance fee + New balance = $35.51 + $0.84 + $19.27 = $55.62.
To Know more about Unpaid Balance visit:
https://brainly.com/question/3238364
#SPJ1
Answer:
The account balance on April 1st is $50.51. On April 15th a payment of $15.00 is made. On April 25th a purchase of $19.27 is made. The annual rate is 18%. What is the unpaid balance? What is the finance charge using the unpaid balance method? What is the new balance? Unpaid balance = $ Finance charge = $ New balance = $
Step-by-step explanation:
To calculate the unpaid balance, we first need to calculate the balance after the payment and the balance after the purchase:
Balance after payment on April 15th: $50.51 - $15.00 = $35.51
Balance after purchase on April 25th: $35.51 + $19.27 = $54.78
Next, we need to calculate the average daily balance for the billing period. The billing period runs from April 1st to April 30th, which is 30 days. We can split this into two parts:
April 1st to April 15th (15 days)
April 16th to April 30th (15 days)
For the first part of the billing period, the balance is $50.51 for 15 days. For the second part of the billing period, the balance is $54.78 for 15 days. The average daily balance is therefore:
($50.51 x 15 + $54.78 x 15) / 30 = $52.64
The unpaid balance is the average daily balance minus the payment, so:
$52.64 - $15.00 = $37.64
The finance charge using the unpaid balance method is the unpaid balance multiplied by the daily periodic rate and the number of days in the billing cycle. The daily periodic rate is the annual rate divided by 365 days, so:
Daily periodic rate = 0.18 / 365 = 0.000493
Finance charge = $37.64 x 0.000493 x 30 = $0.56
The new balance is the previous balance (after the purchase) plus the finance charge, so:
New balance = $54.78 + $0.56 = $55.34
Therefore, the unpaid balance is $37.64, the finance charge is $0.56, and the new balance is $55.34.
Study Island Math Help Worth 40 PTS
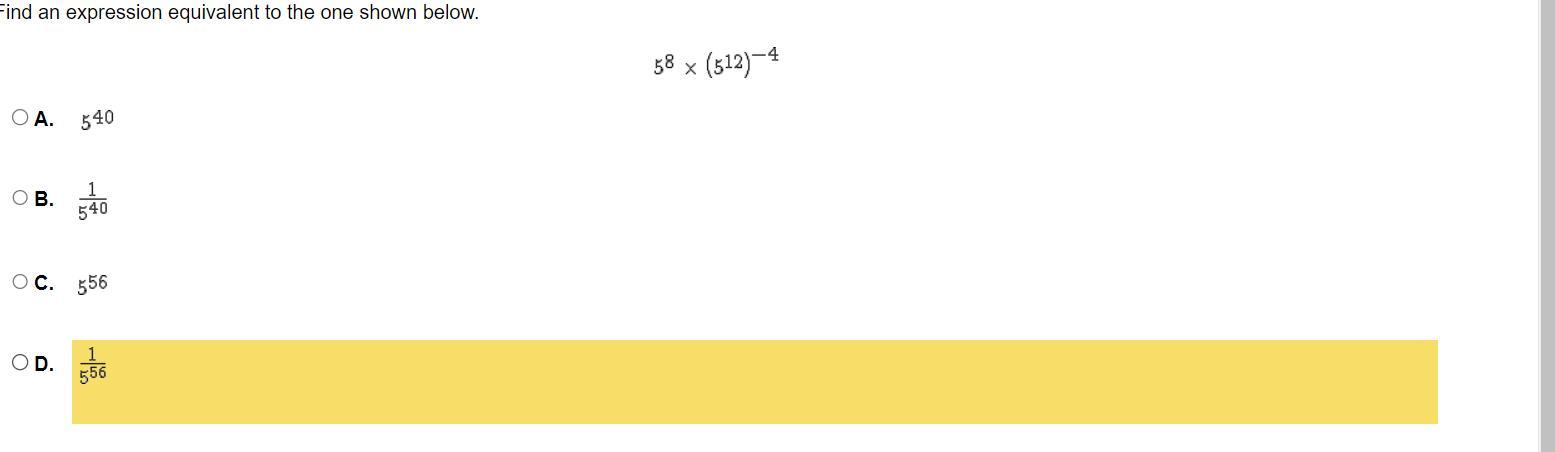
Answers
Answer:
B
Step-by-step explanation:
using the rules of exponents
• \(a^{m}\) × \(a^{n}\) = \(a^{(m+n)}\)
• \(a^{-m}\) = \(\frac{1}{a^{m} }\)
• \((a^m)^{n}\) = \(a^{mn}\)
given
\(5^{8}\) × \((5^{12}) ^{-4}\)
= \(5^{8}\) × \(5^{(12(-4))}\)
= \(5^{8}\) × \(5^{-48}\)
= \(5^{(8-48)}\)
= \(5^{-40}\)
= \(\frac{1}{5^{40} }\)
Dewan’s bank account balance is -$16.75. He deposits checks totaling $23.59. What is his new balance? -$1.08
Answers
Answer:
$6.84
Step-by-step explanation:
This is quite a simple question, simply add the new deposited amount into the original balance to get your answer.
Original balance: -$16.75Deposit: $23.59New balance: -$16.75 + $23.59 = $6.84Use the definition to calculate the derivative of the following function. Then find the values of the derivative as specified.

Answers
Answer:
Refer to the step-by-step explanation, please follow along very carefully. Answers are encased in two boxes.
Step-by-step explanation:
Given the following function, find it's derivative using the definition of derivatives. Evaluate the function when θ=1, 11, and 3/11
\(p(\theta)=\sqrt{11\theta}\)
\(\hrulefill\)
The definition of derivatives states that the derivative of a function at a specific point measures the rate of change of the function at that point. It is defined as the limit of the difference quotient as the change in the input variable approaches zero.
\(f'(x) = \lim_{{h \to 0}} \dfrac{{f(x+h) - f(x)}}{{h}}\)\(\hrulefill\)
To apply the definition of derivatives to this problem, follow these step-by-step instructions:
Step 1: Identify the function: Determine the function for which you want to find the derivative. In out case the function is denoted as p(θ).
\(p(\theta)=\sqrt{11\theta}\)
Step 2: Write the difference quotient: Using the definition of derivatives, write down the difference quotient. The general form of the difference quotient is (f(x+h) - f(x))/h, where "x" is the point at which you want to find the derivative, and "h" represents a small change in the input variable. In our case:
\(p'(\theta) = \lim_{{h \to 0}} \dfrac{{p(\theta+h) - p(\theta)}}{{h}}\\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11(\theta + h)} - \sqrt{11\theta} }{h}\)
Step 3: Take the limit:
We need to rationalize the numerator. Rewriting using radical rules.
\(p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11(\theta + h)} - \sqrt{11\theta} }{h} \\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11\theta + 11h} - \sqrt{11\theta} }{h}\\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11}\sqrt{\theta+h} - \sqrt{11}\sqrt{\theta} }{h}\)
Now multiply by the conjugate.
\(p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11}\sqrt{\theta+h} - \sqrt{11}\sqrt{\theta} }{h} \cdot \dfrac{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} }{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} } \\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{(\sqrt{11}\sqrt{\theta+h} - \sqrt{11}\sqrt{\theta} )(\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} )}{h(\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} )} \\\\\\\)
\(\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{11h}{h(\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} )}\\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{11}{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} }\)
Step 4: Simplify the expression: Evaluate the limit by substituting the value of h=0 into the difference quotient. Simplify the expression as much as possible.
\(p'(\theta)= \lim_{h \to 0} \dfrac{11}{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{\sqrt{11}\sqrt{\theta+(0)} + \sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{\sqrt{11}\sqrt{\theta} + \sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{2\sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{2\sqrt{11\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{2\sqrt{11\theta} }\)
\(\therefore \boxed{\boxed{p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta} }}}\)
Thus, we have found the derivative on the function using the definition.
It's important to note that in practice, finding derivatives using the definition can be a tedious process, especially for more complex functions. However, the definition lays the foundation for understanding the concept of derivatives and its applications. In practice, there are various rules and techniques, such as the power rule, product rule, and chain rule, that can be applied to find derivatives more efficiently.\(\hrulefill\)
Now evaluating the function at the given points.
\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}; \ p'(1)=??, \ p'(11)=??, \ p'(\frac{3}{11} )=??\)
When θ=1:
\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}\\\\\\\Longrightarrow p'(1)= \dfrac{\sqrt{11} }{2\sqrt{1}}\\\\\\\therefore \boxed{\boxed{p'(1)= \dfrac{\sqrt{11} }{2}}}\)
When θ=11:
\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}\\\\\\\Longrightarrow p'(11)= \dfrac{\sqrt{11} }{2\sqrt{11}}\\\\\\\therefore \boxed{\boxed{p'(11)= \dfrac{1}{2}}}\)
When θ=3/11:
\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}\\\\\\\Longrightarrow p'(\frac{3}{11} )= \dfrac{\sqrt{11} }{2\sqrt{\frac{3}{11} }}\\\\\\\therefore \boxed{\boxed{p'(\frac{3}{11} )= \dfrac{11\sqrt{3} }{6}}}\)
Thus, all parts are solved.
HOW IS THE ANSWER 98 PLS HELP ASAP

Answers
Answer:
The answer is 98, here's how:
Step-by-step explanation:
Lets solve the numerator of the fraction first:
-[5.8 - 3(3.2)] =
-[5.8 - 9.6] =
-[-3.8] = 3.8 (Watch out for the double negative)
Now lets solve for the denominator :
(-0.2)² =
(-0.2)(-0.2) = 0.04
Lets simplify the fraction:
\(\frac{3.8}{0.04} = 95\\\)
Let's add the 3 to 95:
95 + 3 = 98
-Chetan K
Step-by-step explanation:
\( \frac{ -[5.8 - 3(3.2)] }{{( - 0.2)}^{2} } + 3\)
\(\frac{ -[5.8 -9.6] }{0.04 } + 3\)
\(\frac{ -( - 3.8)}{0.04} + 3\)
\(\frac{3.8}{0.04} + 3\)
\( = 95 + 3\)
\( = 98\)
50% of 200: fifty percent of two-hundred is?
Answers
Answer:
100
Step-by-step explanation:
Answer:
its 100
Step-by-step explanation:
23+4⋅2−7
the 23 is 2 to the third power.
Answers
Answer:
12618
Step-by-step explanation:
23x23x23=12617
4•2=8
12617+8=12625
12625-7=12618
Answer: 9
Step-by-step explanation:
The correct answer to \(2^{3} + 4\) ⋅ \(2 - 7 = 9\)
I hope that helps :)
In developing an interval estimate of the population mean, if the population standard deviation is unknown _____.
Answers
Answer:
the sample standard deviation and t distribution can be used
Step-by-step explanation:
Suppose you select 4 skittles at random from the bowl. What is the proba- bility exactly 1 of those skittles is green
Answers
Answer:
1/4
Step-by-step explanation:
4 skittles and one being green
Answer:
4/5
Step-by-step explanation:
According to the Wrigley's Consumer Care Department, the fruit candies are produced in equal proportions— 20% of each of the five colors (green, red, orange, yellow, and purple). However, although these candies are made in equal proportions, the individual Skittles bags are filled by weight and by machines but on average I'd say 4/5 chance its a green.
ratios equilvalent to 3:11
Answers
9:33
12:44
15:55
18:66
Heeeelp please, Can be zero or not?
with all steps and explanay.

Answers
The value of integral is 3.
Let's evaluate the integral over the positive half of the interval:
∫[0 to π] (cos(x) / √(4 + 3sin(x))) dx
Let u = 4 + 3sin(x), then du = 3cos(x) dx.
Substituting these expressions into the integral, we have:
∫[0 to π] (cos(x) / sqrt(4 + 3sin(x))) dx = ∫[0 to π] (1 / (3√u)) du
Using the power rule of integration, the integral becomes:
∫[0 to π] (1 / (3√u)) du = (2/3) . 2√u ∣[0 to π]
Evaluating the definite integral at the limits of integration:
(2/3)2√u ∣[0 to π] = (2/3) 2(√(4 + 3sin(π)) - √(4 + 3sin(0)))
(2/3) x 2(√(4) - √(4)) = (2/3) x 2(2 - 2) = (2/3) x 2(0) = 0
So, the value of integral is
= 3-0
= 3
Learn more about Definite integral here:
https://brainly.com/question/30760284
#SPJ1
Answer:
\(3-\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3 \sin x}}\; \text{d}x\approx 0.806\; \sf (3\;d.p.)\)
Step-by-step explanation:
First, compute the indefinite integral:
\(\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x\)
To evaluate the indefinite integral, use the method of substitution.
\(\textsf{Let} \;\;u = 4 + 3 \sin x\)
Find du/dx and rewrite it so that dx is on its own:
\(\dfrac{\text{d}u}{\text{d}x}=3 \cos x \implies \text{d}x=\dfrac{1}{3 \cos x}\; \text{d}u\)
Rewrite the original integral in terms of u and du, and evaluate:
\(\begin{aligned}\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=\int \dfrac{\cos x}{\sqrt{u}}\cdot \dfrac{1}{3 \cos x}\; \text{d}u\\\\&=\int \dfrac{1}{3\sqrt{u}}\; \text{d}u\\\\&=\int\dfrac{1}{3}u^{-\frac{1}{2}}\; \text{d}u\\\\&=\dfrac{1}{-\frac{1}{2}+1} \cdot \dfrac{1}{3}u^{-\frac{1}{2}+1}+C\\\\&=\dfrac{2}{3}\sqrt{u}+C\end{aligned}\)
Substitute back u = 4 + 3 sin x:
\(= \dfrac{2}{3}\sqrt{4+3\sin x}+C\)
Therefore:
\(\displaystyle \int \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x= \dfrac{2}{3}\sqrt{4+3\sin x}+C\)
To evaluate the definite integral, we must first determine any intervals within the given interval -π ≤ x ≤ π where the curve lies below the x-axis. This is because when we integrate a function that lies below the x-axis, it will give a negative area value.
Find the x-intercepts by setting the function to zero and solving for x in the given interval -π ≤ x ≤ π.
\(\begin{aligned}\dfrac{\cos x}{\sqrt{4+3\sin x}}&=0\\\\\cos x&=0\\\\x&=\arccos0\\\\\implies x&=-\dfrac{\pi }{2}, \dfrac{\pi }{2}\end{aligned}\)
Therefore, the curve of the function is:
Below the x-axis between -π and -π/2.Above the x-axis between -π/2 and π/2.Below the x-axis between π/2 and π.So to calculate the total area, we need to calculate the positive and negative areas separately and then add them together, remembering that if you integrate a function to find an area that lies below the x-axis, it will give a negative value.
Integrate the function between -π and -π/2.
As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:
\(\begin{aligned}A_1=-\displaystyle \int^{-\frac{\pi}{2}}_{-\pi} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=- \left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{-\frac{\pi}{2}}_{-\pi}\\\\&=-\dfrac{2}{3}\sqrt{4+3 \sin \left(-\frac{\pi}{2}\right)}+\dfrac{2}{3}\sqrt{4+3 \sin \left(-\pi\right)}\\\\&=-\dfrac{2}{3}\sqrt{4+3 (-1)}+\dfrac{2}{3}\sqrt{4+3 (0)}\\\\&=-\dfrac{2}{3}+\dfrac{4}{3}\\\\&=\dfrac{2}{3}\end{aligned}\)
Integrate the function between -π/2 and π/2:
\(\begin{aligned}A_2=\displaystyle \int^{\frac{\pi}{2}}_{-\frac{\pi}{2}} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&= \left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{\frac{\pi}{2}}_{-\frac{\pi}{2}}\\\\&=\dfrac{2}{3}\sqrt{4+3 \sin \left(\frac{\pi}{2}\right)}-\dfrac{2}{3}\sqrt{4+3 \sin \left(-\frac{\pi}{2}\right)}\\\\&=\dfrac{2}{3}\sqrt{4+3 (1)}-\dfrac{2}{3}\sqrt{4+3 (-1)}\\\\&=\dfrac{2\sqrt{7}}{3}-\dfrac{2}{3}\\\\&=\dfrac{2\sqrt{7}-2}{3}\end{aligned}\)
Integrate the function between π/2 and π.
As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:
\(\begin{aligned}A_3=-\displaystyle \int^{\pi}_{\frac{\pi}{2}} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&= -\left[\dfrac{2}{3}\sqrt{4+3\sin x}\right]^{\pi}_{\frac{\pi}{2}}\\\\&=-\dfrac{2}{3}\sqrt{4+3 \sin \left(\pi\right)}+\dfrac{2}{3}\sqrt{4+3 \sin \left(\frac{\pi}{2}\right)}\\\\&=-\dfrac{2}{3}\sqrt{4+3 (0)}+\dfrac{2}{3}\sqrt{4+3 (1)}\\\\&=-\dfrac{4}{3}+\dfrac{2\sqrt{7}}{3}\\\\&=\dfrac{2\sqrt{7}-4}{3}\end{aligned}\)
To evaluate the definite integral, sum A₁, A₂ and A₃:
\(\begin{aligned}\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3\sin x}}\; \text{d}x&=\dfrac{2}{3}+\dfrac{2\sqrt{7}-2}{3}+\dfrac{2\sqrt{7}-4}{3}\\\\&=\dfrac{2+2\sqrt{7}-2+2\sqrt{7}-4}{3}\\\\&=\dfrac{4\sqrt{7}-4}{3}\\\\ &\approx2.194\; \sf (3\;d.p.)\end{aligned}\)
Now we have evaluated the definite integral, we can subtract it from 3 to evaluate the given expression:
\(\begin{aligned}3-\displaystyle \int^{\pi}_{-\pi} \dfrac{\cos x}{\sqrt{4+3 \sin x}}\; \text{d}x&=3-\dfrac{4\sqrt{7}-4}{3}\\\\&=\dfrac{9}{3}-\dfrac{4\sqrt{7}-4}{3}\\\\&=\dfrac{9-(4\sqrt{7}-4)}{3}\\\\&=\dfrac{13-4\sqrt{7}}{3}\\\\&\approx 0.806\; \sf (3\;d.p.)\end{aligned}\)
Therefore, the given expression cannot be zero.

A movie website offers one free movie viewing to anyone that registers. The total number of people that register can be modeled by the function f(x)=−27x^3−135x^2−72x+220, where x is the number of months passed since starting the website. The number of free movies available to choose from can be modeled as 3x+11. Write an expression that can be used to determine the average number of people that watch each free movie. Simplify your answer.
Answers
The expression that can be used to determine the average number of people that watch each free movie is -
y = - 81x⁴ - 405x³ - 216x² + 660x - 281x³ - 1485x² - 792x + 2420
What is algebraic expression?An algebraic expression is a combination of terms both constants and variables. For example -
2x + 3y + z
3x + y
Given is that a movie website offers one free movie viewing to anyone that registers. The total number of people that register can be modeled by the function f(x) = - 27x³ - 135x² - 72x + 220, where x is the number of months passed since starting the website. The number of free movies available to choose from can be modeled as 3x + 11.
The expression that can be used to determine the average number of people that watch each free movie can be written as -
y = (- 27x³ - 135x² - 72x + 220)(3x + 11)
y = 3x(- 27x³ - 135x² - 72x + 220) + 11(- 27x³ - 135x² - 72x + 220)
y = - 81x⁴ - 405x³ - 216x² + 660x - 281x³ - 1485x² - 792x + 2420
Therefore, the expression that can be used to determine the average number of people that watch each free movie is -
y = - 81x⁴ - 405x³ - 216x² + 660x - 281x³ - 1485x² - 792x + 2420
To solve more questions on algebraic expressions, visit the link below
brainly.com/question/29014197
#SPJ1
What integer represents a $11 withdrawal?
Answers
Answer:
-11
Step-by-step explanation:
When you withdraw, you take away, so it is a negative value.
Answer: -11
Simplify 25a/8 x 2a/5
Answers
Answer:
If the slashes mean divisions and the x means multiplication, the answer would be 25a²/4/5
HURRY PLEASE ILL GIVE POINTS

Answers
2x= 15-3
2x= 12
Answer= 2
Un numero disminuido en 18 es igual a uno. Cual es el nume
Answers
Answer:
19
Step-by-step explanation:
18 + 1 = 19
What number groups does 15 classify into? Counting numbers, whole numbers, integers, rational numbers, real numbers?
Answers
Answer:
Hey, I think you've done this already!
Step-by-step explanation:
Answer:
brainliest
Step-by-step explanation:
find the value of x in the figure

Answers
Answer:
the value of y = 160
Step-by-step explanation:
exterior angle=sum of two opposite interior angle
y=(180-50)+30
y=160
what is the measure of x

Answers
Answer:
x = 9 inches
Step-by-step explanation:
You want the value of x in the similar triangles shown.
ProportionCorresponding sides are proportional. This means the ratio of the horizontal side of the triangle to the vertical side is the same for both.
6/4 = (6+x)/10
15 = 6 +x . . . . . . . . multiply by 10
9 = x . . . . . . . . . subtract 6
The measure of x is 9 inches.
__
Additional comment
You could also write the proportion ...
6/4 = x/(10 -4)
x = 36/4 = 9 . . . . . . . multiply by 6
You can see this if you draw a horizontal line through the figure at the top of the side marked 4 in.
<95141404393>
16) Solve for side AB.
AB-
Round your answer to the nearest hundredth.
A) 5.45
B) 6.45
C) 7.45

Answers
Answer:
AB= 7.45
Anwer C)
Step-by-step explanation:
Cos (angle) = Nearest side / Huypothenuse
Cos(20) = 7 / AB
Cos(20) * AB = (7 /AB) * AB
Cos (20) * AB = 7
(Cos(20) *AB) / Cos(20) = 7 / Cos(20)
AB = 7 / cos(20)
AB= 7.45
In order to find the hypotenuse, we can use the trigonometric function “cosine”,
since.
Cosine =
Adjacent side (which is 7) / hypotenuse
Cos(50) = 7 / AB
AB = 7 / Cos(50)
AB = 10.89006678802289
AB ≈ 10.89
Have a good day ^^
Use the given zero to find the remaining zeros of the polynomial function.
P(x) = 2x3 − 5x2 + 6x − 2; 1 + i
Answers
Using the given zero . The three zeros of the polynomial function are 1 + i, 1 - i, 1/2, and 2.
What is the polynomial function?If 1 + i is a zero of the polynomial function P(x), then its conjugate, 1 - i, must also be a zero of the polynomial, since complex zeros of polynomial functions with real coefficients always come in conjugate pairs.
To find the remaining zero, we can use polynomial division or synthetic division to divide P(x) by (x - 1 - i)(x - 1 + i), which is the quadratic factor corresponding to the two known zeros:
2x^2 - 3x + 2
P(x) = --------------
(x - 1 - i)(x - 1 + i)
Now we need to solve for the roots of the quadratic factor 2x^2 - 3x + 2. We can use the quadratic formula:
x = [3 ± sqrt(9 - 4*2*2)] / (2*2)
= [3 ± sqrt(1)] / 4
= 1/2 or 2
Therefore, the remaining zeros of P(x) are 1/2 and 2. The three zeros of the polynomial function are 1 + i, 1 - i, 1/2, and 2.
Learn more about polynomial function here:https://brainly.com/question/2833285
#SPJ1
you're valuing horn of plenty mining, inc.'s, stock in order to compare its value to its market price. you believe that the company will pay total dividends of $1.45 in 2015 and $1.56 in 2016. you also believe the company's stock price will be $35.80 at the end of 2016. if the appropriate discount rate is 12 percent, what's the value of horn of plenty mining's stock? a. $39.22 b. $38.31 c. $36.87 d. $37.43
Answers
Step 1: Calculate the present value of each dividend payment.
PV(2015) = $1.45 / (1 + 0.12)^1 = $1.29
PV(2016) = $1.56 / (1 + 0.12)^2 = $1.22
Step 2: Calculate the present value of the expected stock price at the end of 2016.
PV(2016 stock price) = $35.80 / (1 + 0.12)^2 = $28.33
Step 3: Add up the present values of the dividend payments and stock price to get the total stock value.
Stock value = PV(2015) + PV(2016) + PV(2016 stock price) = $1.29 + $1.22 + $28.33 = $30.84
Therefore, the value of Horn of Plenty Mining's stock is $30.84, which means that the correct option is e) None of the above.
hi, please help me with this thank you!

Answers
What is the area , rounded to nearest hundredth?

Answers
Answer:
57
Step-by-step explanation:
Area of rectangle:
4 x 12
=48
Area of left triangle:
2 x 3 / 2
=3
Area of right triangle:
6 x 2 / 2
=6
Total Area:
48 + 3 + 6 = 57
Answer: 100
Step-by-step explanation: 4 * 12 = 48 6 * 2 / 0.5 = 24 3 * 2 / 0.5 = 12
48+24+12=84 84 to the nearest hundred is 100.
Shown below is a wooden six-sided (hexagon) frame. Which of
the following best approximates the slopes of the six line
segments?
O The slopes are approximately -1.4, 0, and 1.4.
O The slopes are approximately -1.7, 0, and 1.7.
O The slopes are approximately -1.8, 1, and 1.4.
O The slopes are approximately -1.7,0, and 1.4

Answers
The slopes are best approximated as: The slopes are approximately -1.7, 0, and 1.7.
How to find the slope between two coordinates?The formula to find the slope between two coordinates is expressed as:
Slope = (y₂ - y₁)/(x₂ - x₁)
The slope of each line above the x-axis are:
Slope 1 = (5 - 0)/(5 - 8)
Slope 1 = -1.7
Slope 2 = (5 - 5)/(5 - (-2))
Slope 2 = 0
Slope 3 = (5 - 0)/(-2 - (-5))
Slope 3 = 5/3 = 1.7
Read more about slope between two coordinates at: https://brainly.com/question/3493733
#SPJ1
Evaluate the expression: 8 ⋅ (1/2)^2
Answers
Answer:
8 × (1/2)²
8 × 0.25
2 Answer!
Hope this helps, thank you :) !!
Answer:
Step-by-step explanation:
The answer is : 2
Simplify
I added image with explation! Hope this helps!
