an art teacher time his students in minutes to see how long it takes them to pain 12 inch canvas he makes a box plot for the data.how long could a student take to paint their canvas if they are slower than 75% of the other students?A-15 minutesB- 25 minutesC- 40 minutesD- 46 minutes

Answers
From the box plot, the upper quartile is 45 minutes
75 % of other students represents the upper quartile of the distribution
If the student is slower than 75% of the time taken by other students, this means the student took more time than 45 minutes
Hence, the correct answer from the options is 46 minutes
Related Questions
SECONDARY MATH III // MODULE 5
MODELING WITH GEOMETRY - 5.5
Answers
Answer:
Its Spring break pls relax
Step-by-step explanation:
Task 8: Solving for Systems of Linear Equations: Determining "intersection" point.
By successfully writing equations to define each red line, you are now to solve for where those
lines might meet on your coordinate grid.
•
●
●
Select two lines, preferably two that cross on your blueprint, and use the substitution
method to solve for their intersection point.
Mark each intersection point using a YELLOW POINT on your blueprint.
Repeat this for a total of three intersecting lines.
Example problem:
Y = -2X + 14 and Y = 3X-7
Intersection point = (4.2, 5.6)
-2X+14=3X-7
-2X=3X-21
5X=-21
X = 4.2
Y = -2(4.2) + 14
Y = -8.4 + 14
Y = 5.6

Answers
Marking the intersection points on the blueprint with yellow points:
Intersection point of Equations 1 and 2: (7, 0)Intersection point of Equations 1 and 3: (11.2, -8.4)Intersection point of Equations 2 and 3: (3.6, 3.8)How to determine intersection point?To solve for the intersection points of three lines.
Equation 1: Y = -2X + 14
Equation 2: Y = 3X - 7
Equation 3: Y = 0.5X + 2
To find the intersection point of Equations 1 and 2, use the substitution method.
Substituting Equation 1 into Equation 2:
-2X + 14 = 3X - 7
Adding 2X and subtracting 14 from both sides:
-2X + 2X + 14 = 3X + 2X - 7 - 14
14 = 5X - 21
Adding 21 to both sides:
14 + 21 = 5X
35 = 5X
Dividing both sides by 5:
X = 7
Now substitute X = 7 back into Equation 1 to find the corresponding Y value:
Y = -2(7) + 14
Y = -14 + 14
Y = 0
Therefore, the intersection point of Equations 1 and 2 is (7, 0).
To find the intersection point of Equations 1 and 3, use the same substitution method.
Substituting Equation 1 into Equation 3:
-2X + 14 = 0.5X + 2
Adding 2X and subtracting 14 from both sides:
-2X + 2X + 14 = 0.5X + 2X - 14
14 = 2.5X - 14
Adding 14 to both sides:
14 + 14 = 2.5X
28 = 2.5X
Dividing both sides by 2.5:
X = 11.2
Now substitute X = 11.2 back into Equation 1 to find the corresponding Y value:
Y = -2(11.2) + 14
Y = -22.4 + 14
Y = -8.4
Therefore, the intersection point of Equations 1 and 3 is (11.2, -8.4).
To find the intersection point of Equations 2 and 3, substituting Equation 2 into Equation 3:
3X - 7 = 0.5X + 2
Subtracting 0.5X and adding 7 to both sides:
3X - 0.5X = 0.5X + 2 + 7
2.5X = 9
Dividing both sides by 2.5:
X = 3.6
Now substitute X = 3.6 back into Equation 2 to find the corresponding Y value:
Y = 3(3.6) - 7
Y = 10.8 - 7
Y = 3.8
Therefore, the intersection point of Equations 2 and 3 is (3.6, 3.8).
Find out more on intersection point here: https://brainly.com/question/30429663
#SPJ1
STAINED GLASS Pablo made the stained glass
window shown. He used an inscribed square and
equilateral triangle for the design.
a. Label the angle measures on the outer edge of the
triangle.
b. Label all of the arcs with their degree measure.

Answers
a) The angles outside the side PQ measure 65° and 25°
The angles outside the side QR measure 85° and 95°
The angles outside the side PR measure 55° and 35°
b) The arc PR, PQ and PR measure 120°
a)
Let us assume that the inscribed square be ABCD and equilateral triangle is PQR.
Let side PR of triangle intersects the quadrilateral at points M and N.
So, we get a triangle DMN outside the equilateral triangle.
Here, ∠DMN = 55°, ∠D = 90°
So, ∠MND = 180 - (90 + 55)
= 35°
Similarly, side PQ of triangle PQR intersects the quadrilateral at points X and Y.
So, we get a triangle AXY outside the equilateral triangle.
From triangle PXM we get the measure of angle PXM which is 65 degrees.
As angle PXM and angle AXY are opposite angles, the measure of angle AXY = 65°
∠A = 90°
So, ∠AYX = 180° - (∠A + ∠AXY )
= 180° - (90° + 65°)
= 25°
Let the side QR of triangle PQR intersects the quadrilateral at points L and K.
so we get new quadrilateral LKBC
In this quadrilateral ∠B = 90°, ∠C = 90°
From triangle QYL, we get the measure of angle QLY = 95°
So, the measure of ∠KLB = 95° .......(∠QLY and ∠KLB opposite angles)
So, the remaining angle LKC of quadrilateral LKBC would be,
∠LKC = 360° - (∠B + ∠C + ∠KLB)
∠LKC = 360° - (90 °+ 90° + 95°)
∠LKC = 85°
b)
We know that he angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
so, the measure of arc PR = 120°
the measure of arc PQ = 120°
the measure of arc RQ = 120°
Learn more about the triangle here:
https://brainly.com/question/14965331
#SPJ1

Select the correct answer.
Select the correct type of sequence and recursive function for the sequence below,
34, 40, 46, 52
Answers
Answer:
f(1)=34 ; f(n)= f(n-1) +6, for n >2
Step-by-step explanation:
arithmetic sequence
In the sahara desert one day it was 146 degrees F .in the Gobi desert the temperature of - 54 degrees f was recorded what is the difference between these two temperature
Answers
Answer:
200
146- (-54)= 200
or use a number line
Calculate the average rate of change for the given function, from x = −3 to x = 7.

Answers
Answer:
The average rate of change for the given function, from x = −3 to x = 7 will be:
Average rate = -5Step-by-step explanation:
Given the table
x f(x)
-3 50
3 10
7 0
As the interval is from x = -3 to x = 7.
so
at x₁ = -3, f(x₁) = 50
at x₂ = 7, f(x₂) = 0
Using the formula to determine the average rate of change at which the total cost increases will be:
Average rate = [f(x₂) - f(x₁)] / [ x₂ - x₁]
= [0 - 50] / [7-(-3)]
= [-50] / [7+3]
= -50 / 10
= -5
Therefore, the average rate of change for the given function, from x = −3 to x = 7 will be:
Average rate = -5Please i need the answer fast k12
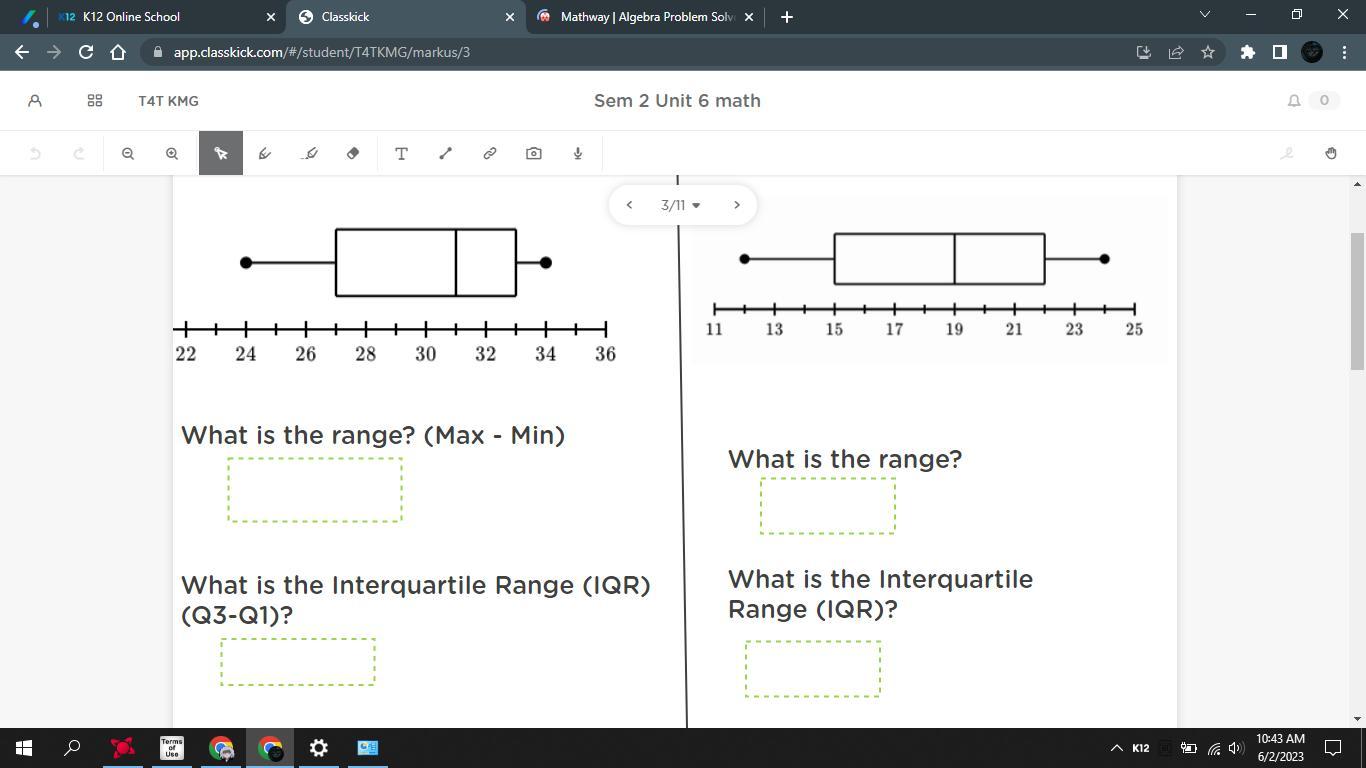
Answers
(A) The range and IQR for boxplot 1 is 10 and 6 respectively.
(B) The range and IQR for boxplot 2 is 12 and 7 respectively.
What is the IQR?The interquartile range defines the difference between the third and the first quartile.
The formula for the interquartile range is given below.
Interquartile range = Upper Quartile – Lower Quartile = Q3 – Q1
What is the range?The range is the difference between the lowest and highest values.
The formula for the interquartile range is given below.
Range = Maximum – Minimum
(A) For boxplot 1, we need to find the range and IQR from the given data set.
So, let 34 be the maximum and 24 be the minimum.
\(\text{Range}=\sf 34-24\)
\(\text{Range}=\sf10\)
Therefore, the range is 10.
Now time to find the IQR.
So, let 33 be Q3 and 27 be Q1.
\(\text{IQR}=\sf 33-27\)
\(\text{IQR}=\sf 6\)
Therefore, the IQR is 6.
(B) Now for boxplot 2, we will do the same thing as from part A.
Let's find the range.
So, let 24 be the maximum and 12 be the minimum.
\(\text{Range}=\sf 24-12\)
\(\text{Range}=\sf12\)
Hence, the range is 12.
Now for the IQR.
So, let 22 be Q3 and 15 be Q1.
\(\text{IQR}=\sf 22-15\)
\(\text{IQR}=\sf 7\)
Hence, the IQR is 7.
To know more about the range and IQR, visit:
https://brainly.com/question/31752116
#SPJ5
The length of the diagonal of a squere is 36 feet. Find the length of the side of the square.
Answers
Answer:
Length of the side of a square is 18 sqrt(2)
Step-by-step explanation:
a and b are the sides of square and c is the diagonal.
a^2+b^2=c^2
a^2+b^2= 36^2
As all sides are equal we can take b=a
2a^2=36^2
a^2= (36×36)/2
a^2 = 18×36 = 2×9×9×4
Taking squareroot on both sides we get
a= sqrt(2×9×9×2×2)
a=18 sqrt(2)
Meg makes a dot plot for the data 9, 9, 4, 5, 5, 3,
4,5, 3, 8, 8, 5. Where does a gap occur?
Answers
The gap consists of the values 6 and 7.
Check out the dot plot below to see what I mean. We have one cluster on the left from 3 to 5. Then another cluster on the right from 8 to 9.

Answer:
The gap is present around 6 & 7
Step-by-step explanation:
Since there is no evidence of dots above 6 & 7, there must have been a freeze in data around then, called a gap.
im having trouble with this one

Answers
Answer:
18
Step-by-step explanation:
90 degree angle so
90-54=36
36 / 2 = 18

As the CAPS document outlines, the Content Specification and Content Clarification for Patterns, Functions, and Algebra shows sequenced mathematics content topics and a content area spread. In the Intermediate Phase, select one topic and report on the topic sequence and content area spread. Your report should demonstrate mathematics concepts and procedures’ hierarchical and logical progression.
Answers
Answer:
Step-by-step explanation:
In the Intermediate Phase of mathematics education, one topic that demonstrates a hierarchical and logical progression in patterns, functions, and algebra is the concept of "Linear Equations."
The topic of Linear Equations in the Intermediate Phase builds upon the foundation laid in earlier grades and serves as a stepping stone towards more advanced algebraic concepts. Here is an overview of the topic sequence and content area spread for Linear Equations:
Introduction to Variables and Expressions:
Students are introduced to the concept of variables and expressions, learning to represent unknown quantities using letters or symbols. They understand the difference between constants and variables and learn to evaluate expressions.
Solving One-Step Equations:
Students learn how to solve simple one-step equations involving addition, subtraction, multiplication, and division. They develop the skills to isolate the variable and find its value.
Solving Two-Step Equations:
Building upon the previous knowledge, students progress to solving two-step equations. They learn to perform multiple operations to isolate the variable and find its value.
Writing and Graphing Linear Equations:
Students explore the relationship between variables and learn to write linear equations in slope-intercept form (y = mx + b). They understand the meaning of slope and y-intercept and how they relate to the graph of a line.
Systems of Linear Equations:
Students are introduced to the concept of systems of linear equations, where multiple equations are solved simultaneously. They learn various methods such as substitution, elimination, and graphing to find the solution to the system.
Word Problems and Applications:
Students apply their understanding of linear equations to solve real-life word problems and situations. They learn to translate verbal descriptions into algebraic equations and solve them to find the unknown quantities.
The content area spread for Linear Equations includes concepts such as variables, expressions, equations, operations, graphing, slope, y-intercept, systems, and real-world applications. The progression from simple one-step equations to more complex systems of equations reflects a logical sequence that builds upon prior knowledge and skills.
By following this hierarchical progression, students develop a solid foundation in algebraic thinking and problem-solving skills. They learn to apply mathematical concepts and procedures in a systematic and logical manner, paving the way for further exploration of patterns, functions, and advanced algebraic topics in later phases of mathematics education.
Divide four people into three rooms, in which only one room could host two people. How many ways are there to arrange them so that A, B are not in the same room
Answers
Step-by-step explanation:
AC B D
AD B C
A BC D
A BD C
hope it's right
Enter the equation of a circle that is congruent to circle C and is centered at point P

Answers
The equation of a circle that is congruent to circle C and is centered at point P is (x - 5)² + (y - 1)² = 5².
What is the equation of a circle?In Geometry, the standard form of the equation of a circle is modeled by this mathematical equation;
(x - h)² + (y - k)² = r²
Where:
h and k represent the coordinates at the center of a circle.r represent the radius of a circle.Based on the information provided, we have the following parameters for the equation of this circle:
Center (h, k) of P = (1, 5)Radius (r) of P = 5 units.By substituting the given parameters, we have:
(x - h)² + (y - k)² = r²
(x - 5)² + (y - 1)² = 5²
Read more on equation of a circle here: brainly.com/question/15626679
#SPJ1
Cost of car = $3,800
Years driven = 6
Trade-in value = $1,250
Average yearly depreciation?
Answers
Answer:
the answer is monkey epaulets monkey
Step-by-step explanation:
123
PLZ HELP
Solve each equation.
a.(8.5) ⋅ (- 3) = a
b.(- 7) + b = (-11)
c.c - (- 3) = 15
d.d⋅ (-4) = 32
Answers
Answer:
\(a = - 25.5 \\ b = - 4 \\ c = 12 \\ d = - 8\)
Charlie made hamburgers
for his family and they
each had a diameter of 7
cm. If he made 12
hamburgers. What is the
total area for all 12?
Answers
Answer:
461.58
Step-by-step explanation:
Find the mean and standard deviation of the given probability distribution. Round your answers to 2 places after the decimal point, if necessary.
x
P (x)
0
0.04
1
0.24
4
0.35
5
0.16
7
0.21
Mean =
Standard deviation =
Answers
The formula for calculating the mean of a probability distribution is mean = (x * P(x)), where x denotes a potential result and P(x) denotes its probability.
How can the probability distribution be discovered?Distribution of Probabilities F(x) = P (X x) is a formula that describes it. Additionally, if the interval (a, b) is semi-closed, the probability distribution function is provided by the equation P(a X b) = F(b) - F (a). The range of a random variable's probability distribution function is always from 0 to 1.
Therefore, the mean for this distribution is: (0 * 0.04) + (1 * 0.24) + (4 * 0.35) + (5 * 0.16) + (7 * 0.21). mean = 0 + 0.24 + 1.4 + 0.8 + 1.47 mean = 4.81
Standard deviation = ((x - mean)2 * P(x)), where x is a conceivable outcome and P(x) is the probability of that outcome, gives the standard deviation of a probability distribution.
This gives us the following standard deviation for this distribution: standard deviation = ((((0 - 4.81)2 * 0.04) + ((1 - 4.81)2 * 0.24) + ((4 - 4.81)2 * 0.35) + ((5 - 4.81)2 * 0.16) + ((7 - 4.81)2 * 0.21)) (23.0461) 4.8114 is the standard deviation.
To two decimal places, round:
mean = 4.81 4.81 is the standard deviation.
Therefore, the provided probability distribution's mean and standard deviation are 4.81 and 4.81, respectively.
To learn more about probability distribution here:
https://brainly.com/question/14210034
#SPJ1
Find the slope of the line passing through the points (1, -1) and (4, -2).
Answers
Answer:
\(slope=-\frac{1}{3}\)
Step-by-step explanation:
To find the slope of the two points (1, -1) and (4, -2) we have to use the slope formula.
\(slope=\frac{y_{2}- y_{1} }{x_{2} -x_{1} }\) \(slope=\frac{(-2)- (-1)}{4 -1}\)
\(slope=\frac{-1 }{3}=-\frac{1}{3}\) can also be written as a decimal \(slope=-0.333333\)
Which inequality is represented by the number line graph?

Answers
Answer:
x ≥ -3
Step-by-step explanation:
The shaded circle means it is equal to as well.
Question 3 Write each fraction as an equivalent fraction with the denominator 30. Then write the
original fractions in descending order
1/15, 5/6 , 7/10, 1/2
Answers
Answer: 5/6, 7/10, 1/2, 1/15
Step-by-step explanation:
5/6=25/30, 7/10=21/30, 1/2=15/30, 1/15=2/30
How many solutions does this system have? no solutions one unique solution O O two solutions O or an infinite number of solutions

Answers
Answer:
no solutions
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
equation of blue line is y = x + 2 , in slope- intercept form
with slope m = 1
equation of red line is y = x - 3 , in slope- intercept form
with slope m = 1
• Parallel lines have equal slopes
then the blue and red lines are parallel.
the solution to the system is at the point of intersection of the 2 lines
since the lines are parallel then they do not intersect each other.
thus the system shown has no solution.
for
If a study determines the difference in average salary
subpopulations of mechanical engineers and civil
engineers is NOT significant, then the subpopulations
of mechanical and civil engineers are
different
salaries.
A
Guaranteed not to be earning
B
Not earning
C) Earning very
D Definitely earning
Answers
A mean is an arithmetic average of a set of observations. The correct option is B.
What is Mean?A mean is an arithmetic average of a set of observations. it is given by the formula,
Mean = (Sum of observations)/Number of observations
The average pay does not differ significantly since the average wage for subpopulations is not significant. As a result, the subpopulations of mechanical and civil engineers are Not earning different salaries.
Hence, the correct option is B.
Learn more about Mean:
https://brainly.com/question/16967035
#SPJ1
50 students in the fourth grade class list of their hair and eye colors in the table below are the events green eyes and brown hair independent
Answers
Answer:
câu này là 500 nhen
Give the probability distribution for X:
x 0 1 2 3
f(x) 1/4 1/8 1/2 1/8
Find Var.
Answers
Answer:
Var(x)=1
Step-by-step explanation:
x p(x) x² x*p(x) x²*p(x)
0 1/4 0 0 0
1 1/8 1 1/8 1/8
2 1/2 4 1 2
3 1/8 9 3/8 9/8
Total 3/2 13/4
The required variance can be computed as
Var(x)=sumx²*p(x)-(sum(x*p(x)))²
Var(x)=13/4-(3/2)²
Var(x)=13/4-9/4
Var(x)=4/4
Var(x)=1
Thus, the required variance is 1.
Over 4 days the temperature was 4, 6, -12, and -5 degrees. What was the average temperature?
Answers
Answer:
-1.75
Step-by-step explanation:
add -12 and -5, you get -17, and 4 and 6, get 10, add -17 and 10 to get -7, and divide by 4 and get -1.75
PLEASE HELP ASAP
The diagrams show a polygon and the image of the polygon after a transformation.
Use the diagrams to determine which statements are true. Select all statements that are true.

Answers
The correct statements regarding the transformations are given as follows:
Parallel lines will always be parallel after a reflection.Lines that are not parallel will never be parallel after a translation.What are transformations on the graph of a function?Examples of transformations are given as follows:
A translation is defined as lateral or vertical movements.A reflection is either over one of the axis on the graph or over a line.A rotation is over a degree measure, either clockwise or counterclockwise.For a dilation, the coordinates of the vertices of the original figure are multiplied by the scale factor, which can either enlarge or reduce the figure.Parallel lines are lines that have the same slope, that is, lines that do not intercept, and the transformations do not change whether the lines are parallel or not.
More can be learned about transformations in a figure at https://brainly.com/question/28687396
#SPJ1
What is the perimeter of the shape below? Use 3.14 for pi. Answer with numbers only, no units.
DO NOT ROUND THE ANSWER

Answers
Step-by-step explanation:
The circumference of a WHOLE circle = pi * d
you have 1/2 of this and d = 10 ft
so 1/2 pi * 10 PLUS the two straight sides + 8+6
1/2 pi * 10 + 8 + 6
5 pi + 8 + 6
5 * 3.14 + 14 = 29.7 ft
Suppose that v varies directly with x, and v = 20 when x = 32.
A) Write a direct variation equation that relates x and y .
B) Find y when x = 24
Answers
\(\qquad \qquad \textit{direct proportional variation} \\\\ \textit{\underline{y} varies directly with \underline{x}}\qquad \qquad \stackrel{\textit{constant of variation}}{y=\stackrel{\downarrow }{k}x~\hfill } \\\\ \textit{\underline{x} varies directly with }\underline{z^5}\qquad \qquad \stackrel{\textit{constant of variation}}{x=\stackrel{\downarrow }{k}z^5~\hfill } \\\\[-0.35em] ~\dotfill\)
\(\stackrel{\textit{"v" varies directly with "x"}}{v = k(x)}\hspace{5em}\textit{we also know that} \begin{cases} x=32\\ v=20 \end{cases} \\\\\\ 20=k(32)\implies \cfrac{20}{32}=k\implies \cfrac{5}{8}=k\hspace{8em}\boxed{v=\cfrac{5}{8}x} \\\\\\ \textit{when x = 24, what's v?}\qquad v=\cfrac{5}{8}(24)\implies v=15\)
y varies directly with x.
y is -50 when x is 10
What is x when y is 15?
Suppose
x = [?]
X
Answers
The value of x is -3 when value of y = 15 by using the property proportion as x and y are directly related to each other.
What is direct relation?
Two variables x and y are directly related to each other if x increases or decreases the value of y also increases or decreases proportionally.
We are given that value of y is -50 then value of x is 10
We have to find the value of x when y is 15
We solve it using proportion
we have,
10/x = -50/15
On separating the variable from the constant and then simplifying we get,
x=-3
Hence the value of x is -3 when y is 15
To learn more about proportions please refer the following link
https://brainly.com/question/19994681
#SPJ13
deduct for thousand eleven hundred and a half from twelve thousand twelve hundred and twelve
Answers
Answer:
8111.5
Step-by-step explanation:
Deduct for thousand eleven hundred and a half from twelve thousand twelve hundred and twelve
Rewriting the above question in figure :
4000 + 100 + 0.5 = 5100.5
12000 + 1200 + 12 = 13212
13212 - 5100.5 = 8111.5
= 8111.5