An aquarium can be modeled as a right rectangular prism and it can hold 540 cubic inches of water when it is full. Its width is 6 in and height is 5 in. Find the length of the aquarium in inches. Round your answer to the nearest tenth if necessary.
Answers
The required length of the right rectangular prism is 18 in whose volume is 540 cu. in
What is a rectangular prism?Having six faces, a rectangular prism is a three-dimensional shape (two at the top and bottom and four are lateral faces). The prism's faces are all rectangular in form. There are three sets of identical faces as a result. A rectangular prism is often referred to as a cuboid because of its form. A rectangular prism may be found in everyday objects like a geometry box, notebooks, diaries, and rooms.
Rectangular prism characteristics
There are 6 faces, 12 edges, and 8 vertices on a rectangular prism.The rectangular prism's top and bottom are always rectangles.It has three dimensions, or length, breadth, and height, much like a cuboid.opposing face pairs are identical or coincidentThe lateral sides of a right rectangular prism are rectangle-shaped.The lateral faces of an oblique rectangular prim are parallelograms.Its cross-section is rectangular in shape.It has a perfect cuboid appearance.There are two categories into which rectangular prisms can be divided. These are:
Right Rectangular PrismOblique Rectangular PrismA rectangular prism is a prism with rectangular bases. A right rectangular prism is a prism with six rectangle-shaped faces with angles that are all right angles.
Vertices of a rectangular prism = 8
Edges of a rectangular prism = 12
Faces of a rectangular prism= 6 (including bases)
total volume of the prism = 540 cubic inches.
Width = 6 in
Height = 5 in
We know volume is length * breadth* height
⇒ 540 = 5*6* length
⇒length = 18 in
The required length of the right rectangular prism is 18 in.
To learn more about Volume and Area refer to :
https://brainly.com/question/29205933
#SPJ1
Related Questions
Use the information to diswer
The area of the triangle shown is 40.0 cm2.
?
12.5 cm
What is the height of the triangle?
A. 3.20 cm
OB. 6.40 cm
OC. 13.8 cm
OD. 27.5 cm
Answers
Explanation: Since they've given use the area of the triangle, we can use the area formula to find the base of the triangle. The formula to find the area of a triangle is: a=12hb.
Dave borrowed $600 on January 1,2022 The bonk charged him a $6.40 service charge, and interest was $44.90 if Dave paid the $600 in 12 equal monthiy payments, what was the APR? Note: Do not round intermediate calculations. Enter your answer as o percent rounded to 1 decimal place. Dorothy lacks cash to pay for a 5840.00 dishwasher. She couid buy it from the store on credit by making 12 monthly poyments of $7125. The totat cost would then be $855.00 instead. Dorothy decides to deposit $70.00 a month in the bank until the has saved enough money to pay cash for the dishwasher, One year later, she has saved $898.80−584000 in deposits plus interest When she goes back to the store, she finds the dishwasher now costs $90888 its price has gone up 820 percent. Was postponing her purchase a good trade-off for Dorothy?
Answers
The increase in price (8.20%) is less than the interest she would have paid (12 payments of $7125), it seems that postponing her purchase and saving money was a good trade-off for Dorothy.
The APR (Annual Percentage Rate) for Dave's loan can be calculated
using the formula:
APR = ((Total interest + Service charge) / Principal) * 100
In this case, the total interest is $44.90 and the service charge is $6.40.
The principal is $600. Plugging these values into the formula:
APR = (($44.90 + $6.40) / $600) * 100
Simplifying the equation:
APR = ($51.30 / $600) * 100
APR = 8.55%
For Dorothy, if she bought the dishwasher on credit, the total cost would
be $855.00 after making 12 monthly payments of $7125.
However, if she saved $70.00 a month for one year, she would have
$898.80 in deposits plus interest.
When she goes back to the store, the dishwasher now costs $908.88,
which is an increase of 8.20%.
Since the increase in price (8.20%) is less than the interest she would
have paid (12 payments of $7125), it seems that postponing her purchase
and saving money was a good trade-off for Dorothy.
To know more about Annual Percentage Rate, visit:
https://brainly.com/question/31987528
#SPJ11
What do you put on the X axis of an ogive?
Answers
The X-axis (horizontal axis) often represents a "class boundaries" of such an ogive, whereas the Y-axis (vertical axis) typically shows the frequency count.
Explain about the ogive graph?A sort of frequency polygon that displays cumulative frequencies is an ogive, often known as a cumulative frequency polygon.
In other words, the graph adds the cumulative percents from left to right.On an ogive graph, "class boundaries" are shown along the x-axis while cumulative frequency is shown on the y-axis. Comparable to a histogram, an ogive features a single point that indicates in which the top right corner of the rectangular would be located in place of rectangles. This type of graph is typically simpler to make from such a frequency table.Thus, The X-axis (horizontal axis) often represents a class boundaries being measured of such an ogive.
To know more about the ogive, here
https://brainly.com/question/2500839
#SPJ4
Sara Wants to Triple A recipe For Brownies. The recipe Calls For 1 1/3 cups of Flour. There are exactly 4 cups of flour left in the Canister. Will It be enough?? like this is like a Yes or No question.. I got my answer But I want to make sure I Got It Correct. Please Help!!
Answers
PLEASE ANSWER TOADAY !!!!!!!!!!!!!!!!!

Answers
Answer:
most likely next spring
Step-by-step explanation:
Step-by-step explanation:
6 5/15 in its simiplist form
Answers
Answer:
6 1/3
Step-by-step explanation:
Well 5 goes into 15 3 times because 5 * 3 = 15.
So the answer would be 1/3 for the fraction and 6 1/3 for the answer.
Answer:
6 1/3
Step-by-step explanation:
6 is already in its simplest form.
5/15 = 1/3
^ 5/15 is equivalent to 1/3
An ice cream cone measures 4 in across the opening of the cone. Two hemisphere shaped scoops of ice cream, which have diameters of 4in, are placed on top of the cone. As the ice cream melts, it begins to fill the ice cream cone. How deep must the cone be so that the melted ice cream will fill the cone exactly to the top without overflowing?
Answers
Answer:
8 inches
Step-by-step explanation:
The volume of a hemisphere is half the volume of a sphere.
Therefore, the sum of the volumes of the two hemisphere-shaped scoops of ice cream (with diameters of 4 inches), is equal to the volume of a sphere with diameter of 4 inches.
If the melted ice cream fills the cone exactly to the top without overflowing, the volume of the cone with diameter of 4 inches must be equal to the volume of a sphere with diameter of 4 inches.
As the diameter of a circle is twice its radius, then the radius of the sphere and cone is r = 2 inches.
The formulas for the volume of a cone and the volume of a sphere are:
\(\boxed{\begin{minipage}{4 cm}\underline{Volume of a cone}\\\\$V=\dfrac{1}{3} \pi r^2 h$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $h$ is the height.\\\end{minipage}}\) \(\boxed{\begin{minipage}{4 cm}\underline{Volume of a sphere}\\\\$V=\dfrac{4}{3} \pi r^3$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius.\\\\\end{minipage}}\)
The depth of the cone is its height.
Therefore, to calculate how deep the cone must be so that the melted ice cream will fill the cone exactly to the top without overflowing, set the two equations equal to each other, substitute r = 2, and solve for h (the depth of the cone).
\(\begin{aligned}\textsf{Volume of a cone}&=\textsf{Volume of a sphere}\\\\\dfrac{1}{3} \pi (2)^2 h & = \dfrac{4}{3} \pi (2)^3\\\\\dfrac{1}{3} \pi \cdot 4 h & = \dfrac{4}{3} \pi \cdot 8\\\\\dfrac{4}{3} \pi h& = \dfrac{32}{3} \pi \\\\\dfrac{4}{3} h& = \dfrac{32}{3} \\\\4 h& = 32 \\\\h&=\dfrac{32}{4}\\\\h&=8\; \sf inches\end{aligned}\)
Therefore, the depth of the cone must be 8 inches.
The cone must be at least 8 inches deep in order for the melted ice cream to fill the cone exactly to the top without overflowing.
1. The opening of the ice cream cone has a diameter of 4 inches. This means that the radius of the cone's opening is 4/2 = 2 inches.
2. The two hemisphere-shaped scoops of ice cream have diameters of 4 inches each. This means that the radius of each scoop is 4/2 = 2 inches.
3. When the ice cream melts, it will take up the space between the scoops and fill the cone. In order for the melted ice cream to fill the cone exactly to the top without overflowing, the depth of the cone must be equal to the combined height of the two ice cream scoops.
4. The height of each hemisphere-shaped scoop can be calculated using the formula for the volume of a sphere, which is (4/3)πr³, where r is the radius.
- For each scoop, the radius is 2 inches, so the height of each scoop is (4/3)π(2)³ = (4/3)π(8) = (32/3)π.
5. Since there are two scoops, the combined height of the two scoops is 2 * (32/3)π = (64/3)π.
6. Therefore, the cone must be at least (64/3)π inches deep in order for the melted ice cream to fill the cone exactly to the top without overflowing. This is approximately equal to 67.03 inches.
For more such questions on inches, click on:
https://brainly.com/question/876758
#SPJ8
Please answer in an hour! You will get a thumbs up.
Question 1 (a)
Assume you purchase a new tractor on Jan 1, 2022 for a cost of $200,000. You estimate you will be able to use the tractor for 10 years, and it will have a salvage value of 10% of the original by the end of its useful life. Determine the book value at the end of the first year (December 31, 2022) using straight-line depreciation.
options:
$18,000
$180,000
$185,000
$182,000
Question 1 (b)
A balance sheet (using current and noncurrent assets and liabilities- no intermediate) shows that a farmer has current assets of $80,000 and owner equity of $100,000. Her current ratio is 2 and her debt/equity ratio is 1.0. Determine the farmer's noncurrent liabilities.
Question 1 (b) options:
$40,000
$60,000
$100,000
unable to determine
Answers
Question 1a
To calculate the book value at the end of the first year using straight-line depreciation, we need to determine the annual depreciation expense first. The straight-line method assumes that the asset depreciates by an equal amount each year over its useful life. Therefore, we can use the following formula to calculate the annual depreciation:
Annual Depreciation = (Cost - Salvage Value) / Useful Life
Substituting the given values, we get:
Annual Depreciation = ($200,000 - $20,000) / 10 years = $18,000 per year
This means that the tractor will depreciate by $18,000 each year for the next 10 years.
To determine the book value at the end of the first year, we need to subtract the depreciation expense for the year from the original cost of the tractor. Since one year has passed, the depreciation expense for the first year will be:
Depreciation Expense for Year 1 = $18,000
Therefore, the book value of the tractor at the end of the first year will be:
Book Value = Cost - Depreciation Expense for Year 1
= $200,000 - $18,000
= $182,000
So the book value of the tractor at the end of the first year, December 31, 2022, using straight-line depreciation is $182,000. so the answer is D
Question 1(b)
To determine the farmer's noncurrent liabilities, we need to use the information provided to calculate the total liabilities and then subtract the current liabilities from it. Here's the step-by-step solution:
Calculate the total current liabilities using the current ratio:
Current Ratio = Current Assets / Current Liabilities
2 = $80,000 / Current Liabilities
Current Liabilities = $80,000 / 2
Current Liabilities = $40,000
Calculate the total liabilities using the debt/equity ratio:
Debt/Equity Ratio = Total Liabilities / Owner Equity
1.0 = Total Liabilities / $100,000
Total Liabilities = $100,000 * 1.0
Total Liabilities = $100,000
Subtract the current liabilities from the total liabilities to get the noncurrent liabilities:
Noncurrent Liabilities = Total Liabilities - Current Liabilities
Noncurrent Liabilities = $100,000 - $40,000
Noncurrent Liabilities = $60,000
Therefore, the farmer's noncurrent liabilities are $60,000. so the answer is B.
in a class of 40 students, 19 play tennis, 20 play netball, and 8 play neither of these sports. a student is randomly chosen from the class. determine the probability that the student:
Answers
Therefore, the probability that the student plays neither tennis nor netball is 1/5 = 0.2 or 20%.
There are 40 students in a class. 19 students play tennis, 20 students play netball, and 8 students play neither of these sports.
A student is chosen randomly from the class, and we need to determine the probability that the student: Plays tennis If a student is randomly chosen from the class, the probability that the student plays tennis is: Probability of playing tennis= (Number of students playing tennis) /
(Total number of students in the class) Probability of playing tennis= 19 / 40Plays netball if a student is randomly chosen from the class, the probability that the student plays netball is: Probability of playing netball= (Number of students playing netball) / (Total number of students in the class)Probability of playing netball= 20 / 40 = 1/2Plays neither of these sports a student is randomly chosen from the class, the probability that the student plays neither tennis nor netball is
:Probability of playing neither tennis nor netball= (Number of students who do not play either of the two sports) / (Total number of students in the class)Probability of playing neither tennis nor netball= 8 / 40Probability that the student plays tennis and netball
Probability of playing tennis and netball = (Number of students playing both tennis and netball) / (Total number of students in the class)We are given that none of the students play both tennis and netball, so the probability of playing both tennis and netball is 0.
You can read more about Probability at https://brainly.com/question/24756209
#SPJ11
im not sure how to understand this

Answers
the number of right handed students in a mathematics class is nine times the number of left hand students. the total number of students in the class is 30. how many right handed students are in the class? how many left handed students are in the class?
Answers
Answer:
3 left handed and 27 right handed.
Step-by-step explanation:
9+1=10
30/10=3
3*9=27
30-27=3
Additional Algo 8-5 Percent Value-Added Time Patients seeking care at the County General emergency room wait, on average, 14 minutes before seeing the triage nurse who spends, on average, 5 minutes assessing the severity of their problem. The most serious cases are seen first and the less serious often have to wait. On average, the wait time before being taken to the examination room is 79 minutes. In the examination room, a nurse spends about 11 minutes taking vitals and making notes on the patient's condition. The patient then waits for the doctor. This wait averages 22 minutes. Treatment times by the doctor average 17 minutes. Following treatment, patients wait 6 minutes for the nurse to come to discuss the post treatment instructions. It takes about 4 minutes to review with the patient these instructions before they leave. Considering any time spent interacting with a nurse or doctor as value-added time. What is the precent value-added time in a trip to the emergency room? Note: Round your answer as a percentage to 2 decimal places.
Answers
The percentage of value-added time in a trip to the emergency room is 15.83%.
Given the following data:
Time taken by triage nurse before assessment = 14 minutes
Average time taken for assessment by triage nurse = 5 minutes
Time taken before examination room = 79 minutes
Time taken in the examination room for vitals and notes by nurse = 11 minutes
Time taken before the doctor sees the patient = 22 minutes
Average time taken by the doctor for treatment = 17 minutes
Time taken for the nurse to come to discuss post-treatment instructions = 6 minutes
Time taken to review the instructions with the patient = 4 minutes
Let us first calculate the total time taken,
Total Time = Time before examination room + time in examination room + time after treatment + time taken by the triage nurse
Total Time = 79 + 11 + 22 + 17 + 6 + 4
= 139 minutes
Now, let us calculate the total time spent on assessment and treatment.
This will include the time taken by the triage nurse and the doctor.
Total Time Spent on Assessment and Treatment = Time taken by triage nurse + time taken by the doctor
Total Time Spent on Assessment and Treatment = 5 + 17
= 22 minutes
Now, we can calculate the percentage of value-added time as follows,
Percentage of Value-Added Time = Total Time Spent on Assessment and Treatment / Total Time * 100
Percentage of Value-Added Time = 22 / 139 * 100
Percentage of Value-Added Time = 15.83%
Therefore, the percentage of value-added time in a trip to the emergency room is 15.83%.
Rounding off this value to 2 decimal places, we get the final answer as 15.83%.
Learn more about percentage from this link:
https://brainly.com/question/24877689
#SPJ11
Pls I really need help it’s not that hard

Answers
Answer:
distributive propriety
Step-by-step explanation:
Step 1 was distributive propriety because
We distributed the multiplication between 14 and (x+5) over the addition x+5
If we have 14 multiply by a number will just do that. (e.g. 14*3= 42)
If we have 14 multiply by a number written as the sum of others we need to distribute to each part. (e.g. 14*(1+2) = 14*1 +14*2 = 14+28 = 42)
If you have less than $10.00 in dimes and quarters. Which of the following is a
possible combination of dimes and quarters that satisfy the inequality. *
a. 50 dimes and 20 quarters
b. 20 dimes and 50 quarters
c. 50 dimes and 30 quarters
d. 40 dimes and 20 quarters
Answers
Answer:
D. 40 dimes and 20 quarters
Step-by-step explanation:
40 dimes= $4 because 10 dimes= $1
20 quarters= $5 because 4 quarters= $1
The other options are above $10. I hope this helps!!!! :D
30. -3a^2= -3-6^2 is this correct? And I have to evaluate o I am not good at that so if u can help THANK YOU so much!
a=-6
Answers
Answer:
-3a^2= -3*(-6)^2
Step-by-step explanation:
-3a^2 = -3*a^2 = -3*(-6)^2
The most likely outcomes for a particular project are estimated as follows;
Unit price:
§ 80
Variable cost:
§ 60
Fixed costi
§ 440,800 Expected
sales:
40,600 units per year However, you recognize that some of these estimates are subject to error. Suppose each variable turns out to be either 5% higher or 5% lower than the initial estimate. The project will last for 10 years and requies an initial investment of $14 milion, which wil be depreciated straight line over the projeci life to a final value of
zero. The firm's tax rate is 21%, and the required rate of retum is 14%. a. What is project's NPV in the best-case scenario, that is, assuming all variables take on the best possible
value?
b. What is project's NPV in the worst-case scenario? Note: For all the requirements, a negative amount should be indicated by a minus sign. Enter your answers in dollars, not in millions. Do not round intermediate calculations. Round your answers to the
nearest dollar amount.
Answers
To calculate the project's NPV in the best-case scenario, we need to consider the best possible values for each variable.
Here are the steps-
Step 1: Calculate the annual cash inflow.
Annual revenue = Unit price * Expected sales
= $80 * 40,600
= $3,248,000
Step 2: Calculate the annual cash outflow.
Annual variable cost = Variable cost * Expected sales
= $60 * 40,600
= $2,436,000
Annual fixed cost = Fixed cost
= $440,800
Annual depreciation = Initial investment / Project life
= $14,000,000 / 10
= $1,400,000
Annual tax = (Annual revenue - Annual variable cost - Annual fixed cost - Annual depreciation) * Tax rate
= ($3,248,000 - $2,436,000 - $440,800 - $1,400,000) * 0.21
= $208,720
Step 3: Calculate the annual net cash flow.
Annual net cash flow = Annual revenue - Annual variable cost - Annual fixed cost - Annual depreciation - Annual tax
= $3,248,000 - $2,436,000 - $440,800 - $1,400,000 - $208,720
= $162,480
Step 4: Calculate the NPV using the best-case scenario cash flows.-
\(NPV = Initial investment + (Annual net cash flow / (1 + Required rate of return)^n)\)
\(= -$14,000,000 + ($162,480 / (1 + 0.14)^1) + ($162,480 / (1 + 0.14)^2) + ... + ($162,480 / (1 + 0.14)^10)\)
To know more on Revenue visit:
https://brainly.com/question/27325673
#SPJ11
Find last year’s salary if, after a 3% pay raise, this year’s salary is $32,960.
Answers
Answer:
$32000
Step-by-step explanation:
Let last years salary was $x
Therefore,
x + 3% of x = $32960
x + 0.03x = $32960
1.03x=$32960
x = 32960/1.03
x = $32,000
So, last year's salary was $32000.
are the following statements true or false? true 1. if vectors span a subspace and if is orthogonal to each for , then is in . true 2. . false 3. let and be non zero vectors. if the distance from to is equal to the distance from to , then and are orthogonal. true 4. for a square matrix , vectors in are orthogonal to vectors in . true 5. for any scalar .
Answers
The statement " For any scalar c, uT(cv) = c(uTv)" is True, as it is distributive property of matrix. The statement "u and v are orthogonal" is true as u · v = 0. The statement " vectors in R(A) are orthogonal to vectors in N(A)." is False. Vectors in R(A) are orthogonal to vectors in \(N(A)^{perpendicular}\), not to vectors in N(A) itself. The statement "(\(V^t\))*V = ||v||²" is True. (\(V^t\))*V is a p x p matrix with the diagonal elements. The last statement is True as x is orthogonal to every vector in the subspace W spanned by the \(v_i's\).
The statement is true because of the distributive property of matrix multiplication. Using the fact that (cv)u = c(vu), we have
uT(cv) = (cv)Tu = c(vTu) = c(uTv)
If the distance from vector u to vector v is equal to the distance from u to -v, then we can write it mathematically as
||u - v|| = ||u - (-v)||
Expanding the above equation, we get
||u - v|| = ||u + v||
Now, let's square both sides of the above equation
||u - v||² = ||u + v||²
Expanding the squares, we get
(u - v) · (u - v) = (u + v) · (u + v)
where "·" denotes the dot product.
Simplifying the above equation, we get
u · u - 2u · v + v · v = u · u + 2u · v + v · v
The above equation can be further simplified as
2u · v = -2u · v
Hence, we get
u · v = 0
which means that u and v are orthogonal or perpendicular to each other. Therefore, the given statement is true.
The statement is false. Consider a matrix A with a single column vector v, which is not the zero vector. Then N(A) is the set of all scalar multiples of v, and R(A) is the set of all scalar multiples of Av. Any non-zero scalar multiple of Av is not orthogonal to v, so vectors in R(A) are not necessarily orthogonal to vectors in N(A). However, it is true that vectors in R(A) are orthogonal to vectors in\(N(A)^{perpendicular}\), which is the orthogonal complement of N(A).
The statement is true. Let V be an n x p matrix with columns v₁, v₂, ..., \(v_p\). Then, (\(V^t\))*V is a p x p matrix whose (i,j)-th entry is given by the dot product of the ith and jth columns of V
(\(V^t\))*\(v_{(i,j)}\) = viT vj
If i = j, then this simplifies to ||\(v_i\)||². Otherwise, if i ≠ j, then \(v_i\) and \(v_j\) are different columns of V, so they are orthogonal and their dot product is zero. Therefore, the diagonal entries of (\(V^t\))*V are ||v₁||², ||v₂||², ..., ||\(v_p\)||².
The statement is true. Let W be the subspace spanned by the vectors v₁, v₂, ..., \(v_p\), and let x be a vector that is orthogonal to each \(v_j\). This means that x is orthogonal to every linear combination of the \(v_i's\), since such a combination is a sum of scalar multiples of the \(v_j's\). Therefore, x is orthogonal to every vector in W, which means that x is in \(W^{perpendicular}\).
To know more about orthogonal vectors:
https://brainly.com/question/30075875
#SPJ4
--The given question is incomplete, the complete question is given
" Are the following statements true or false? 1. For any scalar c, uT(cv) = c(uTv). 2. Let u and v be non zero vectors. If the distance from u to v is equal to the distance from u to -v, then u and v are orthogonal 3, For a square matrix A, vectors in R(A) are orthogonal to vectors in N(A). 4. (V^t)*V = ||v||^2, 5. If vectors vi , . . . , y, span a subspace W and if x is orthogonal to each vj for j = 1 , . . . , p, then x is in W^perpendicular?"--
What is the solution to the equation below? Round your answer to two
decimal places.
6 • e^x = 25
Answers
x = 1.43 is the solution to the equation 6 • e^x = 25, rounded to two decimal places

A coffee pot holds 6 quarts of coffee. How much is this in cups?
Answers
Answer:
24 cups
Step-by-step explanation:
1 quart = 4 cups
6x4= 24 cups
Answer:
24 cups.
Step-by-step explanation:
Each quart is equal to 4 cups. This means you have to do 6x4 to find the answer.
PLEASSE HELP
If a line crosses the y-axis at (0, 1) and has a slope of 4/5, what is the equation of the line?
A 4y - 5x=5
B.y - 4x = 5
C. 5y + 4x = 5
D. 5y - 4x = 5
Answers
Answer:
The answer is option D.Step-by-step explanation:
Equation of the line using point (0, 1) and slope 4/5 is
\(y - 1 = \frac{4}{5} (x - 0) \\ \\ 5y - 5 = 4x \\ \\ 5y - 4x = 5\)
Hope this helps you
Answer:
D. \(\boxed{5y-4x=5}\)
Step-by-step explanation:
Slope = m = 4/5
y - intercept = b = 1 (As from the point (0,1) , y-intercept is when x = 0)
So, the equation becomes
=> \(y = mx+b\)
=> \(y = \frac{4}{5} x +1\)
=> \(y - \frac{4}{5} x = 1\)
Multiplying both sides by 5
=> \(5y-4x = 5\)
selected a sample of 200 people in Wenatchee and observed that 63 prefer Taco Bell. At 0.05, is
there enough evidence to support his claim?
Justify your answer by stating what is
(a) the null hypothesis and alternative hypothesis. Explain what test (left-tailed, right-tailed or two-tailed)
you are using. Also find
(b) critical z-value (not the p-value!)
(c) test value

Answers
After answering the provided question, we can conclude thatAs a result, null hypothesis there is sufficient evidence to support John's claim that more than 25% of Wenatchee residents prefer Taco Bell.
What is null hypothesis?A null hypothesis is a type of statistical hypothesis that asserts that a specific set of observations has no statistical significance. Sample data is used to assess the viability of theories. H0 represents what is referred to as "zero" on occasion. The researchers make the assumption that there may be a relationship between the factors. The null hypothesis, which is on the other hand, claims that no such relationship exists. Although it may not appear to be significant, the null hypothesis seems to be an important part of research.
(a) p = 0.25 for the null hypothesis
p > 0.25 is an alternative hypothesis.
To test this hypothesis, we can use the z-Test for proportion.
(b) \s(c) (c) The test value can be calculated using the z-Test for proportion formula:
(p - p) / (p(1-p)/n) = z
where p represents the sample proportion, p represents the hypothesised population proportion, and n represents the sample size.
p = 63/200 = 0.315, p = 0.25, and n = 200 in this case. When we enter these values into the formula, we get:
z = (0.315 - 0.25) / √(0.25 * 0.75 / 200) = 2.34
The result of the test is 2.34.
(d) Because the test value (2.34) is greater than the critical z-value (1.645), the null hypothesis is rejected. As a result, there is sufficient evidence to support John's claim that more than 25% of Wenatchee residents prefer Taco Bell.
To know more about null hypothesis visit
https://brainly.com/question/28920252
#SPJ1
whats missing?
-(-5) = -7
Answers
Answer:
-2
Step-by-step explanation:
becuase -2 - -5=-7
Can a triangle be formed with angle measures of 51, 71, and 44?
Answers
Answer:
nope
Step-by-step explanation:
a triangle should have 180 degrees, if we add up the three angles and it doesnt equal 180 degrees, then a triangle can't be formed.
Since 51+71+44 = 166, which is not 180, these angles cannot make a triangle
3. Use the image to answer the following questions.
will brainiest if correct. try ur best!
(a) The angle pitch of a roof is safest when measuring between 18° – 27°. According to these guidelines, is the roof pictured in the image safe? (Note:
(b) What is length of the roof line (segment PR)? Round answer to the nearest tenth of a foot and show all your work.
Answer:

Answers
Answer:
Step-by-step explanation:
For missing hypotenuse: \(\sqrt({a^{2} + b^{2})\)
Plug in the side lengths that are known to find the hypotenuse.
1. No, the angle is less than 18 degrees (closer to 15), so it is not safe
2. The length rounded to the nearest tenth is approximately 15.5 feet.
Find the quotients. Answer as whole numbers or fractions.
2/5 ÷ 3/4 =
9/4 ÷ 3/4 =
5/7 ÷ (-1/-3) =
(whole fraction is negative)
-5/3 ÷ 1/6 =
if its only ‘-‘ at the numerator that means only the numerator is negative )
Answers
Answer:
ANSWERS
1st Question: 8/15
2nd Question: 3
3rd Question: -2 1/7
4th Question: -10
Used a Calculator :3 hope it helps
2nd Question: 3
3rd Question: -2 1/7
4th Question: -10
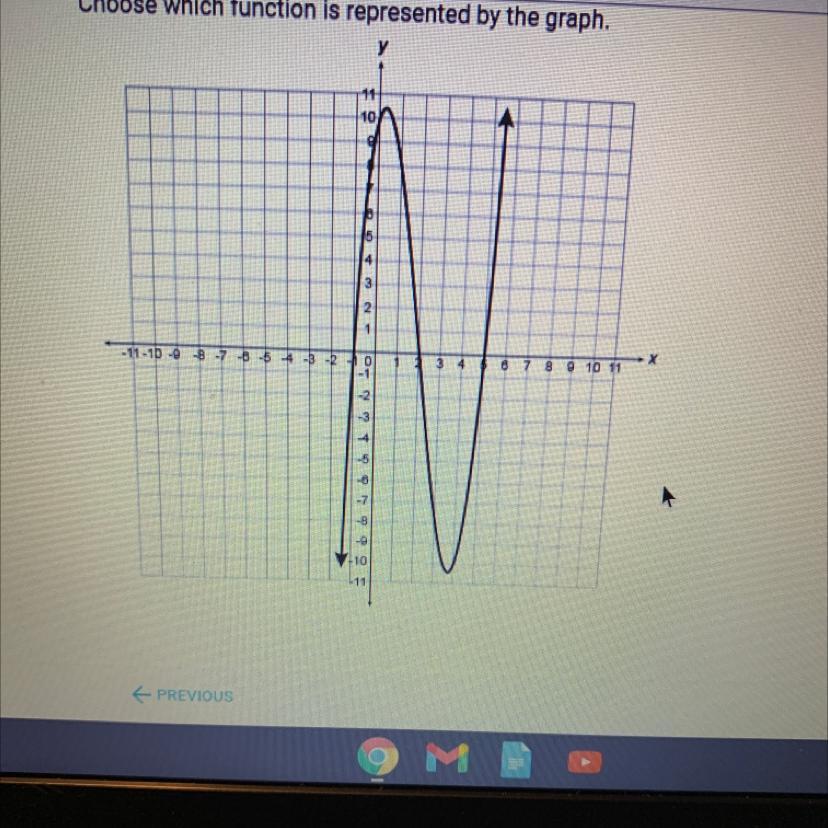
Choose which function is represented by the graph A. f(x) = (x - 1)(x + 2)(x+5)(x+10)
B. f(x) = (x - 5)(x-2)(x + 1)
C. f(x) = (x - 10)(x - 5)(x - 2)(x+1)
D. f(x) = (x - 1)(x + 2)(x+5)
Answers
Answer:
Option B
Step-by-step explanation:
From the graph attached,
x-intercepts of the graph are x = -1, 2 and 5
y-intercept of the graph is y = 10
Since, x intercepts of a graph define the zeros of the function (y = 0)
Therefore, (x + 1), (x - 2) and (x - 5) are the zero factors of the given graphs.
And the equation of the function will be,
f(x) = a(x + 1)(x - 2)(x - 5)
Since, -intercept of the function is y = 10
Therefore, for x = 0,
y = a(0 + 1)(0 - 2)(0 - 5) = 10
a(10) = 10
a = 1
So the function representing the graph is,
f(x) = (x - 1)(x + 2)(x - 5)
Option B will be the answer.
in your own words what is a polygon
Answers
Step-by-step explanation:
A polygon is a shape with at least three straight lines and angles
Find the first partial derivatives of the function. w = ln(x + 9y + 6z) partial differential w/partial differential x = partial differential w/partial differential y = partial differential w/partial differential z =
Answers
We have the function:
w = ln(x + 9y + 6z)
Taking the partial derivative with respect to x, we get:
partial w / partial x = 1 / (x + 9y + 6z) * (1)
Taking the partial derivative with respect to y, we get:
partial w / partial y = 1 / (x + 9y + 6z) * 9
Taking the partial derivative with respect to z, we get:
partial w / partial z = 1 / (x + 9y + 6z) * 6
Therefore, the first partial derivatives of w are:
partial w / partial x = 1 / (x + 9y + 6z)
partial w / partial y = 9 / (x + 9y + 6z)
partial w / partial z = 6 / (x + 9y + 6z)
For more questions like derivatives visit the link below:
https://brainly.com/question/31008281
#SPJ11
How to find the simple interest rate if P=$4,000. T=2 years . And I= $320
And pls explain how I can find simple interest in every question bc I’m stressing about math finals
Answers
Answer:
3.2
Step-by-step explanation:
Formula to find the simple interest rate :
S.I. = \(\frac{PRT}{100}\)
Formula to find R (simple interest rate) :
R = \(\frac{100*S.I.}{P*T}\)
Since you have I (interest amount), we can use this formula instead :
R = \(\frac{I}{PT}\)
R = \(\frac{320}{4,000*2}\) = 4%/year or 0.04
Now plug this into the first formula
S.I. = \(\frac{4,000*0.04*2}{100}\) = 3.2
i haven't done this in a while so hope this helps !!