An 18-foot ladder is leaning against a wall. The bottom of the ladder is 4.5 feet from the base of the wall.
How high up the wall does the ladder reach? Round your answer to the nearest tenth, if necessary.
A
13.5 feet
B
18.6 feet
o
С
22.5 feet
D
17.4 feet
Answers
Answer:
d
Step-by-step explanation:
use Pythagoras theorem
that is a²+b²=c²
so 4.5²+b²= 18²
rearrange to b²=18²-4.5²
so you get b=
\( \sqrt{303.75} \)
that is equal to 17.42842506
Related Questions
Find a vector equation and parametric equations for the line. (Use the parameter t.) The line through the point (1, 0, 6) and perpendicular to the plane x + 4y + z = 7 r(t): (1,0,6) + t(1,4,1) (x(t), y(t), z(t)) ) = (T)
Answers
The vector equation for the line is:
r(t) = (1, 0, 6) + t(-4, 1, 4)
The parametric equations for the line.
x(t) = 1 - 4t
y(t) = t
z(t) = 6 + 4t
To find a vector equation and parametric equations for the line passing through the point (1, 0, 6) and perpendicular to the plane x + 4y + z = 7, we can first determine the direction vector of the line.
The normal vector of the plane x + 4y + z = 7 is (1, 4, 1) since the coefficients of x, y, and z represent the normal vector.
Any line perpendicular to this plane must have a direction vector orthogonal to the normal vector of the plane.
Let's call the direction vector of our line (a, b, c).
We know that the dot product of the direction vector and the normal vector of the plane is zero:
(a, b, c) ⋅ (1, 4, 1) = 0
This equation gives us a condition for the direction vector.
We can choose any values for a, b, and c as long as they satisfy this condition.
For simplicity, we can choose a = -4, b = 1, and c = 4, which gives us a direction vector (-4, 1, 4) orthogonal to the plane.
Now, let's denote the position vector of the given point (1, 0, 6) as (x₀, y₀, z₀) = (1, 0, 6).
The vector equation of the line can be written as:
r(t) = r₀ + t × v
where r₀ is the position vector of a point on the line (which is (1, 0, 6)), t is the parameter, and v is the direction vector of the line (-4, 1, 4).
Therefore, the vector equation for the line is:
r(t) = (1, 0, 6) + t × (-4, 1, 4)
Expanding this equation, we get:
x(t) = 1 - 4t
y(t) = t
z(t) = 6 + 4t
These are the parametric equations for the line passing through the point (1, 0, 6) and perpendicular to the plane x + 4y + z = 7.
Learn more about vector equation and parametric equations click;
https://brainly.com/question/30550663
#SPJ4
maths functions question

Answers
Answer:
a) OA = 1 unit
b) BC = 3 units
c) OD = 2 units
d) AC = 3√2 units
Step-by-step explanation:
Given function:
\(f(x)=\dfrac{2}{x}-2\)
Part (a)Point A is the x-intercept of the curve.
To find the x-intercept of the curve (when y = 0), set the function to zero and solve for x:
\(\begin{aligned}f(x) & = 0\\\implies \dfrac{2}{x}-2 & = 0\\\dfrac{2}{x} & = 2\\2 & = 2x\\\implies x & = 1\end{aligned}\)
Therefore, A (1, 0) and so OA = 1 unit.
Part (b)If OB = 2 units then B (-2, 0). Therefore, the x-value of Point C is x = -2.
To find the y-value of Point C, substitute x = -2 into the function:
\(\implies f(-2)=\dfrac{2}{-2}-2=-3\)
Therefore, C (-2, -3) and so BC = 3 units.
Part (c)Asymptote: a line that the curve gets infinitely close to, but never touches.
The y-value of Point D is the horizontal asymptote of the function.
The function is undefined when x = 0 and therefore when y = -2.
Therefore, D (0, -2) and so OD = 2 units.
Part (d)From parts (a) and (c):
A = (1, 0)C = (-2, -3)To find the length of AC, use the distance between two points formula:
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
\(\textsf{where }(x_1,y_1) \textsf{ and }(x_2,y_2)\:\textsf{are the two points.}\)
Therefore:
\(\sf \implies AC=\sqrt{(x_C-x_A)^2+(y_C-y_A)^2}\)
\(\sf \implies AC=\sqrt{(-2-1)^2+(-3-0)^2}\)
\(\sf \implies AC=\sqrt{(-3)^2+(-3)^2}\)
\(\sf \implies AC=\sqrt{9+9}\)
\(\sf \implies AC=\sqrt{18}\)
\(\sf \implies AC=\sqrt{9 \cdot 2}\)
\(\sf \implies AC=\sqrt{9}\sqrt{2}\)
\(\sf \implies AC=3\sqrt{2}\:\:units\)

Find the height of a cylinder with a volume of 12157 mm3 and a radius of 9 mm.
Answers
Volume of a Cylinder = pi * r^2 * h
V / (pi*r^2) = h
12157 / (pi * 9^2) = h = 47.774
Can someone please explain how to do this? Not just the answer, please.

Answers
Answer:
Row n ---> 27th term is 27.
Row T ---> 27th term is 80.
Step-by-step explanation:
To find the 27th term for the top row, row n, you will use this formula:
an = a1 + f × (n-1)
The first number = 1
The common difference (f) = 1
a27 = 1 + 1 × (27-1)
a27 = 1 + 27 - 1
a27 = 28 - 1
a27 = 27
So, the 27th term is 27.
We will do the same for the row T.
an = a1 + f × (n-1)
The first number = 2
The common difference (f) = 3
a27 = 2 + 3 × (27-1)
a27 = 2 + 81 - 3
a27 = 83 - 3
a27 = 80
So, the 27th term is 80.
If mZ1 = 53° and mZ2 = 71°, find m24.
Answers
Answer:
53
Step-by-step explanation:
Given this A matrix A=
⎣
⎡
12
4
8
11
14
15
9
3
3
4
13
4
13
4
14
6
3
4
10
8
6
13
9
9
14
5
12
12
6
9
⎦
⎤
We wish to do the following a) F=A(2, odd )+A( even, 3)
∘
b) S=A([
1
3
],[
3
4
])
∘
÷A([
1
3
],[
3
4
]) Hint: Use element-wise division c) T=A(3,5)×A(4,3) Script 8
Answers
Performing operations on the given matrix,
a) F = [17, 12, 17, 23, 18, 17]
b) S = [[1, 1], [1, 1]]
c) T = 72
a) To calculate F, we need to perform two operations:
1. A(2, odd): This selects the elements from the 2nd row of matrix A at odd column indices.
A(2, odd) = [4, 8]
2. A(even, 3): This selects the elements from even rows of matrix A at the 3rd column index.
A(even, 3) = [13, 4, 4]
Now, we can perform element-wise addition between A(2, odd) and A(even, 3):
F = A(2, odd) + A(even, 3)
= [4, 8] + [13, 4, 4]
Since the dimensions do not match, we need to align the vectors by repeating the shorter one:
F = [4, 8] + [13, 4, 4] = [4, 8] + [13, 4, 4, 13, 4, 4] = [4+13, 8+4, 13+4, 10+13, 14+4, 13+4]
= [17, 12, 17, 23, 18, 17]
Therefore, F = [17, 12, 17, 23, 18, 17].
b) To calculate S, we need to perform element-wise division:
S = A([1, 3], [3, 4]) ÷ A([1, 3], [3, 4])
This means we select the elements from the 1st and 3rd rows, and from the 3rd and 4th columns of matrix A:
S = [[13, 8], [14, 6]] ÷ [[13, 8], [14, 6]]
Element-wise division simply divides corresponding elements from the two matrices:
S = [[13/13, 8/8], [14/14, 6/6]]
= [[1, 1], [1, 1]]
Therefore, S = [[1, 1], [1, 1]].
c) To calculate T, we need to multiply the element at position (3, 5) with the element at position (4, 3) in matrix A:
T = A(3, 5) × A(4, 3)
= 12 × 6
= 72
Therefore, T = 72.
To know more about matrix, refer here:
https://brainly.com/question/29132693
#SPJ4
Complete Question:
Given this A matrix
A = [[12 9 13 10 14] [ 4 3 4 8 5] [8 3 14 6 12] [11 4 6 13 12] [ 14 13 3 9 6] [15 4 4 9 9]]
We wish to do the following
a) F=A(2, odd )+A( even, 3)
b) S=A([ 1 3 ],[ 3 4 ]) ÷ A([ 1 3 ],[ 3 4 ]) Hint: Use element-wise division
c) T=A(3,5)×A(4,3)
4(-2x-7) use distributive property to expand it
Answers
Answer:
-8x-28 is after the distributive prop simplified
Step-by-step explanation:
4(-2x-7)
(4×-2x)-(4×-7)= -8x-28
HELP PLEASE!!!
Assume a class has 25 students.
a) If 80% of the class passed the test, how many students passed?
students
b) If 7 students got A’s on the test, what percent of students got A’s?
%
Answers
Answer:
A) 20
B) 28%
Step-by-step explanation:
A) In order to find percentages you need to make them in to decimals. 80% as a decimal is .8, if you multiply 25 by the decimal .8, you get 20.
B) To find the percentage all you do is divide, 7/25, this gives you the decimal .28, this as a percentage is 28%.
a 9-ft roll of wrapping paper costs $6.48, what is the price per inch?
Answers
Answer: $0.06 per inch
Concept:
When encountering questions that ask for unit price, follow the statements to get the answer. For example, this question asks the price per inch. Therefore, in the actual answer, use the total price given divided by the number of inches.
Solve:
Price = $6.48
Inch = 9 × 12 = 108 in
1 ft = 12 inchPrice / Inch = 6.48 / 108 = $0.06 per inch
Hope this helps!! :)
Please let me know if you have any questions
Josh has a part-time job mowing yards. On average, it takes him 2.25 hours to mow one yard. If he completed 6 1/3 yards this weekend, how many hours did he spend mowing yards
Answers
Answer:
14.25 hours
Step-by-step explanation:
We know
2.25 hours = 1 yard
13.5 hours = 6 yards
1/3 yard = 2.25 / 3 = 0.75 hours
To find how long it takes him to complete 6 1/3 yards, we take
13.5 + 0.75 = 14.25 hours
So, he spent 14.25 hours mowing yards.
What is the energy of each of the following photons in kilojoules per mole?a) ν= 5.92×1019 s−1b) ν= 1.24×106 s−1c) λ = 265 m
Answers
The energy of each photon is:
a) 239.3 kJ/mol
b) \(4.97 * 10^-4 kJ/mol\)
c) \(5.07 * 10^-4 kJ/mol\)
To calculate the energy of each photon in kilojoules per mole, we'll use the following equation:
E = h × ν × (Avogadro's number) / 1000
where E is the energy, h is Planck's constant (6.626 × 10^-34 Js), ν is the frequency in \(s^-1,\) and Avogadro's number is \(6.022 * 10^23 mol^-1.\)
For part c, we'll first convert the wavelength to frequency using the speed of light equation:
ν = c / λ
where c is the speed of light (3.00 × 10^8 m/s) and λ is the wavelength in meters.
a) ν = \(5.92 * 10^19 s^-1\)
E = \((6.626 * 10^-34 Js) * (5.92 * 10^19 s^-1) * (6.022 * 10^23 mol^-1) / 1000\)
E ≈ 239.3 kJ/mol
b) ν \(= 1.24 * 10^6 s^-1\)
E =\((6.626 * 10^-34 Js)\) * \((1.24 * 10^6 s^-1)\) * \((6.022 * 10^23 mol^-1) / 1000\)
E ≈ 4.97 × 10^-4 kJ/mol
c) λ = 265 m
ν =\((3.00 * 10^8 m/s) / (265 m)\)
ν ≈ 1.13 × 10^6 s^-1
E = \((6.626 * 10^-34 Js)\) *\((1.13 * 10^6 s^-1)\) * \((6.022 * 10^23 mol^-1) / 1000\)
E ≈ 5.07 × 10^-4 kJ/mol.
For similar question on energy.
https://brainly.com/question/22236101
#SPJ11
(b-3)squared expanded
Answers
Answer:
Step-by-step explanation:
(x - y)² = x² - 2xy + y²
x = b ; y = 3
(b - 3)² = b² - 2 *b * 3 + 3²
= b² - 6b + 9
A recipe calls for 3 avocados for each bowl of guacamole. How many full bowls of guacamole can be made with 17 avocados?
Answers
Answer:
5 full bowls
Step-by-step explanation:
Set up a proportion where x is the number of bowls with 17 avocados:
\(\frac{3}{1}\) = \(\frac{17}{x}\)
Cross multiply and solve for x:
3x = 17
x = 5.67
This means that 5 full bowls of guacamole can be made with 17 avocados.
Answer: 5 full bowl
Step-by-step explanation:
17 divided by 3 = 5 full bowls 2 avocados
For the triangles to be similar to be similar be the similarity theorem, what must be the value of y?
Answers
Without further details or measurements, it is not possible to determine the exact value of y that would satisfy the similarity theorem for triangles to be similar.
In order for triangles to be similar by the similarity theorem, the value of y must satisfy the condition of proportional sides. The similarity theorem states that if two triangles have their corresponding angles equal and their corresponding sides in proportion, then the triangles are similar.
Let's consider two triangles, Triangle ABC and Triangle DEF, where the corresponding sides are AB and DE, BC and EF, and AC and DF. If we want these triangles to be similar, then the ratio of the lengths of corresponding sides must be equal.
For example, if we want the ratio of AB to DE to be equal to the ratio of BC to EF, we have AB/DE = BC/EF. Similarly, for the other pairs of corresponding sides, we have AB/DE = AC/DF and BC/EF = AC/DF.
To find the value of y, we need to set up an equation based on the given information. However, without any specific information or measurements for the triangles, it is not possible to determine the exact value of y. The value of y will depend on the specific lengths of the sides of the triangles and the ratios they form.
for more such question on measurements
https://brainly.com/question/27233632
#SPJ8
I'm stuck on like 3 I'm in fourth help plss
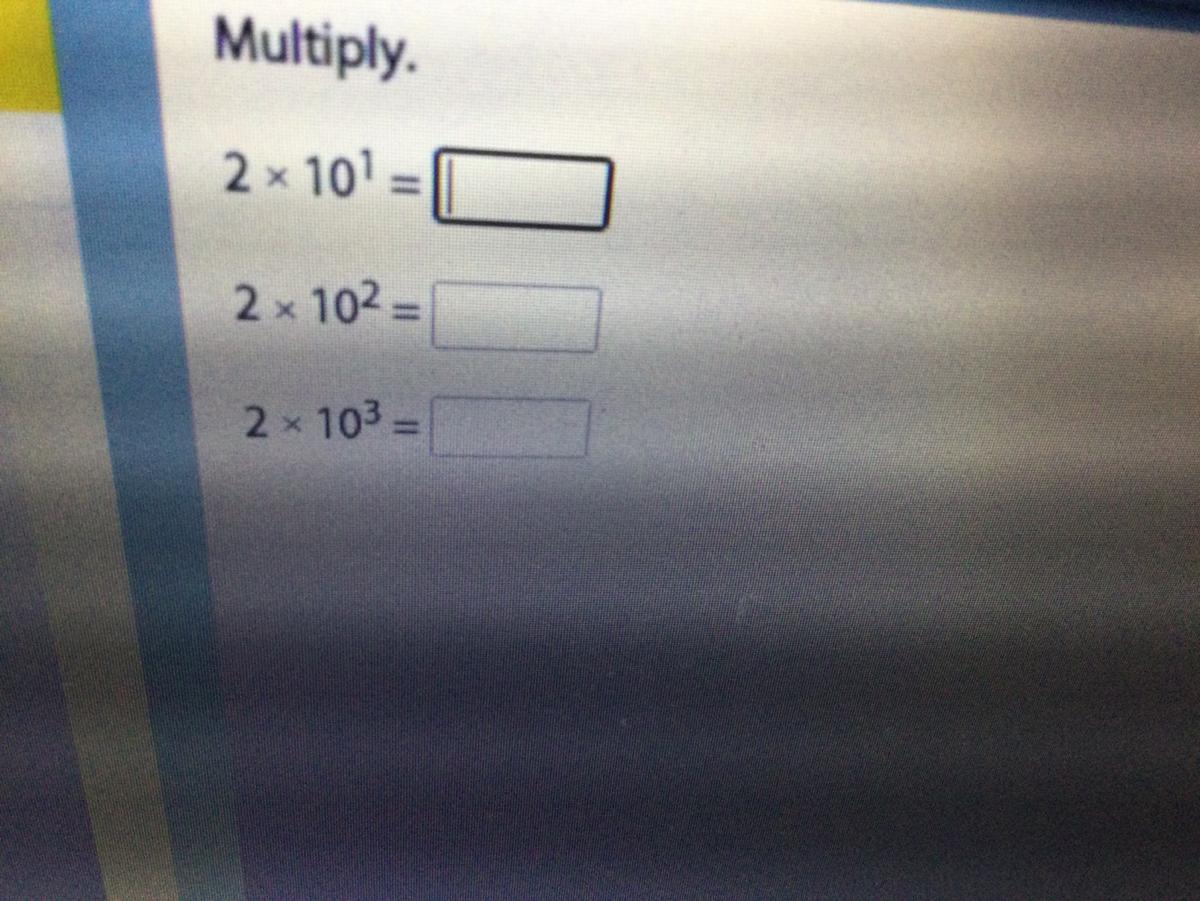
Answers
Answer:
I got you buddy!
1. 20
2. 200
3. 2000
Step-by-step explanation:
So when you see a number with a little number you multiply the number by itself the same amount of times as the little number up top for example.
10x1= 10
10x10=100
10x10x10=1000
then what you do is take those numbers we multiplied and multiply them again by 2
so its.
2x10=20
2x100=200
2x1000=2000
Hope this helped you buddy!
A random variable X has a probability distribution as follows:
X = 0, 1, 2, 3
P(X) = 2k, 3k, 13k, 2k
where k is a positive constant. What is the probability P(X < 2.0)?
a. 0.90
b. 0.25
c. 0.65
d. 0.15
e. 1.00
Answers
A random variable X has a probability distribution as follows:
X = 0, 1, 2, 3
P(X) = 2k, 3k, 13k, 2k
where k is a positive constant. The probability P(X < 2.0) is 0.25.
What is random variable?
A quantity or item that depends on random events is formalised mathematically as a random variable, also known as a random quantity, aleatory variable, or stochastic variable. It is a function or mapping from potential outcomes to a quantifiable space, frequently to real numbers.
We know that probability sum of all events is 1
Therefore here sum of all probability events =P(X=0)+P(X=1)+P(X=2)+PX=3)=1
2k+3k+13k+2k=1
20k=1
k=1/20=0.05
For P(x<2)=P(X=0)+P(X=1)=2k+3k =5k=5*(1/20)=0.25
Hence the correct answer is b, 0.25
To learn more about random variable from the given link
https://brainly.com/question/17217746
#SPJ1
Question:
Cube A has a volume of 128 cm. If the edge lengths of cube B are half the size of the edge lengths of cube A, what is the volume of cube B?
cube A
cube B
V = 128 cm
V = ?
o 16 cm3
O 64 cm3
O 32 cm
Cannot be determined
Answers
Answer:
16 cm3
Step-by-step explanation:
4 x 4 x 8 = 128
2 x 2 x 4 = 16
Answer:16 cm
Step-by-step explanation:
Simplify an expression for the perimeter of the
rectangle shown.

Answers
Answer:
17.2x + 16.4
Step-by-step explanation:
→ Perimeter = All sides added together
8.6x + 3 + 8.6x + 3 + 5.2 + 5.2
→ Simplify
17.2x + 6 + 10.4
→ Simplify further
17.2x + 16.4
How much would $100 invested at 6% interest compounded monthly be worth after 20 years ? Round your answer to the nearest cent
Answers
Answer:
$331.02
Step-by-step explanation:
the fifth term of the sequence is 5 and the sixth term is 2.5. What is the 2nd term?
Answers
Answer:
Let's denote the first term of the sequence as a, and the common difference between consecutive terms as d.
Then, we know that the fifth term is 5, so:
a + 4d = 5
Similarly, we know that the sixth term is 2.5, so:
a + 5d = 2.5
We can solve this system of equations by subtracting the first equation from the second:
(a + 5d) - (a + 4d) = 2.5 - 5
d = -2.5
Now, we can substitute this value of d into either equation to find the value of a:
a + 4d = 5
a + 4(-2.5) = 5
a - 10 = 5
a = 15
Therefore, the first term of the sequence is 15, and the common difference is -2.5. We can use this to find the value of the second term:
a + d = 15 + (-2.5) = 12.5
Therefore, the second term of the sequence is 12.5.
mark my answer as brainliest
prove that 5^(2n - 1) is divisible by 8
Answers
Your teacher must have made a typo somewhere. The expression 5^(2n-1) is not divisible by 8.
The expression 5^(2n-1) is composed of 2n-1 copies of "5" multiplied together. The key here is that 5 is the only unique prime factor of this number.
On the other hand, 8 = 2*2*2 = 2^3 showing that 2 is the only prime factor for this number. At this point, we can see that there's no way that 5^(2n-1) is divisible by 8. It all comes down to the clash of the primes 5 and 2 not matching up, and having nothing in common.
Let's consider a few concrete examples:
If n = 1, then 5^(2n-1) = 5^(2*1-1) = 5^1 = 5 which is not divisible by 8. The number 5/8 = 0.625 isn't an integer.If n = 2, then 5^(2n-1) = 5^(2*2-1) = 5^3 = 125 which is also not a multiple of 8. The number 125/8 = 15.625 isn't an integer.I'll let you try other natural numbers for n, and you'll find that \(\frac{5^{2n-1}}{8}\) isn't an integer.
I need Geometry Tutor onna low but can anyone figure this out ?

Answers
Answer: angle 1 = 22 degrees
============================================
Work Shown:
x = measure of angle 1 = unknown
y = measure of angle 2 = 49
x+y = measure of angle PQS = 71
x+y = 71
x+49 = 71
x+49-49 = 71-49 .... subtract 49 from both sides
x = 22
angle 1 is 22 degrees.
Answer:
\(m \angle 1\) = 49º.
Step-by-step explanation:
We are given that \(m\angle PQS\) is 71º and \(m \angle 2\) is 49º. Since \(m \angle 1 + m \angle 2\) must equal \(m\angle PQS\), we have that 49º + \(m \angle 1\) = 71º. Therefore, \(m \angle 1\) = 71º - 49º = 22º.
Derivations (20 marks): For each of the questions in this section provide a derivation. Other methods will receive no credit i. ∃x(Fx & Gx) ⊢ ∃xFx & ∃xGx (5 marks)
ii. ¬ 3x(Px v Qx) ⊢ Vx ¬ Px (5 marks) iii. ¬ Vx(Fx → Gx) v 3xFx (10 marks; Hint: To derive this theorem use RA.)
Answers
¬ Vx(Fx → Gx) v 3xFx ⊢ Fx → Gx [1-5, Modus Ponens]
i. ∃x(Fx & Gx) ⊢ ∃xFx & ∃xGx (5 marks)
Proof:
1. ∃x(Fx & Gx) [Premise]
2. Fx & Gx [∃-Elimination, 1]
3. ∃xFx [∃-Introduction, 2]
4. ∃xGx [∃-Introduction, 2]
5. ∃xFx & ∃xGx [Conjunction Introduction, 3 and 4]
6. ∃x(Fx & Gx) ⊢ ∃xFx & ∃xGx [1-5, Modus Ponens]
ii. ¬ 3x(Px v Qx) ⊢ Vx ¬ Px (5 marks)
Proof:
1. ¬ 3x(Px v Qx) [Premise]
2. ¬ Px v ¬ Qx [DeMorgan’s Law, 1]
3. Vx ¬ Px [∀-Introduction, 2]
4. ¬ 3x(Px v Qx) ⊢ Vx ¬ Px [1-3, Modus Ponens]
iii. ¬ Vx(Fx → Gx) v 3xFx (10 marks; Hint: To derive this theorem use RA.)
Proof:
1. ¬ Vx(Fx → Gx) v 3xFx [Premise]
2. (¬ Vx(Fx → Gx) v 3xFx) → (¬ Vx(Fx → Gx) v Fx) [Implication Introduction]
3. ¬ Vx(Fx → Gx) v Fx [Resolution, 1, 2]
4. (¬ Vx(Fx → Gx) v Fx) → (Fx → Gx) [Implication Introduction]
5. Fx → Gx [Resolution, 3, 4]
6. ¬ Vx(Fx → Gx) v 3xFx ⊢ Fx → Gx [1-5, Modus Ponens]
Learn more about Derivations
brainly.com/question/30365299
#SPJ11
SECTION A (20 MARKS) QUESTION 1 (a)Identify the relevant population for the below foci, and suggest the appropriate sampling design to investigate the issues, explaining why they are appropriate. Wherever necessary identify the sampling frame as well. 10 marks A public relations research department wants to investigate the initial reactions of heavy soft- drink users to a new all-natural soft drink'. (b) What type of sampling design is cluster sampling? What are the advantages and disadvantages of cluster sampling? Describe a situation where you would consider the use of cluster sampling. 10 marks
Answers
a) The relevant population is the heavy soft-drink users in the given case, and the appropriate sampling design that should be used is stratified random sampling. The list of all heavy soft-drink users is the sampling frame.
b) Cluster sampling refers to a sampling design where population is divided into naturally occurring groups and a random sample of clusters is chosen.
The advantages are efficient, easy to perform, and used when the population is widely dispersed. The disadvantages are sampling errors, have lower level of precision, and have the standard error of the estimate.
a) The relevant population for the public relations research department to investigate the initial reactions of heavy soft-drink users to a new all-natural soft drink is heavy soft-drink users. The appropriate sampling design that can be used to investigate the issues is stratified random sampling.
Stratified random sampling is a technique of sampling in which the entire population is divided into subgroups (or strata) based on a particular characteristic that the population shares. Then, simple random sampling is done from each stratum. Stratified random sampling is appropriate because it ensures that every member of the population has an equal chance of being selected.
Moreover, it ensures that every subgroup of the population is adequately represented, and reliable estimates can be made concerning the entire population. The list of all heavy soft-drink users can be the sampling frame.
b) Cluster sampling is a type of sampling design in which the population is divided into naturally occurring groups or clusters, and a random sample of clusters is chosen. The elements within each chosen cluster are then sampled.
The advantages of cluster sampling are:
Cluster sampling is an efficient method of sampling large populations. It is much cheaper than other types of sampling methods.Cluster sampling is relatively easy to perform compared to other methods of sampling, such as simple random sampling.Cluster sampling can be used when the population is widely dispersed, and it would be difficult to cover the entire population.The disadvantages of cluster sampling are:
Cluster sampling introduces sampling errors that could lead to biased results.Cluster sampling has a lower level of precision and accuracy compared to other types of sampling methods.Cluster sampling increases the standard error of the estimate, making it difficult to achieve the desired level of statistical significance.A situation where cluster sampling would be appropriate is in investigating the effects of a new medication on various groups of people. In this case, the population can be divided into different clinics, and a random sample of clinics can be selected. Then, all patients who meet the inclusion criteria from the selected clinics can be recruited for the study. This way, the study will be less expensive, and it will ensure that the sample is representative of the entire population.
Learn more about Stratified random sampling:
https://brainly.com/question/20544692
#SPJ11
whitch is the decimal equivalent to 17/20
Answers
Answer:
0.85
Step-by-step explanation:
I just need 20 characters
Answer: .85
Step-by-step explanation:
Nathan is 1.25 meters tall. At 1 p.m., he measures the length of a tree's shadow to be
24.65 meters. He stands 20.1 meters away from the tree, so that the tip of his shadow
meets the tip of the tree's shadow. Find the height of the tree to the nearest
hundredth of a meter.

Answers
The height of the tree is 6.77 meters.
What are similar triangles?Triangles with the same shape but different sizes are said to be similar triangles. Squares with any side length and all equilateral triangles are examples of related objects. In other words, if two triangles are identical, their respective sides are equal in number and their corresponding angles are congruent.
Given that, the height of the person is 1.25 meters, the length of the tree's shadow is 24.65 meters, and the distance between the person and the tree is 20.1 meters.
Let the height of the tree be x.
Note that the scenario makes two similar triangles.
Since the ratio of the side lengths of similar triangles is proportional, it follows:
(24.65 - 20.1)/1.25 = 24.65/x
3.64 = 24.65/x
x = 24.65 / 3.64
x = 6.77
Hence, the height of the tree is 6.77 meters.
Learn more about similar triangles here:
https://brainly.com/question/24173643
#SPJ1
please answer for those with step by step
v^3 = 36
c^2 = 4
Answers
6c^2=4,\:v^3 so yeah that is it
Now let's do linear regression to use Alcohol Content to predict Calories. What is the population model we are estimating? (choose from the options below) a. AlcoholContent =β0+β1 Calories +ϵ b. Calories =β0+β1 AlcoholContent +ϵ c. Calories =β0+β1 AlcoholContent +ϵ d. AlcoholContent =β0+β1 Calories +ϵ e. AlcoholContent =b0+b1 Calories
Answers
Answer:
d. AlcoholContent =β0+β1 Calories +ϵ
Step-by-step explanation:
The population model would be the equation that models the relationship between two variables, in this case AlcoholContent and Calories. Since the objective is to use Alcohol Content to predict Calories, the population model we are estimating should be d. AlcoholContent =β0+β1 Calories +ϵ.
The population model we are estimating in this scenario is option d: AlcoholContent = β0 + β1 Calories + ϵ. In linear regression, we aim to estimate the relationship between two variables by fitting a line to the data points.
The population model represents the true underlying relationship between the predictor variable (AlcoholContent) and the response variable (Calories).
In this case, the equation AlcoholContent = β0 + β1 Calories + ϵ suggests that the AlcoholContent is the dependent variable, and it is being predicted based on the independent variable Calories. The β0 and β1 coefficients represent the intercept and slope of the regression line, respectively. The ϵ term represents the error or residual term, which captures the variability in the data that is not accounted for by the regression model.
So, the population model we are estimating is AlcoholContent = β0 + β1 Calories + ϵ, where β0 and β1 are the coefficients to be estimated.
Learn more about population here: https://brainly.com/question/30935898
#SPJ11
(1) A pizza restaurant had 3/5 of a gallon of pizza sauce left at the end of the evening and
divided it equally among 6 pizzas. How much sauce did they put on each pizza?
Answers
Answer:
The pizza restaurant put 1/10 of the sauce on each pizza.
Step-by-step explanation:
Take the 3/5, and on a calculator divide the 3 by the 5:
0.6
Then, take the 0.6 and divide it by the 6 pizzas:
0.1, converted into a fraction equals 1/10.
The pizza restaurant put 1/10 of the sauce on each pizza.
May I have Brainliest please? My next rank will be the highest one: A GENIUS! Please help me on this journey to become top of the ranks! I only need 10 more brainliest to become a genius! I would really appreciate it, and it would make my day! Thank you so much, and have a wonderful rest of your day!
PELASE HELP MEEEEE I REALLY NEED HELP

Answers
Answer:
2. 7238.23 mm
3. 55.42 ft
4. 703.86 ft
Step-by-step explanation:
Answer:
1. 7234.56mm^2 2. 55.39ft^2 3. 706.5ft^2