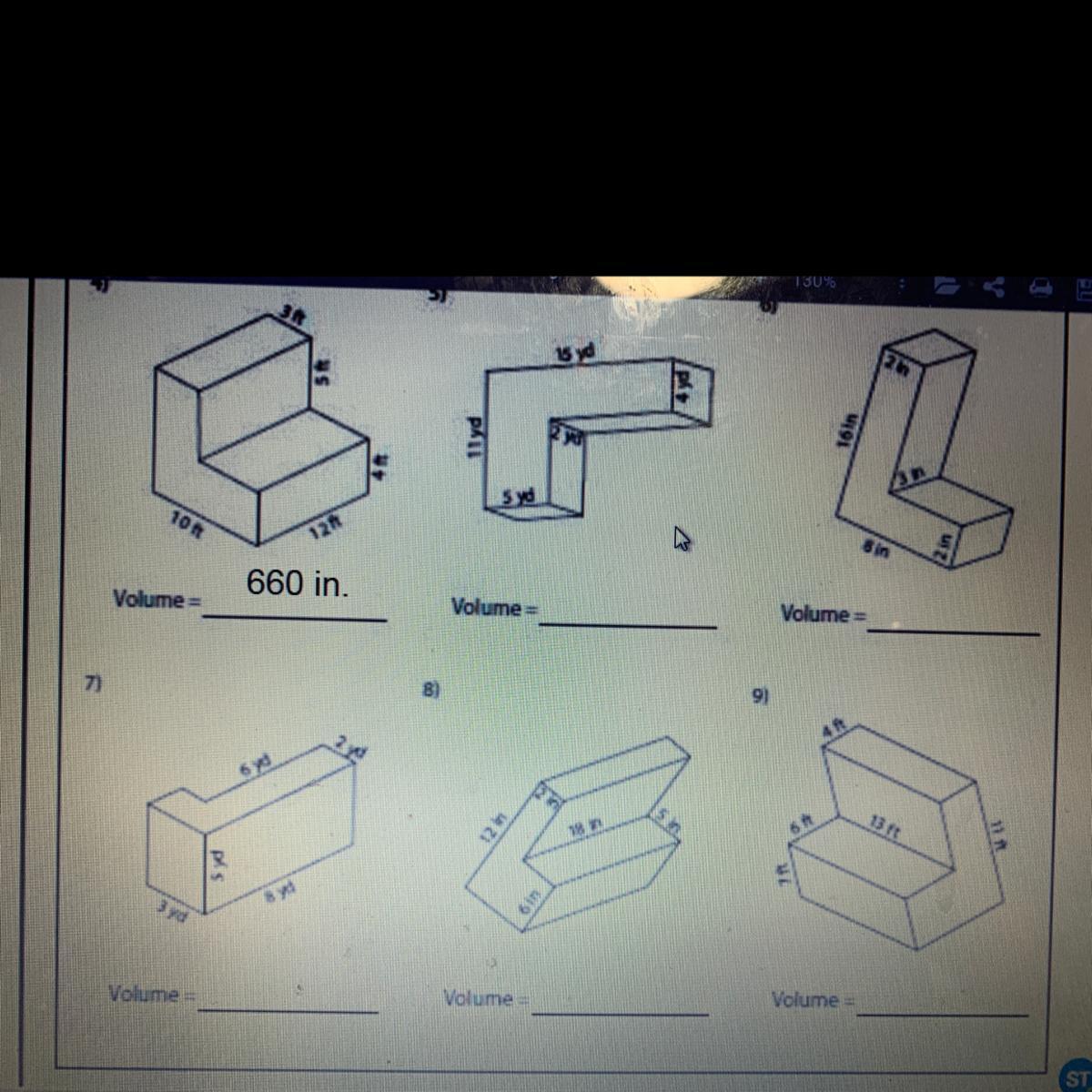
Answers
Answer/Step-by-step explanation:
Decompose each shape, find the volume of each cuboid, and add both volumes you get together.
Recall: volume of cuboid = L*W*H
4. Volume of cuboid 1: L*W*H = 12*10*4 = 480 ft³
Volume of cuboid 2: L*W*H = 12*3*5 = 180 ft³
Volume of the shape = 480 + 180 = 660 in.³
5. Volume of cuboid 1: L*W*H = 11*2*5 = 110 yd³
Volume of cuboid 2: L*W*H = 10*4*2 = 80 yd³
Volume of the shape = 110 + 80 = 190 yd³
6. Volume of cuboid 1: L*W*H = 8*3*2 = 48 in.³
Volume of cuboid 2: L*W*H = 14*2*3 = 84 in.³
Volume of the shape = 48 + 84 = 132 in.³
7. Volume of cuboid 1: L*W*H = 5*3*2 = 30 yd³
Volume of cuboid 2: L*W*H = 6*2*5 = 60 yd³
Volume of the shape = 30 + 60 = 90 yd³
8. Volume of cuboid 1: L*W*H = 12*2*18 = 432 in.³
Volume of cuboid 2: L*W*H = 18*5*6 = 540 in.³
Volume of the shape = 432 + 540 = 972 in.³
9. Volume of cuboid 1: L*W*H = 13*11*4 = 572 ft³
Volume of cuboid 2: L*W*H = 13*6*7 = 546 ft³
Volume of the shape = 572 + 546 = 1,118 ft³
Related Questions
The radius of a circle is 11ft. Find its area in terms of pi
Answers
Answer: A≈380.13ft²
Step-by-step explanation:
The sum of 2 numbers s 1 and the diffreance is 5 what are th 2 numbers
Answers
Answer:
note ;sum of two no. is not 1.
let no. be x and y.
we have
x+y=11.......(1)
x-y=5........(2)
adding equation 1&2
x+y+x-y=11+5
2x=16
x=16/2=8
again
8-y=5
y=8-5=3
:.
x=8,y=3
\( \frac{1}{6} (x + 12) = - 4\)Can you please solve it
Answers
Problem
\( \frac{1}{6} (x + 12) = - 4\)
Solution
For this case we have the following equation given:
\(\frac{1}{6}(x+12)=-4\)We can multiply both sides by 6 and we got:
\(x+12=-24\)Now we can subtract 12 in both sides and we got:
\(x=-24-12=-36\)And the solution for this case would be x=-36
You can use the equation A =(HW/3600)^1/2
to approximate a person's body surface area A (in square meters), where H
is height (in centimeters) and W is weight (in kilograms). Approximate the body surface area of a person with a height
of 160 centimeters and a weight of 64 kilograms.
Body surface area:______
m²
Answers
The body surface area is given by the equation A = 1.6865 m²
What is an Equation?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the body surface area be represented as A
Now , the equation will be
A = ( HW / 3600 )^1/2
A = √( HW / 3600 ) be equation (1)
where H is the height in centimeters and W is the weight in kilograms
Now , the value of H = 160 cm
The value of W = 64 kg
Substituting the values in the equation , we get
A = √ [ ( 160 x 64 ) / 3600 ]
On simplifying the equation , we get
A = √ ( 10240/3600 )
A = √ ( 2.8444 )
A = 1.6865 m²
Therefore , the body surface area is 1.6865 m²
Hence , the equation is A = 1.6865 m²
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
Sera had the number 548.She adds one to the tens and two to the units. What number would Sera end up with??
Answers
The number she'd have is:
560Explanation:
First, let's see which number is in the tens place and which number is in the ones place (the units place).
In the number 548, the place value of 5 is hundreds, the place value of 4 is tens, and the place value of 8 is ones (or units).
So if Sera adds two to the units, she'll have 10. But, since we can't write the number as 5410 (that would be a totally different number), we just write 0 in the units place, and shift 1 to the tens place, which gives us :
550
That's not all, since we also add 1 to the tens:
560
Hence, Sera ends up with 560.Explain the process you would use to find the area of the shaded region. Then calculate the shaded region.
You may leave your answer in terms of π or round to the nearest tenth.

Answers
The shaded region of the rectangle is 242.9 cm² and the shaded region of the sector is 7.1 square units.
What is the area of the shaded regions?Question 17) is a figure of a rectangle and two inscribed circles.
The area of a rectangle is expressed as: A = length × width
The area of a circle is expressed as: A = πr²
Where r is the radius.
To determine the area of the shaded region, we simply subtract the areas of the two circles from the area of the rectangle.
Area = ( Length × width ) - 2( πr² )
Area = ( 40 × 10 ) - 2( π × 5² )
Area = ( 400 ) - 2( 25π )
Area = 400- 50π
Area = 242.9 cm²
Area of the shaded region is 242.9 squared centimeters.
Question 18) is the a figure a sector of a circle and a right triangle.
The area of a sector is expressed as: A = (θ/360º) × πr²
The area of a triangle is expressed as: A = 1/2 × base × height
To determine the area of the shaded region, we simply subtract the areas of the triangle from the area of the sector.
Hence:
Area = ( (θ/360º) × πr² ) - ( 1/2 × base × height )
Plug in the values:
Area = ( (90/360º) × π × 5² ) - ( 1/2 × 5 × 5 )
Area = 25π/4 - 12.5
Area = 7.1
Therefore, the area of the shaded region is 7.1 square units.
Learn more about circles here: brainly.com/question/11952845
#SPJ1
Please help me !! I need help asap

Answers
In given fractions 8/9 is 1/36 large than 31/36
Comparing Fractions:Finding the larger and smallest fraction in between two or more fractions is known as comparing fractions.
We need to change fractions with unlike denominators into fractions with similar denominators in order to compare them. For this, we will find the denominators' Least Common Multiple (LCM).
If the denominators are the same then it is easy to compare the fractions.
Here we have
31/36 and 8/9
To find the largest fraction convert both denominators into the same
Here LCM(36, 9) = 36
Now multiply both numerator and denominators of fractions with a number to change the denominators
=> \(\frac{31}{36} \times \frac{1}{1} = \frac{31}{36}\)
=> \(\frac{8}{9} \times \frac{4}{4} = \frac{32}{36}\)
From the above calculations given fractions are 31/36 and 32/36
Difference = \(\frac{32}{36} - \frac{31}{36} = \frac{1}{36}\)
Therefore,
In given fractions 8/9 is 1/36 large than 31/36
Learn more about Fractions at
https://brainly.com/question/14503941
#SPJ1
52 over 100 simplified
Answers
Answer:13/25
both 52 and 100 can be divided by 4
Step-by-step explanation:
Answer:
The simplest form of 52/100 is 13/25
Steps to simplifying fractions
Find the GCD (or HCF) of numerator and denominator
GCD of 52 and 100 is 4
Divide both the numerator and denominator by the GCD
52 ÷ 4
100 ÷ 4
Reduced fraction:
13
25
Therefore, 52/100 simplified to lowest terms is 13/25.
Step-by-step explanation:
Hope it helps!
Write an equation in general form (Ax+By+C =0) for the line that passes through A(2, 4) and B(11, 8).
Answers
Answer:
4x - 9y + 28 = 0------------------------
Find the slope of AB:
m(AB) = (8 - 4)/(11 - 2) = 4/9Use point-slope form and point A(2, 4) to determine the line:
y - 4 = (4/9)(x - 2)Multiply both sides by 9 to clear fraction:
9(y - 4) = 4(x - 2)Open parenthesis and convert the equation into ax + by + c = 0:
9y - 36 = 4x - 8 ⇒4x - 9y - 8 + 36 = 0 ⇒4x - 9y + 28 = 0Find the sum of the first 20 terms of the arithmetic sequence: (Use image below)

Answers
Cookies are sold in singly or in packages of 6 or 18. With this packaging how many ways can you buy 36 cookies?
Answers
The ways to pack are
10 singles. One package of 6 and 4 singles. One package of 6 and one packages of 4 Two packages of 4 and 2 singles One package of 4 and 6 singlesThis is further explained below.
What is packaging ?Generally, The science, art, and technology of packaging involves confining or safeguarding goods for distribution, storage, sale, and usage. The process of creating, analyzing, and designing packages is sometimes referred to as packaging.
In conclusion,
10 singles. One package of 6 and 4 singles. One package of 6 and one packages of 4 Two packages of 4 and 2 singles One package of 4 and 6 singlesRead more about packaging
https://brainly.com/question/12003033
#SPJ1
Help me out here pleaseeeeeeeeeeeee

Answers
Answer:
5 1/4
Step-by-step explanation:
7 days = 1 week, so 3/4 x 7 = 5 1/4
what is the absolute value of -4.5
Answers
Answer:4.5
Step-by-step explanation:
Answer:
Absolute value means any value but always positive. So |-4.5|=4.5
Find the slope of the line
A. -4
B. -1/4
C. 1/4
D. 4

Answers
Answer:
C. 1/4
hopes this helped
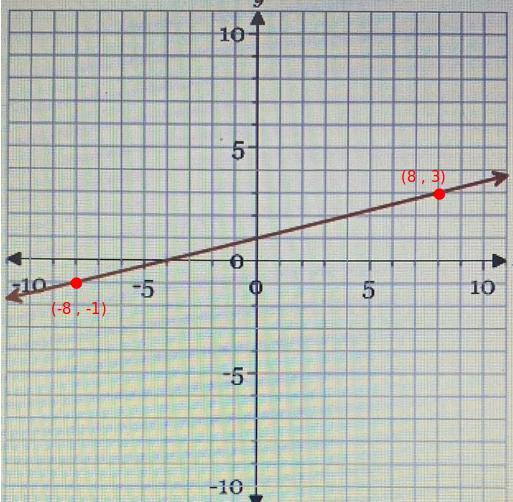
to get the equation of any straight line, we simply need two points off of it, let's use those two in the picture below
\((\stackrel{x_1}{-8}~,~\stackrel{y_1}{-1})\qquad (\stackrel{x_2}{8}~,~\stackrel{y_2}{3}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{3}-\stackrel{y1}{(-1)}}}{\underset{\textit{\large run}} {\underset{x_2}{8}-\underset{x_1}{(-8)}}} \implies \cfrac{3 +1}{8 +8} \implies \cfrac{ 4 }{ 16 } \implies \cfrac{1 }{ 4 }\)
In a board game, the distance a player travels is equal to the sum of the numbers shown when two 6-sided dice are tossed
How many different distances are possible?
Enter your answer as a number, like this: 42
Answers
The required number of different distances possible is given as 36.
Given that,
In a board game, the distance a player travels is equal to the sum of the numbers shown when two 6-sided dice are tossed.
In arithmetic, combination and permutation are two different ways of grouping elements of a set into subsets. In combination, the components of the subset can be recorded in any order. In a permutation, the components of the subset are listed in a distinctive order.
Here,
1 dice have 6 outcomes
2 dice have 6 outcomes,
Number of possible combination = 6 × 6 = 36
Thus, the required number of different distances possible is given as 36.
Learn more about permutations and combinations here:
https://brainly.com/question/2295036
#SPJ5
Find an equation of the line described below. Write the equation in slope intercept form( solved for y) when possible through (8,5) and (5,8)
Answers
\((\stackrel{x_1}{8}~,~\stackrel{y_1}{5})\qquad (\stackrel{x_2}{5}~,~\stackrel{y_2}{8}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{5}}}{\underset{\textit{\large run}} {\underset{x_2}{5}-\underset{x_1}{8}}} \implies \cfrac{ 3 }{ -3 } \implies - 1\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{5}=\stackrel{m}{- 1}(x-\stackrel{x_1}{8}) \\\\\\ y-5=-x+8\implies {\Large \begin{array}{llll} y=-x+13 \end{array}}\)
Hannah runs down the street to catch her bus. She runs for a total of 12 seconds. On the sidewalk, she runs 16 feet per second. When she crosses the street, she runs 3 feet per second. Hannah runs a total distance of 127 feet.
How many seconds did Hannah spend running on the sidewalk? Enter your answer in the box.
Answers
Answer:
7 seconds that Hannah runs on the side walk
Step-by-step explanation:
let's A is the second that Hannah runs on the side walk.
and B is the second that Hannah runss on the cross street. Base on the information we have 2 equations for 2 unknowns .
A + B = 12
16 A + 3 B = 127 simply to add/subtract column we have
=> 16A + 3B = 127 (1)
3A + 3B = 36 (2) runs on the side walk.
And 12-7 =5 seconds is the time that Hannah runs on the cross street.
Hannah spend 7 seconds for running on the sidewalk.
Here,
Hannah runs down the street to catch her bus.
She runs for a total of 12 seconds.
On the sidewalk, she runs 16 feet per second. When she crosses the street, she runs 3 feet per second.
Hannah runs a total distance of 127 feet.
We have to find, How many seconds did Hannah spend running on the sidewalk.
What is Linear equation in two variables?
Linear equations in two variables is defined as, If a, b, and r are real numbers then ax + by = r is called a linear equations in two variables.
Now,
Let X is the second that Hannah spend running on the sidewalk.
And, Y is the second that Hannah runes on the cross the street.
Since, She runs for a total of 12 seconds.
⇒ X + Y = 12 .... (i)
And, On the sidewalk, she runs 16 feet per second. When she crosses the street, she runs 3 feet per second and Hannah runs a total distance of 127 feet.
⇒ 16 X + 3 Y = 127 ....(ii)
By solving equation (i) and (ii), we get;
⇒ X = 7 and Y = 5
Hence, Hannah spend 7 seconds for running on the sidewalk.
Learn more about the Linear equation visit:
https://brainly.in/question/17407303
#SPJ2
What equation does this set of algebra tiles represent?
x
1
1
1
1
1
1
1
1
=
1
1
1
1
1
1
1
1
1
1
1
1
Combine like terms on each side of the equation. For example, write 3 instead of 1 + 1 + 1.
Answers
The equation of the set of algebra tiles is x + 8 = 12.
What are algebra tiles?Algebra tiles are mathematical manipulatives that help students comprehend the principles of algebra and strategies to think algebraically. For introductory algebra pupils at the level of elementary school, middle school, high school, and college, these tiles have been demonstrated to offer solid examples.
Given set,
x 1 1 1 1 1 1 1 1 = 1 1 1 1 1 1 1 1 1 1 1 1
the set has one positive x and eight positive units,
the equation is x + 8.
and on the right side of the equation, there are 12 positive units,
equation is x + 8 = 12
Hence the equation s x + 8 = 12.
Learn more about algebra tiles;
https://brainly.com/question/19447945
#SPJ1
Answer:
x + 8 = 12.
Step-by-step explanation:
in case you need it (x=4)
HELP ME PLEASE THANKS

Answers
Answer: Answer choice B
Step-by-step explanation:
move the dot -(-E) on the number line. E=3.5

Answers
write the following ratio as a fraction in lowest terms
5/3to7/6
Answers
10/7
hope it helps...!!!

what is the 12
th term rule of the linear sequence 13 7 1 -5 -11
Answers
Answer:
-53, f(n) = -6(n-1) + 13
Step-by-step explanation:
given the equation to this linear/arithmetic sequence for the nth term: f(n) = -6(n-1) + 13
f(12) = -6(12-1) + 13
f(12) = -6(11) + 13
f(12) = -66 + 13
f(12) = -53
*substitute and simplify*
______________
f(n) = f(1) + d(n-1)
given f(1) = 13, f(2) = 7, and f(3) = 1
7-13 = 1-7 = -6 = d
= f(1) + d(n-1)
f(1) = 13 so
the equation must be f(n) = 13 - 6(n-1) or -6(n-1) + 13
Convert 376 centimeters into meters ??
Answers
Answer: 3.76 meters
Step-by-step explanation:
Answer:
3.76
Step-by-step explanation:
Simplify the equation
4(5y – 5) =
Answers
Answer:
20y - 20
Step-by-step explanation:
We multiply the first term and the second term in the parentheses by the 4. That means we do:
4(5y) + 4(-5)
And we simplify to get:
20y - 20
2x-3\(\geq\) 0
Answers
Answer:
x ≥ 1.5
Step-by-step explanation:
2x - 3 ≥ 0 ( add 3 to both sides )
2x ≥ 3 ( divide both sides by 2 )
x ≥ 1.5
Boris started on the treadmill after setting timer for 99 minutes. The display says he have finished 43% of his run. How many minutes have gone by. Round to the nearest tenth
Answers
99 minutes * 0.43 = 42.57 minutes
Rounding to the nearest tenth, we can say that approximately 42.6 minutes have gone by.
The weight of an organ in adult males has a bell-shaped distribution with a mean of 310 grams and a standard deviation of 40 grams. Use the empirical rule to determine the following.
a. About 95 % of organs will be between what weights?
b. What percentage of organs weighs between 270 grams and 350 grams?
c. What percentage of organs weighs less than 270 grams or more than 350 grams?
d. What percentage of organs weighs between 230 grams and 430 grams?
Answers
Answer:
Step-by-step explanation:
Given that:
The mean μ = 310
The standard deviation σ = 40
Using the empirical rule to determine the following :
a. About 95 % of organs will be between what weights?
At 95% data values lies within 2 standard deviations of mean.
Thus, the required range is :
= μ ± 2σ
= ( 310 - 2 (40) , 310 + 2(40) )
= (230, 390)
b. What percentage of organs weighs between 270 grams and 350 grams
Here:
μ ± σ = (310 - 40, 310 + 40)
μ ± σ = (270, 350)
Using empirical rule, 68% data values is in the range within 1 standard deviation of mean. This implies that 68% data values lie between (270, 350).
c. What percentage of organs weighs less than 270 grams or more than 350 grams?
The complement theorem can be use to estimate the percentage of organs that weighs less than 270 grams or more than 350 grams,
This can be illustrated as :
= 100 % - 68 %
= 32 %
d. What percentage of organs weighs between 230 grams and 430 grams?
Using the empirical rule:
The percentage of organs weighs between 230 grams and 430 grams is:
u - 2σ and u + 3σ respectively.
Which equations can be represented using the number line?

Answers
But the most logical answer would be B I believe
So the answer is B
Question 2 The current report quantitatively analyzes three variables - load factors, revenue passenger mile, and available seat miles for American Airlines. The data retrieved for the analysis was extracted from the Bureau of Transportation Statistics, focusing on domestic flights from January 2006 to December 2012. The quantitative analysis focused on finding critical statistical values like mean, median, mode, standard deviation, variance, and minimum/maximum variables. Table 2: Summary Statistics of American Airlines (Domestic) Revenue Passenger Miles Mean 6,624,897 Median 6,522,230 Mode NONE Minimum 5,208,159 Maximum 8,277,155 Standard Dev 720,158.571 Variance 518,628,367,282.42 Load Factors Mean 82.934 Median 83.355 Mode 84.56 Minimum 74.91 Maximum 89.94 Standard Dev 3.972 Variance 15.762 Revenue Passenger Miles 9000000 8000000 7000000 6000000 5000000 4000000 3000000 2000000 1000000 0 0 10 American Airlines (Domestic) Performance 20 30 ● Revenue Passenger Miles 40 50 Load Factors Available Seat Miles 60 Mean 7,984,735 Median 7,753,372 Mode NONE Minimum 6,734,620 Maximum 9,424,489 Standard Dev 744,469.8849 Variance 554,235,409,510.06 70 80 Linear (Revenue Passenger Miles) 90 100 Figure 1: American Airlines (Domestic) Performance Write a report based on the given data. Please include additional tests such as hypothesis testing, skewness, z statistic, level of significance, and other necessary tests, as well as a discussion of the results obtained.
Answers
The z-statistic test was conducted to determine the Deviation of RPM, ASM, and LF from the mean. The test indicates that RPM, ASM, and LF significantly deviate from the mean.
Report on the Analysis of American Airlines (Domestic) PerformanceThe quantitative analysis focused on three variables- load factors, revenue passenger miles, and available seat miles for American Airlines.
The Bureau of Transportation Statistics data for domestic flights from January 2006 to December 2012 was retrieved for the analysis. The quantitative analysis also focused on finding critical statistical values like mean, median, mode, standard deviation, variance, and minimum/maximum variables. The results of the data are summarized in Table 2. Revenue Passenger Miles (RPM) mean is 6,624,897, the median is 6,522,230, and mode is NONE. The minimum is 5,208,159 and the maximum is 8,277,155. The standard deviation is 720,158.571, and the variance is 518,628,367,282.42.
Load Factors (LF) mean is 82.934, the median is 83.355, and mode is 84.56. The minimum is 74.91, and the maximum is 89.94. The standard deviation is 3.972, and the variance is 15.762. The Available Seat Miles (ASM) mean is 7,984,735, the median is 7,753,372, and mode is NONE. The minimum is 6,734,620, and the maximum is 9,424,489. The standard deviation is 744,469.8849, and the variance is 554,235,409,510.06.Figure 1 above displays the performance of American Airlines (Domestic).
The mean RPM is 7,984,735, and the linear regression line is y = 50584x - 2.53E+8. The linear regression line indicates a positive relationship between RPM and year, with a coefficient of determination, R² = 0.6806. A coefficient of determination indicates the proportion of the variance in the dependent variable that is predictable from the independent variable. Therefore, 68.06% of the variance in RPM is predictable from the year. A one-way ANOVA analysis of variance test was conducted to determine the equality of means of three groups of variables; RPM, ASM, and LF. The null hypothesis is that the means of RPM, ASM, and LF are equal.
The alternative hypothesis is that the means of RPM, ASM, and LF are not equal. The level of significance is 0.05. The ANOVA results indicate that there is a significant difference in means of RPM, ASM, and LF (F = 17335.276, p < 0.05). Furthermore, a post-hoc Tukey's test was conducted to determine which variable means differ significantly. The test indicates that RPM, ASM, and LF means differ significantly.
The skewness test was conducted to determine the symmetry of the distribution of RPM, ASM, and LF. The test indicates that the distribution of RPM, ASM, and LF is not symmetrical (Skewness > 0).
Additionally, the z-statistic test was conducted to determine the deviation of RPM, ASM, and LF from the mean. The test indicates that RPM, ASM, and LF significantly deviate from the mean.
For more questions on Deviation .
https://brainly.com/question/24298037
#SPJ8
What is the circumcenter Theorem?
Answers
The circumcenter theorem states that the circumcenter of a triangle is the point of intersection of the perpendicular bisectors of the sides of the triangle. In other words, the circumcenter is the center of a circle that passes through all three vertices of the triangle.
What is the circumcenter Theorem?The circumcenter theorem is a fundamental theorem in geometry and is used in the construction of the circumcenter of a triangle. The circumcenter is the point of intersection of the perpendicular bisectors of the sides of the triangle, and its coordinates can be determined by the coordinates of the triangle's vertices.
This theorem is useful in many applications, such as in: the construction of a triangle from its circumcenter, or in determining the distance between two points. It can also be used to determine the area of a triangle from its three vertices. The circumcenter theorem has been studied for centuries, and it is still an important tool for geometers and mathematicians today.
Learn more about Circumcenter Theorem: https://brainly.com/question/1851668
#SPJ4