Allison and her classmates planted bean seeds at the same time as Yuki and her classmates in Tokyo did. Allison is video-chatting with Yuki about their class seedlings. Who should expect to have the taller plant at the end of the school year?
PLZ HELP NOW
Allison's Plant: 2.5 inches in 5 days
Yuki's Plant: 5.5 centimeters in 4 days
(HINT: How can we change the rates to compare the growth rate of the seedlings)
Your answer:
Answers
Answer:
yukis plant
Step-by-step explanation:
Related Questions
a student needs to determine the density of an irregularly shaped object with a mass of . be sure each of your answer entries has the correct number of significant digits.
Answers
The density of an irregularly shaped object with a mass of 6.05 g is 5.50 g/mL.
We have to determine the density of an irregularly shaped object with a mass of 6.05 g.
The volume of the strangely formed object is the volume it displaces.
The volume displaced is the difference between the starting volume of water and the final volume of water when the object is submerged.
The value can be taken as 3.15 mL because the final volume of water in the diagram is between 3.10 and 3.20 mL.
Volume of object = volume displaced
Volume of object = final volume - initial volume
Volume of object = 3.15 mL - 2.05 mL
Volume of object = 1.10 mL
The following formula can then be used to calculate the object's density:
Density = mass / volume
Density = (6.05 g) / (1.10 mL)
Density = 5.50 g/mL
To learn more about density of an irregularly shaped link is here
brainly.com/question/28440634
#SPJ4
The complete question is:
A student needs to determine the density of an irregularly shaped object with a mass of 6.05 g.
Part A: The student fills a 10 mL graduated cylinder with deionized water. Use the image below to determine the volume of water in the graduated cylinder.
Report the answer to the correct number of significant figures. Initial volume of water = 2.05 mL

What ratio is the slope of a line that is perpendicular toy = (2/7)x + 5
Answers
Slope = -7/2
Explanations:The slope-Intercept form of the equation of a line is given as:
y = mx + c
where m represents the slope and
c represents the intercept
The given equation is:
\(y\text{ = }\frac{2}{7}x\text{ + 5}\)Comparing the equation above to y = mx + c
m = 2/7
The slope of the line perpendicular to y = mx + c is:
Slope = -1/m
Since m = 2/7
\(\begin{gathered} \text{Slope = -1 }\div\text{ }\frac{2}{7} \\ \text{Slope = -1}\times\frac{7}{2} \\ \text{Slope = }\frac{-7}{2} \\ \end{gathered}\)his composite figure is made of two identical pyramids attached at their bases. Each pyramid has a height of 2 units. 2 identical pyramids with rectangular bases are connected at their base. The height of the pyramid is 2. The lengths of the sides of the rectangle are 5 and 0.25 units. Which expression represents the volume, in cubic units, of the composite figure? One-half (One-third (5) (0.25) (2) ) One-half (One-third (5) (0.25) (4) ) 2(One-third (5) (0.25) (2) ) 2(One-third (5) (0.25) (4) )
Answers
The expression that will represent the volume of the identical rectangular base pyramid is: 2[One-third (5) (0.25) (2)] cubic units.
How to evaluate the expression for the volume of the identical pyramidTo calculate for the volume of a rectangular base pyramid, we use the formula:
volume = 1/3 × area of base rectangle × height
volume of one identical pyramid = (1/3 × 5 × 0.5 × 2)cubic units
volume of the two identical pyramid = 2(1/3 × 5 × 0.5 × 2)cubic units.
Therefore, the expression that will represent the volume of the identical rectangular base pyramid is: 2[One-third (5) (0.25) (2)] cubic units.
Read more about volume here:https://brainly.com/question/18994842
#SPJ1
George has a coin collection. 16% of the coins are quarters from the
1990s. If he has 32 quarters from the 1990s, how many total coins does he
have?
Answers
Answer:
200
Step-by-step explanation:
Given that :
16% of coins are quarters from 1990
Number of quarters from 1990 = 32
Since 16% = 32 quarters
The number of the total coins can be obtained thus :
Let the total number of coins = x
16% = 32
100% = x
Cross multiply :
0.16x = 32 * 1
0.16x = 32
x = 32 / 0.16
x = 200
Hence, total number of coins in the collection = 200
GIVING BRAINY AND EXTRA PTS NO LINKS GIVE EVIDENCE

Answers
Answer:
60
Step-by-step explanation:
I think that is the best choice sorry if i got it wrong.
Answer:
60 degrees
Step-by-step explanation:
Angle 1 is already 55 degrees, if you move the y line 5 degrees clockwise then it equals 60 degrees. Angle 1 and 3 are vertical angles so they are equal, if angle 1 is 60 degrees after we move the line then angle 3 is also 60 degrees
Thank you for taking the time out of your day to help me. Appreciate it.

Answers
Answer:
calculator gave me 6.5732
Step-by-step explanation:
Consider
the polynomials given below.
P = 1125 + 924 - 42³ 72² + 5
Q = (22² + 1) (42² - 3)
Determine the operation that results in the simplified expression below.
1125 + - 42³ - 52² + 8
O P Q
O
Ο
O
P+Q
PO
Q-P

Answers
The polynomial 11x⁵ + x⁴ - 4x³ - 5x² + 8 denotes the expression P - Q. The correct option is option A.
What is an expression?
A mathematical expression is a phrase that contains a minimum of two numbers or variables and at least one mathematical operation. It is possible to multiply, divide, add, or subtract in math. An expression has the following structure: Expression is (Math Operator, Number/Variable, Number/Variable)
Given polynomials are:
P = 11x⁵ + 9x⁴ - 4x³ - 7x² + 5
Q = (2x² + 1) (4x² - 3)
Simplify the polynomial Q = (2x² + 1) (4x² - 3):
Q = (2x² + 1) (4x² - 3)
Q = 2x²(4x² - 3) + 1(4x² - 3)
Q = 8x⁴ - 6x² + 4x² - 3
Add like terms:
Q = 8x⁴ - 2x² - 3
Now calculate P + Q
P + Q = 11x⁵ + 9x⁴ - 4x³ - 7x² + 5 + 8x⁴ - 2x² - 3
Combine like terms:
P + Q = 11x⁵ + (9x⁴ + 8x⁴) - 4x³ + (- 7x² - 2x²) + 5 - 3
P + Q = 11x⁵ + 17x⁴ - 4x³ - 9x² + 2
Now calculate P - Q
P - Q = 11x⁵ + 9x⁴ - 4x³ - 7x² + 5 - (8x⁴ - 2x² - 3)
P - Q = 11x⁵ + 9x⁴ - 4x³ - 7x² + 5 - 8x⁴ + 2x² + 3
P - Q = 11x⁵ + (9x⁴ - 8x⁴) - 4x³ + (-7x² + 2x² )+ (5 + 3)
P - Q = 11x⁵ + x⁴ - 4x³ - 5x² + 8
Now calculate Q - P
Q - P = 8x⁴ - 2x² - 3 - (11x⁵ + 9x⁴ - 4x³ - 7x² + 5)
Q - P = 8x⁴ - 2x² - 3 - 11x⁵ - 9x⁴ + 4x³ + 7x² - 5
Combine like terms:
Q - P = - 11x⁵ + (8x⁴ - 9x⁴) + 4x³ + (- 2x² + 7x²) - 3 - 5
Q - P = - 11x⁵- x⁴ + 4x³ + 5x² - 8
To learn more about operation, click on the below link:
https://brainly.com/question/22735845
#SPJ1
A sports car manufacturer paints its cars silver, white, black, and red in the following proportions: ?
Color: Silver White Black Red
Proportion: .2 .3 .1 .4
We know that 40% of these cars are manufactured with tan leather upholstery while the remaining 60% are manufactured with gray leather.
A. Assuming that the choice of exterior color and leather color are independent, what is the probability that a randomly selected sports car from this manufacturer will be white with gray upholstery?
B. Assuming that we know the car has tan upholstery, what is the probability that the car is either silver or white?
Answers
Answer:
A. The probability that a randomly selected sports car from this manufacturer will be white with gray upholstery is P=0.12.
B. Assuming that we know the car has tan upholstery, the probability that the car is either silver or white is P=0.50.
Step-by-step explanation:
We first start by stating that the events "exterior color" and "leather color" are independent, so the probability of the outcomes of each event is not affected by the outcomes of the other event.
A. The probability of having a car that is white (W) with gray upholstery (G) is equal to the probability of having a car that is white multiplied by the probability of having a car with gray leather upholstery. Mathematically, this is:
\(P(\text{W\&G})=P(W)\cdot P(G)=0.3\cdot 0.4=0.12\)
B. As the events are independent, the probability of having a silver or white car, given that the car has tan upholstery, is the same as the probabiltiy of having a silver or white car:
\(P(S\,or\,W | T)=P(S\,or\,W)=P(S)+P(W)=0.20+0.30=0.50\)
Reggie is planning to visit a clients office. He is taking a plane to get there, and the flight is scheduled to take five hours. But the flight will be delayed by more than an hour because of bad weather. Reggie wants to call the airport hotel until the hotel manager when he will be arriving at the hotel. The variable X gives the elapsed time between ready schedule departure and his arrival at the hotel. Write an inequality for X, the time that passes between Reggie schedule departure in his arrival at the hotel.
Answers
Answer: x>6
Step-by-step explanation:
A package of 25 fishing hooks costs $9.95 , while a package with 40 hooks costs $13.99 . Which is the better buy? Round your answer to the nearest cent if necessary.
Answers
Therefore, the package with 40 hooks is the better buy in terms of cost efficiency.
To determine which package is the better buy, we need to compare the cost per hook for each package.
For the package of 25 hooks costing $9.95, we divide the total cost by the number of hooks:
Cost per hook = $9.95 / 25 = $0.398
Rounding to the nearest cent, the cost per hook is $0.40.
For the package of 40 hooks costing $13.99, we divide the total cost by the number of hooks:
Cost per hook = $13.99 / 40 = $0.3498
Rounding to the nearest cent, the cost per hook is $0.35.
Comparing the two costs per hook, we can see that the package with 40 hooks for $13.99 offers a better deal, as the cost per hook is lower at $0.35.
For such more question on package
https://brainly.com/question/12251427
#SPJ8
The perimeter of the triangle shown is 225 feet, find the length of each side
X feet = How many Feet?
5x feet = how many feet?
(6x - 3) feet = for many feet?

Answers
Answer:
I have solved it and attached in the explanation.
Step-by-step explanation:


which expression below is equal to -18 -8(2)+5_8+2(-5)_8+2(5)-8(5)+2
Answers
- 8 + 2(- 5)
- 8 - 10
= - 18
The correct answer is the second option
Find each missing measure
PLS HURRY WILL GIVE BRANLIEST. DON'T RESPOND WITH LINKS
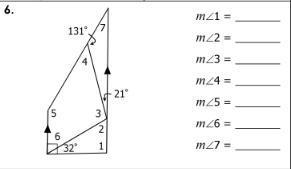
Answers
Answer: 1 = 90 2=58 3=90 6=58 7=8
Step-by-step explanation:
I don’t know what 4 and 5 are
solve the PDE using separation of variables method Uxx = 1/2 Ut 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Answers
The general solution of the partial differential equation is:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
How to solve Partial Differential Equations?The partial differential equation (PDE) is given as:
Uxx = (1/2)Ut with the boundary and initial conditions as 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Assume that the solution can be written as a product of two functions:
U(x, t) = X(x)T(t)
Substituting this into the PDE, we have:
X''(x)T(t) = (1/2)X(x)T'(t)
Dividing both sides by X(x)T(t), we get:
(X''(x))/X(x) = (1/2)(T'(t))/T(t)
Since the left side only depends on x and the right side only depends on t, both sides must be equal to a constant, denoted as -λ²:
(X''(x))/X(x) = -λ²
(1/2)(T'(t))/T(t) = -λ²
Simplifying the second equation, we have:
T'(t)/T(t) = -2λ²
Solving the second equation, we find:
T(t) = Ce^(-2λ²t)
Applying the boundary condition U(0, t) = 0, we have:
U(0, t) = X(0)T(t) = 0
Since T(t) ≠ 0, we must have X(0) = 0.
Applying the boundary condition U(3, t) = 0, we have:
U(3, t) = X(3)T(t) = 0
Again, since T(t) ≠ 0, we must have X(3) = 0.
Therefore, we can conclude that X(x) must satisfy the following boundary value problem:
X''(x)/X(x) = -λ²
X(0) = 0
X(3) = 0
The general solution to this ordinary differential equation is given by:
X(x) = Asin(λx) + Bcos(λx)
Applying the initial condition U(x, 0) = 5*sin(4πx), we have:
U(x, 0) = X(x)T(0) = X(x)C
Comparing this with the given initial condition, we can conclude that T(0) = C = 5.
Therefore, the complete solution for U(x, t) is given by:
U(x, t) = Σ [Aₙsin(λₙx) + Bₙcos(λₙx)]*e^(-2(λₙ)²t)
where:
Σ represents the summation over all values of n
λₙ are the eigenvalues obtained from solving the boundary value problem for X(x).
To find the eigenvalues λₙ, we substitute the boundary conditions into the general solution for X(x):
X(0) = 0: Aₙsin(0) + Bₙcos(0) = 0
X(3) = 0: Aₙsin(3λₙ) + Bₙcos(3λₙ) = 0
From the first equation, we have Bₙ = 0.
From the second equation, we have Aₙ*sin(3λₙ) = 0. Since Aₙ ≠ 0, we must have sin(3λₙ) = 0.
This implies that 3λₙ = nπ, where n is an integer.
Therefore, λₙ = (nπ)/3.
Substituting the eigenvalues into the general solution, we have:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
where Aₙ are the coefficients that can be determined from the initial condition.
Read more about Partial Differential Equations at: https://brainly.com/question/28099315
#SPJ1
HELP ME AND ANSWER THIS IK ITS -1 BUT ITS AN MULTIPLE CHOICE!! please don't guess thank you :) and I'll mark you as Brainlest :D

Answers
Answer:
C and D
Step-by-step explanation:
Let's solve for x to see what range the answer has to be in:
-2x - 3 ≤ -1
-2x ≤ 2
x ≥ -1
So the value of x must be larger than or equal to -1. So the answers would be 1 and 0
It is assumed that the test results for a class follow a normal distribution with a mean of 78 and a standard deviation of 36. If you know that a student's grade is greater than 72, what is the probability that it is greater than 84
Answers
Answer: 0.4337
Step-by-step explanation:
Let X represents the test results for a class that follow a normal distribution .
Given: Mean \(\mu=78\), Standard deviation \(\sigma=36\)
Then, the probability that it is greater than 84 will be
\(P(X>84)=P(\dfrac{X-\mu}{\sigma}>\dfrac{84-78}{36})\\\\=P(Z>0.167)\ \ \ [Z=\dfrac{X-\mu}{\sigma}]\\\\=1-P(Z<0.167)\\\\=1-0.5663=0.4337\ [\text{By p-value table}]\)
Hence, the required probability = 0.4337
Use the limit definition of the derivative to find the slope of the tangent line to the curve f(x) = 7x ^ 2 + 2x + 3 at x = 1
Answers
Answer:
16
Step-by-step explanation:
Step 1: Write down the function \(f(x)=7x^2+2x+3.\)
Step 2: Write down the limit definition of the derivative:
\(f'(x)= lim_{h0} \frac{f(x+h)=f(x)}{h} .\)
Step 3: Substitute the function \(f(x)\) into the limit definition:
\(f'(x)=lim_{h0} \frac{(7(x+h)^2+2(x+h)+3)-(7x^2+2x+3)}{h}.\)
Step 4: Simplify the expression inside the limit:
\(f'(x)=lim_{h0}\frac{7x^2+14xh+7h^2+2x+2h+3-7x^2-2x-3}{h} .\)
Step 5: Combine like terms:
\(f'(x)=lim_{h0} \frac{14xh+7h^2+2h}{h} .\)
Step 6: Factor out an \(h\) from the numerator:
\(f'(x)=lim_{h0} \frac{h(14x+7h+2h}{h} .\)
Step 7: Cancel out the \(h\) in the numerator and denominator:
\(f'(x)=lim_{h0}(14x+7h+2).\)
Step 8: Evaluate the limit as \(h\) approaches 0:
\(f'(x)=14x+2.\)
Step 9: Substitute \(x=1\) into the derivative:
\(f'(1)=14(1)+2=14+2=16.\)
The Slope of the tangent line to the curve \(f(x)=7x^2+2x+3\) at \(x=1\) would be \(16.\)
Help me please I beg

Answers
Answer:
Exact Form:
1/22
Decimal Form:
0.045
Step-by-step explanation:
What are roots of the equation -90=x (x-18)
Answers
Answer:
-90=\(x\)(\(x\)-18)
-90=\(x^{2}\)-18\(x\)
\(0=x^{2}-18x+90\)
\(x=9+3i or 9-3i\)
Step-by-step explanation:
you need to use quadratic formula and you will find square root a negative ( -9 ), which is an imaginary no.
square root (-9) = 3i
Multiply 2 times 27 using the area model label the model
Answers
Answer:
54
Step-by-step explanation:
2×27=54 hope this helps
Help me please!!!
Whoever answers right gets brainliest!

Answers
The equation that best describes the relation is y = -x+1 ( optionD)
What is linear equation?A linear equation is an algebraic equation of the form y=mx+b. involving only a constant and a first-order (linear) term, where m is the slope and b is the y-intercept.
Taking x(0,1) and y ( 1,0)
therefore the slope of the line
= 0-1/1-0
= -1/1 = -1
the equation a line is given as
y-y1 = m(x-x1)
= y-1 = -1( x - 0)
= y-1 = -x
y = -x +1
therefore the equation that describe relation is y = 1-x or y = -x+1
learn more about linear equation from
https://brainly.com/question/2030026
#SPJ1
amplitude and period of y = 1 + cos 0
Answers
Amplitude and period of y = 1 + cos 0 are amplitude: = 1 and period: 2π respectively.
The cosine function cosx is one of the basic functions encountered in trigonometry
y = 1 + cos 0
Rewrite the expression as
−cos(x)+1.
Use the form
acos(bx−c)+d
To find the variables used to find the amplitude, period, phase shift, and vertical shift.
a =-1
b =1 = d
c=0
Find the amplitude
Let
Amplitude: = 1
Phase Shift: = 0
List the properties of the trigonometric function.
Amplitude: 1
Period: 2π
Phase Shift: None
Vertical Shift: 1
So the amplitude and period of the equation y = 1 + cos 0 are 1 and 2 correspondingly.
To learn more about trigonometric function.: brainly.com/question/13256520
#SPJ1
The amplitude and period of the equation y = 1 + cos 0 are 1 and 2 correspondingly.
The cosine formula One of the fundamental trigonometry functions is cosx.
y = 1 + cos 0
Change the wording to
−cos(x)+1.
Apply the form
acos(bx−c)+d
to identify the parameters used to calculate the vertical shift, phase shift, amplitude, and period.
a =-1
b =1 = d
c=0
Measure the amplitude.
Let
Amplification: 1
0 for phase shift
Describe the trigonometric function's characteristics.
1 amplitude
Duration: 2
No phase shift
Shift Vertically: 1
As a result, y = 1 + cos 0 has an amplitude and period of 1 and 2, respectively.
Javier bought a painting for
$
150
$150dollar sign, 150. Each year, the painting's value increases by a factor of
1.15
1.151, point, 15.
Which expression gives the painting's value after
7
77 years?
Choose 1 answer:
Choose 1 answer:
(Choice A)
(
150
⋅
1.15
)
7
(150⋅1.15)
7
left parenthesis, 150, dot, 1, point, 15, right parenthesis, start superscript, 7, end superscript
A
(
150
⋅
1.15
)
7
(150⋅1.15)
7
left parenthesis, 150, dot, 1, point, 15, right parenthesis, start superscript, 7, end superscript
(Choice B)
150
⋅
1.1
5
7
150⋅1.15
7
150, dot, 1, point, 15, start superscript, 7, end superscript
B
150
⋅
1.1
5
7
150⋅1.15
7
150, dot, 1, point, 15, start superscript, 7, end superscript
(Choice C)
(
150
+
1.15
)
⋅
7
(150+1.15)⋅7left parenthesis, 150, plus, 1, point, 15, right parenthesis, dot, 7
C
(
150
+
1.15
)
⋅
7
(150+1.15)⋅7left parenthesis, 150, plus, 1, point, 15, right parenthesis, dot, 7
(Choice D)
150
+
1.15
⋅
7
150+1.15⋅7150, plus, 1, point, 15, dot, 7
D
150
+
1.15
⋅
7
150+1.15⋅7
Answers
The correct expression is \($(150 \cdot 1.15)^7$\) (Choice A).
The problem states that the painting's value increases by a factor of 1.15 each year. This means that the value at the end of each year is 1.15 times the value at the beginning of the year. Therefore, after one year, the value of the painting is\($150 \cdot 1.15 = 172.50$\).
To find the value after 7 years, we need to multiply the value of the painting each year by 1.15 a total of 7 times. This can be represented mathematically as \($(150 \cdot 1.15)^7$\). This expression is equal to the starting value of the painting, 150, multiplied by 1.15$ raised to the 7th power, which represents the 7 years of appreciation.
If we were to choose expression B, it would give an incorrect result because it uses a value of 1.1 instead of 1.15 to represent the yearly increase in value.
Expressions C and D are also incorrect because they are not taking into account the compounding effect of the yearly increase. Expression C adds the initial value and the total years together, and expression D adds the initial value to the yearly increase multiplied by 7, neither of which correctly reflects the exponential growth of the painting's value.
For such more questions on expression
https://brainly.com/question/1859113
#SPJ8
The graph shows the distribution of the lengths (in seconds) of videos on a popular video-streaming site. The distribution is approximately Normal, with a mean of 264 seconds and a standard deviation of 75 seconds.
A graph titled Streaming Videos has length (seconds) on the x-axis, going from negative 36 to 564. The highest point of the curve is at 264.
What percentage of videos on the streaming site are between 264 and 489 seconds?
0.15%
49.85%
95%
99.7%
Answers
According to the properties of the standard normal distribution, approximately 99.7% of the values lie within three standard deviations of the mean. Therefore, the answer is 99.7%.
To determine the percentage of videos on the streaming site that are between 264 and 489 seconds, we need to calculate the area under the normal curve within that range. Since the distribution is approximately normal with a mean of 264 seconds and a standard deviation of 75 seconds, we can use the properties of the standard normal distribution to find the desired percentage.
First, we need to convert the values 264 and 489 to z-scores, which represent the number of standard deviations a particular value is away from the mean. The z-score formula is given by:
z = (x - μ) / σ
where x is the value, μ is the mean, and σ is the standard deviation. Plugging in the values, we get:
z1 = (264 - 264) / 75 = 0
z2 = (489 - 264) / 75 = 3
Next, we can use a standard normal distribution table or a calculator to find the area under the curve between z = 0 and z = 3. The area represents the percentage of videos falling within that range. The answer is 99.7% .
For more such questions on normal distribution
https://brainly.com/question/4079902
#SPJ8
A garden table and a bench cost 735 combined. The garden table costs 35 more than the bench. What is the cost of the bench?
Answers
Answer:
350
Step-by-step explanation:
Let,
x = bench
x + 35 = garden table
EQUATION:
(x) + (x + 35) = 735
2x = 735 - 35
2x = 700
x = 350
SUBSTITUTE:
bench costs 350 and garden table costs 385
Hello!
Based on the info we have we can form 2 equations :
(Keep in mind x is the cost of the garden table and y is that of the bench)
x + y = 735x = y + 35Now substitute x in the first equation.
⇒ y + 35 + y = 735
⇒ 2y = 700
⇒ y = 350
∴ The cost of the bench is \(\fbox {350}\)
PLSSSS HELPPP I WILL FIVE BRAINLY!!!!

Answers
Answer:
The first box : -4 the second one : 6
Step-by-step explanation:
subtract 7 from 3 for the first box, then add 10 to -4 for the second one.
simple ratio of 13km to 3km
Answers
The simple ratio of 13 km to 3 km as required to be determined in the task content is; 13 : 3.
What is the simple ratio of 13km to 3km?It follows from the task content that the simple ratio of 13 km to 3 km is to be determined as required.
On this note, we have that;
13 km to 3 km.
which results to;
13 : 3
However, since 13 and 3 have no common factors except 1; it follows that the result as a simple ratio is; 13 : 3.
Read more on simple ratio;
https://brainly.com/question/29272642
#SPJ1
Nicole will attend a 2-year college, and she is planning her budget.
Answer the following.
(a) Below is an estimate of all her expenses and sources of funding for her 2-year college
education.
For each, select whether it is an expense or a source of funding.
Expense
Funding
Books and supplies:
Savings:
Scholarships:
Housing and food:
Tuition and fees:
Transportation:
$1700
$7800
$10,240
$14,020
$11,660
$2040
$11,600
$6200
$2980
Grants:
Student loans:
Personal expenses:
(b) What is the total of her estimated expenses?
$
0000
0000 1000
X
Answers
a. Expenses: Books and supplies, Housing and food, Tuition and fees, Transportation and Personal expenses. Funding: Savings,
Scholarships, Grants and Student loans.
b. Total estimated expenses are $29,400
(a) Below is an estimate of all her expenses and sources of funding for her 2-year college education.
Expense:
Books and supplies: $1700
Housing and food: $14,020
Tuition and fees: $11,660
Transportation: $2040
Personal expenses: $2980
Funding:
Savings: $7800
Scholarships: $10,240
Grants: $11,600
Student loans: $6200
(b) What is the total of her estimated expenses?
To find the total estimated expenses, we need to add up all the expenses mentioned:
$1700 + $14,020 + $11,660 + $2040 + $2980 = $29,400
Therefore, the total estimated expenses for Nicole's 2-year college education is $29,400.
For more such questions on Expenses, click on:
https://brainly.com/question/30967676
#SPJ8
Write the following expression as a constant, a single trigonometric function, or a power of a trigonometric function.
sec x cos x
Answers
Answer:
1.
Step-by-step explanation:
sec x cos x
= 1/cos x * cos x
= cos x / cos x
= 1.
A dilation is a transformation in which the _____, but not the shape, of a geometric figure is changed.
Answers
no explanation really
like dilation 2x, 2y makes the size bigger but the shapes rhe same