after simplifying expressions on each side of an equation you observed that the coefficients of x and the constants on each side of the equal sign were sign
Answers
Upon simplifying the expressions on each side of an equation, I noticed that the coefficients of x and the constants on each side of the equal sign were zero.
When simplifying expressions in an equation, we aim to rearrange and combine like terms to simplify the equation. In this particular scenario, after performing the simplification, it became apparent that the coefficients of x, which represent the numerical factors multiplying x, were equal to zero on both sides of the equation. Similarly, the constants, which are the terms without variables, were also zero on both sides.
An equation where the coefficients of x and the constants are zero on each side is known as a trivial equation. In this case, the equation doesn't contain any variables or unknowns, as both sides reduce to zero. Consequently, the equation holds true for all values of x since any value substituted for x will result in zero on both sides of the equation, making it an identity.
Trivial equations are distinct from other types of equations because they don't involve any variable-dependent relationships or solutions. While they may not have any practical significance in most situations, they can arise in mathematical manipulations or as special cases in certain mathematical contexts. It is crucial to recognize and differentiate trivial equations from other types of equations to ensure accurate problem-solving and analysis.
To summarize, upon simplifying the expressions on each side of an equation, I observed that the coefficients of x and the constants were zero on both sides. This leads to a trivial equation, where the equation holds true for all values of x. Trivial equations lack variable-dependent relationships and have no practical significance in most cases, but they are important to recognize in mathematical contexts.
Learn more about coefficients here
https://brainly.com/question/30845099
#SPJ11
Related Questions
Emma has completed 70% of her summer reading list. She has read 14 books so far. How many books are there on her summer reading list? Explain
Answers
The number of books in her summer reading list is = 20
The number of books that has been read by Emma = 14
The percentage of books that has been read by Emma = 70%
But the percentage of books in Emma summer reading list = 100%
∴ The number of books in her reading list= ˣ
That is ;
70% = 14
100% = ˣ
Make ˣ the subject of formula,
ˣ = 100 × 14 / 70
ˣ = 20
Learn more here:
https://brainly.com/question/20766171
A polygon will be dilated on a coordinate grid to create a smaller polygon. The polygon is dilated usi X
the origin as the center of dilation.
Which rule could represent this dilation?
A. (x,y) → (0.5 – x,0.5 - y)
B. (x,y) → (x - 7, y - 7)
C. (x,y) - (x, y)
D. (x,y) → (0.9x, 0.9y)
Answers
Answer:
D). (x, y) --> (0.9x, 0.9y).
Step-by-step explanation:
You multiply each coordinate to create a dilation . To get a smaller image the cinstant of multiplication is less than 1.
So it is D
need help with homework it was due the 15th
Answers
That's where the lines overlap
The 8 is counted on the x axis which is the horizontal one of the one laying down because it's 8 across to where the lines overlap
The 4 is counted on the y axis which is vertical or the one standing up. It's 4 because to get to where the lines overlap you'd have to go up 4
Here the correct answer is (8,4) means option B.
Given equations are,
y=x-4 -----------------(1)
y= -0.5x+8-----------(2)
Option A.(4,2): If we put x=4 in equation one then y=0 which does not satisfy equation 2.
Option B.(8,4): If we put x=8 in equation one then y=4 and which satisfies equation 2.
Option C.(2,4): If we put x=2 in equation one then y=-2 which does not satisfy equation 2.
Option D.(4,8): If we put x=4 in equation one then y=0 which does not satisfy equation 2.
Therefore the solution of the equations y=x-4 and y=-0.5x+8 is (8,4) which is option B.
Learn more about quadratic equations:
https://brainly.com/question/24737967
the ratio of the short side of a certain rectangle to the long side is equal to the ratio of the long side to the diagonal. what is the square of the ratio of the short side to the long side of this rectangle?
Answers
As per the Pythagoras theorem, the ratio of the short side to the long side of this rectangle is (√5 - 1)/ 2
In math Pythagoras theorem is defined as the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse
Here we have given that the ratio of the short side of a certain rectangle to the long side is equal to the ratio of the long side to the diagonal.
And we need to find is the square of the ratio of the short side to the long side of this rectangle
While we looking into the given question we have identified that the short side of the rectangle be a and let the long side of the rectangle be b.
Therefore, the diagonal, according to the Pythagorean Theorem, is
√(a²+b²)
Now we can write the equation:
a / b = b /√ a² + b²
Then we have to find the square of the ratio of a to b.
Let us consider the answer, be k.
When we squaring the above equation,
a²/ b² = b² / a² + b² = k
When we solve this one then we get the value of k = 1.
Now we have to Multiply each side of the equation by k,
=> k² = 1 - k.
And then adding each side by k,
k² + k − 1 = 0.
Now, we have to Solving for k using the Quadratic Formula,
= > k = -1 ± √[1² − 4(1)(−1)] / 2
=> k = -1±√5/2
As we know that the ratio of lengths and diagonals of a rectangle cannot be negative.
Therefore, the resulting value is √5 - 1/2
To know more about Pythagoras theorem here
https://brainly.com/question/343682
#SPJ4
Matt has a bag with 3 red counters and 7 green counters. Matt picks a counter at random, and then picks another counter. Using the tree diagram drawn above, work out the probability that Matt does not get any red counters.
Answers
Answer: 0.47
Step-by-step explanation:
The probability that Matt does not get any red counters is equal to the probability that in both random selections, Matt gets a green counter.
For the first selection, we have a total of 10 counters, 3 red and 7 green, then the probability of getting a green one is:
p = 7/10.
For the second selection, we have 9 counters, 3 red and 6 green (because one green is already taken)
then the probability of getting a green one is:
p = 6/9
And the joint probability of both events is equal to the product of the probability of each event, this is:
p = (7/10)*(6/9) = 42/90 = 0.47
Multiply 3 by the number of apples in each bag x and add it to 3 times the number of bananas in each bunch y an then multiply that sum by 3
Answers
Answer:
9(x+y)
(3x + 3y) 3
Need help!!!!!! ASAP
Answers
Answer:
og
Step-by-step explanation:
Lisa is on the west shore of Mighty River, which is 1 mile wide and has two parallel shorelines running exactly north-to-south. She wishes to get to a point on the opposite shore that is 1 mile south of where she is now as quickly as possible. (So this point is sqrt (2) miles due southeast from her starting position.) Assuming that Lisa can walk twice as fast as she can swim, and that she wants to swim across the river first before walking any necessary distance along the opposite shoreline, at what course (in degrees) should she start swimming?
(The angle is measured from north, so 90 degrees is due east, meaning she swims directly across the river, and 135 degrees is due southeast, meaning she swims directly to her destination point.)
Answers
Lisa should start swimming at an angle of \(120^{\circ}\) to reach her destination as quickly as possible.
Given:
The river is 1 mile wideThe end point is 1 mile south of the starting pointLisa's speed of walking is twice that of her speed of swimmingLisa wants to swim across the river first before walking the rest of the distance along the opposite shorelineTo find: The course (in degrees) at which she should start swimming so that she can reach the end point as quickly as possible
To solve this problem, we need to know the following:
Pythagoras theorem states that in a right angled triangle, the square of the length of hypotenuse is the sum of the squares of lengths of perpendicular and baseCosine of an angle is the ratio of base and hypotenuse in the right angled triangleA single variable function is minimized by a value for which, the first derivative of the function is zero and the second derivative of the function is positiveLet us assume that Lisa starts swimming at a course such that she needs to swim for 'x' miles to reach the opposite shore, as shown in the figure.
Labelling the points in the figure, we can say that,
AB = 1 mile (given)
BD = 1 mile (given)
AC = x miles (by our assumption)
It is clear that ABC forms a right angled triangle where,
Perpendicular: BC
Base: AB
Hypotenuse: AC
Using Pythagoras Theorem for triangle ABC, we have,
\((Hypotenuse)^{2} =(Perpendicular)^{2} +(Base)^{2}\), which implies,
\((AC)^{2} =(BC)^{2} +(AB)^{2}\)
Put AC = x, AB = 1 in the above equation to get,
\(x^{2} =(BC)^{2} +1^{2}\)
\(x^{2} =(BC)^{2} +1\)
\((BC)^{2}=x^{2} -1\)
\(BC=\sqrt{x^{2} -1}\)
From the figure, we can say that,
\(CD=BD-BC\)
Put \(BC=\sqrt{x^{2} -1}\) and \(BD=1\) in the above equation to get,
\(CD=1-\sqrt{x^{2} -1}\)
According to our assumption, Lisa swims the distance of AC and walks the distance of CD, that is, she swims a distance of \(x\) miles and walks a distance of \(1-\sqrt{x^{2} -1}\) miles.
Now, let us assume that Lisa's speed of swimming is \(k\) miles/hour. It is given that Lisa's speed of walking is twice that of her speed of swimming. Then, accordingly, Lisa's speed of walking must be \(2k\) miles/hour. We note that these speeds are constants for Lisa.
We know that,
\(Speed=\frac{Distance}{Time}\)
Then,
\(Time=\frac{Distance}{Speed}\)
This implies that,
Time spent by Lisa on swimming = \(\frac{x}{k}\)
Similarly, time spent by Lisa on walking = \(\frac{1-\sqrt{x^{2} -1} }{2k}\)
Then, total time taken by Lisa to travel the whole distance from the starting point to the end point is,
\(\frac{1-\sqrt{x^{2} -1} }{2k} +\frac{x}{k}\)
\(\frac{1}{2k}( 1-\sqrt{x^{2} -1} +2x )\)
Since Lisa wishes to get to the end point as quickly as possible, we must minimize the total time taken by her to travel the entire distance.
Total time taken: \(T=\frac{1}{2k}( 1-\sqrt{x^{2} -1} +2x )\)
Differentiating with respect to 'x', we have,
\(T'=\frac{1}{2k}( -\frac{x}{\sqrt{x^{2} -1}} +2 )\)
Differentiating with respect to 'x' again, we have,
\(T''=\frac{1}{2k(\sqrt{x^{2} -1})^{3}}\)
Equating the first derivative to 0, we have,
\(\frac{1}{2k}( -\frac{x}{\sqrt{x^{2} -1}} +2 )=0\)
\(-\frac{x}{\sqrt{x^{2} -1}} +2 =0\)
\(\frac{x}{\sqrt{x^{2} -1}} =2\)
\(2\sqrt{x^{2} -1}= x\)
Squaring both sides,
\(4(x^{2} -1)= x^{2}\)
\(4x^{2} -4= x^{2}\)
\(3x^{2} =4\)
\(x^{2} =\frac{4}{3}\)
\(x=\frac{2}{\sqrt{3}}\)
Note that we assumed the positive square root for 'x' because 'x' denotes a distance which cannot be negative.
Put \(x=\frac{2}{\sqrt{3}}\) in the expression for second derivative to get,
\(T''=\frac{1}{2k(\sqrt{(\frac{2}{\sqrt{3}} )^{2} -1})^{3}}\)
\(T''=\frac{1}{2k(\sqrt{\frac{4}{3} -1})^{3}}\)
\(T''=\frac{1}{2k(\sqrt{\frac{1}{3}})^{3}}>0\)
The last expression is positive because 'k' denotes a speed which is always positive.
This implies that the obtained value \(x=\frac{2}{\sqrt{3}}\) minimizes the quantity of total time taken.
Now, from the figure, we can say that,
\(cos(\angle BAC)=\frac{AB}{AC}\)
Put AC = x, AB = 1 in the above equation to get,
\(cos(\angle BAC)=\frac{1}{x}\)
Put the obtained minimizing value, \(x=\frac{2}{\sqrt{3}}\) in the above equation to get,
\(cos(\angle BAC)=\frac{1}{\frac{2}{\sqrt{3}} }\)
\(cos(\angle BAC)=\frac{\sqrt{3}}{2 }\)
\(cos(\angle BAC)=cos(30^{\circ})\)
Then,
\(\angle BAC=30^{\circ}\)
Since the angle is measured from the north, the required angle is, \(90^{\circ}+30^{\circ}=120^{\circ}\)
Thus, Lisa should start swimming at an angle of \(120^{\circ}\) to reach her destination as quickly as possible.
Learn more about finding optimum course here:
https://brainly.com/question/17587668
Kim has $400 in her savings account. If she spends $50, how much will her account decrease?
Answers
Answer:
$350 left lost 50$
Step-by-step explanation:
The concession stand at the high school football stadium sells hot dogs and sodas. Jack bought 3 hotdogs and 2 sodas for a total of $12. Angie bought 1 hotdog and 4 sodas for $9. Solve a system of equations to determine the cost of 1 hotdog and 1 soda.
Answers
Answer: each soda costs $1.5 and each hotdog costs $3.
Step-by-step explanation:
If H is the price for one hotdog and S is the price for one soda, we have the equations:
for Jack.
3*H + 2*S = $12
For Angie.
1*H + 4*S = $9
Now we can isolate one of the variables in one of the equations and then replace it in the other equation, let's isolate H in the second equation:
H = $9 - 4*S
now we replace it in the first eq
3*H + 2*S = $12
3*($9 - 4*S) + 2*S = $12
$27 - 12*S + 2*S = $12
-10*S = $12 - $27 = -$15
S = $15/10 = $1.5
Now we can replace it in the equation for H and get:
H = $9 - 4*$1.5 = $3
So each soda costs $1.5 and each hotdog costs $3.
Answer: One hotdog cost $3 and One soda costs $1.5
Step-by-step explanation:
Let hotdogs be denoted by h
Let sodas be denoted as s
Jack bought 3 hotdogs and 2 sodas for a total of $12. This can be written as:
3h + 2s = 12
Angie bought 1 hotdog and 4 sodas for $9. This can be written as:
h + 4s = 9
3h + 2s = 12
h + 4s = 9
1 × (3h + 2s = 12)
3 × (h + 4s = 9)
3h + 2s = 12
3h + 12s = 27
Subtract the equation
-10s = -15
s = -15/-10
s = 1.5
One soda cost $1.5
Since h + 4s = 9
h + 4(1.5) = 9
h = 9 - 6
h = 3
One hotdog costs $3
What is 8,743 divided by 4
Answers
Answer:
2185 \(\frac{3}{4}\)
Step-by-step explanation:
Question:
What is 8,743 divided by 4?
Explanation:
Heya, I heard you need help! Well, let me explain for ya! c:
Step 1: Divide.
- First, you would write down the division problem using long division, let me show you how:
1. Write it down in long division form.
2. 4 can go into 8 2 times, so subtract that by 8 to get a difference of 0.
3. Subtract 8 by 8 and get a difference of 0.
4. 4 cannot go into 0, so bring down the 7.
5. 4 goes into 7 1 time, so you would subtract 7 by 4 to get a difference of 3.
6. 4 cannot go into 3, so bring down the 4.
7. 4 goes into 34 8 times, so you would subtract 34 by 32 to get a difference of 2.
8. 4 does not go into 2, so bring down the 3.
9. 4 goes into 23 5 times, so you subtract 23 by 20 to get a difference of 3.
10. 4 does not go into 3, so you bring down an imaginary 0 and add a decimal on the left of the 3 in 8743.
11. 4 goes into 30 7 times as 7 times 4 is 28, so subtract 30 by 28 to get a difference of 2.
12. Finally, you bring down another 0 as 4 cannot go into 2. Then, you subtract 20 by 20 to get 0.
- Your quotient is 2185.75.
Step 2: Converting to a mixed number.
- This is the easiest part. All you have to do is convert 75/100 into simplest form as 75/100 is the decimal in fraction form. This will get you 3/4.
- Then, you would write 2185 \(\frac{3}{4}\).
Therefore, your answer is 2185 \(\frac{3}{4}\)
Also, sorry about that book for a math problem.
Hope that helped! If you have anymore questions, just comment down and I will try my best to help you! Au revoir!
~ Sienna
AT HOME / STUDENTS
1. What are the two equations you created?
id to find 2. How did you put the equations into y=mx+b form?
3. Using your calculator, explain the steps that you did to find
the intersection point.
4. What is the answer?
Answers
pls help if you know it
during a high school basketball game the home team scored 51 points and the opponent's score 62 points what is the point differential for (the difference between the number of points scored by a team and its opponent) for the home team?
-11
11
-10
10
Answers
Answer:
11
Step-by-step explanation:
just do 62-51=11 which gets you the difference between points
Solve for x. I NEED HELP ASAP!
Answers
Answer:
x = 105
Step-by-step explanation:
The sum of the interior angles of a polygon is
sum = 180° (n - 2) ← n is the number of sides
Here n = 7, thus
sum = 180° × 5 = 900°
Sum the interior angles and equate to 900
x + 102 + 165 + 123 + x + 11 + 128 + 161 = 900, that is
2x + 690 = 900 ( subtract 690 from both sides )
2x = 210 ( divide both sides by 2 )
x = 105
Select all the transformations that would carry rectangle MATH onto itself.
Aa reflection across z=-1
B a reflection across y=-1
C reflection across the x-axis
D a 90° rotation about the origin
E a 180 rotation about (0,-1)
Answers
Answer:
B and E
Step-by-step explanation:
what is the probability of rolling a six-sided die six times and having all the number 1 through 6 result (in any order)?
Answers
The probability of rolling a six-sided die six times and having all the numbers 1 through 6 result (in any order) is approximately 1.54%.
The probability of rolling a six-sided die six times and having all the numbers 1 through 6 result (in any order) can be calculated using the following steps:
1. First, find the total number of possible outcomes. Since there are 6 sides on the die and you are rolling it 6 times, there are 6^6 (or 46656) possible outcomes.
2. Next, determine the number of favorable outcomes. This is the number of ways you can arrange the numbers 1 through 6 in any order. You can do this using the formula for permutations:
n! (n factorial), where n is the number of items being arranged.
In this case, n = 6, so 6! = 6 × 5 × 4 × 3 × 2 × 1 = 720.
3. Finally, divide the number of favorable outcomes by the total number of possible outcomes to find the probability.
In this case, 720 (favorable outcomes) ÷ 46656 (total outcomes) ≈ 0.0154, or 1.54%.
So, the probability of rolling a six-sided die six times and having all the numbers 1 through 6 result (in any order) is approximately 1.54%.
for such more question on probability
https://brainly.com/question/24756209
#SPJ11
anybody help me
explain how to do it if ya can
Answers
2x3=6
2x9=18
6+18=24 square meters
Answer:
If the left side of the big rectangle is 2m then the right side should be the same. We have 4m
If the bottom of the big rectangle is 9 then the top should also be 9. We now have 22m.
-----------------------------------------------------------------------------------------------------------
SMALL RECTANGLEThe left side of the small rectangle is 2m then so should the right be also 2m. We have 4m.
The top is 3m so the bottom should also be 3m we now have 10m
----------------------------------------------------------------------------------------------------------
ANSWERIf you add 10 + 22 you get 32. 32 is your answer :)
Step-by-step explanation:
From the top of a 45 ft tower a person can see the other on the ground with an angle of depression of 40° what is the horizontal distance from the person at the base of the tower
Answers
Answer:
Step-by-step explanation:
32
I'm done with this test, just exhausted from it. Brainly do your magic.
Answers
Answer:
4.5
Step-by-step explanation:
when the height is 0 the ball will hit the ground
so the equation is
-12t²+54t=0
12t²-54t=0
2t²-9t=0
t(2t-9)=0
t=0
t=4.5
so the answer is
4.5
given a sample of four electricians, what is the standard deviation for the sampling distribution of the sample mean?
Answers
If the standard deviation is 12,000 dollars for four electricians, then the standard deviation for the sampling distribution of the sample mean is 6000 dollars.
The standard deviation of the sampling distribution of the sample mean, is also known as the standard error of the mean,
The standard deviation is be calculated using the formula,
⇒ standard-error of mean is = σ/√n,
Where σ = population standard deviation and n = sample size,
In this case, σ = 12,000 dollars and n = 4.
Substituting these values into the standard deviation formula, we get,
⇒ "standard-error" of mean = 12000/√4 = 6,000 dollars.
Therefore, the standard deviation for the sampling distribution of the sample mean is 6,000 dollars.
Learn more about Standard Deviation here
https://brainly.com/question/30260042
#SPJ4
The given question is incomplete, the complete question is
Suppose that, on average, electricians earn approximately μ = 54,000 dollars per year in the United States. Assume that the distribution for electrician's yearly earnings is normally distributed and that the standard deviation is σ = 12,000 dollars. Given a sample of four electricians,
What is the standard deviation for the sampling distribution of the sample mean?
The length of rod PR is adjusted to 16 feet. If width PQ remains the same, what is the approximate new height QR of the scaffold? Round your answer to the nearest hundredth.
Answers
Question:
Look at the picture of a scaffold used to support construction workers. The height of the scaffold can be changed by adjusting two slanting rods, one of which, labeled PR, is shown: Part A: What is the approximate length of rod PR? Round your answer to the nearest hundredth. Explain how you found your answer stating the theorem you used. Show all your work. (5 points)
B) The length of rod PR is adjusted to 16 feet. If width PQ remains the same, what is the approximate new height QR of the scaffold? Round your answer to the nearest hundredth.
Answer:
A) 16.64 Feets
B) 7.65 feets
Step-by-step explanation:
Given the following :
The question above can be solved by applying Pythagoras rule :
A^2 = B^2 + C^2
PR² = PQ² + QR²
PR² = 14² + 9²
PR² = 196 + 81
PR = √277
PR = 16.64feet
Now if PR is adjusted to 16 Feets, the New height of the scaffold will be:
QR² = PR² - PQ²
QR² = 16² - 14²
QR² = 256 - 196
QR² = 60
Take the Square root of both sides
QR = √60
QR = 7.7459666 Feets
cde=93 i dont know how but plss help
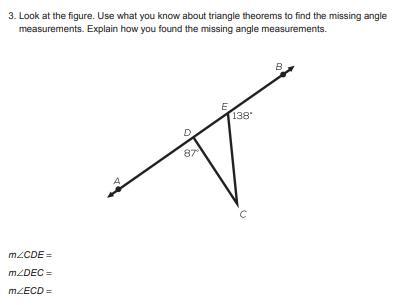
Answers
Answer:
1) 93 2) 42 3) 135
Step-by-step explanation:
Angle CDE is 93 degrees because it's a supplementary angle. A straight line is equal to 180 degrees. So, you'd just do 180-87. This same rule applies for angle DEC where 180-138 is equal to 42. Then to find angle ECD, you'd do 93+42+x=180. Since a triangle is equal to 180 degrees.
What is the length of the missing leg? If necessary, round to the nearest tenth
Answers
The value of the missing length is 48
How to determine the valueUsing the Pythagorean theorem, we have that;
a² = b² + c²
Given that the parameters are;
a is the hypotenuseb is the opposite sidec is the adjacent sideSubstitute the values, we get;
80² = 64² + c²
Find the squares
6400 - 4096 = c²
substract the values
c² = 2304
find the square root
c = 48
Hence, the value is 48
Learn about Pythagorean theorem at: https://brainly.com/question/343682
#SPJ1
The perimeter of a square is 4s, where s is the length of one side.
Find the perimeter of the square at the right. Show unit analysis.
7 ft
Answers
Answer:
28ft.
Step-by-step explanation:
If \(s\) equals 7 and the perimeter equals 4 times \(s\), then the perimeter would be 4 times 7.
Amir has 3 jars of sweets jar a contains 205 sweets jar c contains 175 sweets jar a has the most sweets and jar c has the least number of sweets how many sweets could be in jar b expain how you know this
Answers
Answer:
Step-by-step explanation:
well jar b's amount of sweets must be between 205 and 175
A shop owner needs to put 57 plants on shelves. Each shelf can hold 9 plants.
The owner uses this number sentence.
57 +9 = 613
Which statement can be used to determine the number of shelves needed?
O A. She will need 3 shelves with each shelf holding 6 plants.
B. She will need 6 shelves with each shelf holding 9 plants.
C. She will need 7 shelves with 6 shelves holding 9 plants each and 1 shelf holding 3 plants.
3
D. She will need 9 shelves with 6 shelves holding 3 plants each and 1 shelf holding 6 plants.
Answers
7
I don't know how I would explain this, sorry.
Somebody else would probably be able to explain this better than me.
Answer:
C
Explanation:
Because If it is per shelf then to find the answer you need to use multiplication.
57 divided by 9 is 6 with 3 leftover so 6 shelves can hold 54 plants equally. But since there are still plants leftover you need one more extra shelf to hold the extra 3.
If z=(x+y)ey,x=3t,y=3−t2, find dt /dz using the chain rule. Assume the variables are restricted to domains on which the functions are defined. dt /dz =
Answers
The derivative dt/dz is equal to 1 divided by the expression\([3e^(3 - t^2) - 2te^(3 - t^2)] - 2t(3t + (3 - t^2))e^(3 - t^2).\)
Starting with the expression for z, we substitute x and y with their respective expressions in terms of t:
\(z = (x + y)e^y = (3t + (3 - t^2))e^(3 - t^2).\)
Next, we need to differentiate z with respect to t to find dz/dt. Applying the chain rule, we obtain:
\(dz/dt = [(d/dt)(3t + (3 - t^2))e^(3 - t^2)] + [(3t + (3 - t^2))(d/dt)e^(3 - t^2)].\)
Taking the derivative of each term, we have:
\(dz/dt = [3e^(3 - t^2) - 2te^(3 - t^2)] + [(3t + (3 - t^2))(-2te^(3 - t^2))].\)
Simplifying this expression gives:
\(dz/dt = [3e^(3 - t^2) - 2te^(3 - t^2)] - 2t(3t + (3 - t^2))e^(3 - t^2).\)
To find dt/dz, we take the reciprocal of dz/dt:
dt/dz = 1 / dz/dt.
Therefore, \(dt/dz = 1 / [3e^(3 - t^2) - 2te^(3 - t^2)] - 2t(3t + (3 - t^2))e^(3 - t^2)\)
Learn more about chain rule here:
https://brainly.com/question/31585086
#SPJ11
Lauren did not pay her January FlashCard bill in full, so her February bill
has a finance charge added on. The average daily balance is $510.44, and the
monthly periodic rate is 1.3%. What should Lauren's finance charge be on her
February statement?
Answers
Answer:
12.76
Step-by-step explanation:
because 510.44 x 2.5%= 510.44 x 0.025= 12.76
hope this helps you guys have a great day to all of you guys
The finance charge would be the amount of $6.64 on Lauren's February statement.
What is the finance charge?
The finance charge is the multiplication of the average daily balance and the monthly periodic rate.
The finance charge = average daily balance × monthly periodic rate
The bill shows an average daily balance of $510.44, and the monthly periodic rate is 1.3%.
The finance charge = $510.44 x 1.3%.
The finance charge = $6.635
Round the nearest to the hundredth,
The finance charge = $6.64
Hence, the finance charge would be the amount of $6.64 on Lauren's February statement.
Learn more about the finance charges here:
brainly.com/question/808640
#SPJ2
Can someone help out with the optimised approach for the below problem since I got timeout issue with brute force approach
Given a range of integers determine how many numbers have no repeating digits.
Answers
The final count of integers with no repeating digits within the range is 1000 - 9 - 900 = 91.
The problem requires finding the number of integers within a range that don't contain any repeating digits. The brute force method for this would be to check every integer in the range for repeating digits, which is computationally expensive and can lead to time-out issues in certain cases.
Optimized Approach To optimize the approach, we can observe that the number of integers with no repeating digits within a range is significantly less than the number of integers with repeating digits. Therefore, instead of checking every integer for repeating digits, we can start by counting the numbers with repeating digits and then subtracting that number from the total count of integers in the range.To do this, we can use a function that checks if a given integer contains any repeating digits. If it does, then we add it to the count of numbers with repeating digits. If it doesn't, then we move on to the next integer. Once we've checked all integers in the range, we can subtract the count of numbers with repeating digits from the total count of integers in the range to get the final answer.For example, if we have a range of integers from 1 to 1000, the total count of integers in the range is 1000. We can start by checking if 11, 22, 33, ..., 99 contain repeating digits, which they do. So, we add 9 to the count of numbers with repeating digits. Then, we can check if 100, 101, 102, ..., 999 contain repeating digits, which they do as well. So, we add 900 to the count of numbers with repeating digits. Therefore, the final count of integers with no repeating digits within the range is 1000 - 9 - 900 = 91.
Learn more about Integers
brainly.com/question/15276410
#SPJ11
Please help this is due tomorrow help
Answers
Answer: $4.50
Step-by-step explanation:
6+6+3.5= 15.5 paid with a 20 so 4 dollars and 50 cents change
Answer:
Step-by-step explanation:
Since Aiden paid only the admission price not the skate rental price soo..
3.50 for himself and 6*2 =12 for his friends
3.50+12=15.50
20-15.50 = 4.50 in change :)