After completing a documentary film about the history of different font styles, the producer wonders if people will find the topic a bit boring. To measure boredom, she asks people to watch the film and then videotapes them while they are watching the film. Later, a research assistant watches the videos and records the number of times each person yarns. The data are as follows:
X F.
0 1
1 2
2 1
3 1
4 2
5 6
6 7
7 6
8 5
Compute the mean.
a. 5
b. 5.45
c. 4.5
d. 6.45
e. 6
f. 7
Answers
Answer:
\(Mean = 5.45\)
Step-by-step explanation:
Given
\(\begin{array}{cc}{x} & {f} & {0} & {1} & {1} & {2} \ \\ {3} & {1} & {4} & {2} & {5} & {6} & {6} & {7} & {7} & {6} & {8} & {5}\ \end{array}\)
Required
Calculate the mean
Mean is calculated as:
\(Mean = \frac{\sum fx}{\sum f}\)
So, we have:
\(Mean = \frac{0*1 + 1*2 + 2*1 + 3*1+4*2+5*6+6*7+7*6+8*5}{1+2+1+1+2+6+7+6+5}\)
\(Mean = \frac{169}{31}\)
\(Mean = 5.45161290323\)
\(Mean = 5.45\) -- approximated
Related Questions
The darkness of the print is measured quantitatively using an index. If the index is greater than or
equal to 2.0 then the darkness is acceptable. Anything less than 2.0 means the print is too light and
not acceptable. Assume that the machines print at an average darkness of 2.2 with a standard
deviation of 0.20.
(a) What percentage of printing jobs will be acceptable? (4)
(b) If the mean cannot be adjusted, but the standard deviation can, what must be the new standard
deviation such that a minimum of 95% of jobs will be acceptable?
Answers
84.13% of the printing jobs will be acceptable.
The new standard deviation required to achieve a minimum of 95% of jobs acceptable is 0.121.
The darkness of the print is measured quantitatively using an index. If the index is greater than or equal to 2.0 then the darkness is acceptable. Anything less than 2.0 means the print is too light and not acceptable. The machines print at an average darkness of 2.2 with a standard deviation of 0.20.
The mean of the darkness of the print is µ = 2.2 and the standard deviation is σ = 0.20.Therefore, the z-score can be calculated as; `z = (x - µ) / σ`.The index required for acceptable prints is 2.0. Thus, the percentage of prints that are acceptable can be calculated as follows;P(X ≥ 2.0) = P((X - µ)/σ ≥ (2.0 - 2.2) / 0.20)P(Z ≥ -1) = 1 - P(Z < -1)Using the standard normal table, P(Z < -1) = 0.1587P(Z ≥ -1) = 1 - 0.1587= 0.8413.
To find the new standard deviation, we can use the z-score formula.z = (x - µ) / σz = (2.0 - 2.2) / σz = -1Therefore, P(X ≥ 2.0) = 0.95P(Z ≥ -1) = 0.95P(Z < -1) = 0.05Using the standard normal table, the z-score value of -1.645 corresponds to a cumulative probability of 0.05. Hence,z = (2.0 - 2.2) / σ = -1.645σ = (2.0 - 2.2) / -1.645= 0.121.
for such more question on deviation
https://brainly.com/question/475676
#SPJ8
how oes the relationship between logarithms and exponential functions help us find solutions

Answers
The relationship between logarithms and exponential functions is fundamental and provides a powerful tool for finding solutions in various mathematical and scientific contexts.
Logarithms are the inverse functions of exponential functions. They allow us to solve equations and manipulate exponential expressions in a more manageable way. By taking the logarithm of both sides of an exponential equation, we can convert it into a linear equation, which is often easier to solve.
One of the key properties of logarithms is the ability to condense multiplication and division operations into addition and subtraction operations. For example, the logarithm of a product is equal to the sum of the logarithms, and the logarithm of a quotient is equal to the difference of the logarithms.
Logarithms also help us solve equations involving exponential growth or decay. By taking the logarithm of both sides of an exponential growth or decay equation, we can isolate the exponent and solve for the unknown variable.
This is particularly useful in fields such as finance, population modeling, and radioactive decay, where exponential functions are commonly used.
Furthermore, logarithms provide a way to express very large or very small numbers in a more manageable form. The logarithmic scale allows us to compress a wide range of values into a smaller range, making it easier to analyze and compare data.
In summary, the relationship between logarithms and exponential functions enables us to simplify and solve equations involving exponential expressions, model exponential growth or decay, and manipulate large or small numbers more effectively.
For more such question on logarithms visit:
https://brainly.com/question/25993029
#SPJ8
A submarine descended 32 feet below the surface of the ocean. It then rose 15 feet o look at a shark. Write a solution using integers and solve to find the current depth of the submarine. (Answer should be negative)
Solution and Answer:
Answers
Answer:
-32+15= -17ft
Step-by-step explanation:
when substracting integers with different signs, you substract and keep the sign of the higher number. 32-15=17 and the higher number which is 32 has a negative sign so -17.
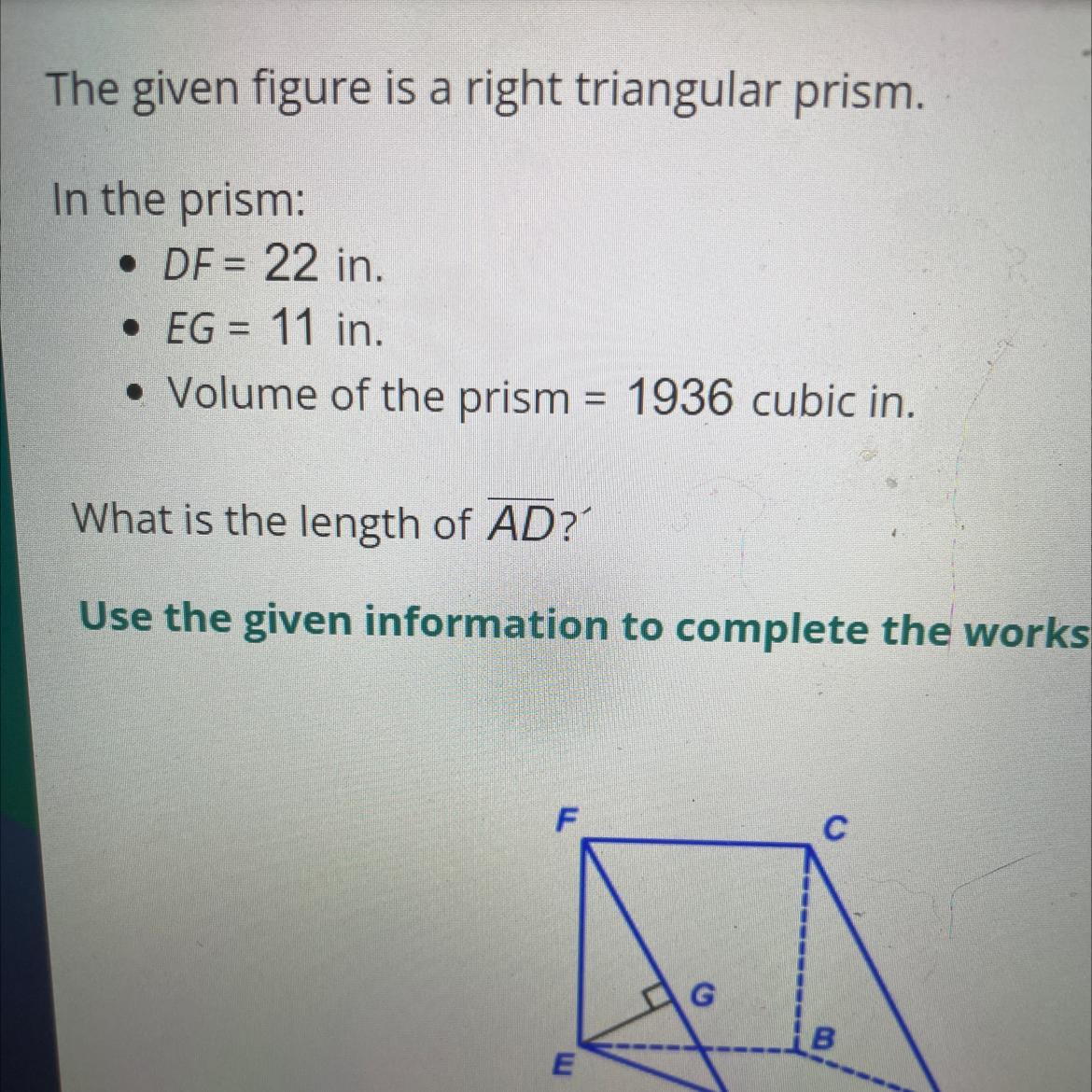
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
What is the length of AD?'
Use the given information to complete the worksheet.
Thank you!
Answers
The length of side AD is,
⇒ AD = 16
We have to given that;
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
Since, Volume of right triangular prism is,
V = 1/2 (bh) x L
Substitute all the values we get;
V = 1/2 (22 × 11) × AD
1936 = 121 × AD
AD = 16
Thus, The length of side AD is, 16
Learn more about the multiplication visit:
https://brainly.com/question/10873737
#SPJ1
Ms. Johnson had 3/4 of a tank of gas when she started a trip. When she arrived home, she had 1/8 of a tank left.What fraction of a tank of gas was used during the trip
Answers
Answer:
5/8
Step-by-step explanation:
3/4 = 6/8
6/8 - x = 1/8
x = used gas = 5/8
x is the fraction used
3/4 - 1/8 = x
(8)3/4 - 1/8(4) = x
24/32 - 4/32 = x
20/32 = x
Simplify
20/32 (/4) = 5/8
Hence she used 5/8 of the tank
To check the answer
3/4 - 5/8 = 1/8
ANSWER:
5/8
(1/5) ^ 3 * (1/5) ^ 4 * (1/5) =
Answers
9514 1404 393
Answer:
(1/5)^8
Step-by-step explanation:
The applicable rules of exponents are ...
a = a^1
(a^b)(a^c) = a^(b+c)
__
(1/5)^3 · (1/5)^4 · (1/5) = (1/5)^(3+4+1) = (1/5)^8
= 1/390625
Drag each number to a box to complete the table. Each number may be used once or not at all
Answers
Each number should be dragged to a box to complete the table as follows;
Kilometers Meters
1 1,000
2 2,000
3 3,000
5 5,000
8 8,000
What is a conversion factor?In Science and Mathematics, a conversion factor can be defined as a number that is used to convert a number in one set of units to another, either by dividing or multiplying.
Generally speaking, there are one (1) kilometer in one thousand (1,000) meters. This ultimately implies that, a proportion or ratio for the conversion of kilometer to meters would be written as follows;
Conversion:
1 kilometer = 1,000 meters
2 kilometer = 2,000 meters
3 kilometer = 3,000 meters
4 kilometer = 4,000 meters
5 kilometer = 5,000 meters
6 kilometer = 6,000 meters
7 kilometer = 7,000 meters
8 kilometer = 8,000 meters
Read more on conversion factor here: brainly.com/question/28308386
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

A figure has a area of 25 units^2. what will the new area be after a dilation with a scale factor of 5?
Answers
Answer:
625 units²
Explanation:
Given that the area of the figure = 25 square units
On dilation with a scale factor, the new area is obtained using the formula:
\(\begin{gathered} \text{New Area=Old Area}\times k^2 \\ \text{Scale Factor,}k=5 \end{gathered}\)Therefore, the new area is:
\(\begin{gathered} =25\times5^2 \\ =25\times25 \\ =625\; units^2 \end{gathered}\)The new area is 625 square units.
Suppose the population of a certain city is 5289 thousand. It is expected to decrease to 4530 thousand in 50 years. Find the percent decrease.
The percent decrease is approximately \%.
(Round to the nearest tenth.)
Answers
Answer:
14.4% decrease
Step-by-step explanation:
Here is the formula for finding the percentage of decrease:
(starting value - final value) / starting value * 100.
So for your question,
\(\frac{5289-4530}{5289} =.0144\\.0144 * 100 = 14.4\\\)/
There was a 14.4% decrease within 50 years.
Short Response What is the cost of 15 tomatoes?
HOME GROWN VEGETABLES
Cucumbers 6 for $2
Peppers 12 for $9
Tomatoes 6 for $4
Answers
Answer:
60
Step-by-step explanation:
15x4= 60
simplify the expression 5×6+6+6–12×2
Answers
Answer:
18
Step-by-step explanation:
Use PEMDAS
p=parenthesis
E=exponent
M=multiplication
D=division
A=addition
S=subtraction
PLEASE HELP!!!!!!!!!!!!!

Answers
Hope this helps!
A raffle is going to be held in which the winner will get $200. If 1000 tickets are to be sold, what is the fair
price for a ticket?
Answers
Answer:
$5
Step-by-step explanation:
1000/200=5
Answer:
20 cents.
Step-by-step explanation:
A fair price would be 200/1000 = 1/5 of a dollar which is 20 cents. But this does not allow for the people putting on the raffle to make any money for doing it. It would be better if the raffle went for a dollar. Most people would think that is fair and would not begrudge a dollar.
Select the statements which could describe the graph of a nonproportional relationship.
Answers
Answer:
what it says iiiiiiii888i888iiiii
Find the value of n for which the division of x^2n-1 by x+3 leave remainder of -80.
Answers
The value of 'n' for which the division of x^(2n-1) by x + 3 leaves a remainder of -80 is n = 1.
To find the value of 'n' for which the division of x^(2n-1) by x + 3 leaves a remainder of -80, we can use polynomial long division. Let's perform the division step by step:
Write the dividend and divisor in polynomial long division format:
_________________________
x + 3 │ x^(2n-1) + 0x^(2n-2) + 0x^(2n-3) + ...
Divide the leading term of the dividend (x^(2n-1)) by the leading term of the divisor (x). The result is x^(2n-1)/x = x^(2n-2).
Multiply the divisor (x + 3) by the quotient obtained in the previous step (x^(2n-2)). The result is x^(2n-2) * (x + 3) = x^(2n-1) + 3x^(2n-2).
Subtract the result obtained in step 3 from the original dividend:
x^(2n-1) + 0x^(2n-2) + 0x^(2n-3) + ... - (x^(2n-1) + 3x^(2n-2)) = -3x^(2n-2) + 0x^(2n-3) + ...
Bring down the next term of the dividend (which is 0x^(2n-3)) and repeat steps 2-4 until the remainder is constant.
Since we are given that the remainder is -80, we can set the remainder equal to -80 and solve for 'n'.
-3x^(2n-2) + 0x^(2n-3) + ... = -80
Since the remainder is constant (-80), it means that all the terms with x have been canceled out in the division process. Therefore, we can deduce that the highest power of x in the divisor (x + 3) is 0.
This implies that x^(2n-2) = 0, and for any value of 'n', the exponent 2n-2 should be equal to zero. Solving this equation:
2n-2 = 0
2n = 2
n = 1
Therefore, the value of 'n' for which the division of x^(2n-1) by x + 3 leaves a remainder of -80 is n = 1.
for such more question on remainder
https://brainly.com/question/825875
#SPJ8
Math homework help please

Answers
Answer:
answer is D
Step-by-step explanation:
(2^3)^-2= 2^(3)*(-2)
= 2^-6
= 1/2^6
= 1/64
The expressions (a), (d), (e) and (f) have values less 1.
What are expressions?Expressions in maths are mathematical statements that have a minimum of two terms containing numbers or variables, or both, connected by an operator in between.
Solving each expression :-
1) 4¹¹ / 4¹⁴
= 4¹¹ × 4⁻¹⁴
= (4)¹¹⁻¹⁴
= 4⁻³
= 1 / 4³
2) (3⁵)² / 3⁸
= 3¹⁰ / 3⁸
= 3¹⁰⁻⁸
= 3²
= 9
3) 4⁻¹ × 4⁵
= 4⁻¹⁺5
= 4⁴
= 64
4) (2³)⁻²
= 2⁻⁶
= 1 / 2⁶
5) (5⁴)² x 5⁻¹¹
= 5⁸ x 5⁻¹¹
= 5⁻³
= 1 / 5³
6) (6⁻⁴ x 6⁶) / 6³
= 6² / 6³
= 1 / 6
Hence, the expressions (a), (d), (e) and (f) have values less 1.
For more references on expressions, click;
https://brainly.com/question/14083225
#SPJ2
The spinner below shows
5 equally sized slices. Yolanda spun the dial
20 times and got the following results. (a) Assuming that the spinner is fair, compute the theoretical probability of landing on grey. (b) From Yolanda's results, compute the experimental probability of landing on grey. (c) Assuming that the spinner is fair, choose the statement below that is true:
As the number of spins increases, we expect the experimental and theoretical probabilities to become closer, though they might not be equal.
As the number of spins increases, we expect the experimental and theoretical probabilities to become farther apart.
The experimental and theoretical probabilities must always be equal.

Answers
A) there are 5 slices and 2 of them are grey.
The theoretical probability to land on grey would be the number of grey slices over the total number of slices: 2/5
B) the experimental probability would be the number of times the spinner landed in grey over the number of times the spinner was spun. From the table the spinner landed on grey 11 times and was spun 20 times. The experimental probability is 11/20
C) not all the answer choices are shown.
But the experimental and theoretical probabilities would most likely be different.
Answer:
From Yolanda's result, compute the experimental porbability of landing on grey
Step-by-step explanation:
What is the approximate area of a circle with a radius of 15 ft? O A. 47ft O B. 94 ft? O c. 70742 O D. 177 ft
Answers
The approximate area of a circle with radius 15 ft is given by (c) 707 sq. ft.
Area of a circle when the radius of circle is r is given by,
\(A=\pi r^2\)
Here given that the radius of circle is = 15 ft
So the value of r=15
Now the area of the circle is given by,
\(A=\pi (15)^2=225\times3.14\approx707\) square ft.
Hence the correct option is (c) 707 sq. ft
To know more about Area of circle refer to:
https://brainly.com/question/14068861
#SPJ9
Juan sold a bicycle at a discount of 15%. If the selling price was $340, find the usual price of the bicycle.
Answers
Answer: $400
Step-by-step explanation:
Discount = 15%
The original price/value of an item is always 100%
So selling price (%) = original price - discount = 100%-15% = 85%
We got selling price as 85%
This implies that 85% = 340
Let's find 1% first, then 100%
1% = 340÷85 = 4
100% = 4 × 100 = $400
The usual (normal/original) price is $400
Juan sold a bicycle at a discount of 15% if the selling price was $340 then the usual price of the bicycle was $400.
What is Percentage?percentage, a relative value indicating hundredth parts of any quantity.
Let's represent the usual price of the bicycle by P.
Since Juan sold the bicycle at a discount of 15%, the selling price (S) would be 85% of the usual price (P).
We can express this relationship as an equation:
S = 0.85P
We also know that the selling price of the bicycle was $340.
Substituting S = $340 into the equation above, we get:
$340 = 0.85P
To find P, we can solve for it:
P = $340 / 0.85
P = $400
Therefore, the usual price of the bicycle was $400.
To learn more on Percentage click:
https://brainly.com/question/24159063
#SPJ2
The diagram shows a shape made from a solid cube and a solid cylinder.
The cube has sides of length 8.7 cm.
The cylinder has a radius of 2.7 cm and a height of 4.9 cm.
Calculate the total surface area of the solid shape.
Give your answer correct to 3 significant figures.
Answers
The total surface area of the solid shape made from the cube and cylinder is approximately 583.31 cm².
How to calculate the areaThe side length of the cube is 8.7 cm, so the surface area of one face is A = 8.7²
= 75.69 cm²
Since there are six faces, the total surface area of the cube is 6 * 75.69 = 454.14 cm²
Since there are two circular bases, the total surface area of the bases is 2 * 22.91 = 45.82 cm².
In this case, the radius of the cylinder is 2.7 cm and the height is 4.9 cm, so the curved surface area is A_curved = 2 * π * 2.7 * 4.9 ≈ 83.35 cm².
Total surface area = surface area of the cube + surface area of the cylinder
Total surface area = 454.14 cm² + 45.82 cm² + 83.35 cm²
Total surface area ≈ 583.31 cm²
Learn more about area on
https://brainly.com/question/25292087
#SPJ1
PLease help, this is due tomorrow by 1 pm.

Answers
Note that the parameters of the graph a and graph b are given below.
Graph A - y=2(x-1)²
See graph attached.
Graph B - y = 1/2x² + 3
Vertex: The vertex of the function is (0, 3).
Axis of symmetry: The axis of symmetry is the vertical line passing through the vertex, which is x = 0.
Y-intercept: The y-intercept is the point where the graph intersects the y-axis. It is (0, 3).
Minimum or maximum: The coefficient of x² is positive, which means the parabola opens upwards, and therefore the function has a minimum value. The minimum value is 3.
Solutions: To find the solutions or roots of the quadratic equation, we need to set y or f(x) equal to zero and solve for x.
0 = 1/2 x² + 3
Subtracting 3 from both sides, we get:
-3 = 1/2 x²
Multiplying both sides by -2, we get:
6 = -x²
Taking the square root of both sides, we get:
x = ±√(-6)
Since the square root of a negative number is not a real number, the function has no real roots.
Minimum or maximum value: The minimum value of the function is 3.
Range: The range of the function is y ≥ 3, because the function has a minimum value of 3.
Domain: The domain of the function is all real numbers, because there are no restrictions on the values of x for which the function is defined.
Stretch/Shrink/Standard: The coefficient of x^2 is positive and less than 1, which means that the graph of the function is narrower than the graph of y = x². This is an example of a standard quadratic function that has been vertically compressed by a factor of 1/2.
See graph attached.
Learn more about graphs at:
https://brainly.com/question/17267403
#SPJ1


Find the slope of the line parallel to the line graphed.
My Answer:

Answers
A Fair Isaac Corporation (FICO) score is used by credit agencies (such as mortgage companies and banks) to assess the creditworthiness of individuals. Values range from 300 to 850, with a FICO score over 700 considered to be a quality credit risk. According to Fair Isaac Corporation, the mean FICO score is 703.5. A credit analyst wondered whether high-income individuals (incomes in excess of $100,000 per year) had higher credit scores. He obtained a random sample of 40 high-income individuals and found the sample mean credit score to be 714.2 with a standard deviation of 83.2. Conduct the appropriate test to determine if high-income individuals have higher FICO scores at the \alpha=0.05α=0.05 level of significance.
Answers
Solution :
Given :
Sample mean, \($\overline x = 714.2$\)
Sample size, n = 40
Standard deviation, s = 83.2
∴ The null hypothesis is \($H_0 : \mu = 703.5$\)
Alternate hypothesis is \($H_a : \mu > 703.5$\)
Test statistic :
\($z = \frac{\overline x - \mu}{s / \sqrt n}$\)
\($z = \frac{714.2-703.5}{83.2 / \sqrt {40}}$\)
z = 0.813
Now at α = 0.05, for a right tailed,
\($z_{critical} = 1.645$\)
Since, \($z < z_{critical}$\) , we fail to reject the null hypothesis.
This graph shows how fast a commuter train travels on its route in an urban area. What is the meaning of the point with an x-coordinate of 4
Answers
The meaning of the point with an x-coordinate of 2 is in 2 seconds, the commuter travels 120 feet.
What is an equation?An equation is an expression that shows the relationship between two or more numbers and variables.
Independent variables represent function inputs that do not depend on other values, while dependent variables represent function outputs that depends on other values.
From the graph, the x coordinate 2, have a y coordinate of 120. Hence:
The meaning of the point with an x-coordinate of 2 is in 2 seconds, the commuter travels 120 feet.
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1

The quotient of two numbers is 3 their difference is 8 what are the two numbers
Answers
Answer:
x = 12, y = 4
Step-by-step explanation:
x / y = 3
x - y = 8
Or
12 / 4 = 3
12 - 3 = 8
In a poll of 1556 registered voters nationwide, 43% of those polled blamed oil companies the most for the recent increase in gasoline prices. Test the claim that the percentage of registered voters nationwide who blame oil companies the most for the recent increase in gasoline prices is at least 45% using alpha = 0.01. Test statistic z = -1.59. P-Value = 0.94 A. Since the P-value > alpha, we cannot conclude that the percentage of registered voters nationwide who blame oil companies the most for the recent increase in gasoline prices is at least 45%. B. Since the P-value is larger than 45%, we cannot conclude that the percentage of registered voters nationwide who blame oil companies the most for the recent increase in gasoline prices is at least 45%. C. Since the P-value > alpha, we can conclude that the percentage of registered voters nationwide who blame oil companies the most for the recent increase in gasoline prices is at least 45%. D. Since the P-value > alpha, we conclude that the percentage of registered voters nationwide who blame oil companies the most for the recent increase in gasoline prices is 45%. E. Since the P-value > alpha, we conclude that the percentage of registered voters nationwide who blame oil companies the most for the recent increase in gasoline prices is 43%.
Answers
A poll of 1556 registered voters nationwide indicated that 43% of those polled blamed oil companies the most for the recent increase in gasoline prices. Therefore, option A is correct: Since the P-value > alpha, we cannot conclude that the percentage of registered voters nationwide who blame oil companies the most for the recent increase in gasoline prices is at least 45%.
To determine whether this poll result supports the claim that at least 45% of registered voters blame oil companies the most for the recent increase in gasoline prices, we test the null hypothesis against the alternative hypothesis.
Test the claim that the percentage of registered voters nationwide who blame oil companies the most for the recent increase in gasoline prices is at least 45% using alpha = 0.01. Test statistic z = -1.59. P-Value = 0.94.
Since the P-value > alpha, we cannot conclude that the percentage of registered voters nationwide who blame oil companies the most for the recent increase in gasoline prices is at least 45%.
Therefore, option A is correct: Since the P-value > alpha, we cannot conclude that the percentage of registered voters nationwide who blame oil companies the most for the recent increase in gasoline prices is at least 45%.
for such more question on indicated
https://brainly.com/question/29021083
#SPJ11
Nine busses of students, teachers, and parents went on a field trip. If 5 of the buses held 63 people each and the other buses held 54 people each, how many people went in all?
Answers
An expression is a way of writing a statement with more than two variables or numbers with operations such as addition, subtraction, multiplication, and division.
The total number of people want in all is 531.
What is an expression?An expression is a way of writing a statement with more than two variables or numbers with operations such as addition, subtraction, multiplication, and division.
Example: 2 + 3x + 4y = 7 is an expression.
We have,
Number of buses = 9
Number of buses that has 63 people = 5
Number of buses that has 54 people = 4
The total number of people in all the buses.
= 5 x 63 + 4 x 54
= 315 + 216
= 531
Thus,
The total number of people want in all is 531.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
a car travels 55 miles per hour for 2 hours. How far did it travel in 1 1/2 hours
Answers
Answer:
82.5 miles in 1 1/2 hours
Step-by-step explanation:
Using the information the question gives us we can find the appropriate answer to this question by dividing the miles per hour by two, and then add that number to the additional miles per hour.
55 miles = one hour
2 hours = 110 miles
1 1/2 hours = 55 ÷ 2 = 27.5
55 + 27.5 = 82.5 miles
82.5 miles
Hope this helps
an investment had return of 13% if inflation was 4.1% what was your real return ?
Answers
Answer: 8.9%
Step-by-step explanation: 13 - 4.1
(a) Find a vector parallel to the line of intersection of the planes −4x+2y−z=1 and 3x−2y+2z=1.
v⃗ =
(b) Show that the point (−1,−1,1) lies on both planes. Then find a vector parametric equation for the line of intersection.
r⃗ (t)=

Answers
Find the intersection of the two planes. Do this by solving for z in terms of x and y ; then solve for y in terms of x ; then again for z but only in terms of x.
-4x + 2y - z = 1 ==> z = -4x + 2y - 1
3x - 2y + 2z = 1 ==> z = (1 - 3x + 2y)/2
==> -4x + 2y - 1 = (1 - 3x + 2y)/2
==> -8x + 4y - 2 = 1 - 3x + 2y
==> -5x + 2y = 3
==> y = (3 + 5x)/2
==> z = -4x + 2 (3 + 5x)/2 - 1 = x + 2
So if we take x = t, the line of intersection is parameterized by
r(t) = ⟨t, (3 + 5t )/2, 2 + t⟩
Just to not have to work with fractions, scale this by a factor of 2, so that
r(t) = ⟨2t, 3 + 5t, 4 + 2t⟩
(a) The tangent vector to r(t) is parallel to this line, so you can use
v = dr/dt = d/dt ⟨2t, 3 + 5t, 4 + 2t⟩ = ⟨2, 5, 2⟩
or any scalar multiple of this.
(b) (-1, -1, 1) indeed lies in both planes. Plug in x = -1, y = 1, and z = 1 to both plane equations to see this for yourself. We already found the parameterization for the intersection,
r(t) = ⟨2t, 3 + 5t, 4 + 2t⟩