AABC and AXYZ are similar triangles. The lengths of two sides of each triangle are shown. Find the lengths of the third side of each triangle. 6.5 C Provide your answer below: یز چز لئے A 12 B
Answers
According to the definition of similar triangles, the corresponding sides of the triangles are in the same ratio. That is, if AABC and AXYZ are similar triangles, then the ratio of the corresponding sides will be equal.
Therefore, we can use this concept to find the lengths of the third side of each triangle.Given:AABC and AXYZ are similar triangles.The lengths of two sides of each triangle are shown.6.5 CTo find:
The lengths of the third side of each triangle.Solution:Let's use the ratio of the corresponding sides to find the lengths of the third side of each triangle.According to the ratio of the corresponding sides, we can write: AB/XY
= BC/YZ
= AC/XZ
Here, we have the length of two sides of each triangle.
So, we can use them to find the lengths of the third side.Using the ratio, we can write: AB/XY = BC/YZ
=> 12/5 = 6.5/YZ
Cross-multiplying, we get: YZ = 6.5 × 5/12
= 2.7083 (approx)
Therefore, the length of the third side of triangle AXYZ is 2.7083 (approx).
Similarly, using the ratio, we can write: AB/XY = AC/XZ
=> 12/5 = 6.5/XZ
Cross-multiplying, we get: XZ = 6.5 × 5/12
= 2.7083 (approx)
Therefore, the length of the third side of triangle AABC is 2.7083 (approx).
Hence, the required lengths of the third side of each triangle are 2.7083 (approx).
To know more about triangle visit :-
https://brainly.com/question/1058720
#SPJ11
Related Questions
Twelve less than the product of three and a number is less than 21
Answers
Answer:
11
Step-by-step explanation:
3 times 11 gives you 33 which would be the product
3 x 11 = 33
subtract the 12(twelve) from the 33(product)
33 - 12 = 21
The relationship between chocolate sales and student happiness can be tested using the ______. Group of answer choices p statistic mean difference t statistic error difference
Answers
The relationship between chocolate sales and student happiness can be tested using the mean difference.
Specifically, a statistical test such as a correlation analysis or regression analysis can be used to examine the relationship between the amount of chocolate sales and the level of student happiness.
The mean difference refers to the difference in the average level of student happiness between two groups, such as those who consume more chocolate and those who consume less chocolate. This can help determine if there is a significant association between chocolate consumption and student happiness.
To learn more about statistics here
https://brainly.com/question/15525560
#SPJ4
When describing categorical data, you can use: counts and proportions measures of center, spread, and shape All of these statements are correct. box plot None of these statements are correct.
Answers
All of these statements are correct.
When describing categorical data, several methods can be used to provide meaningful insights and summarize the data.
Counts and proportions: Counting the number of observations in each category can provide information about the distribution and frequency of different categories. Proportions, also known as percentages, can be calculated by dividing the count in each category by the total count, allowing for a comparison of the relative frequencies of different categories.
Measures of center, spread, and shape: Although measures of center, spread, and shape are commonly associated with numerical data, they can also be used to describe certain aspects of categorical data. For example, the mode represents the most frequent category, which can be considered a measure of center. Measures of spread, such as the range or interquartile range, may not be applicable to categorical data. However, bar graphs and pie charts can visually depict the distribution and shape of categorical variables.
Box plots: Box plots are graphical representations primarily used for numerical data. They display the median, quartiles, and any potential outliers. While box plots are not commonly used for categorical data, they can be adapted by representing the frequency or proportion of categories instead of numerical values.
In summary, when describing categorical data, counts and proportions are commonly used to present the frequency and relative frequency of categories. Measures of center, such as the mode, can provide insights into the most frequent category. Measures of spread and shape may not be applicable, but graphical representations like bar graphs and pie charts can be used to visualize the distribution and shape of the categorical data. Box plots are not typically used for categorical data, as they are more suitable for numerical variables.
Learn more about numerical variables here:
brainly.com/question/30527805
#SPJ11
Please help!! I will mark you brainlist!

Answers
Answer:
Step-by-step explanation:
The answer is D because all you need to do is multiply everything by 0.5, or one half.
help me!!Write a function using correct notation that models the value of each car.

Answers
Answer:
\(f(x) = 2000 * 1.05^x\)
Step-by-step explanation:
The key to this question is interpreting the graph and then modelling it into an exponential function.
You are given 2 key characteristics of this graph. 1 characteristic being that it intercepts the y-axis at (0,2000), and another characteristic being that it goes through the point (1,2100)
Now refer to the standard form of an exponential function.
\(y = a * b^x\)
Since you know that when x = 0, y = 2000, a must be 2000. Because \(b^0 = 1\), 2000 * 1 = 2000
So you got your a value. Sub it into the equation and now you got.
\(y = 2000 * b^x\)
You still need to solve for b, so this is where you do some algebra. Pick your key point, (1,2100), sub in those values for x and y, and solve for b.
\(2100 = 2000 * b^1\\\frac{2100}{2000} = b\\ 1.05 = b\)
Now you have your a and b values. Now you can express using a function:
\(f(x) = 2000 * 1.05^x\)
the gram-schmidt process produces from a linearly independent set {x1, x2, . . . , xp} an orthogonal set {v1, v2, . . . , vp} with the property that span{v1, . . . , vk}
Answers
The statement is true.
An orthogonal set with the same dimension as the initial collection of vectors is created by the Gram-Schmidt process.
Given that,
From a linearly independent collection of {x₁, x₂,..., xp}, the gram-Schmidt process creates an orthogonal set of {v₁, v₂,..., vp} with the feature that for each k, the vectors v₁...vk span the same subspace as that spanned by x₁...xk.
Whether the claim is true or false must be determined.
The statement is true.
An orthogonal set with the same dimension as the initial collection of vectors is created by the Gram-Schmidt process. An orthogonal set is further linearly independent. The orthogonal set produced by the Gram-Schmidt process and the original set will cover the same subspace if their dimensions are the same.
To learn more about orthogonal visit: https://brainly.com/question/2292926
#SPJ4
length=9in width=2in height=3in. what is the surface area
Answers
Answer:
102in2
Step-by-step explanation:
The formula for surface area is 2(wl+hl+hw). So plug in the measurements of the prism into the formula to get 102.
Find the volume of a cylinder with a diameter of 14mm and a height of 3.4mm Round to the nearest tenth.
Answers
Answer:
V≈5.23×10-7m³
Step-by-step explanation:
V=π(d
2)2h=π·(0.014
2)2·3.4×10-3≈5.23389×10-7m³
Answer: 523.1 mm^2
You first want to find the radius for the volume of cylinder formula. You first do 14 divided by 2 to get the radius. You should get 7. Then after you find the radius you then put it into the formula which is v=3.14 x radius^2 x height. The equation with all the numbers from the problem is 3.14 x 7^2 x 3.4. After you put the equation into your calculator you should get 523.1 mm^2.
Suppose that a phone originally sold for $800 loses 3/5 of its value each year after it is released. After 2 years, how much is the phone worth?A. $800B. $1333C. $128D. $288
Answers
The phone is worth $128 after 2 years, which is option C.
What is exponential decay ?
Exponential decay is a decrease in a quantity over time where the rate of decay is proportional to the current value. In this case, the value of the phone decreases by 3/5 each year after it is released. This means that the value after one year is 2/5 of the original value, and the value after two years is (2/5) times (2/5) of the original value. Exponential decay is a common phenomenon in many areas of science and mathematics, including radioactive decay, population growth and decay, and financial investments.
Calculating the worth of the phone :
The phone is not worth the same amount after 2 years, as it loses 3/5 of its value each year. We need to calculate its worth after 2 years.
Let's use the formula for exponential decay: \(A = A_0(1 - r)^t\), where A is the final amount, \(A_0\) is the initial amount, r is the decay rate, and t is the time elapsed.
In this case, the initial amount is $800, the decay rate is 3/5, and the time elapsed is 2 years. Substituting these values into the formula, we get:
\(A = 800(1 - 3/5)^2\)
\(A = 800(2/5)^2\)
\(A = 800(4/25)\)
\(A = 128\)
Therefore, the phone is worth $128 after 2 years, which is option C.
To know more about exponential decay visit :
brainly.com/question/2193799
#SPJ1
BESTIE HELP FAST !!
Which is a graph of y=-3x + 2?

Answers
Answer:
Step-by-step explanation:
it's this one
Water flows through a pipe at a rate of 620 gallons every 5.5 minutes. Express this rate of flow in cups per second.
Answers
Answer: 16 cups per second.
Step-by-step 5.5 minutes into seconds 320.
620 gallons into cups 9920.
9920 divided by 320 seconds.
16 cups per second
Kristen's financial advisor has given her a list of 8 potential investments and has asked her to select and rank her favorite four. In how many different ways can she do this?
Answers
The number of ways in which Kristen can rank her favorite four from 8 using permutations is 1680.
The permutation is a way of finding the number of ways of selecting a set of articles from a larger set of articles, with the order of selection being significant.
If we want to choose r items from n items, where the order of selection is significant, then we can find the number of ways of doing this using the permutation as follows:
nPr = n!/{(n - r)!}.
In the question, we are asked to find the number of ways Kristen can rank her favorite four investments from the 8 potential investments that her financial advisor has given her.
Thus, using permutations, we need to select 4 items from 8 items, with order of selection being significant.
Substituting n = 8, and r = 4 in the formula, we get:
8P4 = 8!/{(8 - 4)!}
= 8!/4!
= 5 * 6 * 7 * 8
= 1680.
Thus, the number of ways in which Kristen can rank her favorite four from 8 using permutations is 1680.
Learn more about permutations at
https://brainly.com/question/12468032
#SPJ4
is the sequence geometric? if so what is the common ratio/answers 2,-4,-16,-36/
Answers
Answer:
We conclude that the sequence 2, -4, -16, -36,... is not a geometric sequence.
Step-by-step explanation:
Given the sequence
2, -4, -16, -36,...
A geometric sequence has a constant ratio 'r'.Let us compute the ratio of all the adjacent terms
\(\frac{-4}{2}=-2,\:\quad \frac{-16}{-4}=4,\:\quad \frac{-36}{-16}=2.25\)
It is clear that the ratio is not constant.
Thus, the given sequence is not a geometric sequence.
Therefore, we conclude that the sequence 2, -4, -16, -36,... is not a geometric sequence.
in 2022, a study at petit pediatrics found that 10% of its patients were allergic to pollen. the study also showed that 10% of patients who were allergic to pollen tested negative, while 20% of the patients who were not allergic tested positive. if a patient is randomly selected and is not allergic to pollen, what is the probability that they tested negative? 0.90 0.80 0.72 0.10
Answers
The probability that a patient, randomly selected and not allergic to pollen, tested negative is 0.90.
To find the probability that a patient tested negative given that they are not allergic to pollen, we can use Bayes' theorem:
P(N|A complement) = [P(N complement|A complement) × P(A complement)] / P(N complement)
We know that P(A complement) = 1 - P(A) = 1 - 0.10 = 0.90. Additionally, P(N complement) can be calculated as:
P(N complement) = P(N complement|A) × P(A) + P(N complement|A complement) × P(A complement)
= 0.10 × 0.10 + 0.20 × 0.90
= 0.01 + 0.18
= 0.19
Substituting these values into the formula, we have:
P(N|A complement) = (0.20 × 0.90) / 0.19 = 0.90
Learn more about Bayes' theorem here:
https://brainly.com/question/31084060
#SPJ11
For questions 10-15. dentify the domain and range
10
Domain ? Range?
11. Domain? Range?

Answers
Answer:
See below for answers and explanations
Step-by-step explanation:
10) The domain is (-∞,+∞) because no matter what x is, it is defined for all real numbers. The range is (-∞,3] because if y is greater than 3, then no x-value can be defined for that.
11) The domain would be (−∞,3)∪(3,∞) because of the vertical asymptote located at x=3 which means x can be any real number other than 3. The range is (-∞,0)∪(0,∞) because of the horizontal asymptote located at y=0, which means y can be any real number other than 0.
pls help! brainliest promises! easy 6th grade stuff! im on my sisters acc! this is very important to my grade

Answers
Answer:
D
Step-by-step explanation:
its D trust
points x(6, 8), y(3, 3), and z(13, –3) form the triangular outline of a park. what is the area of △xyz?
Answers
Answer:
34 square units
Step-by-step explanation:
You want the area of the triangle with vertices X(6, 8), Y(3, 3), and Z(13, -3).
Area from verticesThere are several ways the area of a triangle can be calculated from the coordinates of the vertices. One relatively easy method is to find half the absolute value of the sum of the determinants of adjacent pairs of points.
This calculation is shown in the second attachment.
The area of ∆XYZ is 34 square units.
Right triangleA slope calculation will tell you side XY is perpendicular to side YZ. This means you can find the area from the lengths of these two sides. The distance formula can tell you the lengths.
XY = √((3 -6)² +(3 -8)²) = √(9 +25) = √34
YZ = √((13 -3)² +(-3 -3)²) = √(100 +36) = 2√34
Area = 1/2bh = (1/2)(√34)(2√34) = 34 . . . . square units
Pick's theoremPick's theorem tells you the area of a polygon with vertices on grid points can be found by counting the grid points on the boundary and interior to the boundary.
A = i + (b/2) -1
This triangle has the three given vertices on grid points, along with point (8, 0), which is the midpoint of YZ. There are 33 interior points, so the area is ...
A = 33 +(4/2) -1 = 34 . . . . square units
Heron's formulaThe length of XZ is ...
XZ = √((13 -6)² +(-3 -8)²) = √(49 +121) = √170
Heron's formula tells you the area is given by ...
A = √(s(s -a)(s -b)(s -c)) . . . . . . where s = (a+b+c)/2, the semiperimeter
The third attachment shows this calculation gives an area of 34 square units.
__
Additional comments
The slope calculation tells you the slope of XY is ...
m = (y2 -y1)/(x2 -x1) = -5/-3 = 5/3
and the slope of YZ is ...
m = -6/10 = -3/5 . . . . . . . . the opposite reciprocal of the slope of XY
Hence these sides are perpendicular, as we noted above.
We like Pick's theorem for finding the areas of small figures with irrational side lengths (such as this one). It just involves counting, which is often easier than using a bunch of different formulas for slope or length.
The determinant formula is easy to compute, but tedious to enter on a calculator. It is much easier to program a spreadsheet for this. As with Pick's theorem, the method applies to a polygon with any number of vertices.
\(\left|\begin{array}{cc}a&b\\c&d\end{array}\right|=ad-bc\)
In these 2×2 matrices, the coordinates can be listed in rows or in columns. It makes no difference to the calculation. The key is to work in one direction around the figure. (Here, we went CCW.)
The triangle is drawn in the first attachment. The geometry program that drew it also calculated its area to be 34 square units.
You may have noticed that the "determinant" method and Pick's theorem guarantee that the area of any polygon with integer coordinates will be an integer multiple of 1/2 square unit. That is, it will never be irrational. (You might not see that using Heron's formula.)
#95141404393



Solve the equation lol 54x+6x-30=7(x+2)+3x
Answers
Answer: 22/25
Step-by-step explanation:
54x+6x-30=7(x+2)+3x
60x-30=7(x+2)+3x
60x-30=7x+14+3x
60x-30=10x+14
60x-10x-30=14
60x-10x=14+30
50x=14+30
50x=44
x=22/25
solve the equation 16x+9=9y-2x for y.
Answers
GIVEN:
We are given the following equation;
\(16x+9=9y-2x\)Required;
Solve the equation for y.
Step-by-step solution;
To solve, we simply collect like terms as follows;
\(\begin{gathered} Add\text{ }2x\text{ }to\text{ }both\text{ }sides: \\ 16x+2x+9=9y-2x+2x \end{gathered}\)We now have;
\(18x+9=9y\)Observe that -2x and +2x cancel out each other on the right hand side.
Next step, we divide both sides by 9, that is the coefficient of y.
\(\frac{18x+9}{9}=\frac{9y}{9}\)\(\frac{18x+9}{9}=y\)Note that we can split up the left hand side. We do this by taking both numbers in the numerator and writing each as a fraction with 9 as the denominator. This is because 9 is the LCM of both fractions as it is expressed above.
We now have;
\(\frac{18x}{9}+\frac{9}{9}=y\)Now we divide both fractions by any common factors;
\(2x+1=y\)Therefore,
ANSWER:
\(y=2x+1\)a) How many different outcomes are possible when a pair of dice, one red and one white, are rolled two successive times? (b) What is the probability that each die shows the same value on the second roll as on the first roll? (c) What is the probability that the sum of the two dice is the same on both rolls? (d) What is the probability that the sum of the two dice is greater on the second roll?
Answers
a) Different outcomes possible when a pair of dice are rolled two successive times is 36. (b) The probability that each die shows the same value on the second roll as on the first roll is 1/36. (c) The probability that the sum of the two dice is the same on both rolls is 1/6. (d) The probability that the sum of the two dice is greater on the second roll is 5/12.
a) There are 36 different outcomes possible when a pair of dice, one red and one white, are rolled two successive times. This is because there are 6 possible outcomes for each die, and there are two dice, so 6 x 6 = 36 different outcomes.
b) The probability that each die shows the same value on the second roll as on the first roll is 1/36. This is because there is only one outcome out of the 36 possible outcomes that will result in both dice showing the same value on both rolls.
c) The probability that the sum of the two dice is the same on both rolls is 6/36, or 1/6. This is because there are 6 possible sums (2, 3, 4, 5, 6, 7) that can be rolled on both dice, and each of these sums has a 1/6 chance of occurring on both rolls.
d) The probability that the sum of the two dice is greater on the second roll is 15/36, or 5/12. This is because there are 15 possible outcomes where the sum of the two dice is greater on the second roll (3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17), and each of these outcomes has a 1/36 chance of occurring, so 15 x 1/36 = 15/36, or 5/12.
Learn more about Probability:
https://brainly.com/question/23955312
#SPJ11
Match the inequality to its representation on a number line.
2. Write an inequality statement whose solution is an empty set.
6. Write an inequality statement to represent the graph shown.
en inequality statement to represent the graph shown.
4. Write an inequality statement whose solution is all real numbers. Graph the solution on a number line.
3. Write an inequality statement whose solution is some but not all real numbers. Graph the solution on a number line
9
Write an inequality statement whose solution is exactly one number. Graph the solution on a number line.

Answers
An inequality depicts the relationship between two values in an algebraic statement that are not equal.
What is an inequality statement ?Inequality, a declaration of the relation of greater, greater than or equal to, smaller, or less than or equal to between two numbers or algebraic expressions.
An inequality is a claim that demonstrates the connection between two (or more) expressions that have one of the following five signs:,, >,,. Similar to an equation, an inequality can be true or untrue. A true statement is: 34 - 12 > 5 + 2. An incorrect statement is 1 + 3 6 - 2.
When two values in an algebraic expression are not equal, an inequality illustrates their relationship. One of the two variables on the two sides of the inequality can be represented by an inequality sign as greater than, greater than or equal to, less than, or equal to another value.
To learn more about inequality statement refer to:
https://brainly.com/question/30238773
#SPJ1
Find the roots of the equation: (5.1) z 4
+16=0 and z 3
−27=0 (5.2) Additional Exercises for practice are given below. Find the roots of (a) z 8
−16i=0 (b) z 8
+16i=0
Answers
Given equations are (5.1) z 4 +16=0 and z 3 −27=0.(5.1) z 4 +16=0z⁴ = -16z = 2 * √2 * i, 2 * (-√2 * i), -2 * √2 * i, -2 * (-√2 * i)Therefore, the roots of the equation are z = 2^(3/4) * i, 2^(1/4) * i, -2^(3/4) * i, -2^(1/4) * i.(5.2) z 8 −16i=0z⁸ = 16i z = 2^(1/8) * i, 2^(3/8) * i, 2^(5/8) * i, 2^(7/8) * i, -2^(1/8) * i, -2^(3/8) * i, -2^(5/8) * i, -2^(7/8) * i
Therefore, the roots of the equation are:
z = 2^(1/8) * i, 2^(3/8) * i, 2^(5/8) * i, 2^(7/8) * i, -2^(1/8) * i, -2^(3/8) * i, -2^(5/8) * i, -2^(7/8) * i. z 8 +16i=0z⁸ = -16i z = 2^(1/8) * i, 2^(3/8) * i, 2^(5/8) * i, 2^(7/8) * i, -2^(1/8) * i, -2^(3/8) * i, -2^(5/8) * i, -2^(7/8) * i
Therefore, the roots of the equation are:
z = 2^(1/8) * i, 2^(3/8) * i, 2^(5/8) * i, 2^(7/8) * i, -2^(1/8) * i, -2^(3/8) * i, -2^(5/8) * i, -2^(7/8) * i.
First of all, we need to know that a polynomial equation of degree n has n roots and they may be real or imaginary. Roots are also known as zeros or solutions of the equation.If the degree of the polynomial is n, then it can be written as an nth degree product of the linear factors, z-a, where a is the zero of the polynomial equation, and z is any complex number. Therefore, the nth degree polynomial can be factored into the product of n such linear factors, which are known as the roots or zeros of the polynomial.In the given equations, we need to find the roots of each equation. In the first equation (5.1), we have z⁴ = -16 and z³ = 27. Therefore, the roots of the equation:
z⁴ + 16 = 0 are:
z = 2^(3/4) * i, 2^(1/4) * i, -2^(3/4) * i, -2^(1/4) * i.
The roots of the equation z³ - 27 = 0 are:
z = 3, -1.5 + (3^(1/2))/2 * i, -1.5 - (3^(1/2))/2 * i.
In the second equation (5.2), we need to find the roots of the equation z⁸ = 16i and z⁸ = -16i. Therefore, the roots of the equation z⁸ - 16i = 0 are:
z = 2^(1/8) * i, 2^(3/8) * i, 2^(5/8) * i, 2^(7/8) * i, -2^(1/8) * i, -2^(3/8) * i, -2^(5/8) * i, -2^(7/8) * i.
The roots of the equation z⁸ + 16i = 0 are also the same.
Thus, we can find the roots of polynomial equations by factoring them into linear factors. The roots may be real or imaginary, and they can be found by solving the polynomial equation.
To learn more about linear factors visit:
brainly.com/question/28969245
#SPJ11
ASAP PLS! 7. Which triangles are congruent by ASA?
Choices:
O ΔABC and ΔTUV
O ΔVTU and ΔABC
O ΔVTU and ΔHGF
O none of the above
Please help with this ASAP! Best answer is rewarded with 5 stars, Thanks and Brainliest!

Answers
Five less than the product of 9 and a number x is 546
Answers
Answer:
9x-5=546
Step-by-step explanation:
9x-5=546
9x=551
x=61.22222222
highschool math. this one is pretty easy.
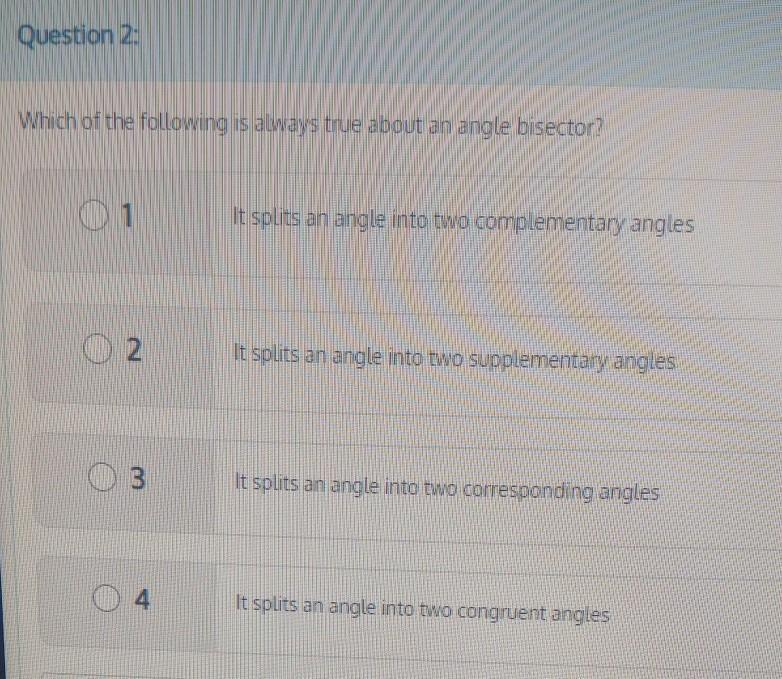
Answers
A bisector splits an angle into two equal angles.
The answer is the last one: it splits the angle into two congruent angles.
At Bell High School, 43% of the students own a CD player and 28 % own a CD player and an MP3 player. What is the probability that a student owns an MP3 player if he or she also owns a CD player?
Answers
According to the question, Let us assume the total number of students is \(100\). In which \(43\) students own a CD player. And \(28\) students own both CD player as well as MP3 Player.
Now, to calculate the probability that a student owns an MP3 player and also they own a CD player. It is clear from the given data, the percentage is higher than \(28\) percent.
Using conditional probability rule:
\(P(MP3|CD) = \frac{P(MP3 and CD)}{P(CD)} = \frac{0.28}{0.43} = 0.65\)
What is Probability?
The term probability means the study of the occurrence or the outcomes of the event. It is the measurement of the events that occurred during events. And many uncertain events cannot be measured.
To learn more about the Probability from the given link:
https://brainly.com/question/13604758
#SPJ4
A recent survey at a local company showed that 300 employees, or 66⅔% of the company’s employees, carpool to work each day. How many employees work at this company?
I'm sorry for all this trouble just really need help I'm in summer school because I was gone most of the school year and its all online so i don't understand anything
Answers
Answer:
450 employees work at this company.
Step-by-step explanation:
300 = 2/3 of x
300 × 3 = 2x
900 = 2x
450 = x
whta 250 divided by 10
Answers
Answer:
the answer would be 25
Step-by-step explanation:
10 goes in to 250 25 times
The correct answer for the value of division of 250 by 10 is 25.
What is Division?
Division involves splitting a number or quantity into equal parts or groups. it is a mathematical operation.
When the division of one number (the dividend) by another number (the divisor) is performed, the results determined how many times the divisor can fit into the dividend.
quotient is the result of division.
Signs that used to indicate division are ÷ and /.
In the given question \(250\) is divided by \(10\) , which is expressed as \(250\) ÷ \(10\)
or \(\dfrac{250}{10}\).
\(\dfrac{250}{10} = 25\).
The Quotient for the division of 250 divide by 10 is 25.
Learn more about division here:
https://brainly.com/question/19014262
#SPJ6
I dont understand how to do it someone pls help me

Answers
Answer: -3/4 and 4/3
Step-by-step explanation:
Consider the set X of all sets of exactly three integers. Select all true statements about the set X. Select one or more: a. X is uncountable b. [X] = [N], where N denotes the natural numbers c. X is countably infinite d. X is finite e. X is infinite
Answers
The correct statements about the set X of all sets of exactly three integers are:
c. X is countably infinite
e. X is infinite
How can we determine the nature of the set X?To determine the nature of the set X, we can analyze its cardinality and structure. By investigating whether X is countable or uncountable, finite or infinite, we can gain insights into the properties and size of the set.
The set X is countably infinite because it can be put into a one-to-one correspondence with the set of natural numbers (N). Each set in X can be associated with a unique natural number by ordering the integers within the set.X is infinite since there is an infinite number of sets that can be formed by selecting three integers, allowing for various combinations and repetitions.X is not uncountable as it can be enumerated and put into a countable sequence.X is not finite because there are infinitely many sets that can be formed by selecting three integers.Therefore, the correct statements about the set X of all sets of exactly three integers are:
c. X is countably infinite
e. X is infinite
To learn more about the nature of the set from the given link
brainly.com/question/27557796
#SPJ4