A. What is the average rate of change of the function g(x) = 2x - 7 between the points (-2, -11) and (5, 3)? _________ B. Use the following graphs to answer this part: - which of the above graphs is the graph of g(x)? ______ - over what intervals is g(x) increasing? ________ -- over what intervals is g(x) decreasing? ________

Answers
Part A.
To find the average rate of change, we must divide the change in y-values by the change in x-values. Then, by means of the given points, we have
\(\text{ rate of change: }\frac{y_2-y_1}{x_2-x_1}=\frac{3-(-11)}{5-(-2)}=\frac{14}{7}=2\)as we can note the rate of change must be equal to the slope of the given line equation, which is the coefficient of the variable x.
Part B
Lets graph the given equation.
By comparing with the given options, the answer is option C.
On the other hand, the function g(x) is defined for all real numbers, then (as we can see on the picture) function is increasing over all real numvbers. Then, the function increases on the interval:
\(x\in(-\infty,\infty)\)The behavior of a line is always the same, this means that the function never decreases. Therefore, the answer to the last question is: None (the function never decreases)

Related Questions
What are the domain and range of the function f of x is equal to the quantity x squared plus 6x plus 8 end quantity divided by the quantity x plus 4 end quantity?
A. D: {x ∊ ℝ | x ≠ 4}; R: {y ∊ ℝ | y ≠ 0}
B. D: {x ∊ ℝ | x ≠ −4}; R: {y ∊ ℝ | y ≠ −2}
C. D: {x ∊ ℝ | x ≠ 4}; R: {y ∊ ℝ | y ≠ 2}
D. D: {x ∊ ℝ | x ≠ −2}; R: {y ∊ ℝ | y ≠ 0}
Answers
The domain and range of \(f(x) = \frac{x^{2}+ 6x+8}{x+4}\) is D: {x ∊ ℝ | x ≠ −4}; R: {y ∊ ℝ | y ≠ −2} .
The domain of a function f(x) is set of the value of x for which it is defied and Range of function is set of values f takes .
The rational number \(f(x) = \frac{p(x)}{q(x)}\) where p(x) and q(x) are polynomial in terms of x and q(x) ≠ 0 . The domain of rational number is set of values that do not cause denominator equal to zero .
The given function is :
\(f(x) = \frac{x^{2}+ 6x+8}{x+4}\)
we need to find domain and range of function,
For domain put denominator equals to zero
x+4 = 0
x = -4
so, domain is every real number except number making it zero
domain = (-∞,-4)∪(-4,∞) and x ≠ -4
For range ,factoring numerator
x²+6x+8 = x²+2x+4x+8
x(x+2)+4(x+2) = (x+4)(x+2)
Putting numerator back,
\(f(x) = \frac{(x+4)(x+2)}{x+4}\)
Cancelling factor (x+4) from numerator and denominator
\(f(x) = x+2\)
Putting x+2 = 0
\(x +2 = 0\\x = -2\)
range = (-∞,-2)∪(-2,∞) and f(x) ≠ -2
To know more about Domain and Range here
https://brainly.com/question/28135761
#SPJ1
D: {x ∊ ℝ | x ≠ −4}; R: {y ∊ ℝ | y ≠ −2}
I took the test
Please answer this It would mean alot to me.

Answers
The expression 8x + 4y is not equivalent to 4(2x + 1). Therefore, 8x + 4y = 4(2x + y)
How to find equivalent expression?Two expressions are said to be equivalent if they have the same value irrespective of the value of the variable(s) in them.
Equivalent expressions are expressions that have similar value or worth but do not look the same.
Let's determine whether the expression 8x + 4y is equivalent to 4(2x + 1).
Let's factorise to know whether the expressions are equivalent.
Therefore, using the common factors,
8x + 4y = 4(2x + y)
Hence, the expression are not equivalent .
learn more on equivalent expression here: https://brainly.com/question/28170201
#SPJ1
5 3/10x-1/5(x-y) pls help
Answers
Answer:
3/26/2023, 10:00:19 PM
write a story to illustrate the saying:Monkeys play by their sizes
3/26/2023, 10:00:31 PM
Once upon a time, in a dense forest, there lived different species of monkeys. The monkeys were known for their mischievous nature and their love for playing games. One day, they decided to organize a game of tug-of-war.
The monkeys gathered on either side of a long rope, eager to show off their strength. The bigger and stronger monkeys, like the gorillas and baboons, stood at one end, while the smaller monkeys, like the macaques and tamarins, stood at the other end.
Everyone was excited to start the game, but as soon as it began, it became clear that something was wrong. The larger monkeys easily pulled the smaller ones towards them, causing them to lose the game every time.
The smaller monkeys started complaining, saying that the game was unfair because the bigger monkeys had an advantage over them. But the bigger monkeys simply laughed and said, "Monkeys play by their sizes!"
The smaller monkeys realized that this saying was true. They understood that everyone has their strengths and weaknesses and that they should not try to compete with others who are stronger or more powerful than them. Instead, they decided to play games among themselves, where they could use their own unique skills and abilities to compete fairly.
And so, the monkeys continued to play games and have fun in their own way, without worrying about competing with those who were bigger and stronger. From that day on, they respected each other's differences and played by their own sizes.
3/26/2023, 10:00:59 PM
A rod with a length of 1.6 m is made of aluminum, which has a coefficient of linear expansion of 2.40 ✕ 10−5 (°C)−1. It is initially at a temperature of 25°C.
(a)
What is the change in length of the rod if the temperature drops to 0.0°C? (Give the absolute value in units of mm.)
mm
(b)
How does the rod's length change with lower temperature?
The rod shrinks with lower temperature.
The rod expands with lower temperature.
The rod's length does not change with lower temperature.
(c)
Find the absolute value of the fraction by which the rod's length changes between the two temperatures.
ΔL
L0
=
3/26/2023, 10:01:10 PM
(a) To calculate the change in length of the rod, we can use the formula:
ΔL = αLΔT
where:
α = coefficient of linear expansion
L = initial length of the rod
ΔT = change in temperature
Substituting the given values, we get:
ΔL = (2.40 ✕ 10^-5 (°C)^-1) x (1.6 m) x (25°C - 0.0°C)
ΔL = 0.0096 m
Converting meters to millimeters, we get:
ΔL = 9.6 mm
Therefore, the change in length of the rod is 9.6 mm.
(b) The rod shrinks with lower temperature.
(c) The absolute value of the fraction by which the rod's length changes between the two temperatures can be calculated using the formula:
ΔL
L0
where:
ΔL = change in length of the rod
L0 = initial length of the rod
Substituting the given values, we get:
ΔL
L0
= 0.0096 m / 1.6 m
= 0.006
Therefore, the absolute value of the fraction by which the rod's length changes between the two temperatures is 0.006.
3/26/2023, 10:01:58 PM
prove or disprove if power set a = power set b then a=b discrete math
3/26/2023, 10:02:05 PM
We can disprove the statement "If power set A = power set B, then A = B" using a counterexample.
Let A = {1}, and B = {2}. Then:
Power set of A = {{}, {1}}
Power set of B = {{}, {2}}
Both power sets have two elements: an empty set and a singleton set. Therefore, power set of A is equal to power set of B.
However, A and B themselves are not equal. A contains the element 1 while B contains the element 2. Therefore, we can say that "power set of A = power set of B" does not imply "A = B".
Hence, the statement "If power set A = power set B, then A = B" is false.
3/26/2023, 10:04:17 PM
5 3/10x-1/5(x-y)
3/26/2023, 10:04:27 PM
To simplify the expression 5(3/10)x - 1/5(x - y), we can first distribute the 5 and the -1/5 to get:
(3/2)x - 1/5x + 1/5y
Then, we can combine like terms by adding the coefficients of x and y:
(3/2 - 1/5)x + (1/5)y
To simplify further, we need to find a common denominator for the fractions:
(15/10 - 2/10)x + (2/10)y
Simplifying the numerators, we get:
(13/10)x + (2/10)y
Finally, we can reduce the fractions by dividing both terms by their greatest common factor (GCF) of 1/10:
(130/100)x + (20/100)y
Simplifying further, we get:
(13/10)x + (1/5)y
Therefore, the simplified expression is (13/10)x + (1/5)y.
The graph of an exponential function is given below. Which of the following statements is not true about the function?
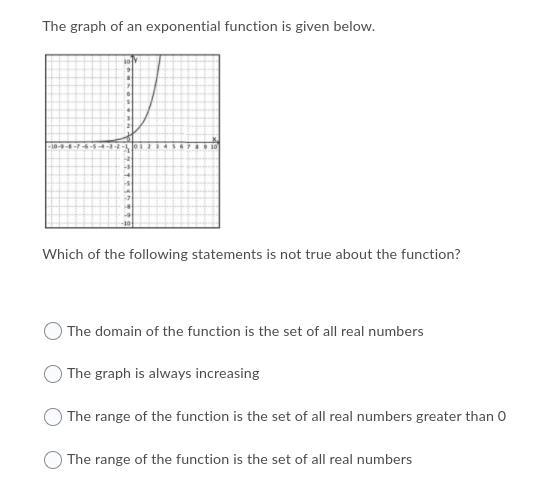
Answers
So we have the graph of an exponential function. This functions have the following general form:
\(f(x)=a\cdot b^{cx},b\ne0\)Since there's an f(x) value for any x value the domain of these functions is the set of all real numbers so the first option is true.
Ano
10 The first term of an AP is 5 and the -3 common difference is Find the 2 term whose value is -20½
Answers
A recent poll found that 35% of those surveyed are worried about aggressive drivers on the road. If three people are selected at random, what is the probability that all three will be worried about aggressive drivers on the road?
Answers
The probability that all three people surveyed is an independent probability and the calculated probability is 0.1225
The probability a surveyed driver is worried = 35%
P(worried) = 0.35 Number of people surveyed = 3Since the probability of being worried is independent ;
Probability = P(A) × P(B) × P(C)The probability that all 3 surveyed are worried :
P(worried) × P(worried) × P(worried) (0.35 × 0.35 × 0.35) = 0.1225Therefore, the probability that all three people surveyed are worried is : 0.1225
Learn more : https://brainly.com/question/18153040
what is 5/8 6 times larger
Answers
Because smaller denominators result in larger fractional pieces, the denominators for the numbers 6 and 8 are 6 and 8, respectively. Therefore, 5/6 will be greater than 5/8.
Which fraction can be determined to be larger?As you saw, you may compare fractions with the same denominator by examining their numerators. As you can see below, 3/4 is larger than 1/4.
The fraction grows as the numerator gets bigger. Due to the fact that it represents a portion of a whole, the fraction 5/8 can never be a whole number. The fraction 5/8 represents 5 of the 8 parts that make up the whole.
Although the decimal 0.625 is equivalent to 5/8, it still does not make a whole. You may represent 5/8 as that. The complete response is provided below. Because smaller denominators result in larger fractional pieces, the denominators for the numbers 6 and 8 are 6 and 8, respectively. Therefore, 5/6 will be greater than 5/8.
To learn more about fraction visit:
brainly.com/question/1067335
#SPJ1
In Exercises 9 to 14, find the limit of each function at the given point, or explain why it does not exist. 10. f(z) = Arg z at Zo--1 11. f(z) = (1-Im z)-1 at z,-8 and then at zo-8 +1 12.f(z) = (z _ 2) log(z-21 at zo = 2 13, f(z) =-, z#0 at zo = 0 14. f(z) = 2+21,
Previous question
Answers
The limit of each function at the given point i n the question 10 to 14, is explained below.
Limit Of A function:A function may get close to two distinct limits. There are two scenarios: one in which the variable approaches its limit by values larger than the limit, and the other by values smaller than the limit. Although the right- and left-hand limits are present in this scenario, the limit is not defined.
When a variable approaches its limit from the right, the function's right-hand limit is the value that approaches.a
10). The limit of f(z) = Arg z as z approaches Zo = 1 does not exist. This is because the argument function is not continuous at the point z = 1, where there is a branch cut.
11). The limit of f(z) = \((1 - lm z)^{-1}\) as z approaches z0 = -8 does not exist. This is because the function approaches infinity as z approaches -8 from the left, and negative infinity as z approaches -8 from the right.
However, if we consider the limit of f(z) as z approaches z0 = -8 + i from both the left and the right, the limit exists and is equal to 0. This is because in the complex plane, the value of Im z cannot exceed 1, so as z approaches -8 + i, the denominator (1 - Im z) approaches 0, and the function approaches infinity. However, the numerator approaches a finite value of 1, which cancels out the denominator, and the overall limit is equal to 0.
12). The limit of f(z) = (z - 2) log(z - 2) as z approaches z0 = 2 is 0. This is because the term (z - 2) approaches 0 as z approaches 2, and log(z - 2) approaches 0 as well because log(z - 2) is continuous at z = 2. Therefore, the limit is equal to 0.
13). The limit of f(z) = -1/z as z approaches z0 = 0 does not exist. This is because as z approaches 0, the magnitude of 1/z approaches infinity, but the direction of approach depends on which quadrant the limit is approached from. Since the limit does not approach a unique value from all directions, the limit does not exist.
14). The limit of f(z) = 2 + \(2^{1/z}\) as z approaches infinity does not exist. This is because as z approaches infinity, the term \(2^{1/z}\) approaches 1, and the limit approaches 2 + 1 = 3. However, if we approach infinity along the real axis, the limit of \(2^{1/z}\) approaches 1, but if we approach infinity along the imaginary axis, the limit of \(2^{1/z}\) approaches infinity. Therefore, the limit of f(z) does not exist.
Learn more about limit of function, visit:
https://brainly.com/question/7446469
#SPJ1
Find the distance between the two points in simplest radical form. ( 3 , − 7 ) and ( − 2 , − 2 ) (3,−7) and (−2,−2)
Answers
Answer: We can use the distance formula to find the distance between the two points (3, -7) and (-2, -2):
distance = √[(x₂ - x₁)² + (y₂ - y₁)²]
where (x₁, y₁) = (3, -7) and (x₂, y₂) = (-2, -2)
distance = √[(-2 - 3)² + (-2 - (-7))²]
distance = √[(-5)² + (5)²]
distance = √[25 + 25]
distance = √50
Simplifying the radical, we can factor out a perfect square of 25 from 50:
distance = √(25 x 2)
distance = 5√2
Therefore, the distance between the two points in simplest radical form is 5√2 units.
Step-by-step explanation:
Lenny buys a popcorn and soda at the movies. A large popcorn is $7 and the drink is $3.50. Lenny has to also pay tax of 6%. How much will he pay in total?
Answers
Answer:
i think its 10.71 i dont know if i got it right your welcome
Step-by-step explanation:
Answer:
$10.71
Step-by-step explanation:
What is the ratio of 4 to 12
Answers
Answer:
3?
Step-by-step explanation:
By using graphical method, find optimal solution of the problem max z = 3x + y s.t 2x - y ≤ 5 -x + 3y ≤ 6 x ≥ 0, y ≥ 0
Answers
By analyzing the graph and evaluating the objective function at each vertex of the feasible region, we can find the optimal solution, which is the vertex that maximizes the objective function z = 3x + y.
To find the optimal solution of the given problem using the graphical method, we need to plot the feasible region determined by the given constraints and then identify the point within that region that maximizes the objective function.
Let's start by graphing the constraints:
1. Plot the line 2x - y = 5. To do this, find two points on the line by setting x = 0 and solving for y, and setting y = 0 and solving for x. Connect the two points to draw the line.
2. Plot the line -x + 3y = 6 using a similar process.
3. The x-axis and y-axis represent the constraints x ≥ 0 and y ≥ 0, respectively.
Next, identify the feasible region, which is the region where all the constraints are satisfied. This region will be the intersection of the shaded regions determined by each constraint.
Finally, we need to identify the point within the feasible region that maximizes the objective function z = 3x + y. The optimal solution will be the vertex of the feasible region that gives the highest value for the objective function. This can be determined by evaluating the objective function at each vertex and comparing the values.
Note: Without a specific graph or additional information, it is not possible to provide the precise coordinates of the optimal solution in this case.
For more such questions on graph
https://brainly.com/question/19040584
#SPJ8
The data manager for a state political party gathered data to determine how many citizens would support the party’s senate candidate. He polled citizens in 30 similarly sized senate districts and found a sample mean of 70,438 citizens. Statewide data shows that the population standard deviation is 645.3. What is the approximate 90% confidence interval for this situation?
Answers
The approximate 90% confidence interval for this situation is given as follows:
(70244, 70632).
What is a z-distribution confidence interval?The bounds of the confidence interval are given by the rule presented as follows:
\(\overline{x} \pm z\frac{\sigma}{\sqrt{n}}\)
In which:
\(\overline{x}\) is the sample mean.z is the critical value.n is the sample size.\(\sigma\) is the standard deviation for the population.From the z-table, the critical value for a 95% confidence interval is given as follows:
z = 1.645.
The parameters are given as follows:
\(\overline{x} = 70438, \sigma = 645.3, n = 30\)
The lower bound of the interval is given as follows:
\(70438 - 1.645 \times \frac{645.3}{\sqrt{30}} = 70244\)
The upper bound of the interval is given as follows:
\(70438 + 1.645 \times \frac{645.3}{\sqrt{30}} = 70632\)
More can be learned about the z-distribution at https://brainly.com/question/25890103
#SPJ1
Greg has 4 shirts: a white one, a black one, a red one, and a blue one. He also has two pairs of pants, one blue and one tan. What is the probability, if Greg gets dressed in the dark, that he winds up wearing the white shirt and tan pants? Show your work. (10 points)
MARKING BRINLIEST AND GIVING A LOT OF POINTS PLSSSS HELP
Answers
The probability, if Greg gets dressed in the dark, that he winds up wearing the white shirt and tan pants is 0.125 or 12.5%.
To find the probability that Greg winds up wearing the white shirt and tan pants while getting dressed in the dark, we need to find out all the possible outfit options. According to the question given, first we nned to find out number of outfit combinations possible.
Total number of Outfit Combinations:
There are 4 shirts: a white one, a black one, a red one, and a blue one and also two pairs of pants, one blue and one tan. So, total number of possible outfit combinations would be 4 * 2 = 8.
No of favourable options:
As given in the question, Greg wears white shirt and tan pants. There is only one white shirt and one tan pant. So, number of favourable options would be only 1 .
Probability = Number of favourable outcomes/Total no. of combinations
Probability = 1/8
Probability = 0.125 or 12.5%
Therefore, the probability, if Greg gets dressed in the dark, that he winds up wearing the white shirt and tan pants is 0.125 or 12.5%.
To study more about Probability:
https://brainly.com/question/13604758
https://brainly.com/question/251701
Express cos M as a fraction in simplest terms.

Answers
\(\begin{array}{llll} \textit{using the pythagorean theorem} \\\\ a^2+o^2=c^2\implies a=\sqrt{c^2 - o^2} \end{array} \qquad \begin{cases} c=\stackrel{hypotenuse}{30}\\ a=\stackrel{adjacent}{MN}\\ o=\stackrel{opposite}{18} \end{cases} \\\\\\ MN=\sqrt{ 30^2 - 18^2} \implies MN=\sqrt{ 576 }\implies MN=24 \\\\[-0.35em] ~\dotfill\\\\ \cos(M )=\cfrac{\stackrel{adjacent}{24}}{\underset{hypotenuse}{30}} \implies \cos(M)=\cfrac{4}{5}\)
A machine has two components both of which have a lifespan, in months, that is exponentially distributed with mean 8. The lifespan of the two components are independent. Find the probability both components are functioning in 12 months.
Answers
Answer:
0.0498
Step-by-step explanation:
In this question,
x~exponential
we have
mean = 1/λ = 8
from here we cross multiply, when we do
such that
λ = 1/8
probability of x functioning in 8 months
= e^-λx
= e^-1/8x12
= e^-1.5
= 0.2231
i got this value through the use of a scientific calculator
then the probability that these two are greater than 12
= 0.2231²
= 0.04977
= approximately 0.0498
therefore the probability that both components are functioning in 12 months is 0.0498

3. Mrs. Smith's class took a survey and found that 9 of 13 students prefer two scoops of ice cream versus one scoop of ice cream. Based on this rate, if 104 students buy ice cream, how many will choose two scoops of ice cream?
Answers
9•104=13x
936=13x
X=72
. In a fort, there were provisions for 400 men for 23 weeks. 60 more men joined them. How long will the provisions
last?
Answers
The additional 60 men, the provisions will last for approximately 20 weeks.
To determine how long the provisions will last with the additional 60 men, we need to consider the total number of people and the original duration the provisions were meant to last.
Originally, the provisions were intended to sustain 400 men for 23 weeks. This means that the provisions were estimated to be sufficient for a total of 400 * 23 = 9200 person-weeks.
Now, with the additional 60 men, the total number of men becomes 400 + 60 = 460.
To calculate how long the provisions will last with the increased number of men, we divide the total person-weeks by the new number of men:
Provisions last = Total person-weeks / Number of men
= 9200 / 460
≈ 20 weeks (rounded to the nearest whole number)
The additional 60 men will extend the supply's shelf life to around 20 weeks.
for such more question on provisions
https://brainly.com/question/1216161
#SPJ8
2/9 h = 8
h=
Pls tell me what h = !
Answers
Answer:
h=36
.......................
Peanut allergies are becoming increasingly common in Western countries. Some evidence points to the timing of peanuts! first introduction in the diet as an influential factor, raising the question of whether pediatricians should recommend early exposure or avoidance. A study enrolled infants with a diagnosed peanut allergy and randomly assigned them to either completely avoid peanuts or consume peanuts in small amounts regularly until they reached 60 months of age. At the end of the study, 18 of the 51 infants who had avoided peanuts were still allergic to peanuts. In contrast, 5 of the 47 infants who had consumed peanuts were still allergic to peanuts. Do the data indicate that one approach is more beneficial? Follow the four‑step process.
STATE: What is the question we are asking?
A. Does early exposure to peanuts better reduce peanut allergy in children with a known allergy to peanuts?
B. Does early exposure to peanuts in small amounts or complete avoidance of peanuts better reduce peanut allergy in children with a known allergy to peanuts?
C. Should all children under the age of 60 months avoid peanuts or only eat them in small amounts?
D. Should all children under 60 months eat peanuts regularly in small amounts?
Answers
Answer:
B. Does early exposure to peanuts in small amounts or complete avoidance of peanuts better reduce peanut allergy in children with a known allergy to peanuts?
Step-by-step explanation:
Remember we are told there's already a question whether pediatricians should recommend early exposure or avoidance. Thus, the research question should answer these two issues (early exposure or avoidance).
Hence, the question we are asking is: Does early exposure to peanuts in small amounts or complete avoidance of peanuts better reduce peanut allergy in children with a known allergy to peanuts?
Rewrite the number in Standard form
1.2 x 107
Answers
Hope that helped XD
Solve this equation.

Answers
Answer:
\(\dfrac{4a^6b^5}{c^3}\)
Step-by-step explanation:
Given expression:
\(\dfrac{8a^4b^{-3}c^{12}}{2a^{-2}b^{-8}c^{15}}\)
Separate like terms:
\(\dfrac{8}{2} \cdot \dfrac{a^4}{a^{-2}}\cdot \dfrac{b^{-3}}{b^{-8}} \cdot \dfrac{c^{12}}{c^{15}}\)
Divide the numbers:
\(4\cdot \dfrac{a^4}{a^{-2}}\cdot \dfrac{b^{-3}}{b^{-8}} \cdot \dfrac{c^{12}}{c^{15}}\)
\(\textsf{Apply the exponent rule} \quad \dfrac{a^b}{a^c}=a^{b-c}:\)
\(4 \cdot a^{4-(-2)} \cdot b^{-3-(-8)} \cdot c^{12-15}\)
Simplify the exponents:
\(4 \cdot a^6 \cdot b^5 \cdot c^{-3}\)
\(\textsf{Apply the exponent rule} \quad a^{-n}=\dfrac{1}{a^n}:\)
\(4 \cdot a^6 \cdot b^5 \cdot \dfrac{1}{c^3}\)
Simplify:
\(\dfrac{4a^6b^5}{c^3}\)
f(g(x)) g(f(x)) ANSWER QUESTION BELOW BRIEF RESPONSE

Answers
Given statement solution is :- "F(g(x)) g(f(x))": The function F(x) is composed with g(x), and the result is further composed with g(f(x)).
"f(g(x)) g(f(x))": The function g(x) is composed with f(x), and the result is further composed with g(f(x)).
The expressions "F(g(x)) g(f(x))" and "f(g(x)) g(f(x))" are compositions of functions. The answer to the question posed would depend on the specific functions F(x) and g(x), as well as f(x) and g(x) in the second expression.
To provide a brief response:
For the expression "F(g(x)) g(f(x))": The function F(x) is composed with g(x), and the result is further composed with g(f(x)). The order of composition is F(g(x)) first, followed by g(f(x)).
For the expression "f(g(x)) g(f(x))": The function g(x) is composed with f(x), and the result is further composed with g(f(x)). The order of composition is f(g(x)) first, followed by g(f(x)).
For such more questions on Compose Function Expressions.
https://brainly.com/question/13033002
#SPJ8
SHEET CAKES
--------------------------------------------
$36 Small (Feeds 12 people)
$46 Medium (Feeds 22 people)
$56 Large (Feeds 32 people)
--------------------------------------------
The new pastry chef at Jackson's Bakery specializes in Sheet cakes for parties. She sold 17 small, 11 medium, and 20 large sheet cakes in one week. How much money did Jackson's Bakery make in one week from sheet cakes?
Answer: $2,245 (I know it for this one but not the next one)
How many people would all of the sheet cakes sold in problem 3 feed?
--------------------------------------------------------------------------------------------------------
(Dont need to tell me the answer just tell the steps I need to do)
Answers
Answer:
The chef sold 17 small sheet cakes. One small sheet cake can feed 12 people, so the small sheet cakes she sold can feed 17*12 people, which is 204 people. Do this for the medium and large sheet cakes as well, and add them up, and you'll get the answer.
Step-by-step explanation:
Hope this helps!
Answer:
1086
Step-by-step explanation:
1. 7x12= 204(small cakes)
2. 11x22=242(medium cakes)
3.20x32=640(large cakes)
4. add all of the products up
so: 204+242+640
= 1086
This should be correct.
A cereal box says that it now contains 25% more cereal. If it originally had 12 ounces of cereal, how much does it have now?
Answers
Answer:
15
Step-by-step explanation:
Answer:
21 ounces.Step-by-step explanation:
This is percentage increase.In order to find that, we simply do:
(100+25)% = 125%
100% = 12 ounces
125% = ?
12*125/100 = 9 ounces
Add it up to the original amount:
12+9 = 21 ounces
My name is nessalovetrillo i am studying to be able to test out of my algebra class so this is a study guide please see picture of the help

Answers
Equation of the Parabola.
If the vertex of a parabola is located at the point (h, k), then the equation of the parabola is written as:
\(y=a(x-h)^2+k\)Where a is the leading coefficient. To find the coordinates of the vertex, given its equation, we use the 'square completion' technique.
We are given the equation:
\(y=x^2-4x-21\)We need to transform this equation so it can be expressed like the general equation given above. Adding and subtracting 4:
\(y=x^2-4x+4-21-4\)Rearranging:
\(y=(x^2-4x+4)-25\)Factoring:
\(y=(x-2)^2-25\)The vertex of the parabola is located at (2, -25).
To find the x-intercepts, we set y=0 and solve the equation:
\(\begin{gathered} (x-2)^2-25=0 \\ \text{Add 25:} \\ (x-2)^2=25 \end{gathered}\)Taking the square root (it has two signs):
\(x-2=\pm5\)Solving for x, we get two possible answers:
x = 5 + 2 = 7
x = -5 + 2 = -3
X-inercepts: -3, 7
In a class of students, the following data
table summarizes how many students have a
cat or a dog. What is the probability that a
student chosen randomly from the class has
a cat?
Has a dog
Does not have a
dog
Has a cat
2
3
Does not have a
cat
12
10
Answers
The table can be summarized as follows:
| | Has a dog | Does not have a dog |
|----------|-----------|---------------------|
| Has a cat | 2 | 3 |
| Does not have a cat | 12 | 10 |
To find the probability that a student chosen randomly from the class has a cat, we need to find the total number of students who have a cat (regardless of whether or not they have a dog), and divide it by the total number of students in the class.
The number of students who have a cat is 2 (those who have a dog and a cat) + 3 (those who have a cat but do not have a dog) = 5.
The total number of students in the class is the sum of all four categories: 2 (has a cat and a dog) + 3 (has a cat, does not have a dog) + 12 (does not have a cat, has a dog) + 10 (does not have a cat, does not have a dog) = 27.
So, the probability that a student chosen randomly from the class has a cat is 5/27.
Cách tính chu vi hình vuông?
Answers
Answer:
Xin hãy đánh dấu cho tôi là một người tồi tệ nhất
Để tìm chu vi hình vuông, bạn phải nhân 2 cạnh với 4..
Sử dụng công thức
chu vi = 4 * (một mặt)
Which choice below DOES NOT name of one of the four quadrants of the coordinate plane?
Quadrant Ⅲ
Quadrant Ⅱ
Quadrant Ⅴ
Quadrant Ⅰ
Answers
Answer:
Quadrant V
Step-by-step explanation:
A co-ordinate graph only has 4 quadrants!
find the lcm 15 and 20
Answers
Answer:
5
Step-by-step explanation:
Solution:
15 20
/ \ / \
3 5 2 10
/ \
2 5
3*5*2*2=60