a washing machine can hold 3/4 kg of laundry in each load. if randy has . 6 kilograms of laundry, how many loads does he need to do? 5 6 7 d8
Answers
Randy needs 8 loads.
To find the answer on the question we have to follow the method of multiplication and division .
A washing machine can hold \(\frac{3}{4}\) kg of laundry in each load.
\(\frac{3}{4}\) kg of laundry is equal to 1 load.
\(\frac{3}{4}\) kg of laundry = 1 load
1 kg of laundry = \(\frac{1 * 4}{3}\) load ( following the method of division )
1 kg of laundry = \(\frac{4}{3}\) load
Randy has 6kg of laundry.
So, 1kg of laundry i.e \(\frac{4}{3}\) load is to be multiplied by 6.
6kg of laundry = \(\frac{4 * 6}{3}\) load ( following the method of multiplication)
= 8 loads
Hence, Randy needs 8 loads.
Read more about multiplication :
https://brainly.com/question/26669440
#SPJ4
Related Questions
Jill wants to save to buy a car. She decides to open a banking account that is offering a simple interest rate of 4.5% annually. How much will Jill have in her account after 5 years if she deposits $7,000 today?
Answers
Answer:The interest is: $1575
The total is: $8575
Step-by-step explanation:
7000*5*0.045 gets you the interest
Then you add the original amount, 7000, to the total
1575 + 7000 = $8575
In July 2008, a forest fire near the Park Yosemite National burned about 53 miles squares of forest. If a square mile equals 640 acres, about how many acres of forest were burned?
Answers
Answer:
33,920 acres of forest were burned.
Step-by-step explanation:
In this case, since you know that a square mile is equal to 640 acres, you can use a rule of three to find the acres that are equivalent to 53 square miles:
1 square mile → 640 acres
53 square miles → x
x=(53*640)/1
x=33,920 acres
According to this, the answer is that 33,920 acres of forest were burned.
Given that AB = 370 m and AC = 510 m, find
(i) the distance between B and C,
(ii) ACB,
(iii) the bearing of C from B,
(iv) the shortest distance from A to BC.

Answers
Answer:
(i) The distance between B and C is approximately 552.9 m
(ii) ∠ACB is approximately 40.49°
(iii) The bearing of C from B is approximately 184.49°
(iv) The shortest distance from A to BC is approximately 331.155 m
Step-by-step explanation:
The given parameters are;
The length of segment AB = 370 m
The length of segment AC = 510 m
The bearing of B from A = 68°
The bearing of C from A = 144°
(i) From the bearing of B from A = 68° and the bearing of C from A = 144°, we have;
∠BAC = 144° - 68° = 76°
∠BAC = 76°
Let A represent ∠BAC, c represent segment AB, b represent segment AC, and a represent segment BC, by cosine rule, we have;
a² = b² + c² - 2·b·c·cos(A)
By substituting the known values, we get;
a² = 510² + 370² - 2 × 510 × 370 × cos(76°)
a² ≈ 397000 - 91301.3234 ≈ 305698.677
BC = a ≈ √(305,698.677) ≈ 552.9
The distance between B and C, BC ≈ 552.9 m
(ii) By sine rule, we have;
a/(sin(A) = b/(sin(B)) - c/(sin(C))
Therefore;
552.9/(sin (76°)) = 370/(sin(C))
sin(C) = 370/(552.9/(sin (76°))) ≈ 0.649321
C = arcsine(0.649321) ≈ 40.49°
∠C = ∠ACB ≈ 40.49°
(iii) Angle ∠B = ∠ABC = 180° - 76° - 40.49° ≈ 63.51°
The bearing of A from B = 360° - (180° - 68°) = 248°
Therefore, the bearing of C from B ≈ 248° - 63.51° ≈ 184.49°
(iv) The shortest distance from A to BC = 370 m × sin(63.51°) ≈ 331.155 m
An element with a mass of 680 grams decays by 27.7% per minute. To the nearest minute, how long will it be until there are 2 grams of the element remaining?
Answers
Answer:
18
Step-by-step explanation:
I just know
In a first aid kit, the ratio of large bandages to small bandages is 1 to 6. Based on this ratio, how many small bandages are in a kit of 140 bandages?
Answers
Compute the first‑order partial derivatives of the function. w= 13x/ (x^2+ y^2 +z^2)^3/2
dw/dx= _________
Answers
the first-order partial derivative of w with respect to x is:
dw/dx = [13 * (x^2 + y^2 + z^2)^(3/2) - 39x^2] / (x^2 + y^2 + z^2)^3
Determine the partial derivative?To compute the partial derivative dw/dx, we differentiate the function with respect to x while treating y and z as constants.
To compute the first-order partial derivative of the function w = 13x / (x^2 + y^2 + z^2)^(3/2) with respect to x, we differentiate the function with respect to x while treating y and z as constants.
Using the quotient rule and the chain rule, the derivative is calculated as follows:
dw/dx = [13 * (x^2 + y^2 + z^2)^(3/2) - 13x * (3/2) * (2x)] / (x^2 + y^2 + z^2)^3
Simplifying the derivative:
dw/dx = [13 * (x^2 + y^2 + z^2)^(3/2) - 39x^2] / (x^2 + y^2 + z^2)^3
Therefore, the first-order partial derivative of w with respect to x is:
dw/dx = [13 * (x^2 + y^2 + z^2)^(3/2) - 39x^2] / (x^2 + y^2 + z^2)^3
To know more about partial derivative, refer here:
https://brainly.com/question/6732578#
#SPJ4
Solve the following system of equations
by Substitution.
5x + 4y = 7
-2x - 2y = 8

Answers
Answer:
y = 9/13
Step-by-step explanation:
x = -4 + y
5(-4 + y) + 4y = 7
-20 + 9y = 7
9y = -13
Answer:
5x + 4y = 7 × -2
-2x - 2y = 8 × 5
-10x - 8y = -14
-10x - 10y = 40
Step-by-step explanation:
2y = -54 ÷2
y = -27
Now substitute the value of y into equation (1)
5x + 4y = 7
5x + 4(-27) = 7
5x = 7 + 108
5x = 115
X = 23
A tank has a hole in it which leaks water at a rate of 335 ml per minute .If the tank is empty after 4 hours and 25 minutes ,how many litres of water can the tank hold?Give ur answer correct to 1 decimal place
Answers
Change the length of time to minutes:
1 hour = 60 minutes.
4 hours x 60 = 240 minutes + 25 minutes = 265 minutes
Multiply leak rate by total minutes:
265 x 335 = 88,775 ml
Half the tank was 88,775 ml
Multiply by 2 to get the full tank amount:
88775 x 2 = 177,550 ml
Divide by 1000 to change to liters:
177,550 / 1000 = 177.55 liters
Answer to 1 decimal place = 177.6 Liters
The Atlantic Ocean region contains approximately 2 × 10^16 gallons of water. Lake Ontario has approximately 8,000,000,000,000 gallons of water. How many Lake Ontarios would it take to fill the Atlantic Ocean region in terms of gallons of water?
Answers
Answer:
2500 gallons or water.
Step-by-step explanation:
Atlantic ocean contains 2 x 10¹⁶ gallons of water.
lake Ontario has approx 8 x 10¹² gallons of water.
req'd:
how many lake ontarios would it take to fill the Atlantic ocean in gallons of water?
= 2 x 10¹⁶ gallons of water
8 x 10¹² gallons of water
= 2500 Lake Ontarios to fill The Atlantic Ocean
2500 times the gallons of water Lake Ontarios will take to fill the Atlantic Ocean region.
Given that,
The Atlantic Ocean region contains approximately 2 × 10^16 gallons of water.
Lake Ontario has approximately 8,000,000,000,000 gallons of water or 8 * 10¹².
To determine how many Lake Ontarios would it take to fill the Atlantic Ocean region in terms of gallons of water
The ratio can be defined as the proportion of the fraction of one quantity towards others. e.g.- water in milk.
Here,
Lake Ontarios would it take to fill the Atlantic Ocean region
= 2 × 10¹⁶ / 8 * 10¹²
= 0.25 * 10⁴
= 2500 times the gallons of water Lake Ontarios
Thus, 2500 times the gallons of water Lake Ontarios will take to fill the Atlantic Ocean region.
Learn more about ratios here:
brainly.com/question/13419413
#SPJ2
Ramil and Carly decided to make more baked goods for the bake sale. They used 1/8 less flour to make bread
Answers
Using fraction formula ,
The flour used by ramil and Carly for making bread is 33/40lb
Fraction: fraction is a number represented as a quotient, in which a numerator is divided by a denominator.
We have given that,
Ramil and Carly used 1/2 lb flour to make the bread.
They used 1/8lb less flour to make bread than to make cookies.
So, they used flour to make the cookies = 1/2+1/8
= 5/8lb
Therefore they used 5/8lb flour to make the cookies.
they used 1/5 lb more breads to make cookies than to make brownies. Mathematically, they used cookies for making the brownies is
= 1/5 + 5/8
=(8 + 25)/40 = 33/40lb
Therefore , they used 33/40lb flour to make the brownies.
To learn more about Fraction,
https://brainly.com/question/6591603
#SPJ4
Complete question:
Ramil amd carly decided to make more baked goods for the bake sale. They used 1/8 lb less flour to make bread than to make cookies. She used 1/5 lb more to make cookies than to make brownies. If she used 1/2 lb of flour to make the bread, how much flour did she use to make the brownies
Write an equation in slope-intercept form for the line that is parallel to the line 6x + 2y = 2 and passes through the point
(-1, 7).
Answers
Answer:
\(y=-3x+4\)
Step-by-step explanation:
Hi there!
What we need to know:
Slope-intercept form: \(y=mx+b\) where m is the slope and b is the y-intercept (the value of y when the line crosses the y-axis)Parallel lines have the same slope (m) and different y-intercepts (b)1) Determine the slope (m)
\(6x+2y=2\)
Rearrange this equation in slope-intercept form (so it's easier for us to identify the slope)
Subtract 6x from both sides to isolate 2y
\(6x+2y-6x=-6x+2\\2y=-6x+2\)
Divide both sides by 2 to isolate y
\(y=-3x+1\)
Now, we can tell clearly that -3 is in the place of m. Therefore, because parallel lines have the same slope, we know that the line we're solving for will also have a slope of -3. Plug this into \(y=mx+b\):
\(y=-3x+b\)
2) Determine the y-intercept
\(y=-3x+b\)
Plug in the given point (-1,7)
\(7=-3(-1)+b\\7=3+b\)
Subtract 3 from both sides
\(7-3=3+b-3\\4=b\)
Therefore, the y-intercept of the line is 4. Plug this back into \(y=-3x+b\):
\(y=-3x+4\)
I hope this helps!
let x,y be independent bernoulli(1/2) random variables. let z be a random variable that takes the value 1 if x y =1, and 0 otherwise. show that x,y,z are pairwise, but not mutually, independent.
Answers
x, y, and z are pairwise independent because any two of them are independent. x, y, and z are not mutually independent because their joint distribution does not factor into the product of their marginal distributions.
To show that the random variables x, y, and z are pairwise independent but not mutually independent, we need to examine the definitions of these concepts and demonstrate the properties.
Pairwise Independence:
Two random variables are said to be pairwise independent if any two of them are independent, regardless of the dependence on the third variable.
Mutual Independence:
Three random variables are said to be mutually independent if each pair of them is independent and their joint distribution factors into the product of their marginal distributions.
Now let's analyze x, y, and z based on these definitions.
Pairwise Independence:
To show that x, y, and z are pairwise independent, we need to demonstrate that any two of them are independent, regardless of the dependence on the third variable.
a) x and y:
Since x and y are independent Bernoulli(1/2) random variables, their outcomes do not affect each other. Therefore, x and y are independent.
b) x and z:
We need to consider the joint distribution of x and z. Let's examine all possible combinations:
If x = 0, then regardless of the value of y, z will be 0. Hence, P(x = 0, z = 0) = P(x = 0)P(z = 0) = (1/2)(1) = 1/2.
If x = 1, then z will be 1 only when y = 1. Therefore, P(x = 1, z = 1) = P(x = 1, y = 1) = P(x = 1)P(y = 1) = (1/2)(1/2) = 1/4.
If x = 1, then z will be 0 when y = 0. Therefore, P(x = 1, z = 0) = P(x = 1, y = 0) = P(x = 1)P(y = 0) = (1/2)(1/2) = 1/4.
If x = 0, then regardless of the value of y, z will be 0. Hence, P(x = 0, z = 0) = P(x = 0)P(z = 0) = (1/2)(1) = 1/2.
From the above calculations, we can see that P(x, z) = P(x)P(z) for all possible combinations of x and z. Therefore, x and z are independent.
c) y and z:
Similar to the analysis above, we can calculate the joint probabilities:
If y = 0, then regardless of the value of x, z will be 0. Hence, P(y = 0, z = 0) = P(y = 0)P(z = 0) = (1/2)(1) = 1/2.
If y = 1, then z will be 1 only when x = 1. Therefore, P(y = 1, z = 1) = P(y = 1, x = 1) = P(y = 1)P(x = 1) = (1/2)(1/2) = 1/4.
If y = 1, then z will be 0 when x = 0. Therefore, P(y = 1, z = 0) = P(y = 1, x = 0) = P(y = 1)P(x = 0) = (1/2)(1/2) = 1/4.
If y = 0, then regardless of the value of x, z will be 0. Hence, P(y = 0, z = 0) = P(y = 0)P(z = 0) = (1/2)(1) = 1/2.
From the above calculations, we can see that P(y, z) = P(y)P(z) for all possible combinations of y and z. Therefore, y and z are independent.
We have shown that any two random variables among x, y, and z are independent. Hence, x, y, and z are pairwise independent.
Not Mutually Independent:
To demonstrate that x, y, and z are not mutually independent, we need to show that their joint distribution does not factor into the product of their marginal distributions.
To do this, let's consider the joint distribution of x, y, and z. We can analyze all possible combinations:
If x = 0 and y = 0, then z will be 0. Hence, P(x = 0, y = 0, z = 0) = P(x = 0)P(y = 0)P(z = 0) = (1/2)(1/2)(1) = 1/4.
If x = 1 and y = 1, then z will be 1. Hence, P(x = 1, y = 1, z = 1) = P(x = 1)P(y = 1)P(z = 1) = (1/2)(1/2)(1/2) = 1/8.
However, if we examine the joint probability P(x = 0, y = 0, z = 1), we find that it is not equal to P(x = 0)P(y = 0)P(z = 1). In this case, P(x = 0, y = 0, z = 1) is 0 because z can only be 0 when x and y are both 0. Therefore, P(x = 0, y = 0, z = 1) ≠ P(x = 0)P(y = 0)P(z = 1).
Since the joint distribution does not factor into the product of the marginal distributions for all possible combinations, x, y, and z are not mutually independent.
To know more about pairwise independent,
https://brainly.com/question/31037593
#SPJ11
Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the given axis. (a) y=4x−x^2,y=x; rotated about the y-axis. (b) x=−3y^2+12y−9,x=0; rotated about the x−axis. (b) y=4−2x,y=0,x=0; rotated about x=−1
Answers
Therefore, the volume generated by rotating the region bounded by the curves \(y = 4x - x^2\) and y = x about the y-axis is 27π/2.
(a) To find the volume generated by rotating the region bounded by the curves \(y = 4x - x^2\) and y = x about the y-axis, we can use the method of cylindrical shells.
The height of each shell will be given by the difference between the functions \(y = 4x - x^2\) and y = x:
\(h = (4x - x^2) - x \\ = 4x - x^2 - x \\= 3x - x^2\)
The radius of each shell will be the distance between the curve \(y = 4x - x^2\) and the y-axis:
r = x
The differential volume element of each shell is given by dV = 2πrh dx, where dx represents an infinitesimally small width in the x-direction.
To find the limits of integration, we need to determine the x-values where the curves intersect. Setting the two equations equal to each other, we have:
\(4x - x^2 = x\\x^2 - 3x = 0\\x(x - 3) = 0\)
This gives us x = 0 and x = 3 as the x-values where the curves intersect.
Therefore, the volume V is given by:
V = ∫[0, 3] 2π\((3x - x^2)x dx\)
Integrating this expression will give us the volume generated by rotating the region.
To evaluate the integral, let's simplify the expression:
V = 2π ∫[0, 3] \((3x^2 - x^3) dx\)
Now, we can integrate term by term:
V = 2π \([x^3 - (1/4)x^4]\) evaluated from 0 to 3
V = 2π \([(3^3 - (1/4)3^4) - (0^3 - (1/4)0^4)]\)
V = 2π [(27 - 27/4) - (0 - 0)]
V = 2π [(27/4)]
V = 27π/2
To know more about volume,
https://brainly.com/question/32942148
#SPJ11
the areas of two similar triangles are 42cm and 262.5cm. if the altitude of the smaller triangle is 7cm. what is the length of the base of the larger triangle?
Answers
Answer:
75 cm
Step-by-step explanation:
It is given that the triangles are similar. It means that the ratio of their areas are equal to the ratio of their bases and ratio of their altitudes.
Let \(A_1\) be the area of 1st triangle.
Let \(A_2\) be the area of 2nd triangle.
Let \(h_1\) be the altitude of 1st triangle.
Let \(h_2\) be the altitude of 2nd triangle.
Let \(b_1\) be the base of 1st triangle.
Let \(b_2\) be the base of 2nd triangle.
Then \(A_1: A_2 = h_1 : h_2 = b_1 : b_2 ...... (1)\)
\(A_1 = 42 cm^{2} \\A_2 = 262.5 cm^{2}\\h_1 = 7 cm\\b_2 = ?\)
We know that area of a triangle is:
\(A = \dfrac{1}{2} \times b \times h\)
Area of smaller triangle:
\(\frac{1}{2} \times b_1 \times 7 = 42\\\Rightarrow b_1 = 12 cm\)
Now, using part of equation (1):
\(A_1: A_2 = b_1 : b_2 \\\Rightarrow \dfrac{42}{262.5} = \dfrac{12}{b_2}\\\Rightarrow b_2 = 75 cm\)
Hence, base of larger triangle = 75 cm
can i please get the answer to this please? It would be an honor

Answers
Answer: The slope of function A is less than the slope of function B
Step-by-step explanation:
The slope of function B is 4 which comes from y=4x+5.
To find the slope of function A, we pick any two points on the line and then calculate the slope. I have chosen (0,0) and (1,2). Now, we use the formula to solve the slope:
\(m=\frac{y_2-y_1}{x_2-x_1}=\frac{2-0}{1-0}=\frac{2}{1}=2\)
So the slope of function A is 2, which is then the slope of function B which is 4.
Plz help!! Math isn’t my thing. I’ll give brainliest.

Answers
Answer:
Here is your answer
Hope it helps

Answer:
(2,-6)
Step-by-step explanation:
it is above in the photo.

Find an equation for the surface consisting of all points p for which the distance from p to the x-axis is 4 times the distance from p to the yz-plane.
Answers
The equation that represents the distance is -25x² + y² + z² = 0
What is an Equation in Math?An expression, often known as a mathematical expression, is a finite collection of symbols that are well-formed in accordance with context-dependent principles. A mathematical statement called an equation demonstrates the equality of two mathematical expressions.Numbers (constants), variables, operations, functions, brackets, punctuation, and grouping can all be represented by mathematical symbols, which can also be used to indicate the logical syntax's order of operations and other features.In mathematics, an equation is a relationship between two expressions that is expressed as an equality on each side of the equal to sign. An equation would be 3y = 16, for instance.Equations can be divided into the three categories of linear equations, quadratic equations, and cubic equations depending on their degree.Given data :
The distance between two points, is the number of units between them.
The equation that represents the distance is -25x² + y² + z² = 0
The distance between a point and the x-axis is represented as:
D = ( y² + x² ) \(\frac{1}{2}\)
From the question, we have:
D = 5x
Equate both expressions for D
5x =- ( y² + z² ) \(\frac{1}{2}\)
Square both sides
25x² = y² + z²
Equate to 0
y² + z² - 25x² = 0
Rewrite as:
-25x² + y² + z² = 0
Hence, the equation that represents the distance is -25x² + y² + z² = 0
Learn more about Equations refer to :
https://brainly.com/question/29174899
#SPJ4
Jeremiah answers 90% of the questions on his test correctly. There are 40 questions on the test. Jeremiah writes the expression 40 minus (StartFraction 1 over 10 EndFraction times 40) to determine the number of questions answered correctly. Which is an equivalent expression?
Answers
Answer:
A 9/10 x 40
Step-by-step explanation:
Answer:
A
Step-by-step explanation:
please answer, i have 5 mins
Use each of these rules to create 4 ordered pairs using the two sequences.
The first rule is add 12, then divide by 2, starting from 4.
The second rule is multiply by 2, then subtract 2, starting from 3.
Which table shows the 4 ordered pairs created using the two sequences?
A table with three columns. The first column is labeled rule 1, the second column is labeled rule 2, and the third column is labeled ordered pair. There are four rows below the heading row. Under column rule 1 are the numbers zero, four, six, and seven. Under column rule 2 are the numbers three, five, nine, and seventeen. Under the column labeled ordered pair are zero and three, four and five, six and nine, and seven and seventeen.
A table with three columns. The first column is labeled rule 1, the second column is labeled rule 2, and the third column is labeled ordered pair. There are four rows below the heading row. Under column rule 1 are the numbers two, six, eight, and nine. Under column rule 2 are the numbers two, four, ten, and twenty-eight. Under the column labeled ordered pair are two and two, six and four, eight and ten, and nine and twenty-eight.
A table with three columns. The first column is labeled rule 1, the second column is labeled rule 2, and the third column is labeled ordered pair. There are four rows below the heading row. Under column rule 1 are the numbers four, eight, ten, and eleven. Under column rule 2 are the numbers three, four, six, and ten. Under the column labeled ordered pair are four and three, eight and four, ten and six, and eleven and ten.
A table with three columns. The first column is labeled rule 1, the second column is labeled rule 2, and the third column is labeled ordered pair. There are four rows below the heading row. Under column rule 1 are the numbers six, eight, twelve, and twenty. Under column rule 2 are the numbers one, eight, twenty-two, and fifty. Under the column labeled ordered pair are six and one, eight and eight, twelve and twenty-two, and twenty and fifty.
Answers
Ordered pairs must be placed in the following order: (6, 1), (8, 8), (12, 22). (20, 50). The right answer is D.
What is arithmetic?According to the assertions, it deals with a number of operations in mathematics.
For the first series, let the number be x, and for the second, let it be y.
The first rule is to multiply by 2, then, beginning with 6, remove 4.
The sequence can be written as 6 is the first number: = 2x - 4
next number = 2(6) - 4
= 12-4
= 8
The following phrase is thus 8. The following two terms can be written as 12 and 20.
Values of x = 6, 8, 12, 20
The second rule is to add three and then multiply by two, counting backward from one.
= (y + 3)2
First term = 1
Next term = (1 + 3)2
= 8
The next two words can be acquired in a similar manner.
y = 1, 8, 22, 50
Therefore, ordered pairs must be placed in the following order: (6, 1), (8, 8), and (12, 22). (20, 50). The right answer is D.
Know more about arithmetic here:
brainly.com/question/14753192
#SPJ1
Correct question:
The first rule is to multiply by 2, then subtract 4 starting from 6. The second rule is to add 3, then multiply by 2 starting from 1. What are the first four ordered pairs using the two sequences?
A. (0, 0) (6, 1), (8, 2), (12, 22)
B. (6, 1), (10, 8), (14,22), (22, 50)
C. (6, 1), (8, 8), (12, 20), (20, 45)
D. (6, 1), (8, 8), (12, 22), (20, 50)
first two common multiples of 3, 4 and 6
..
Answers
Answer:12 24
Step-by-step explanation:
these are the first in a set of common multiples involving these three numbers
Triangle ABC has perimeter 20 cm.
AB = 7 cm.
BC = 4 cm.
By calculation, deduce whether triangle ABC is a right-angled triangle
Answers
Answer: 28.
Step-by-step explanation: Because if you times 7 and 4 you get 28.
Please help...
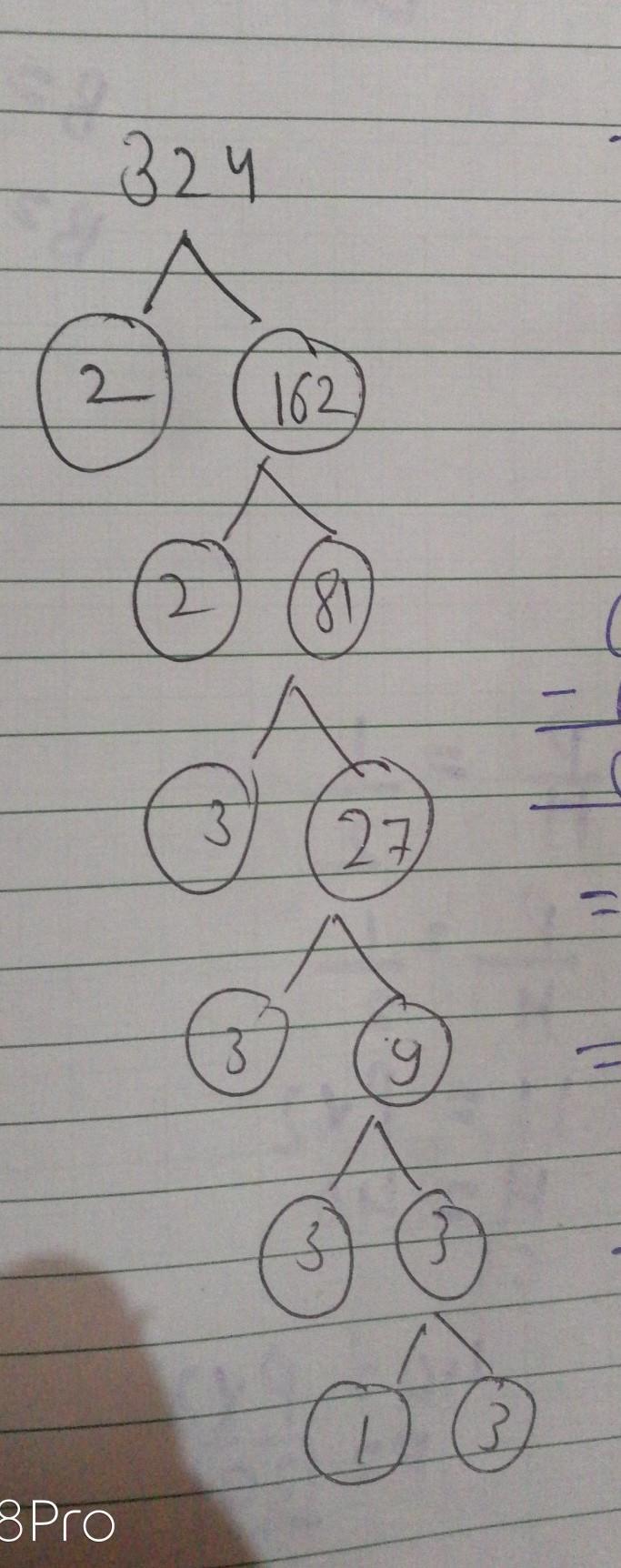
Write 324 as a product of its prime factors
Answers
Answer:
324=
\(2 \times 2 \times 3 \times 3 \times 3 \times 3\)
\( = 2 {}^{2} \times 3 {}^{4} \)
A cleaning company charges $140 for each office it cleans. The fixed monthly cost of $450 for the company includes telephone service and the depreciation on cleaning equipment and a van. The variable cost is $50 per office and includes labor, gasoline, and cleaning supplies. (a) Write a linear cost function representing the cost Cx (in $) to clean x offices per month. (b) Write a linear revenue function representing the revenue Rx (in $) for cleaning x offices per month. (c) Determine the number of offices to be cleaned per month for the company to break even. (d) If 25 offices are cleaned, will the company make money or lose money
Answers
Answer:
a) C(x)=50x+450
b) R(x) = 140x
c) Company will have to clean 5 offices to break even
d) Company will make money, $1,800
Step-by-step explanation:
a) C(x) = 50x+450
b) R(x)=140x
c) to break even, C(x) = R(x)
140x=50x+450
90x=450
x=5
Company will have to clean 5 offices to break even
d) R(x)= 140*25 = 3,500
C (x)=50*25+450 = 1,700
total profit will be 3500-1700 = 1,800
so company will make money
Several friends (Calvin, Dean, Kelli, and Lee) went to Cal's Late Night Diner for a bite to eat. Match each person to their drink (Iced tea, Lemonade, Root Beer, and Water) and determine how much each paid ($4.99, $5.99, $6.99, and $7.99) for their meal.
Clues:
1. The Diner who paid $4.99 was either Calvin or the one who got the Root Beer.
2. Kelli paid $6.99
3. The one who got the water paid 1 dollar less than Dean.
4. Calvin paid more than Lee.
5. The one who got the Root beer paid 1 dollar less than the one who got the Iced Tea.
Answers
Based on the given clues, we can determine the person, drink, and price paid for each individual:
Calvin: Root Beer, $4.99
Dean: Lemonade, $7.99
Kelli: Water, $6.99
Lee: Iced Tea, $5.99
How to determine how much each friends paidFrom clue 1, we know that either Calvin or the person who got the Root Beer paid $4.99. Since Calvin paid more than Lee according to clue 4, Calvin cannot be the one who got the Root Beer. Therefore, Calvin paid $4.99.
From clue 2, Kelli paid $6.99.
From clue 3, the person who got the water paid $1 less than Dean. Since Dean paid the highest price, the person who got the water paid $1 less, which means Lee paid $5.99.
From clue 5, the person who got the Root Beer paid $1 less than the person who got the Iced Tea. Since Calvin got the Root Beer, Lee must have gotten the Iced Tea.
Therefore, the final assignments are:
Calvin: Root Beer, $4.99
Dean: Lemonade, $7.99
Kelli: Water, $6.99
Lee: Iced Tea, $5.99
Learn more about word problems at https://brainly.com/question/21405634
#SPJ1
I only want the answer for A, B, C, no need explanation

Answers
in order
median
mean
mode
Given the following table and graph write the equation to represent the exponential function.

Answers
Answer:
The exponential equation is y = -2×(1/2)^x
Step-by-step explanation:
Ok we have a couple things to note here:
1) The horizontal asymptote of the function is the x axis (always nice)
2) At x=0, y=-2 (i.e, this function will be multiplied by -2 bc the exponent part will transform into one at x=0)
3) Then we need to ascertain the base of the exponential. Based on the facts that at x=1, y=-1 and the "a-value" is -2, we can set up an equation to find b:
y=a×b^x----> -1 = (-2)(b) ------> b=1/2
Therefore, the exponential equation is y = -2×(1/2)^x
Test:
At x = 0, y= -2
At x = -1, y = (-2)*(1/2)^-1 = (-2)*2 = -4
At x=2, y = (-2)*(1/2)^2= (-2)*(1/4) = -1/2
Thus we can be quite certain that this is correct
tell me which ones to put in the boxes

Answers
Answer:
first 0.167 irrational number
second \(\frac{2}{9}\) rational number
\(\pi\) is an irrational number
\(\sqrt{225}\) is a rational number
\(\sqrt[3]{125}\) rational number
Step-by-step explanation:
A rational number is a number that is in the form of p/q, where p and q are integers, and q is not equal to 0
An irrational number is a type of real number which cannot be represented as a simple fraction.

Please help me with this math problem!! :) I will mark brainliest!! :)

Answers
Answer:
x = 36
Step-by-step explanation:
180 - 48 = 132
This is because angle AC- and ACB form a straight angle (180 degrees).
132 + 12 = 144
180 - 144 = 36
The three interior sides of a triangle always add up to 180 degrees.
Hope this helps!
What is the greatest common factor of 36 and 60?
Answers
Answer: 12
Step-by-step explanation: Find the factors of 36 and 60
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Both have 12 in the factors so it is 12 the GCF.
is the point below which a specified percentage of the observations fall.
Answers
In mathematics, the point below which a specified percentage of the observations fall is commonly referred to as the percentile.
A percentile is a measure that indicates the relative position of a particular value within a dataset.
For example, if a value is at the 80th percentile, it means that 80% of the observations in the dataset are below that value, and only 20% of the observations are above it.
Percentiles are often used to analyze and understand the distribution of data, especially in fields such as statistics, probability, and data analysis. They provide insights into how individual data points compare to the overall dataset and help identify outliers or extreme values.
A percentile is a statistical measure that indicates the relative standing of a particular value within a dataset. It represents the point below which a specified percentage of the observations or data points fall. Percentiles are primarily used to understand the distribution of data and analyze how individual values compare to the overall dataset.
To calculate a percentile, the dataset is arranged in ascending order, from the smallest value to the largest value. The position of a specific percentile is then determined based on the percentage of data points below it. For example, the 75th percentile represents the value below which 75% of the data points fall.
Percentiles are commonly used in various fields, including statistics, probability, and data analysis. They provide valuable insights into the spread, variability, and distribution of data. Here are a few key points to consider:
1. Median: The median is the 50th percentile, representing the value that divides the dataset into two equal halves. It is a measure of central tendency and provides information about the middle point of the distribution.
2. Quartiles: Quartiles divide the dataset into four equal parts. The first quartile, or the 25th percentile (Q1), represents the value below which 25% of the data points fall. The third quartile, or the 75th percentile (Q3), represents the value below which 75% of the data points fall. The difference between Q3 and Q1 is known as the interquartile range (IQR) and provides insights into the spread of the middle 50% of the data.
3. Percentile Ranks: Percentile ranks indicate the percentage of data points that are below a specific value. For example, if a student scores in the 80th percentile on a standardized test, it means they performed better than 80% of the test-takers.
4. Outliers: Percentiles can be useful in identifying outliers, which are data points that significantly deviate from the rest of the dataset. Extremely high or low percentiles may indicate unusual or extreme values that warrant further investigation.
5. Normal Distribution: In a normal distribution, the 50th percentile (median) coincides with the mean and mode, and specific percentiles have known standard deviations from the mean (e.g., the 68-95-99.7 rule).
Percentiles are versatile tools for summarizing and analyzing data, providing valuable insights into the distribution and relative positions of individual values. They enable comparisons and help make informed decisions based on the characteristics of a dataset.
to more about Median visit:
brainly.com/question/1153198
#SPJ11