A university considers giving only pass/fail grades to freshmen to reduce competition and stress. The student newspaper interviews faculty members and reports their opinions of the proposed policy. Suppose that 70% of the faculty favor the pass/fail proposal. Assuming 50 faculty members are interviewed. The goal is to find the probability that a majority (26 or more) will favor the proposal.
Answers
Answer:
0.9983 = 99.83% probability that a majority will favor the proposal.
Step-by-step explanation:
We use the normal approximation to the binomial to solve this question.
Binomial probability distribution
Probability of exactly x sucesses on n repeated trials, with p probability.
Can be approximated to a normal distribution, using the expected value and the standard deviation.
The expected value of the binomial distribution is:
\(E(X) = np\)
The standard deviation of the binomial distribution is:
\(\sqrt{V(X)} = \sqrt{np(1-p)}\)
Normal probability distribution
Problems of normally distributed distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
When we are approximating a binomial distribution to a normal one, we have that \(\mu = E(X)\), \(\sigma = \sqrt{V(X)}\).
Suppose that 70% of the faculty favor the pass/fail proposal. Assuming 50 faculty members are interviewed.
This means, respectively, that \(p = 0.7, n = 50\)
Mean and standard deviation:
\(\mu = E(X) = np = 50*0.7 = 35\)
\(\sigma = \sqrt{V(X)} = \sqrt{np(1-p)} = \sqrt{50*0.7*0.3} = 3.24\)
Probability that a majority (26 or more) will favor the proposal.
Using continuity correction, this is \(P(X \geq 26 - 0.5) = P(X \geq 25.5)\), which is 1 subtracted by the pvalue of Z when X = 25.5. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{25.5 - 35}{3.24}\)
\(Z = -2.93\)
\(Z = -2.93\) has a pvalue of 0.0017
1 - 0.0017 = 0.9983
0.9983 = 99.83% probability that a majority will favor the proposal.
Related Questions
Which expression is equivalent to
,10 ?
4
o
O x2.2
o
o 5

Answers
Answer:
The answer is A
Step-by-step explanation:
A rectangle has a width of 9 units and a length of 40 units. What is the length of a diagonal? 31 units 39 units 41 units 49 units can someone help me out Brainly refuses to give me ads for me to get the answers i need and cannot afford rn.
Answers
Answer:
41
Step-by-step explanation:
So basically you need to use the pythagorean thrm. Essentially, the diagonal and the width and length create a triangle, the diagonal being the hypothenuse. So the formula goes as \(\sqrt[]{a^{2} +b^{2} }\). the variable "a" being the length and the variable "b" being the width. So plug it in and there you have your answer!
Answer:
C. 41 units
Step-by-step explanation:
Edge 2021
In 2-3, graph the system of equations to find the solution to the system. Then, use the check step to prove that the solution works in both equations. Show all work
Answers
The system of equations has an infinite number of solutions.
What is an equation?An equation is a mathematical statement that is made up of two expressions connected by an equal sign.
Example:
2x + 4 = 8 is an equation.
We have,
3x + 2y = 6 ____(1)
6x + 4y = 12 _____(2)
Applying the substitution method.
3x + 2y = 6
x = (6 - 2y)/3 in (2)
6 (6 - 2y)/3 + 4y = 12
2 (6 - 2y) + 4y = 12
12 - 4y + 4y = 12
12 = 12
This means,
It has an infinite number of solutions.
Thus,
An infinite number of solutions.
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ9
The complete question is:
Graph the system of equations
3x + 2y = 6
6x + 4y = 12
and find the solution to the system.

Based on the pattern above, how many squares will be in step 4?
15
16
20
25
Answers
T equals blank years. Do not round until the final answer then round to one decimal place as needed

Answers
• Amount invested (,P,): $9500
• Annual interest rate (,r,): 10% = 0.1
\(10\%=\frac{10}{100}=0.1\)• Accumulated amount (,A,): $19000 because it is double the amount invested.
• Time (,t,): ? years.
ExplanationWe replace the know values in the below formula, and we solve for t.
\(\begin{gathered} A=Pe^{rt} \\ 19000=9500e^{0.1t} \\ \text{ Divide by 9500 from both sides} \\ \frac{19000}{9500}=\frac{9500e^{0.1t}}{9500} \\ 2=e^{0.1t} \\ \text{ Apply natural logarithm from both sides} \\ \ln(2)=\ln(e^{0.1t}) \\ \text{ Applt the property }\ln(e^x)=x,\text{ for x > 0} \\ \ln(2)=0.1t \\ \text{ Divide by 0.1 from both sides} \\ \frac{\operatorname{\ln}(2)}{0.1}=\frac{0.1t}{0.1} \\ 6.9\approx t \\ \text{ The symbol }\approx\text{ is read 'approximately'} \end{gathered}\)AnswerThe time it takes to obtain the accumulated amount is approximately 6.9 years.
Precizează felul atributelor din enunțurile de mai jos, analizând părțile de vorbire prin care se exprimă.
Dorința de a mă juca în zăpadă este mare.Avea aerul a nu înțelege.El dovedise un curaj de invidiat.Casele aveau coșuri fumegânde.Nevoia de a o lua din loc din cauza frigului era mare.A lipi bilețele pe un frigider este un mijloc de adus aminte.Fata ținând nasul pe sus a alunecat pe gheață.Blocul de acolo este înalt.Trezitul devreme nu‑mi place.Mersul de colo până colo l‑a obosit.E o vreme brrr!
Answers
Answer:
Step-by-step explanation:
Dorința de a mă juca este mare.
de a (mă) juca - atribut verbal (care dorință?) exprimat prin verb la modul infinitiv;
Avea aerul a nu înțelege.
a nu înțelege - atribut verbal (ce fel de aer?) exprimat prin verb la modul infinitiv;
El dovedise un curaj de invidiat.
de invidiat - atribut verbal (ce fel de curaj?), exprimat prin verb la modul supin.
Casele aveau coșuri fumegânde.
fumegânde - atribut adjectival, exprimat prin verb la gerunziu acordat (cu valoare adjectivală)
Nevoia de a o lua din de a o lua dinloc din cauza frigului era mare.
de a o lua din loc - atribut verbal, exprimat prin locuțiune verbală la modul infinitiv;
A lipi bileţele pe un frigider este un mijloc de adus aminte.
de adus aminte - atribut verbal, exprimat prin locuțiune verbală la modul supin;
Fata ținând nasul pe sus a alunecat pe gheață.
ținând nasul pe sus - atribut verbal, exprimat prin locuțiune verbală la modul gerunziu (neacordat);
Blocul de acolo este înalt.
de acolo - atribut adverbial, exprimat prin adverb de loc;
Trezitul devreme nu-mi place.
devreme - atribut adverbial, exprimat prin adverb de timp;
Mersul de colo până colo l-a obosit.
de colo până colo - atribut adverbial exprimat prin locuțiune adverbială;
E o vreme brrr!
brrr - atribut interjecțional, exprimat prin interjecție.
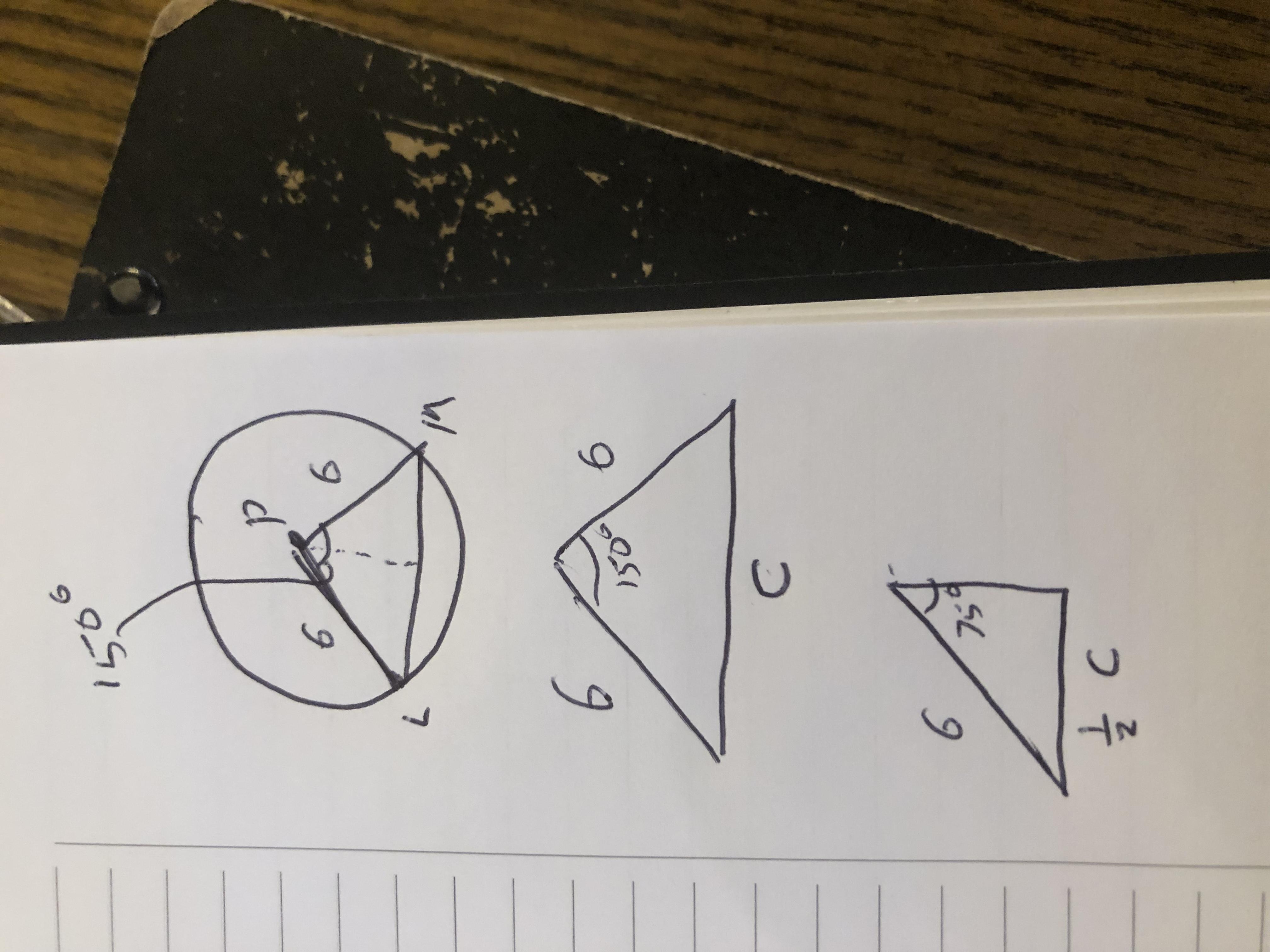
FIND THE LENGTH OF THE CHORD LM

Answers
Answer:
12 sin 75°
Step-by-step explanation:
See the attached images!

solve the equation
a) y''-2y'-3y= e^4x
b) y''+y'-2y=3x*e^x
c) y"-9y'+20y=(x^2)*(e^4x)
Answers
Answer:
a) To solve the differential equation y''-2y'-3y= e^4x, we first find the characteristic equation:
r^2 - 2r - 3 = 0
Factoring, we get:
(r - 3)(r + 1) = 0
So the roots are r = 3 and r = -1.
The general solution to the homogeneous equation y'' - 2y' - 3y = 0 is:
y_h = c1e^3x + c2e^(-x)
To find the particular solution, we use the method of undetermined coefficients. Since e^4x is a solution to the homogeneous equation, we try a particular solution of the form:
y_p = Ae^4x
Taking the first and second derivatives of y_p, we get:
y_p' = 4Ae^4x
y_p'' = 16Ae^4x
Substituting these into the original differential equation, we get:
16Ae^4x - 8Ae^4x - 3Ae^4x = e^4x
Simplifying, we get:
5Ae^4x = e^4x
So:
A = 1/5
Therefore, the particular solution is:
y_p = (1/5)*e^4x
The general solution to the non-homogeneous equation is:
y = y_h + y_p
y = c1e^3x + c2e^(-x) + (1/5)*e^4x
b) To solve the differential equation y'' + y' - 2y = 3xe^x, we first find the characteristic equation:
r^2 + r - 2 = 0
Factoring, we get:
(r + 2)(r - 1) = 0
So the roots are r = -2 and r = 1.
The general solution to the homogeneous equation y'' + y' - 2y = 0 is:
y_h = c1e^(-2x) + c2e^x
To find the particular solution, we use the method of undetermined coefficients. Since 3xe^x is a solution to the homogeneous equation, we try a particular solution of the form:
y_p = (Ax + B)e^x
Taking the first and second derivatives of y_p, we get:
y_p' = Ae^x + (Ax + B)e^x
y_p'' = 2Ae^x + (Ax + B)e^x
Substituting these into the original differential equation, we get:
2Ae^x + (Ax + B)e^x + Ae^x + (Ax + B)e^x - 2(Ax + B)e^x = 3xe^x
Simplifying, we get:
3Ae^x = 3xe^x
So:
A = 1
Therefore, the particular solution is:
y_p = (x + B)e^x
Taking the derivative of y_p, we get:
y_p' = (x + 2 + B)e^x
Substituting back into the original differential equation, we get:
(x + 2 + B)e^x + (x + B)e^x - 2(x + B)e^x = 3xe^x
Simplifying, we get:
-xe^x - Be^x = 0
So:
B = -x
Therefore, the particular solution is:
y_p = xe^x
The general solution to the non-homogeneous equation is:
y = y_h + y_p
y = c1e^(-2x) + c2e^x + xe^x
c) To solve the differential equation y" - 9y' + 20y = x^2*e^4x, we first find the characteristic equation:
r^2 - 9r + 20 = 0
Factoring, we get:
(r - 5)(r - 4) = 0
So the roots are r = 5 and r = 4.
The general solution to the homogeneous equation y" - 9y' + 20y = 0 is:
y_h = c1e^4x + c2e^5x
To find the particular solution, we use the method of undetermined coefficients. Since x^2*e^4x is a solution to the homogeneous equation, we try a particular solution of the form:
y_p = (Ax^2 + Bx + C)e^4x
Taking the first and second derivatives of y_p, we get:
y_p' = (2Ax + B)e^4x + 4Axe^4x
y_p'' = 2Ae^4x +
Please show step by step of working out the value of r for which is A minimum and calculate the minimum surface area of the container.
The total surface area, Acm^2, of each container is modelled by function A= πr^2+100/r.
(remember to use the derivative to show you have found the minimum)

Answers
Answer:
A = 59.63cm^2
Step-by-step explanation:
You have the following function for the surface area of the container:
\(A=\pi r^2+\frac{100}{r}\) (1)
where r is the radius of the cross sectional area of the container.
In order to find the minimum surface are you first calculate the derivative of A respect to r, to find the value of r that makes the surface area a minimum.
\(\frac{dA}{dr}=\frac{d}{dr}[\pi r^2+\frac{100}{r}]\\\\\frac{dA}{dr}=2\pi r-\frac{100}{r^2}\) (2)
Next, you equal the expression (2) to zero and solve for r:
\(2\pi r-\frac{100}{r^2}=0\\\\2\pi r=\frac{100}{r^2}\\\\r^3=\frac{50}{\pi}\\\\r=(\frac{50}{\pi})^{1/3}\)
Finally, you replace the previous result in the equation (1):
\(A=\pi (\frac{50}{\pi})^{2/3}+\frac{100}{(\frac{50}{\pi})^{1/3}}}\)
\(A=59.63\)
The minimum total surface area is 59.63cm^2
1. Tim wants air conditioning in his room. The air conditioner costs $40. Each day the
electricity costs $1. Write an expression that can be used to find the cost to run the air
conditioner for d days.
Answers
Answer:
the answer/expression you require is 40 - 1 = 1 day x - 1 = day 2 (repeat day 2 forever
Step-by-step explanation:
i say this because - 40 for the air conditioner and if it’s - 1 for electricity a day then unless your buying an air conditioner every day i don’t think you,l be repeating day 1 every day
:D
Find the exact value of csc 5pi/6
Answers
Answer:
csc 2 (csc \(\frac{5\pi}{6}\) = csc 150 = csc 30 = csc 2)
Step-by-step explanation:
csc \(\frac{5\pi}{6}\) is in the 2nd Quadrant where only sin, and csc are positive.
csc \((\frac{5\pi}{6})=csc (\pi -(\frac{5\pi}{6}))=csc(\frac{5\pi}{6})\)
but csc \(\frac{5\pi}{6}\) = \(\frac{1}{sin (\pi/6)} = \frac{1}{sin 30} = \frac{1}{1/2} =2\)
What is the common ratio for this geometric sequence? 27, 9,3,1,..
Answers
Answer:
1/3
Step-by-step explanation:
a1=27
a2=9
common ratio=a2/a1=9/27=1/3
pls help me
In the figure, and .
(a)Write an equation to find . Make sure you use an "" sign in your answer.
(b)Find the degree measure of each angle.

Answers
Step-by-step explanation:
2x + x + 57 = 90
3x = 33
x = 11
m1 = 2 × 11 = 22°
m2 = 11 + 57 = 68°
check: 22 + 68 = 90
HIIIIIII ILL MARK BRAINLIEST
is this correct?

Answers
Answer:
No, it isn't.
Step-by-step explanation:
The point on y = 5 should be on y = 7, and the point on x = 5 should be on x = 7. The attachment shown is what the graph should look like.

HOW DO I SIMPLIFY? I WILL MARK YOU BRAINLIEST! AND EXPLAIN
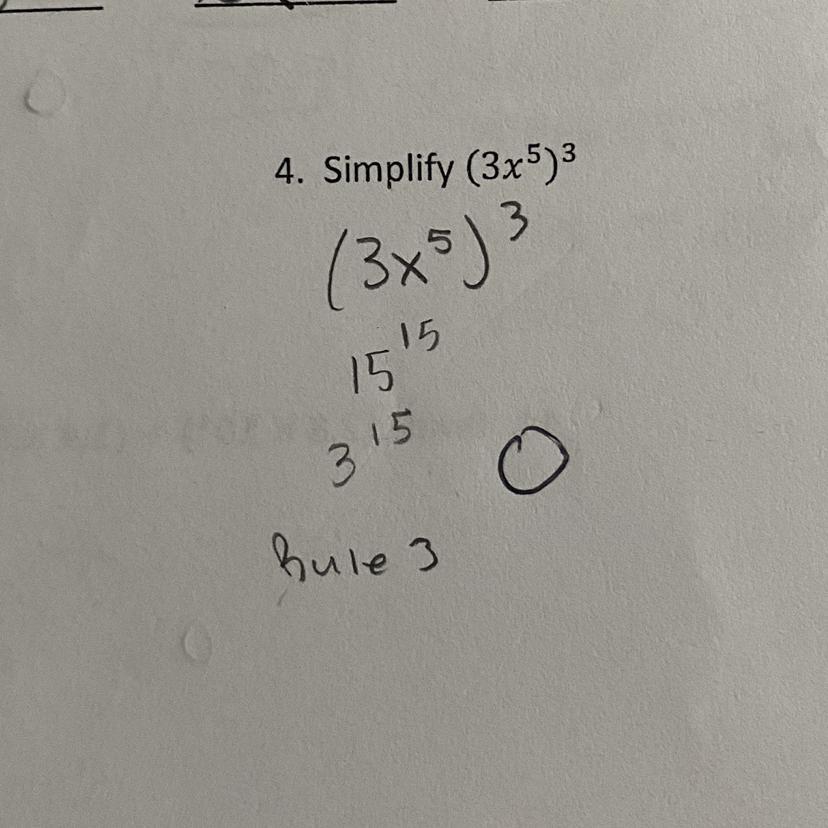
Answers
Answer:
This is how you simplify it.

Answer:
Step-by-step explanation:
(3x⁵)^3
= {3x}^(15) (According to rule)
Answer = (3x)^(15)
what is the range of the function f (x) = lxl +5?
Answers
The range of the function f(x)= IxI+5 is x+5 for x>=0 and -x+5 for x<0.
Given that the function is f(x)=IxI+5.
We are required to find the range of the function.
Function is relationship between two or more variables expressed in equal to form. In a function each value of x must have a corresponding value of y. The value of x is known as domain of the function and the value of y is known as codomain of the function. Range of a function is a limit of values in which the values of function lies.
Function is f(x)= IxI+5
We know that IxI=x for x>=0 and -x<0.
We have to just put the value of IxI in f(x) to get the range of function.
f(x)=x+5 for x>=0 and -x+5 for x<0.
Hence the range of the function f(x)= IxI+5 is x+5 for x>=0 and -x+5 for x<0.
Learn more about range at https://brainly.com/question/26098895
#SPJ1
Which shows two possible values for a number represented by the point?
0
1
7 and 3
AN
27 and 1
2
2 and 2
O 2 and 2
Answers
Answer:
b
Step-by-step explanation:
Simplify: Simplify: StartRoot StartFraction 27 x Superscript 12 Baseline Over 300 x Superscript 8 Baseline EndFraction EndRoot
Answers
The solution of the given expression is 9*\(x^{4}\)/100.
GIven an expression equal to 27\(x^{12}\)/300\(x^{8}\).
We have to simplify the expression in which variable comes only once.
Expression is combination of numbers ,symbols, fraction, coefficients, indeterminants,determinants, etc. It is mostly not found in equal to form. It expresses a relationship between variables.
The given fraction is 27\(x^{12}\)/300\(x^{8}\).
When we observe we find that in numerator x has large power and denominator x has small power as compared to power in numerator. So we will deduct the powers so that they will give only one power to us.
=27\(x^{4}\)/300
Now divide numerator an denominator by 3.
=9\(x^{4}\)/300
Hence the expression 27\(x^{12} /300x^{8}\) will look like \(9x^{4} /100\) after simplifying.
Learn more about expression at https://brainly.com/question/723406
#SPJ1
Answer:
\(Simplify:\sqrt\frac{27x^{12} }{300x^{8} }\)
\(O \frac{9}{100}x^{4}\)
✔ \(\frac{3}{10} x^{2}\)
\(O \frac{27}{300} x^{4}\)
\(O\frac{9}{10} x^{2}\)
Set the mean and standard deviation to 0 and 5 , respectively. Approximately 5% of the area under the normal curve lies to the right of 8.2 . Consider what would happen if you were to change the mean to 50 and keep the standard deviation at 5 . Can you predict the new value for which approximately 5% of the area under the normal curve lies to the right of this value? Enter your answer accurate to one decimal place.
Answers
Using z-scores and the normal distribution, it is found that the new value would be of 58.2.
In a normal distribution with mean and standard deviation , the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
It measures how many standard deviations the measure is from the mean. After finding the z-score, we look at the z-score table and find the p-value associated with this z-score, which is the percentile of X, which is the area to the left of Z under the normal curve.The area to the right of Z is 1 subtracted by the p-value of Z.In this problem:
Mean of 50 and standard deviation of 5, thus \(\mu = 50, \sigma = 5\).Area to the right of 0.05, thus Z with a p-value of 1 - 0.05 = 0.95, thus \(Z = 1.645\).We have to find the value of X, then:
\(Z = \frac{X - \mu}{\sigma}\)
\(1.645 = \frac{X - 50}{5}\)
\(X - 50 = 1.645(5)\)
\(X = 58.2\)
A similar problem is given at https://brainly.com/question/15583760
Hello please help I will give brainliest!

Answers
Answer:
D
Step-by-step explanation:
Please help me please I will give brainliest!

Answers
Answer:
3) Because the run go by 4 and the rise go up by 2
Step-by-step explanation:
What is the best estimate for the value of the expression?
34
8
16
3
14
9.
-3
-21
O7
Answers
Answer: 8 is the anwser
Step-by-step explanation:
What is the surface area of the cylinder with height 2 m and radius 2 m? round your answer to the nearest thousandth.
Answers
The surface area of the cylinder with height 2 m and radius 2 m is: 50.265 m².
What is the Surface Area of a Cylinder?The surface area of a cylinder can be calculated by adding the area of the top and bottom circles (which have the same radius) to the area of the curved side (which is a rectangle that has a height equal to the height of the cylinder and a width equal to the circumference of the circle).
The formula for the surface area of a cylinder is:
Surface Area = 2πr² + 2πrh
Where:
π (pi) = 3.14
r is the radius of the circular base of the cylinder
h is the height of the cylinder
Given the following:
Height (h) = 2 m
Radius (r) = 2 m
Therefore, we have:
Surface area = 2πrh + 2πr² = 2·π·2·2 + 2·π·22 ≈ 50.265 m²
Learn more about surface area of cylinder on:
https://brainly.com/question/27440983
#SPJ1
A 2 1/2 pound bag of grass seed covers 1/8 of an acre. How much grass seed is needed for 1 acre?
Answers
Answer:
it needs 234 grass seeds for the acre
If f(x)=3x-2 and g(x)=2x+1, find (f-g)(x)
A. 5x-3
B. 5x-1
C. X-3
D. 3-x
I need step by step explanation please
Answers
Answer:
B
Step-by-step explanation:
3x - 2 + 2x + 1
5x - 1
En una plaza Lucio camina en tramos rectos, a partir del asta bandera, en un punto cambia la dirección girando 150º a su izquierda, avanza 64 metros y se detiene. Para regresar al asta tiene que girar 75º a la izquierda, ¿A qué distancia se encuentra del punto inicial?
Answers
Lucio is 64 meters from the starting point.
How to solveThe square has four sides of equal length, so Lucio has walked half the length of one side.
To return to the starting point, he needs to walk the other half of the side, which is 64 meters.
The angle Lucio turns is irrelevant, as long as he turns 180 degrees in total.
With this in mind, it can be seen that based on the parameters and the conditions, Lucio is 64 meters from the starting point because the angle to which he turns is irrelevant.
Read more about angles here:
https://brainly.com/question/25716982
#SPJ1
The question in English:
In a square Lucio walks in straight sections, starting from the flagpole, at one point he changes direction turning 150º to his left, advances 64 meters and stops. To return to the pole you have to turn 75º to the left. How far are you from the starting point?
HELP I WILL MARK BRAINLIEST!!!
Sammy deposited $2 into a savings account. She then saves $1 per week. Write a linear function for this situation where x = the number of weeks and y = the total amount of money in the account.

Answers
Answer:
\(y = 2 + x\)
Step-by-step explanation:
x=0, y=2
x=1, y=3
x=2, y=4
x=3, y=5
NO LINKS!! Express the statement as an inequality. Part 4

Answers
Answer:
A) b>0 B) s<0 C) w≥-6
Step-by-step explanation:
A) greater than means >
B) less than means <
C) greater of equal means ≥
Answer:
(a) b > 0
(b) s ≤ 0
(c) w ≥ -6
Step-by-step explanation:
Symbol notation
< means "less than".> means "greater than".≤ means "less than or equal to".≥ means "greater than or equal to".= means "equals".A negative real number is any real number that is less than zero.
A positive real number is any real number that is greater than zero.
Zero is neither positive nor negative.
Part (a)If b is positive then it is greater than zero:
b > 0Part (b)Nonpositive means not positive, so either negative or equal to zero.
If s is nonpositive then it is less than or equal to zero:
s ≤ 0Part (c)w is greater than or equal to -6:
w ≥ -69. Kyoko plans to put a new wood floor in her den, which is shown in the floor plan.
a. What is the area of the floor?
b. At a cost of $11 per square foot, how much will it
cost to put down the new floor?
c. Kyoko plans to put a rectangular area rug in the
room. The rug will be large enough so that only
a 2-foot wide section of the wood floor will be
exposed on each side. Find the dimensions of the
area rug.
d. What is the area of the area rug?
Den
17 ft x 14.5 ft
e. Find the area of the wood floor that will be exposed once the area rug is laid down.
Answers
a.) The area of the floor = 246.5ft²
b.) The amount that it will cost to put down the new floor would be = $2,711.5
C.) The new dimensions of the area rug would be= Length= 21ft, width = 18.5 ft.
d.) The area of the area rug would be = 388.5ft²
How to calculate the area of the floor?For question a.)
The floor has a rectangular shape. The area of a rectangle = length×width
area of the floor= 17×14.5
= 246.5ft²
For question b.)
For a square foot(1ft²) = $11
246.5ft² = 246.5×11 = $2,711.5
For question c.)
Since the rug will be extended by 2ft at each side, the new dimensions would be:
length = 2+2+17 = 21ft
width = 2+2+14.5 = 18.5ft
For question d.)
The area of the floor with the new dimensions = 21×18.5 = 388.5ft²
Learn more about area here:
https://brainly.com/question/25292087
#SPJ1

What does the y-intercept of the line tell you about the situation?
Please answer this quickly it’s due in 10min

Answers
The y-intercept of the linear function means that her initial distance from the finish line is of 10 kilometers.
How to define a linear function?The slope-intercept equation for a linear function is presented as follows:
y = mx + b
In which:
m is the slope.b is the y-intercept.The graph crosses the y-axis at y = 10, hence the intercept b is given as follows:
b = 10.
The y-values represent the distance in the context of this problem, hence the initial distance is of 10 km.
More can be learned about linear functions at https://brainly.com/question/15602982
#SPJ1