A train leaves the station every 12 minutes, a train leave the station every 18 minutes, at 8am a bus and a train leave the station at the same time, when is the next time the bus and train will leave at the same time
Answers
Answer: 8:36AM
Step-by-step explanation:
12 18
24 36
36
LCM or least common denominator to solve
Answer:
8 : 36 am
Step-by-step explanation:
we are trying to find:
train : 12
bus : 18
(the next time that 12 and 18 will both evenly go into a number/start at the same time will be the "lowest common multiple")
the lowest common multiple can actually be found fairly easily.
most people assume that finding the LCM (lowest common multiple) is a matter of guesswork - it's not
We can find the LCM by multiplying the absolute values of two numbers, and dividing by their GCD (greatest common divisor- the largest number that both can be evenly divided by).
12 and 18 share a GCD of 6.
So, we multiply 12 × 18 = 216
and divide by 6 216 / 6 = 36
The next time that the bus and train leave the station at the same time will be in 36 minutes--which will be 8 : 36 am.
Related Questions
reduce 12/16 to simplest terms
Answers
Answer: 3/4
Step-by-step explanation:
Find the GCD (or HCF) of numerator and denominator
GCD of 12 and 16 is 4
Divide both the numerator and denominator by the GCD
12 ÷ 4
16 ÷ 4
Reduced fraction: 3/4
Therefore, 12/16 simplified to lowest terms is 3/4.
Answer:.
Step-by-step explanation:
Which of the following statements involve inferential statistics as opposed to descriptive statistics?
a. A total of 4,785 people
b. The FAA
c. a class of fifty stats students
d. the city business office reported
e. based on a sample of 500 subscribers
Answers
The statement that involves descriptive statistics is -
Option A) The Alcohol, Tobacco, and Firearms Department reported that Houston had 1,791 registered gun dealers in 1997.
What are two categories of field statistics?
There are two categories of field statistics. Descriptive and inferential statistics. Both of them help analysts to make sense of row after row data.
Descriptive statistics presents quantifiable descriptions in a simple way. Inferential statistics is used to draw conclusions that go beyond the raw data only. It is used in making judgments, inferences to deeper general conditions.
The Alcohol, Tobacco, and Firearms Department reported that Houston had 1,791 registered gun dealers in 1997.
Descriptive statistics are useful in describing the basic features of the data being analyzed. They simply provide what the raw data shows. They simplify huge amounts of data sensibly and make it presentable in a manageable form.
With regard to the question, raw data is available stating that the registered gun dealers were 1791 in 1997. It, therefore, involves descriptive statistics.
Therefore, the correct answer is option A.
To learn more about field statistics from the given link
https://brainly.com/question/14724376
#SPJ4
Which of the following statements involve descriptive statistics as opposed to inferential statistics?
A) The Alcohol, Tobacco, and Firearms Department reported that Houston had 1,791 registered gun dealers in 1997.
B) Based on a survey of 400 magazine readers, the magazine reports that 45% of its readers prefer double-column articles.
C) The FAA samples 500 traffic controllers in order to estimate the percent retiring due to job-stress-related illness.
D) Based on a sample of 300 professional tennis players, a tennis magazine reported that 25% of the parents of all professional tennis players did not play tennis.
At many bakeries, there are deals that if you buy twelve donuts, you get a thirteenth one at a discount. Sometimes "13" items is called a baker's dozen. I One store is advertising: Donuts! $1.05 individually, or $13 per baker's dozen. They want to program their cash register to be able to show the exact price for any number of donuts. You will help them by producing a data table, a graph and an algorithm. You will: 1. Fill in and expand the data table 2. Make a scatter plot to show the pattern visually. This means to plot an (x,y) point for every row in the data table. For example the first point can be (1, 1.05) 3. Develop an algorithm to find the cost for any number of donuts. Note: An algorithm is like a set of instructions to solve a problem. They are useful for telling computers or people exactly how to do something. For example, here is an algorithm that finds 15% of a number: Step 1: take any number, callit N.
Answers
Table
Number of donuts Price
1 $1.05
2 $ 2.1
3 $3.15
4 $4.2
5 $5.25
6 $6.3
10 $10.5
slope = (10.5 - 1.05) / 10 - 1
= 9.45 / 9
= 1.05
Equation
y - 10.5 = 1.05 (x - 10)
y = 1.05x - 10.5 + 10.5
y = 1.05x
For 40 donuts
y = 1.05(40)
y = $42

GEOMETRY!! Will give brainliest which one is better please explain

Answers
Solve for x.
2x + 9 = 33
A. x = 7.5
B. x = 12
C. x = 21
D. x = 84
Answers
Solve for x.
2x + 9 = 33
2x = 24
x = 12
A. x = 7.5
B. x = 12
C. x = 21
D. x = 84
Answer:
\(2x + 9 = 33 \\ 2x = 33 - 9 \\ 2x = 24 \\ x = \frac{24}{2} \\ x = 12\)
Among all pairs of numbers whose sum is 24, find a pair whose product is as large as possible. Show the work(the steps)! Write an equation of the corresponding quadratic function. How parabola opens? What is the maximum product? Does this function has a maximum value or the minimum value? Explain. Graph the function and upload the image.
Answers
The pair of numbers that yields the maximum product when their sum is 24 is (12, 12), and the maximum product is 144. The corresponding quadratic function is P(x) = -x^2 + 24x, and the parabola opens downwards.
To find a pair of numbers whose sum is 24 and whose product is as large as possible, we can use the concept of maximizing a quadratic function.
Let's denote the two numbers as x and y. We know that x + y = 24. We want to maximize the product xy.
To solve this problem, we can rewrite the equation x + y = 24 as y = 24 - x. Now we can express the product xy in terms of a single variable, x:
P(x) = x(24 - x)
This equation represents a quadratic function. To find the maximum value of the product, we need to determine the vertex of the parabola.
The quadratic function can be rewritten as P(x) = -x^2 + 24x. We recognize that the coefficient of x^2 is negative, which means the parabola opens downwards.
To find the vertex of the parabola, we can use the formula x = -b / (2a), where a = -1 and b = 24. Plugging in these values, we get x = -24 / (2 * -1) = 12.
Substituting the value of x into the equation y = 24 - x, we find y = 24 - 12 = 12.
So the pair of numbers that yields the maximum product is (12, 12). The maximum product is obtained by evaluating the quadratic function at the vertex: P(12) = 12(24 - 12) = 12(12) = 144.
Therefore, the maximum product is 144. This quadratic function has a maximum value because the parabola opens downwards.
To graph the function, you can plot several points and connect them to form a parabolic shape. Here is an uploaded image of the graph of the quadratic function: [Image: Parabola Graph]
For more such question on function. visit :
https://brainly.com/question/11624077
#SPJ8
3.
Find the indicated Matrix, if possible. Show and explain your work.
3A +B
a={5,2}
b={7 1}
{5 0}
Answers
The matrix 3A + B cannot be defined, as 3A and B have different dimensions, hence they cannot be added.
What is the matrix in math?When we add two matrices, we add the equivalent elements, that is, the elements at the same position in each matrix, hence for the addition of matrices they should have the same dimensions.
The matrices are given by:
3a: 3[5 2]' = [15 6].
b = [7 1;5 0].
With the ; indicating a new line, hence they have different dimensions(A 2 x 1 and B 2 x 2), so the matrix 3A + B cannot be defined.
Therefore, the matrix 3A + B cannot be defined, as 3A and B have different dimensions, hence they cannot be added.
Learn more about matrix, here:
https://brainly.com/question/28367773
#SPJ1
What is 504 times 83
Answers
Answer:
41832
Step-by-step explanation:
if there are 5 boys and 7 girls, write the ratio of girls to total students
Answers
Answer:
7:12
Step-by-step explanation:
boys=5
girls=7
total=boys+girls
12=5+7
girls:total
7:12
Lesson 4 problem solving practice
Answers
Answer:
what is your question?
Step-by-step explanation:
Find the amount in an account where $500 is invested at 2.5% compounded continuously for period of 10 years
Answers
Hi
500 *1.025^10 ≈ 640.04
20 points and brainliest
I’m in quiz in need it asap
Number 4

Answers
Answer and step-by-step explanation:
The polar form of a complex number \(a+ib\) is the number \(re^{i\theta}\) where \(r = \sqrt{a^2+b^2}\) is called the modulus and \(\theta = tan^-^1 (\frac ba)\) is called the argument. You can switch back and forth between the two forms by either remembering the definitions or by graphing the number on Gauss plane. The advantage of using polar form is that when you multiply, divide or raise complex numbers in polar form you just multiply modules and add arguments.
(a) let's first calculate moduli and arguments
\(r_1 = \sqrt{(-2\sqrt3)^2+2^2}=\sqrt{12+4} = 4\\ \theta_1 = tan^-^1(\frac{2}{-2\sqrt3}) =-\pi/6\\r_2=\sqrt{1^2+1^2}=\sqrt2\\ \theta_2 = tan^-^1(\frac 11)= \pi/4\)
now we can write the two numbers as
\(z_1=4e^{-i\frac \pi6}; z_2=e^{i\frac\pi4}\)
(b) As noted above, the argument of the product is the sum of the arguments of the two numbers:
\(Arg(z_1\cdot z_2) = Arg(z_1)+Arg(z_2) = -\frac \pi6 + \frac \pi4 = \frac\pi{12}\)
(c) Similarly, when raising a complex number to any power, you raise the modulus to that power, and then multiply the argument for that value.
\((z_1)^1^2=[4e^{-i\frac \pi6}]^1^2=4^1^2\cdot (e^{-i\frac \pi6})^1^2=2^2^4\cdot e^{-i(12)\frac\pi6}\\=2^2^4 e^{-i\cdot2\pi}=2^2^4\)
Now, in the last step I've used the fact that \(e^{i(2k\pi+x)} = e^i^x ; k\in \mathbb Z\), or in other words, the complex exponential is periodic with \(2\pi\) as a period, same as sine and cosine. You can further compute that power of two with the help of a calculator, it is around 16 million, or leave it as is.
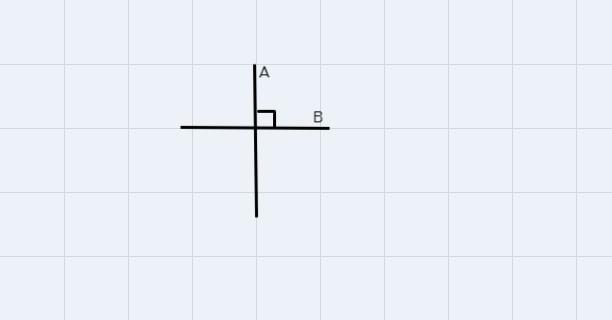
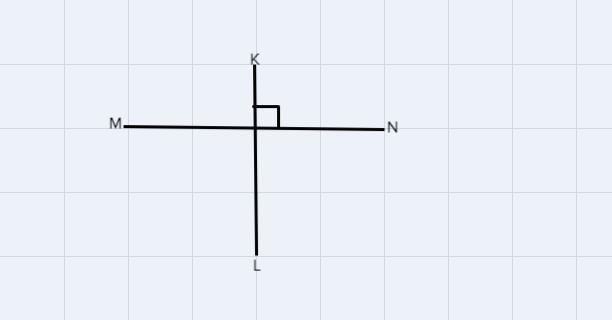
wich time of line are shown in the figure
Answers
Solution
Step 1
Two distinct lines intersecting each other at 90° or at right angles are perpendicular to each other.
Hence apply this to question 8 the type of lines shown in the figure is perpendicular lines. Option C
Step 2
To explain this as stated above line A and line B intersect each other at a right angle hence line A and B are perpendicular lines. The line segments are seen below.
Are 20,30, and 16 the sides of a right triangle? Please show workkk
Answers
An H0-scale model railroad engine is 9 inches long. The H0 scale is 87 feet to 1 foot. How long is a real engine?
Answers
The real engine is 65.25 feet long
How to determine the length?The scale is given as:
Scale = 87 feet to 1 foot
The scale length is given as
Scale length = 9 inches
Convert inches to feet
Scale length = 9/12 feet
The actual length is then calculated as:
Actual = 87 * 9/12 feet
Evaluate
Actual = 65.25 feet
Hence, the real engine is 65.25 feet long
Read more about scale ratios at:
https://brainly.com/question/16192120
#SPJ1
Camila has 6 bags of candy. She can pour 1/3 of a bag of candy into a bowl. How many bowls of candy can Camila make in all?
Answers
Answer:
18 Bowls of Candy
Step-by-step explanation:
Camila has 6 bags of candy, and she can pour 1/3 of a bag into a bowl. To determine how many bowls of candy she can make in total, we need to divide the total amount of candy by the amount of candy per bowl.
Since Camila can pour 1/3 of a bag into a bowl, it means she can make 3 bowls of candy with a full bag.
Now, we can calculate the total number of bowls of candy:
Total bowls of candy = (Number of bags) x (Bowls per bag)
Total bowls of candy = 6 bags x 3 bowls per bag
Total bowls of candy = 18 bowls
Therefore, Camila can make a total of 18 bowls of candy with her 6 bags of candy.
In the figure below, ABDC, EFHG, and ASHY are all squares; AB=1, EF=1, and AY=5.
What is the area of quadrilateral DYES?

Answers
Answer:
15 unit²Step-by-step explanation:
ASHY is the square with the side of 5.
DYES is the rhombus since all sides are same and diagonals are perpendicular.
The area of the rhombus is the difference of the area of the big square and the sum of small squares and triangles:
A = 5² - (2*1² + 4*(1/2*1*4)) = 25 - (2 + 8) = 25 - 10 = 15Answer:
15 square units
Step-by-step explanation:
its correct, trust me
Annette has 3 hours to spend training for an upcoming race. She completes her training by running full speed the distance of the race and walking back the same distance to cool down. If she runs at a speed of 9mph and walks back at a speed of 3mph , how long should she plan to spend walking back?
Answers
Answer:
Annette should plan to spend 2.25 hours walking back.
Step-by-step explanation:
To solve this problem, we can use the formula:
Time = Distance / Speed
Let's assume the distance of the race is D miles.
Annette spends her time running the distance of the race, which takes:
Time running = D / 9 hours
She then walks back the same distance, which we need to find the time for:
Time walking = D / 3 hours
Since Annette has a total of 3 hours for her training, the sum of the running time and walking time should equal 3 hours:
D / 9 + D / 3 = 3
To simplify the equation, we can multiply all terms by 9 to eliminate the denominators:
D + 3D = 27
Combining like terms:
4D = 27
Dividing both sides of the equation by 4:
D = 6.75
So, the distance of the race is 6.75 miles.
To find the time Annette should spend walking back, we substitute the distance into the time-walking formula:
Time walking = D / 3 = 6.75 / 3 = 2.25 hours
Therefore, Annette should plan to spend 2.25 hours walking back.
Question 4 O Mark this question Megan was conducting a study to determine if there was a relationship between eating a whole foods diet and general overall health. For her study Megan's null hypothesis was that a whole foods diet would not have any impact on general health. Megan's alternate hypothesis was that eating a whole foods diet would cause improvements in health. If Megan completed her study, which of the following statements would indicate a Type I error? Megan's results show that a whole foods
Answers
Type I error is "Megan's results show significant improvements in health associated with a whole foods diet."
A Type I error occurs when the null hypothesis is rejected, even though it is true.
In this case, the null hypothesis states that a whole foods diet would not have any impact on general health.
Therefore, a Type I error would occur if Megan's results show significant improvements in health associated with a whole foods diet.
This means that Megan would reject the null hypothesis and conclude that a whole foods diet does have an impact on general health, even though it is not true.
So, the statement that would indicate a Type I error is "Megan's results show significant improvements in health associated with a whole foods diet."
To learn more on Null hypothesis click:
https://brainly.com/question/30821298
#SPJ1
#4
Write an equation in slope-intercept
form to represent the line
perpendicular to 6y = 9 - x with
y-intercept 2
O y = -6x + 2
O y = 2x + 9
Answers
Answer:
A, y= -6x + 2
Step-by-step explanation:
1. Put the equation into slope intercept form
6y = 9 - x
y= -1/6x + 9/6
The slope of equation 1 is -1/6
2. A perpendicular line is the inverse slope of our firsy equation. (-1/6)^-1 = -6.
3. The y intercept of a line in slope intercept form is the b value in the equation as written:
y=mx+b
Therefore, if m=-6 and b=2, our equation is
y= -6x + 2
100 POINTS PLEASE HELP ME ALGEBRA

Answers
The range of the graph of the exponential function is (b) {y | y > 0}
Calculating the range of the graphFrom the question, we have the following parameters that can be used in our computation:
The graph of the exponential function
The rule of an exponential function is that
The domain is the set of all real numbers
This means that the input value can take all real values
However, the range is always greater than the constant term
From the graph, the constant term is 0
So, the range is y > 0
Read more about range at
brainly.com/question/27910766
#SPJ1
-(4-x)=3/4(x-6) i need help pls
Answers
Solve for x by simplifying both sides of the equation, then isolating the variable.
x=−2
hope this is what your looking for
Answer:
x = -2
Step-by-step explanation:
\(-4+x=\frac{3}{4}x-\frac{9}{2}\)
\(\mathrm{Add\:}4\mathrm{\:to\:both\:sides}\)
\(-4+x+4=\frac{3}{4}x-\frac{9}{2}+4\)
\(Simplify\)
\(x=-\frac{1}{2}+\frac{3}{4}x\)
\(\mathrm{Subtract\:}\frac{3}{4}x\mathrm{\:from\:both\:sides}\)
\(x-\frac{3}{4}x=-\frac{1}{2}+\frac{3}{4}x-\frac{3}{4}x\)
\(\frac{1}{4}x=-\frac{1}{2}\)
\(\mathrm{Multiply\:both\:sides\:by\:}4\)
\(4\cdot \frac{1}{4}x=4\left(-\frac{1}{2}\right)\)
\(x=-2\)
~lenvy~
Which ordered pair is a solution to the system of linear equations? x + 4y = 3 y = −4x − 3 (1, 1) (1, −1) (−1, 1) (−1, −1)
Answers
Answer:
(-1,1)
Step-by-step explanation:
Solve for the first variable in one of the equations, then substitute the result into the other equation.
equation form:
x=-1, y=1
have a great day and thx for your inquiry :)
By substituting each of the provided options into the given system of linear equations, it is revealed that the ordered pair (-1, 1) is a valid solution for both the equations.
The correct answer is (-1, 1)
In mathematics, a system of linear equations consists of multiple linear equations with the same variables. These equations describe various relationships among these variables, typically representing lines in a multi-dimensional space. Solving such systems involves finding values for the variables that satisfy all equations simultaneously. Methods like substitution, elimination, or matrix algebra can be used to solve these systems. These systems are fundamental in fields like physics, engineering, economics, and computer science for modeling and solving real-world problems involving multiple interconnected variables.
We can solve this problem by substituting values from the given options into the equations and checking for which option both equations are valid. The system of linear equations is: x + 4y = 3 and y = -4x - 3.
Option (1, 1): For x = 1 and y = 1, our system becomes 1 + 4*1 = 5 and y = -4*1 - 3 = -7. Both do not hold true.Option (1, -1): For x = 1 and y = -1, our system becomes 1 + 4*-1 = -3 and y = -4*1 - 3 = -7. Both do not hold true.Option (-1, 1): For x = -1 and y = 1, our system becomes -1 + 4*1 = 3 (correct) and y = -4*-1 - 3 = 1 (correct). Thus, option (-1, 1) is a solution to the system of equations.Option (-1, -1): For x = -1 and y = -1, our system becomes -1 + 4*-1 = -5 and y = -4*-1 - 3 = 1. Both do not hold true.Therefore, the ordered pair that is a solution to the system of linear equations is (-1, 1).
Learn more about System of Linear Equations here:
https://brainly.com/question/33609849
#SPJ2
HELP ME PLEASE
what is the first term of the sequence with the nth term rule: 7n - 10
Answers
Answer:
1st term= -3
Step-by-step explanation:
You are already given an expression for nth term
so all you do is plug in 1 for n to get the first term and so forth
t=7(1) -10
t=7-10
t=-3
If g(x) = f(x) + k, what is the k value?

Answers
Answer:
If g(x) = f(x) + k, what is the k value?
The answer The value of k is 6
The time between arrivals of customers at an automatic teller machine is an exponential random variable with a mean of 4 minutes. Round yours answers to 4 decimal places. (a) What is the probability that more than three customers arrive in 10 minutes
Answers
Answer:
0.7788 = 77.88% probability that more than three customers arrive in 10 minutes
Step-by-step explanation:
Exponential distribution:
The exponential probability distribution, with mean m, is described by the following equation:
\(f(x) = \mu e^{-\mu x}\)
In which \(\mu = \frac{1}{m}\) is the decay parameter.
The probability that x is lower or equal to a is given by:
\(P(X \leq x) = \int\limits^a_0 {f(x)} \, dx\)
Which has the following solution:
\(P(X \leq x) = 1 - e^{-\mu x}\)
The probability of finding a value higher than x is:
\(P(X > x) = 1 - P(X \leq x) = 1 - (1 - e^{-\mu x}) = e^{-\mu x}\)
In this question, we have that:
The time between arrivals of customers at an automatic teller machine is an exponential random variable with a mean of 4 minutes, and we have three customers, which means that \(m = 3*4 = 12, \mu = \frac{1}{12} = 0.0833\)
(a) What is the probability that more than three customers arrive in 10 minutes
This is P(X > 3). So
\(P(X > 3) = e^{-0.0833*3} = 0.7788\)
0.7788 = 77.88% probability that more than three customers arrive in 10 minutes
Find the missing side b. Round your answer to the nearest tenth if needed

Answers
Answer:
b = 20
Step-by-step explanation:
This is a right triangle with the ratio of the given sides being ...
15 : 25 = 3 : 5
This means it is a 3:4:5 right triangle. The side ratios are ...
a : b : c = 3 : 4 : 5 = 15 : 20 : 25
The missing side length is b = 20.
__
You can also figure this using the Pythagorean theorem.
c² = a² + b²
25² = 15² +b²
625 -225 = b² = 400
b = √400 = 20
The missing side length is 20.
1. You pay $10 to play the following game of chance. There is a bag containing 12 balls, five are red, three are
green and the rest are yellow. You are to draw one ball from the bag. You will win $14 if you draw a red ball and
you will win $12 is you draw a yellow ball. How much do you expect to win or loss if you play this game 100
times?
O a
-2.40
Ob -1.67
Oc -16.67
Od -24.00
Answers
Answer:
Step-by-step explanation:
Which measures are the sides lengths of a right triangle?
a)4cm 12cm 8cm
b)5cm 12cm 10cm
c)16cm 4cm 6cm
d)30cm 12cm 6cm
Answers
Answer:
b)
Step-by-step explanation:
a) 4+12>8
12+8>4
4+8=12
NO
b) 5+12>10
10+5>12
12+10>5
YES
c) 16+4>6
6+4<16
NO
d) 30+12>6
12+6<30
NO
Find the complete factored form of the
polynomial :
-8m²n-7m² nª
Enter the correct answer.
Answers
The polynomial -8m²n - 7m²n can be factored using the common factor -m²n. The complete factored form of the polynomial is (-m²n) (8 + 7a).
To find the complete factored form of the polynomial -8m²n - 7m²n, we can factor out common terms from both the terms. The common factor in the terms -8m²n and -7m²n is -m²n. We can write the polynomial as:
-8m²n - 7m²n = (-m²n) (8 + 7a)
Therefore, the complete factored form of the polynomial -8m²n - 7m²n is (-m²n) (8 + 7a). This expression represents the original polynomial in a multiplied form. We can expand this expression using distributive law to verify that it is equivalent to the original polynomial.
For more such questions on polynomial, click on:
https://brainly.com/question/1600696
#SPJ8