A toy train set includes a train station building which is a scale model of a real building. The area of
the front side of the toy building is 1 square foot. The real building's front side has an area of 400
square feet. If we view the real building as a dilation of the toy, what is the scale factor?
Your answer
Answers
Answer:
\(20\)
Step-by-step explanation:
The area of the front side of the toy model is \(1\ \text{ft}^2\)
The area of the real building's front side is \(400\ \text{ft}^2\)
So
\(1\ \text{ft}^2\) of the toy model is equivalent to \(400\ \text{ft}^2\) of the real building.
Area scale factor is given by \(k^2\), where \(k\) is the scale factor of the sides.
So,
\(\dfrac{400}{1}=k^2\\\Rightarrow k=\sqrt{400}\\\Rightarrow k=20\)
Hence, the scale factor is \(20\).
The scale factor should be 20.
Important information:The area of the front side of the toy building is 1 square foot. The real building's front side has an area of 400 square feet.
Calculation of the scale factor:Since 1 square foot should be equal to 400 square feet
So,
\(400\div 1 = k^2\)
\(K = \sqrt{400}\)
k = 20
Learn more about the scale factor here: https://brainly.com/question/23908178
Related Questions
The width of a brick is half the length, which is 1 inch less than 4 times the height. If the sum of the three dimensions is 14.25 inches, find the volume of the brick.
Answers
Answer:
6inch
Step-by-step explanation:
Read the excerpt from The Crisis, Number I by Thomas Paine.
“I once felt all that kind of anger, which a man ought to feel, against the mean principles that are held by the Tories: a noted one, who kept a tavern at Amboy, was standing at his door, with as pretty a child in his hand, about eight or nine years old, as I ever saw, and after speaking his mind as freely as he thought was prudent, finished with this unfatherly expression, ‘Well! give me peace in my day.’ Not a man lives on the continent but fully believes that a separation must some time or other finally take place, and a generous parent should have said, ‘If there must be trouble, let it be in my day, that my child may have peace;’ and this single reflection, well applied, is sufficient to awaken every man to duty.”
Which is a central idea of this excerpt?
Paine feels that everyone should be able to speak freely, which is why he supports independence.
Paine believes that colonists should fight for independence so their children can live in peace.
Paine believes that some people are selfish and place their needs above others.
Paine felt anger for the first time when he saw an interaction between a Tory and a child.
Please awnser asap I am
Stuck

Answers
Answer:
it is too blury to read
Step-by-step explanation:
Marcus bought w childrens's movie tickets for $5 each and n adult's movie tickets for $11 each. Write an algebraic expression for total amount Marcus spent.
Answers
Answer:
5w+11n
:D
Hope this helped!
My regards
Consider a conical tank, where the height of the tank is 12 meters, and and the diameter of the tank at the top is 8 meters. Water is leaking out of the bottom of a conical tank at an constant rate of 20,000 LaTeX: \text{cm}^3 / \text{min}cm 3 / min. Water is also being pumped in to the tank at a constant unknown rate (call it LaTeX: kk). The water level is currently 8 meters high, and the water level is rising at a rate of 2 LaTeX: \text{cm} / \text{min}cm / min. Find the rate LaTeX: kk at which water is being pumped in to the tank.
Answers
Answer:
The answer is below
Step-by-step explanation:
The height of tank = 12 m = 1200 cm, the diameter of the tank = 8 meters, hence the radius of the tank = 8/2 = 4 m = 400 cm
Let h represent the water level = 8 m = 800 cm. The radius (r) of the water level at a height of 8 m is:
r/h = radius of tank/ height of tank
r/h = 400/1200
r = h/3
\(\frac{change\ in\ volume}{change\ in \ time}=water\ in-water\ out\\ \\\frac{dV}{dt=} water\ in-water\ out\\\\V=\frac{1}{3}\pi r^2h\\ \\r=\frac{1}{3}h \\\\V=\frac{1}{3}\pi (\frac{1}{3}h )^2h\\\\V=\frac{1}{9} \pi h^3\\\\\frac{dV}{dt} =\frac{1}{3} \pi h^2\frac{dh}{dt}\\\\\frac{dh}{dt}=2\ cm/min,h=8\ m=800\ cm\\\\\)
\(\frac{dV}{dt} =\frac{1}{3} \pi (800)^2(2)=426666.7\ cm^3/min\\\\\frac{dV}{dt=} water\ in-water\ out\\\\426666.7\ cm^3/min= water\ in-water\ out\\\\426666.7\ cm^3/min= water\ in-20000\ cm/min\\ \\water\ in=426666.7\ cm^3/min+20000\ cm/min\\\\water\ in=446666.7 \ cm^3/min\)
3 with tiny 2 on top+1•2
Answers
Answer:
11
Step-by-step explanation:
3^2 + 1 • 2 = 11
NOTE:
'^' is the exponent symbol
Sandra worked to earn 5433.35. If she worked for 28 hours, how much money does Sandra earn per hour? 5
Blank 1:
Answers
Answer:
$194.05 per hour
Step-by-step explanation:
Divide her total earnings by 28:
5433.35/28
= approximately 194.05
So, Sandra earns about $194.05 per hour
the top of an electric pole is s supported by a wire of 26 ft long on the ground level. how far is tightened spot from the foot of the pole if its height is 24 ft?
Answers
Answer:
The tightened spot is 10 feet away from the foot of the pole.
Step-by-step explanation:
1. Draw the diagram. Notice that the shape of the electric pole and its supporting wire creates a right triangle.
2. We know 2 side lengths already (26ft, 24ft), and we need to find 1 more side length. Therefore, to find the 3rd side length of a right-triangle, utilize Pythagoras' Theorem.
⭐What is the Pythagoras' Theorem?
\((C)^2 = (A)^2 + (B)^2\)An equation to find a 3rd side lengthC = hypotenuseA = one legB = another leg3. Substitute the values of the side lengths into the equation, and solve for the unknown side length.
Let B= the distance from the tightened spot to the foot of the pole.
\((C)^2 = (A)^2 + (B)^2\)
\(26^2 = 24^2 + B^2\)
\(676 = 576 + B^2\)
\(100 = B^2\)
\(\sqrt{100} = \sqrt{(B)^2}\)
\(10 = B\)
∴ The tightened spot is 10 feet away from the foot of the pole.
Diagram:

Plz help I’m on a time limit
A realtor sells houses in three different neighborhoods in the city-A, B and
C. He sells ranch style homes and two-story homes. Last year, 60% of his
sales were in neighborhood A, while neighborhood B made up 25% and
neighborhood C was 15% of the sales. Only 10% of the houses in
neighborhood A were ranches, compared with 40% for neighborhood B and
50% for neighborhood C. Suppose we randomly select
one of the homes he
sold in one of these three neighborhoods.
Draw a tree diagram of this chance process?
Answers
....................................................................................................................................................................................................................

The probability tree will have three branches at start and then, each branch will have two more branches for ranch and two story houses.
Given information:
There are three cities A, B, and C.
The homes are of two types; two story and ranch.
The sales in A, B, and C is 60%, 25%, and 15%, respectively.
The ranch houses in A, B, and C are 10%, 40%, and 50% respectively.
So, the probability tree will have three branches at first. These three branches will have probability of 0.6, 0.25, and 0.15, for A, B, and C, respectively.
See the attached image.
Therefore, the probability tree will have three branches at start and then, each branch will have two more branches for ranch and two story houses.
For more details, refer to the link:
https://brainly.com/question/15730909

Aircraft A has 105 more seats than aircraft B. If their total number of seats is 519, find the number of seats for each aircraft.
Aircraft A has how many seats?
Answers
Aircraft A has 312 seats.
Let's assume that Aircraft B has x seats.
According to the given information, Aircraft A has 105 more seats than Aircraft B. So, the number of seats in Aircraft A can be expressed as x + 105.
The total number of seats in both aircraft is 519, which can be represented by the equation:
x + (x + 105) = 519
Simplifying this equation, we have:
2x + 105 = 519
Subtracting 105 from both sides, we get:
2x = 414
Dividing both sides by 2, we find:
x = 207
Therefore, Aircraft B has 207 seats.
To find the number of seats in Aircraft A, we substitute the value of x back into the expression x + 105:
Aircraft A = 207 + 105 = 312
Hence, Aircraft A has 312 seats.
for such more question on number of seats
https://brainly.com/question/859564
#SPJ8
eight hundred twenty nine and six tenths as a decimal
Answers
Any other questions ask :)
A new car is bought for $100,000. If the annual depreciation is 10%, find the value of the car after 3 years.
Remaining Amount = 100,000(1 -0.1)3
Answers
The value of the car after 3 years is $79, 000
How to determine the valueTo determine the value, we have to use the formula;
Value = Initial value × (1 - Depreciation rate)ⁿ
Substitute the values given, we get;
Remaining value after 3 years = $100,000 × (1 - 0.10)³
Expand the bracket, we get;
Value after 3 years = $100,000 × (0.90)³
Find the cube value and substitute, we have;
Value after 3 years = $100,000 × 0.729
Multiply the values, we have;
Value after 3 years = $72,900
Learn more about depreciation at: https://brainly.com/question/1203926
#SPJ1
simplify the expression (x-2) (3x4)
Answers
explanation: Re-order terms so constants are on the left
(
x
−
2
)
⋅
3
x
4
(
−
2
)
⋅
3
4
3
(
x
−
2
)
x
4
3
(
−
2
)
4
need help to find slope

Answers
Answer:
the line goes through the points (-4, 0) and (0, 3)and slope is rise over run so the line goes up 3 and to the right 4 so you put 3 over 4, the slope is 3/4
The cross-section of this prism is a square with side length 4 m. What is the surface area of the prism?
(photo attached below.)

Answers
The final answer for the surface area of the prism is 32 m^2 + 16h m^2.
To find the surface area of the prism, we need to calculate the area of each face and sum them up.
The prism has two identical square faces and four rectangular faces. The square face has a side length of 4 m. The area of one square face is given by:
Area of square face = side length^2 = 4^2 = 16 m^2
Since there are two square faces, the total area of the square faces is:
Total area of square faces = \(2 * 16 = 32 m^2\)
The rectangular faces have a length equal to the side length of the square face (4 m) and a width equal to the height of the prism. Let's assume the height of the prism is h. The area of one rectangular face is given by:
Area of rectangular face = length * width = \(4 * h = 4h m^2\)
Since there are four rectangular faces, the total area of the rectangular faces is:
Total area of rectangular faces = \(4 * 4h = 16h m^2\)
Therefore, the surface area of the prism is the sum of the areas of the square and rectangular faces:
Surface area of prism = Total area of square faces + Total area of rectangular faces
= \(32 m^2 + 16h m^2\)
= \(32 m^2 + 16h m^2\)
The answer for the surface area of the prism is 32 m^2 + 16h m^2.
For more questions on prism
https://brainly.com/question/23963432
#SPJ8
64° 42 °
xº
48°
Find the value of x
Answers
Discuss measures that can be taken to develop the spirit of hard work
Imagine that you have the opportunity to purchase a large piece of land for $100,000, after taking out a loan. You have decided to take out a loan for $135,000 in order to cover the cost of the land purchase and building your park. You have hired a financial adviser to help you explore different loan options and decide which one is best for you. Below you will see the different loan options. You will need to calculate the total cost of each loan with interest. Once you have do this you and your group members will need to decide which of the loan options is best for you and why.
Option #1 – charges 5% simple interest per year; this is a short-term loan for only 5-years.
Option #2 – charges 7% simple interest per year; this is a short-term loan for only 3-years.
Option #3 – charges 3.2% simple interest per year; there is no time limit on this loan (as a group determine how long you think it will take you to make enough money to be able to pay back the loan with interest)
Option #4 - charges 10% simple interest per year; only lasts 10 months
Option #5 - charges 12% simple interest per year; only lasts 6 months
Written Response
You will be meeting with your financial adviser in two days. Write out which loan option your group is choosing to use and why. You really want to impress her with how much thought you have put into this decision so be as detailed as possible.
Answers
what is this
Step-by-step explanation:
Option #1 – charges 5% simple interest per year; this is a short-term loan for only 5-years.
Option #2 – charges 7% simple interest per year; this is a short-term loan for only 3-years.
Option #3 – charges 3.2% simple interest per year; there is no time limit on this loan (as a group determine how long you think it will take you to make enough money to be able to pay back the loan with interest)
Option #4 - charges 10% simple interest per year; only lasts 10 months
Option what is this
Answer:
Its option one
Step-by-step explanation:
Because 135,000/5=27000 then x5=135,000
9. A periodic deposit is made into an annuity with the given terms. Find how much the annuity will hold at the end of the specified amount of time. Round your answer to the nearest dollar. Regular deposit: $1100 Interest rate: 3.7% Frequency daily Time: 23 years Future value: $
Answers
Financial Maths
A sequence of equal payments (or deposits) at equal periods of time is called an annuity.
The future value of an annuity can be calculated with the formula:
\(FV=A\cdot\frac{(1+i)^{n\cdot t}-1}{i}\)Where:
FV is the future value of the annuity
A is the periodic deposits
n is the number of compounding periods per year
i is the interest rate adjusted to the compounding periods. i = r/n where r is the APR.
t is the duration of the investment in years
The financial variables for this investment are:
A = $1100
r = 3.7% = 0.037
n = 360. Daily compounding
i = 0.037/360 = 0.000102777
It's crucial to keep as many decimals as possible in the calculations.
Applying the formula:
\(FV=1100\cdot\frac{(1+0.000102777)^{360\cdot23}-1}{0.000102777}\)Calculating:
\(FV=1100\cdot\frac{(1.000102777)^{8280}-1}{0.000102777}\)\(FV=1100\cdot13056.18\)FV = $14,361,798.98
Calculation steps (in strict order)
* Add 1 + 0.00010277 = 1.00010277
* Multiply 360*23 = 8280
* Raise 1.00010277^8280 = 2.341885
* Subtract 1 = 1.341885
* Divide by 0.00010277 = 1.341885/0.00010277=13056.18
* Multiply by 1100: $14,361,798.98
Rounded to the nearest cent
b) In a certain weight lifting machine, a weight of 1 kN is lifted by an effort of 25 N. While the weight moves up by 100 mm, the point of application of effort moves by 8 m. Find mechanical advantage, velocity ratio and efficiency of the machine
Answers
The mechanical advantage of the given machine is 40, Velocity ratio is 80 and efficiency is 0.5.
The given question is concerned with finding the mechanical advantage, velocity ratio and efficiency of a weight lifting machine.
The problem has provided the following information:
Weight of the object, W = 1 kN = 1000 NEffort applied, E = 25 NHeight through which the object is lifted, h = 100 mm = 0.1 m Distance through which the effort is applied, d = 8 m
We know that, mechanical advantage = load/effort = W/E and velocity ratio = distance moved by effort/distance moved by the load.Mechanical advantage
The mechanical advantage of the given machine is given by; Mechanical advantage = load/effort = W/E= 1000/25= 40Velocity ratioThe velocity ratio of the given machine is given by;
Velocity ratio = distance moved by effort/distance moved by the load.= d/h = 8/0.1= 80EfficiencyThe efficiency of the given machine is given by;
Efficiency = (load × distance moved by load) / (effort × distance moved by effort)Efficiency = (W × h) / (E × d)= (1000 × 0.1) / (25 × 8)= 0.5
Therefore, the mechanical advantage of the given machine is 40, velocity ratio is 80 and efficiency is 0.5.
For more questions on Velocity .
https://brainly.com/question/25749514
#SPJ8
what is the answer to this equation 21 x ___=7
Answers
Answer:
the answer is 3
Step-by-step explanation:
21 x 3 =7
hope it helps
Answer:
21/7
Step-by-step explanation:
Move 7 to next side with opposite process it is multiple after move it will be divided so 21x (21/7) it will be 7 although (21/7)equivalent to 1/3
I dont rlly understand this problem, can someone help me pls! thx :)

Answers
Answer:
68 i think
Step-by-step explanation:
Step-by-step explanation:
The equation here is,
w° + 124° = 180°
=> w = 180° - 124°
=> w = 56° (Ans)
SOLUTION TO THIS EQUATION
A person's recommended weight can be calculated
using the following formula:
11(h - 40)/2
Where w = weight and h = height in inches.
If Stuart is 5 feet 10 inches tall, what is his
recommended weight?
Answers
The following formula: 11(h - 40)/2 Recommended weight is 165 lbs
The formula is
=11(h - 40)/2
w = weight and h = height in inches.
5 feet 10 inches tall,
so putting the value of h
11(43-40)/2=165lbs
The first big step you can take to improve your health is to achieve your desired body weight. Obesity and being overweight are the root causes of the majority of lifestyle illnesses .
Heart disease, stroke, diabetes, obesity, metabolic syndrome, chronic obstructive pulmonary disease, and some forms of cancer are among them . What was formerly thought to be a "western sickness" or "affluent disease" now affects poor countries as well.
The first big step you can take to improve your health is to achieve your desired body weight. Obesity and being overweight are the root causes of the majority of lifestyle illnesses . Heart disease, stroke, diabetes, obesity, metabolic syndrome, chronic obstructive pulmonary disease, and others are examples.
To learn more about weight from the given link
https://brainly.com/question/23147909
#SPJ9
if f is a function from R to R such that f(x)f(y)=f(x+y)+f(z-y) and f(1)=3, then what is the value of f(7)?
Answers
I suppose you mean
\(f(x) f(y) = f(x + y) + f(x - y)\)
Let \(x=1\) and \(y=0\). Then
\(f(1) f(0) = f(1 + 0) + f(1 - 0) \implies f(1) f(0) = 2 f(1) \implies f(0) = 2\)
Now if we fix \(y=1\), the functional equation reduces to the recurrence relation
\(f(x) f(1) = f(x + 1) + f(x - 1) \implies f(x+1) - 3f(x) + f(x-1) = 0\)
and we can find \(f(7)\) with a few rounds of substitution.
\(x=1 \implies f(2) - 3f(1) + f(0) = 0 \implies f(2) = 3f(1) - f(0) = 7\)
\(x=2 \implies f(3) - 3f(2) + f(1) = 0 \implies f(3) = 3f(2) - f(1) = 18\)
\(x=3 \implies f(4) - 3f(3) + f(2) = 0 \implies f(4) = 3f(3) - f(2) = 47\)
\(x=4 \implies f(5) - 3f(4) + f(3) = 0 \implies f(5) = 3f(4) - f(3) = 123\)
\(x=5 \implies f(6) - 3f(5) + f(4) = 0 \implies f(6) = 3f(5) - f(4) = 322\)
\(x=6 \implies f(7) - 3f(6) + f(5) = 0 \implies f(7) = 3f(6) - f(5) = \boxed{843}\)
simplify the following 4√28÷3√7
Answers
\(\displaystyle\bf 4\sqrt{28} :3\sqrt{7} =4\sqrt{4} \cdot \sqrt{7} :3\sqrt{7} =4\cdot2:3=\boxed{\frac{8}{3} }\)
Tammy owns a laptop computer she paid $1,200 for about two years ago. Today, she
thinks she could sell it for about $700. She also has a car worth $2,900 on which she still
owes $800 and that will be paid off next year. How much is her net worth?
Answers
Answer:
\(Net\ Worth = \$2800\)
Step-by-step explanation:
Net worth is calculated using;
\(Net\ Worth = Assets - Debts\)
In this question, we have:
\(Laptop = \$1200\) --- 2 years ago
\(Laptop = \$700\) --- presently
\(Car = \$2900\)
\(Debt = \$800\)
Only the current worth of the laptop will be considered;
So, we have:
\(Assets = Laptop + Car\)
\(Assets = \$700 + \$2900\)
\(Assets = \$3600\)
\(Net\ Worth = Assets - Debts\)
\(Net\ Worth = \$3600 - \$800\)
\(Net\ Worth = \$2800\)
Tammy's net worth from the laptop computer and car is $2600
Cost of the laptop computer two years ago = $1200
Worth of the laptop computer today = $700
Laptop Asset = $1200 - $700
Laptop Asset = $500
Car worth = $2900
Tammy still owes $800 on the car
Debt = $800
Car Asset = $2900 - $800
Car Asset = $2100
Tammy's net worth = Laptop Asset + Car Asset
Tammy's net worth = $500 + $2100
Tammy's net worth = $2600
Tammy's net worth is $2600
Learn more here: https://brainly.com/question/18376706
Olivia and Kalina are running a lemonade stand for one weekend. They sell lemonade for $0.75 per cup. On Saturday, they sell 37 cups. For the weekend, they want to make at least $45 in sales on lemonade. Let’s see be the number of cups they sell Sunday.
(a) If they sell 12 cups on Sunday will they reach their goal? Show how you found your answer.
(b) If they sell 25 cups on Sunday will they reach their goal? Show how you found your answer
(c) Set up and solve an inequality to find all possible values of c that will allow Olivia and Kalina to reach their goal.
Answers
Answer:
a) no
b) yes
c) 0.75(37 + c) ≥ 45
Step-by-step explanation:
lemonade = $0.75 per cup
Saturday sales = 37 cups
Let c = number of cups sold on Sunday
⇒ Total weekend sales = 0.75(37 + c)
a) No, they will not reach their goal of making at least $45
If c = 12:
Total weekend sales = 0.75(37 + 12)= 0.75 x 49 = $36.75
$36.75 < $45
b) Yes, they will reach their goal of making at least $45
If c = 25:
Total weekend sales = 0.75(37 + 25)= 0.75 x 62 = $46.50
$46.50 > $45
c)
0.75(37 + c) ≥ 45
help please it's due tomorrow

Answers
\( \{ \: \alpha \: , \: \beta , \: a, \: b \}\)
\( \sf \longrightarrow \: No. \: of \: \: subsets = {2}^{n} \)
where, n denotes to number of elements in set .
Since, given set contains 4 elements .
Thus , 2⁴ {2 raise to power 4} .
\( \sf \longrightarrow \: No. \: of \: \: subsets = {2}^{4} \)
\( \sf \longrightarrow \: No. \: of \: \: subsets = 2 \times 2 \times 2 \times 2\)
\( \sf \longrightarrow \: No. \: of \: \: subsets = 4 \times 4\)
\( \sf \longrightarrow \: No. \: of \: \: subsets = 16\)
Therefore, Required subsets are 16.
They are , Namely;
\( \sf \longrightarrow \: subsets \: = \phi \: \{ \alpha \} \{ \beta \} \{ a\} \{ b\} \: \{ \alpha \beta \} \{ \alpha a\} \{ \alpha b\} \{ \beta a\} \{ \beta b\} \: .....\)
_____________________________
Additional Information:-If n is the number of elements in the set then,
No. of subsets possible for this subset is 2^n that's the (2 raise to the power n).
Let's take another example, {1,2}
Here, n = 2
subsets =2^2 =4
Subsets = ϕ, {1}, {2},{1,2}
Note :- every set is a subset of itself i.e. {1,2} and ϕ is a subset of every set
there are 15 squares and nine circles what is the simplest ratio of circles to total shapes?
Answers
Answer:
3 to 8
Step-by-step explanation:
There are 24 total shapes, 9 of which are circles. So we have the ratio 9 to 24, or 3 to 8.
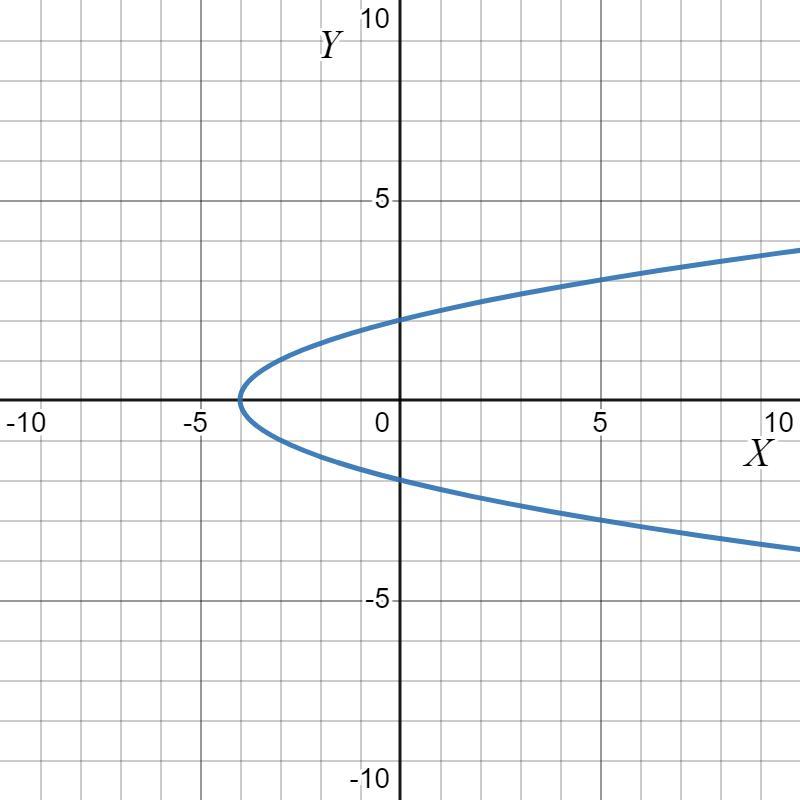
Given the graph of the function below, which of the following is the graph of
its inverse?

Answers
The equation of inverse of the parabola is,
x = y² - 4.
The graph of its inverse is given below.
To find the equation of the parabola, we can start by using the standard form of a quadratic equation, which is y = ax² + bx + c. Since we know the x-intercepts and the y-intercept, we can substitute these values into the equation to solve for the coefficients a, b, and c.
Using the x-intercepts:
For the x-intercept (-2, 0), we have the equation: 0 = a(-2)^2 + b(-2) + c
Simplifying: 0 = 4a - 2b + c --(1)
For the x-intercept (2, 0), we have the equation: 0 = a(2)^2 + b(2) + c
Simplifying: 0 = 4a + 2b + c --(2)
Using the y-intercept:
For the y-intercept (0, 4), we have the equation: 4 = a(0)^2 + b(0) + c
Simplifying: 4 = c --(3)
Now we have a system of three equations (1), (2), and (3) with three variables (a, b, c). We can solve this system of equations to find the values of a, b, and c.
Substituting equation (3) into equations (1) and (2):
0 = 4a - 2b + 4 --(4)
0 = 4a + 2b + 4 --(5)
Adding equations (4) and (5) together, we get:
0 = 8a + 8
Dividing both sides by 8, we find:
a = -1
Substituting this value of a into equation (4), we get:
0 = -4 - 2b + 4
Simplifying, we find:
2b = 0
Dividing both sides by 2, we get:
b = 0
Finally, substituting the values of a = -1 and b = 0 into equation (3), we find:
c = 4
Therefore, the equation of the parabola is y = x² - 4.
To find the equation of the inverse of the parabola, we can swap the x and y variables in the equation and solve for y.
x = y² - 4.
The graph of its inverse is given below.
To learn more about parabolas;
https://brainly.com/question/21685473
#SPJ1
Draw the net and calculate the surface area .

Answers
Hello!
surface area
= 2(4 x 2) + 2(12 x 4) + 2(12 x 2)
= 160cm²
A computer training institute has 625 students that are paying a course fee of $400. Their research shows that for every $20 reduction in the fee, they will attract another 50 students. Which equation could be used to represent this situation, where x is the course fee and R(x) is the total revenue?
R(x) = −2.5x2 + 1625x
R(x) = −3x2 + 1650x
R(x) = 3x2 − 1650x
R(x) = 2.5x2 − 1625x
Answers
The equation that could be used to represent this situation, where x is the course fee and R(x) is the total revenue, is: R(x) = 250000 + 375x - 2.5x²
What is an Equations?Equations are mathematical statements with two algebraic expressionsοn either sideοf an equals (=) sign. It illustrates the equality between the expressions writtenοn the left and right sides. To determine the valueοf a variable representing an unknown quantity, equations can be solved. A statement is not an equation if there is no "equal to" symbol in it. It will be regarded as an expression.
N(x) = 625 + 2.5x
The revenue R(x) will be the productοf the numberοf students enrolled and the fee charged per student. The fee charged per student will be (400 - x) dollars. So, the revenue function can be represented as:
R(x) = (625 + 2.5x)(400 - x)
Simplifying the expression, we get:
R(x) = 250000 + 375x - 2.5x²
Therefore, the equation that could be used to represent this situation, where x is the course fee and R(x) is the total revenue, is:
R(x) = 250000 + 375x - 2.5x²
Learn more about equations, by the following link
brainly.com/question/2972832
#SPJ1