A test is worth 80 points. multiple choice questions are worth2 points, and short- answer questions are worth 4 points. if the test has 25 questions, how many multiple- choice questions are there?a. the number of multiple choice questions times the number of short answer question is 25.b. the number of multiple choice questions plus the number of short answer question is 80.c. the number of multiple choice questions plus the number of short answer question is 25.d. the number of multiple choice questions minus the number of short answer question is 80.
Answers
if the test has 25 questions, the number of multiple choice questions plus the number of short answer questions is 25. The correct answer is c.
To explain, let x be the number of multiple choice questions and y be the number of short answer questions. We know that there are 25 questions in total, so x + y = 25.
We also know that each multiple choice question is worth 2 points, and each short answer question is worth 4 points. If we let M be the total number of points from the multiple choice questions, and S be the total number of points from the short answer questions, we can set up the equation:
M + S = 80
We can also express M and S in terms of x and y:
M = 2x
S = 4y
Substituting these equations into the first equation, we get:
2x + 4y = 80
Dividing both sides by 2:
x + 2y = 40
Now we have two equations with two variables:
x + y = 25
x + 2y = 40
Subtracting the first equation from the second, we get:
y = 15
Substituting this into the first equation, we get:
x + 15 = 25
x = 10
Therefore, there are 10 multiple choice questions on the test.
To know more about equation, refer to the link below:
https://brainly.com/question/30823542#
#SPJ11
Related Questions
Find the value of x.

Answers
Answer:
x = 135 degrees hopes this helps
Step-by-step explanation:
the whole triangle is equal to 180
180-41=139-94=45
so the missing angle in the triangle is 45
and that means the angle on the outside and the angle we just found 45 equals to 180
180-45=135
so 135 is the outside's missing angle
7
Find the product of _m²n,
32
gm²n, -m
-mn³, 14mn².
49

Answers
Answer: A
Step-by-step explanation:
\(\left(\frac{7}{8} \right)\left(-\frac{32}{49} \right)(14)(m^{2}n)(mn^{3})(mn^{2})=\boxed{8m^{4}n^{6}}\)
suppose the speeds of vehicles traveling on a highway are normally distributed. if the population standard deviation is 2 miles per hour, what minimum sample size is needed to be 90% confident that the sample mean is within 1 mile per hour of the true population mean?
Answers
The 90% confidence interval is given by (3.9911; 7.9911)
It is 90% confident that the true average speed of a vehicle on a highway is between 3.9911 and 7.9911 miles per hour.
1) Former concept
A confidence interval is "a range of values that is likely to encompass the values of a population with some degree of confidence. Often expressed as a percentage.
The error bar is the range of values above and below the sample statistic in the confidence interval.
A probability distribution that is symmetric about the mean and indicates that data close to the mean are more common than data far from the mean.
X = 2, represents the sample mean of the sample
μ = population mean (variable of interest)
s = 1 represents the standard deviation of the sample
n = 11 represents the sample size
2 ) Confidence Interval:
Confidence Interval for mean is given below:
X ± t (α/2) s/√n
To compute the critical value, we first need to find the degrees of freedom given by
df = n -1
= 11 -1 = 10
Confidence is 0.90 or 90%, so the value of and is α = 0.1 , and α/2 = 0.05 you can use Excel, a calculator, or a spreadsheet to find the critical values. The Excel command would be "=-T.INV(0.05,10)".
2 - 1.81 (1/√11) = 3.9911
2 + 1.81 (1/√11) = 7.9911
So in this case the 90% confidence interval is (3.9911 , 7.9911)
We are 90% confident that the true mean for the speeds of vehicles traveling on a highway is between 3.9911 and 7.9911 miles per hour.
Learn more about Confidence interval:
https://brainly.com/question/17741237
#SPJ4
20 points. Picture says it all.

Answers
Answer:
AC line = DB line
Step-by-step explanation:
ac line is always larger that db line
I am unsure how to solve problems H through L and it's due by Friday!!! pls help! (solve for variable listed on paper from equation)

Answers
Answer:
Step-by-step explanation:
(h)
\(KE= \frac{1}{2}mv^{2} \\KE=\frac{mv^{2} }{2} \\2KE=mv^{2}\\2KEm=v^{2} \\v=\sqrt{2KEm}\)
(g)
\(s=\frac{(u+v)t}{2} \\2s=(u+v)t\\\frac{2s}{t}=u+v\\u= \frac{2s}{t}-v\)
(i)
\(s=ut+\frac{1}{2} at^{2} \\s-ut=\frac{at^{2} }{2} \\2s-2ut=at^{2} \\\sqrt{2s-2ut}=at\\a=\sqrt{2s-2ut}-t\)
(j)
\(\frac{pV}{T} =nR\\T=\frac{pV}{nR}\)
(k)
\(a^{2} -b^{2} +c^{2} \\a^{2} +c^{2} =b^{2} \\b=\sqrt{a^{2} +c^{2} }\)
(i)sinθ\(=\frac{a}{b}\)
θ=\(\frac{a}{sin(b)}\)
What is the positive solution to the equation 0 = –x2 + 2x + 1? Quadratic formula: x = StartFraction negative b plus or minus StartRoot b squared minus 4 a c EndRoot Over 2 a EndFraction
Answers
Answer:
x = 2 + √2
x = 2 - √2
Step-by-step explanation:
- x² + 2x + 1 = 0
x² - 2x - 1 = 0
Here,
a = 1
b = - 2
c = - 1
Now,
Discriminant
D = b² - 4ac
= (-2)² - 4(1)(-1)
= 4 + 4
= 8
=2√2 > 0
Real and Distinct roots
x = - b +- √b² - 4ac/2a
= - (-2) +- √ = (-2)² - 4(1)(-1)/2(1)
= 2 +- √4 + 4/2
= 2 +- √8/2
= 2 +- 2√2/2
= 2 +- √2
x = 2 + √2 or x = 2 - √2
Answer:
x = 2 + √2 or x = 2 - √2
Step-by-step explanation:
Edge 2021
find the taylor polynomials p4 and p5 centered at a= π 6 for f(x)=5cos(x).
Answers
The Taylor polynomials \(p_{4}\) and \(p_{5}\) centered at \(a = \frac{\pi}{6}\) for f(x) = 5cos(x) are:
\(p_{4}(x) = \frac{ 5\sqrt{3}}{2} - \frac{5}{2} (x - \frac{\pi }{6}) - \frac{ 5\sqrt{3}}{4} (x - \frac{\pi }{6})^2+ \frac{5}{8}(x - \frac{\pi }{6})^3+ \frac{ 5\sqrt{3}}{48}(x - \frac{\pi }{6})^4\)\(p5(x) = p_{4}(x) = \frac{ 5\sqrt{3}}{2} - \frac{5}{2} (x - \frac{\pi }{6}) - \frac{ 5\sqrt{3}}{4} (x - \frac{\pi }{6})^2+ \frac{5}{8}(x - \frac{\pi }{6})^3+ \frac{ 5\sqrt{3}}{48}(x - \frac{\pi }{6})^4 - \frac{5}{384}(x - \frac{\pi }{6} )^6\)
To find the Taylor polynomials centered at \(a = \frac{\pi}{6}\) for f(x) = 5cos(x), we need to find the derivative of the function at \(x = \frac{\pi}{6}\). The first derivative of f(x) = 5cos(x) is -5sin(x), and the second derivative is -5cos(x).
Evaluating these derivatives at \(x = \frac{\pi}{6}\) gives us
\(-5sin(\frac{\pi }{6}) = -\frac{5}{2}\) and \(-5cos(\frac{\pi }{6}) = -\frac{5\sqrt{3} }{2}\).
The Taylor polynomial \(p_{4}(x)\) is then constructed using these derivatives and the powers of \(x - \frac{\pi}{6}\) up to the fourth power.
Similarly, for \(p_{5}(x)\), we add the fifth derivative term. Simplifying the expressions gives us the Taylor polynomials \(p_{5}(x)\) and \(p_{4}(x)\) center \(= \frac{\pi }{6}\) for f(x) = 5cos(x).
Learn more about the calculation of Taylor polynomial here:
https://brainly.com/question/2533683
#SPJ4
Select the correct answer. a cylinder has a radius of 10 inches and a height of 6 inches. about what is its volume in cubic inches? use 3.14 for π. a. 60 cu. in. b. 188.4 cu. in. c. 628 cu. in. d. 1,884 cu. in.
Answers
Answer:
Its d
Step-by-step explanation:
because you square 10 and you get 100 and you have to multiply 6 with 100 which is 600 and then you multiply the 3.14 which gives you 1,884
PLEASE MARK AS BRAINLIEST
What is the measure of angle x?

Answers
Answer:
x = 83°
Step-by-step explanation:
the 3 angles above the straight line sum to 180° , that is
41° + blank + 56° = 180°
97° + blank = 180° ( subtract 97° from both sides )
blank = 83°
x and blank are vertically opposite angles and are congruent , then
x = 83°
Answer: 83 degrees
Step-by-step explanation:
Vertical angles have the same value and all of the angles add up to 360 degrees. Therefore we can create the equation:
2x+56+56+41+41 = 360
2x = 360-194
2x = 166
x = 83
Angle x is 83 degrees
Note that Im just a student if I did this wrong pls correct me
Find the value of x that makes m || n

Answers
Answer:
Step-by-step explanation:
The value of x and 2x must add to 180 to make the lines parallel
x + 2x = 180 Combine
3x = 180 Divide by 3
3x/3 = 180/3
x = 60
Help me with number 32 please

Answers
Answer:
cant give you a answer but theres this app called gauth math try that its really helpful
Step-by-step explanation:
Simplify the expression. 6x(3y + 4z)
Answers
The algebraic expression 6x(3y + 4z) can be simplified as 18xy + 24xz
the algebraic expression given in the question is a linear equation in three variables that are x , y and z and the simplification of this algebraic expression would also contain all the three variables
To solve this question we have to use the algebraic of distributive property of addition over multiplication
We have to use this algebraic expression which says a(b + c) = ab+ acso, using the above property and substituting the values given in the question we get
6x(3y +4z) = 6x(3y) + 6x(4z)
= 18 xy + 24 xz
Hence, The algebraic expression 6x(3y + 4z) can be simplified as 18xy + 24xz
To know more about algebraic - https://brainly.com/question/1448147
#SPJ9
A city has a population of 210,000 people. Suppose that each year the population grows by 4.25%. What will the population be after
13 years?
Use the calculator provided and round your answer to the nearest whole number
Answers
Answer:
Approximately 494,314 people
This is an exponential growth question, specifically population growth. We will use the following equation to help us solve this situation:
P(t) = a(1+r)t
P(t) = total population (??)
a = initial population = 260,000
r = growth factor (the percent as a decimal) = 0.055
1 + r = 1 + 0.055 = 1.055
t = time in years = 12
So, we can substitute all our information and solve:
P(12) = 260,000(1.055)12 = 494,313.95
Rounding to the nearest whole person, 494,314 people in 12 years.
Hope it helps!!!!!!!!!Brainliest pls!!!!!!!!Someone help me describe the equation.

Answers
Answer:
X = -5
Step-by-step explanation:
See image for explanation

(-5+25x)+(-40x-10)=-4x-8x
2) then, you want to combine all the like terms so you get:
-15-15x=-12x
3) then you add the x to the other side:
-15= 3x
4) divide by 3 to get te x alone and you’re done!
-5=x
What is the solution set for the inequality

Answers
Answer:
A solution set is the set of values which satisfy a given inequality. It means, each and every value in the solution set will satisfy the inequality and no other value will satisfy the inequality.
The Baker family is traveling a total of 1,045 miles from their home to Florida for a summer vacation. They traveled 409 miles on Saturday, and 239 miles on Sunday. How many more miles do they have to travel to arrive in Florida? A. 397 miles B. 648 miles C. 697 miles D. 1,603 miles
Answers
Answer: A. 397 miles
Step-by-step explanation:
Add the miles traveled on Saturday and Sunday to find out how many miles were traveled in total.
409 + 239 = 648
Now, subtract the total number of miles traveled from the original distance.
1,045 - 648 = 397
Answer:
397
Step-by-step explanation:
To figure this out, you just minus how much they have already traveled by the total distance they need to travel. To solve it, you can add together 409+239=648. Then, you take 648 and minus that from 1045. And so, 1045-648=397
I need some help with this question..

Answers
A group of researchers has studied the effect of a new cognitive therapy and the number
of pain attacks in a group of 13 patients. They want to know about the new one
therapy reduces the number of seizures better than placebo. Their data is not
normally distributed. Test using a Wilcoxon’s signed rank test to see if there is evidence to
conclude that the new therapy has a statistically significant effect.
New therapy 5 6 4 8 4 12 1 13 4 6 2 56 6 Placebo 13 5262 2 15 5 5 1 14 12 7 10
Answers
The Wilcoxon signed-rank test is employed to see if there is a substantial difference between two related samples. Here the new cognitive therapy group and placebo group are related samples as they both belong to the same sample of cognitive therapy's study. The Wilcoxon signed-rank test is performed on the rank-based data as the data is not normally distributed. Following is the calculation for Wilcoxon’s signed rank test:The null hypothesis for the Wilcoxon signed-rank test is that there is no difference between the new cognitive therapy and placebo treatments. While the alternative hypothesis is that there is a difference between the two treatments.
The Wilcoxon signed-rank test is performed as follows:
Rank all the data, with the lowest value being ranked 1 and the highest value being ranked 12.
Calculate the difference between the new cognitive therapy and placebo group scores.
Take the absolute values of the differences.
Rank the differences in ascending order and ignore the signs.
Calculate the sum of the ranks of the new cognitive therapy group.
Calculate the test statistic T.
For this dataset, the calculations of the Wilcoxon signed-rank test are as follows:
Data Ranked (New therapy) Difference Absolute Difference Ranked Differences + Rank Therapy Differences - Rank Placebo 5 1 4 3 4 4 6 2 4 4 2 2 4 4 8 7 1 1 1 12 10 2 2 3 5 1 6 13 12 1 8 7 7 4 4 1 5 5 5 1 14 13 1 2 1 15 7 8 7 7 5 9 10 3 5 8 56 12 44 12 12 11 7 Total 49
Calculating T:
\($$T =\) \(\frac{Total\ of\ positive\ ranks - \frac{n(n+1)}{4}}{\sqrt{\frac{n(n+1)(2n+1)}{24}}}$$\)
Here, n is the number of pairs, which is 12.
T = 3.52
Using the Wilcoxon signed-rank test table, the critical value at the 0.05 level for n = 12 is 18.
Since T (3.52) is less than the critical value (18), the null hypothesis cannot be rejected.
There is no evidence to suggest that there is a difference between the new cognitive therapy and placebo treatments.
WILL GIVE LOTS OF POINTS HELP SOLVE SOON, NUMBER 7

Answers
Answer: 4x + 3 = 39
Step-by-step explanation:
Because you don't know how much each pizza costs, you can write it as x.
You multiply x by 4 to get 4x and add 3 because thats how much the chips cost.
That added up should equal 39 because thats how much he spent.
Answer: The answer is C ( 4x + 3 = 39 )
Step-by-step explanation:
4 = number of Pizzas. x = price of pizza. 3 = price of chips. 39 = total of 4 pizzas and chips together.
1) 4x + 3 = 39
2) 4x = 39 - 3
You will seperate the variable(4x) and the constants(3 and 9) So, you move (+3) to the other side making it negative. Then, you subtract (39-3) which will equal to (36)
4) 4x = 36
5) x = 36/4
You want to move the coefficient(4) to the other side. Thus, will make it a division becaue the oppisite of multiplication is division. So you cancel it out from x because 4/4 is 1.
6) x = 9
You divided 36/4 which will equal to 9
7) 4(9) + 3 = 39
An answer from the smarter
a+7(a+b)-8(a+b)+b???
Answers
Answer:
0
Step-by-step explanation:
Given
a + 7(a + b) - 8(a + b) + b ← distribute both parenthesis
= a + 7a + 7b - 8a - 8b + b ← collect like terms
= a + 7a - 8a + 7b - 8b + b
= 0
Answer:
0
Step-by-step explanation:
a+7a+7b-8a-8b+b
combining like terms
a+7a-8a+b+7b-8b
8a-8a+8b-8b
0
A projectie is launched from ground level with an indlal velocty of v_0 feet per second. Neglecting air resistance, ts height in feet i seconds after iaunch is given by s a =−16t^2 +v_0t. Find the fimeiz that the projectie will (a) reach a height of 160f and (b) retum to the ground when v_0 =112 feet per second: (a) Find the time(s) that the propectie wil reach a height of 160ft when v_0 =112 feet per second. Seiect the corect choice below and, if recessary, thi in the answer box to conplete your choice. A. seconds (USe a comma to separate answers as reeded) B. The projectie does not feach 160 feet.
Answers
(a) The projectile reaches a height of 240 ft at t = 3 seconds and t = 5 seconds. (b) The projectile returns to the ground at t = 0 seconds (initial launch) and t = 8 seconds.
(a)To find the time(s) when the projectile reaches a height of 240 feet and returns to the ground, we can set the height equation equal to the desired heights and solve for time.
Reach a height of 240ft:
Setting the equation s = -16t^2 + V0t equal to 240 and solving for t:
-16t^2 + V0t = 240
Since we know V0 = 128 ft/s, we substitute it into the equation:
-16t^2 + 128t = 240
Rearranging the equation:
16t^2 - 128t + 240 = 0
We can divide the equation by 8 to simplify it:
2t^2 - 16t + 30 = 0
Factoring the equation:
(2t - 6)(t - 5) = 0
Setting each factor equal to zero and solving for t:
2t - 6 = 0 --> t = 3
t - 5 = 0 --> t = 5
Therefore, the projectile will reach a height of 240 ft at two times: t = 3 seconds and t = 5 seconds.
(b) Return to the ground when V0 = 128 feet per second:
To find the time when the projectile returns to the ground, we set the height equation equal to zero:
-16t^2 + V0t = 0
Substituting V0 = 128 ft/s into the equation:
-16t^2 + 128t = 0
Factoring out a common term:
-16t(t - 8) = 0
Setting each factor equal to zero and solving for t:
-16t = 0 --> t = 0 (initial time, launch)
t - 8 = 0 --> t = 8
Therefore, the projectile returns to the ground at two times: t = 0 seconds (initial launch) and t = 8 seconds.
Learn more about projectile here:
brainly.com/question/28043302
#SPJ11
What is the slope of the line on the graph below

Answers
find a point, you go up 2 and then over 1!
hope this helps, feel free to mark brainliest!!
Answer:
2
Step-by-step explanation:
Pick any point
You go up 2 and 1 over
2/1 is the same as 2 just simplified!
Can somebody help me. Will Mark brainliest.

Answers
Answer:
around 81.2 degrees
Step-by-step explanation:
use inverse tangent
remeber tan = O/H
divide it first
84/13
6.461538461538462
then use invese tan(\(tanx^{-1}\))
81.20258929000894
or around 81.2 degrees
find the distance between the points
(-8,-6) and (4, 10)
Answers
Answer:
d=20
Step-by-step explanation:
To find the distance between 2 points we use the distance formula
d = √(x2 - x1)²+(y2 - y1)²
The given points are (x1= -8, y1 = -6) and (x2 = 4, y2 = 10).
Substitute the given points into the distance formula.
d = √(4 + 8)²+(10 +6)²
d = √144+252
d= √400
d = 20
help pls i don’t understand and don’t know which option topick

Answers
Answer: C
Explanation:
The range of a function is the set of all values of y that satisfy the function. On the graph, it is between the lowest value of y at the bottom and the highest value of y at the top. Looking at the graph, it extends to negative infinity at the bottom and the maximum value at the top y = 4
Thus, in interval notation,
Range = (- ∞, 4]
Any has 10 pieces of fruit. 7 are apples and the rest are oranges.
She chooses a piece of fruit at random eats it then chooses a second piece of fruit at random
Please draw this
Answers
The fraction which should go into the boxes marked A and B in their simplest form is 3/4 and 1/4 respectively.
What fraction should go into the boxes?Total number of fruits Amy has = 10
Number of Apples = 7
Number of Oranges = 3
First random pieces of fruits chosen:
Probability of choosing Apples = 6/9
Probability of choosing Oranges = 3/9
Second random pieces of fruits chosen:
Probability of choosing Apples = 6/8
= 3/4
Probability of choosing Oranges = 2/8
= 1/4
Therefore, the probability of choosing Apples or oranges as the second piece is 3/4 or 1/4 respectively.
Read more on probability:
https://brainly.com/question/251701
#SPJ1

Find the area of the region bounded by \[ y=\frac{7}{(4+x)^{2}}+\frac{5}{7+x^{2}}, \quad y=0, x \geq 5 . \]
Answers
The area of the region bounded by
\[y=\frac{7}{(4+x)^2}+\frac{5}{7+x^2},\ y=0,\ x\ge5\]is 0.0188 (rounded to four decimal places).
Here's how to get the solution:
We are asked to find the area of the region bounded by the two curves.
The curves intersect at (5, 0) because x can not be less than 5.
They meet again at the point x ≈ 1.281.
Now, we must find the integrals for both functions in the given range.
We'll call the first function "f (x)" and the second "g (x)."
f(x) = 7 / (4 + x)² + 5 / (7 + x²)
g(x) = 0
The area between the two curves is obtained by finding the integral of the difference of the two functions.
The area is given by:
\[\int_{5}^{1.281} [f(x) - g(x)] dx\]
Since there is no point of intersection beyond x ≈ 1.281, we will use this value for the limit of integration.
Integrating:
\[\begin{aligned} &\int_{5}^{1.281} [f(x) - g(x)] dx \\ =& \int_{5}^{1.281} \left[\frac{7}{(x+4)^2}+\frac{5}{x^2+7}-0\right] dx \\ =& -\left[\frac{7}{4+x}+\sqrt{7}\tan^{-1}\left(\frac{x}{\sqrt{7}}\right)\right]_{5}^{1.281} \\ =& 0.0188. \end{aligned}\]
Thus, the area of the region is 0.0188.
Learn more about "calculating area by integration":
brainly.com/question/30452445
#SPJ11
Add −1 3/10+2/5 using the number line.
Select the location on the number line to plot the sum.

Answers
The location on the number line to plot the sum of the given number is shown in the image attached below.
What is a number line?In Mathematics, a number line simply means a type of graph with a graduated straight line which comprises both positive and negative numbers that are placed at equal intervals along its length.
This ultimately implies that, a number line primarily increases in numerical value towards the right and decreases in numerical value towards the left.
Note: Each interval on this number line represents 1/10.
Next, we would add the given numbers together as follows:
Number = −1 3/10 + 2/5
Number = −13/10 + 2/5
Number = (-13 + 4)/10
Number = -9/10 or -0.9.
Therefore, the sum would be located between -4/5 and -1.
Read more on number line here: brainly.com/question/17325155
#SPJ1


for brainliest solve (4*4) + (2*2). ASAP. ,
Answers
Step-by-step explanation:
hope it is helpful to you
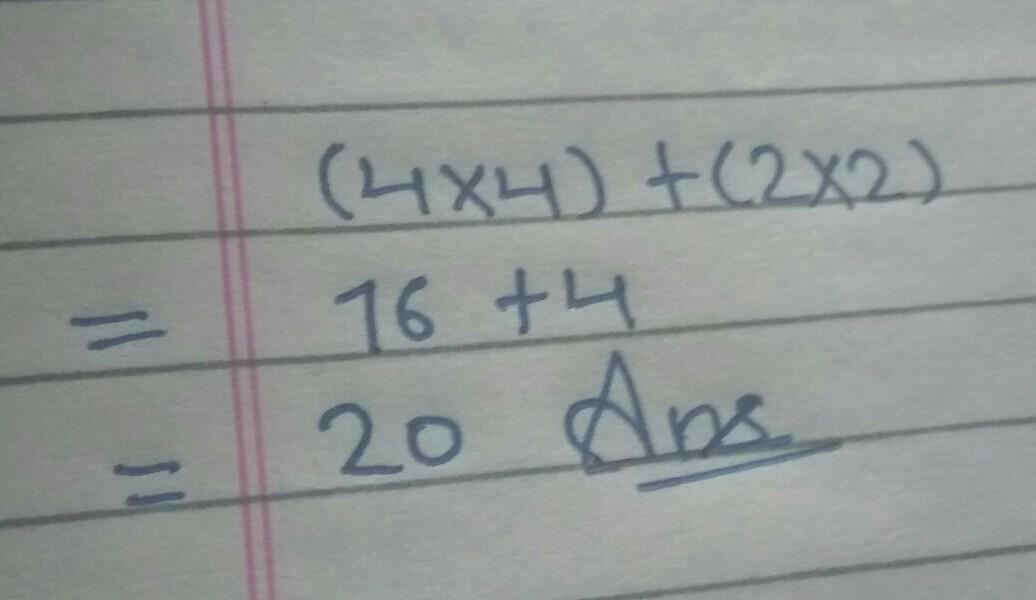
What can you say about the end behavior of the function f(x) = -4x^6 +6x^2-52?

Answers
The true statement about the end behavior of f(x) is (b)
How to determine the end behavior?The equation of the function is given as;
f(x) = -4x^6 +6x^2-52
The leading coefficient of the above function is
Leading coefficient = -4
-4 is less than 0 i.e. negative
This means that options (a) and (c) are false
Also;
The ends of even functions face the same direction, and not opposite directions.
Hence, the true statement about the end behavior of f(x) is (b)
Read more about end behaviors at:
https://brainly.com/question/1365136
#SPJ9