A system of linear equations is shown below.
{2m+4p=22
{6m+12p=66
Complete the statement by selecting the correct phrase from the provided list.
The system of linear equations has _________________________.
A unique solution
no solution
inf many solutions
Answers
Answer: No solution
Step-by-step explanation:
2m+4p=22
6m+12p=66
First, to choose one variable to simplified, I choose to find 1st equations in m form.
2m+4p=22
2m=22-4p [Subtract 4p from both side]
m=22/2 - 4/2p [Divide 2 on both side to find m]
m= 11 - 2p
6m+12p=66
6(11-2p)+12p=66 [Plug in the 11-2p in to m,according to the 1st equation]
66-12p+12p=66
The -12p has cancel with 12p, so it means that there is no solution
Related Questions
a fair die of 20 sides (d20) is rolled. what is the probability that the outcome is either odd or a multiple of 6?
Answers
The probability of rolling an odd number or a multiple of 6 on a d20 is 0.6 (10/20 + 4/20 - 2/20). This can also be expressed as a probability of 60%.
The probability of rolling an odd number or a multiple of 6 on a d20 is calculated using the following formula:
P(odd or multiple of 6) = P(odd) + P(multiple of 6) - P(odd and multiple of 6)
P(odd) = 10/20 or 0.5
P(multiple of 6) = 4/20 or 0.2
P(odd and multiple of 6) = 2/20 or 0.1
Therefore, the probability of rolling an odd number or a multiple of 6 on a d20 is 0.6 (10/20 + 4/20 - 2/20). This can also be expressed as a probability of 60%.
Learn more about probability here:
https://brainly.com/question/30034780
#SPJ4
Find the coordinate of the missing vertex of rectangle ABCD with A(-5,4), B(3,4), and D(-5,-3).
Answers
Answer:
(3 , -3)
Step-by-step explanation:
The missing vertex of rectangle ABCD is C(3, -3).
What are the coordinates?Coordinates are a collection of numbers that aid in displaying a point's precise location on the coordinate plane.
Given:
ABCD is a rectangle.
And the vertices are A(-5,4), B(3,4), and D(-5,-3).
We know,
the parallel sides of a rectangle are equal.
Plotting coordinates of all the vertex.
We get,
the missing vertex is C(3, -3)
To verify that segments are equal or not:
Now, AB = √{(-5 - 3)² + (4 - 4)²} = √{64} = 8 units
CD = √{(-5 - 3)² + (-3 + 3)²} = √{64} = 8 units.
Therefore, the missing vertex is C(3, -3).
To learn more about the coordinates;
https://brainly.com/question/27749090
#SPJ2

A student's work to solve an equation is shown.

Answers
9514 1404 393
Answer:
incorrectlyone solutionStep-by-step explanation:
The third line of the solution is incorrect. It should be ...
5x +2 = -5x +2
Then the one solution can be found:
10x = 0 . . . . . . . . . add 5x-2 to both sides
x = 0
Write the event as set of outcomes. when we roll two dice, the total showing is eight.
Answers
3 5
5 3
4 4
2 6
6 2
Hope this helps, would appreciate brainliest
HELP ITS MATH AND I SUCK AT MATH WILL GIVE BRAINLIEST :)))))

Answers
Answer:
i believe it's A. f(x) slope is greater than g(x) slope
Step-by-step explanation:
the slope of f(x) is -2, while g(x) is -6. you may think "why isn't -6? 6 is bigger, isn't it?" In this case, they're both negative so the number closer to zero is the greater one
Answer:
A
Step-by-step explanation:
PLZ HELP ASAP WILL MARK BRAINLIEST

Answers
Answer:
A value is 6.
Step-by-step explanation:
Help me find the answer

Answers
Answer:
1, 2, 4, 5, 10, 20
Step-by-step explanation:
factors of 20
Answer:
Morris can have 20, 10, 5, 4, and 2
If i've missed any, let me know.
Step-by-step explanation:
Use the information to find and compare Δy and dy. (Round your answers to three decimal places. )
y = 0. 8x5 x = 1 Δx = dx = 0. 1
Δy = dy =
Answers
The computation shows that the values of Δy and dy will be 0.572 and 0.4 respectively.
How to compute the values?The value of Δy will be computed thus:
Δy = y(x + Δx) - y(x)
= y(1.1) - y(1)
= 0.5(1.1)⁸ - 0.5(1)⁸
= 0.572
The value of dy will be:
= y'(x)dx
= (0.5)⁸ × x⁷(0.1)
= 0.4 (1)⁷
= 0.4
Learn more about finding values on:
https://brainly.com/question/25927269
2. Simplify the expression (5-3i) (-7 - 31) - (6-2i). Show your work

Answers
Answer:
\( - 50 + 8i\)
Step-by-step explanation:
\(1. \: - 35 - 15i + 21i - 9 - (6 - 2i) \\ 2. \: - 35 - 15i + 21i - 9 - 6 + 2i \\ 3. \: ( - 35 - 9 - 6) + ( - 15i + 21i + 2i) \\ 4. \: - 50 + 8i\)
which function is nonlinear ?y=4x^3 , y=4x+3 , y=-4/3x
Answers
Answer:
y=4x³ is not linear
Step-by-step explanation:
All of the equations produce lines, one of the characteristics of a linear function, except for y=4x³ where the graph is a curve. Refer to the graph attached to see this.

Proteins can transport other substances to wherever they are needed in the body.
TRUE
FALSE
Answers
Answer:
proteints hi where they need to go body
what trinomial is represented by the tiles in the square?
Answers
Answer:
X^2-12x+ C
Step-by-step explanation:
Move 12x
To find the value c=(b/2^2,divide the coefficient of X by 2 and square the result.
Divide 12 by 2
(-1.6)^2
Multiply-1 by 6
(-6)^2
Raise -6 to the power of 2
36
the proportion of college football players who have had at least one concussion is estimated to be 34% in the united states. we wanted to know if football players at our university were less likely to have suffered a concussion, so we surveyed a random sample of 100 past and present football players at our university. is this survey valid or not valid for testing the hypothesis that the proportion of college football players at our university with at least one concussion is less than the national average?
Answers
All of the criteria's are fulfilled the survey is valid.
We have the information from the question:
The proportion of college football players who have had at least one concussion is estimated to be 34% in the united states.
Then, 34% = 0.34
The sample size of the data is = 100
p: the ‘proportion’ of ‘college’
The required conditions for testing the hypothesis of population proportion are,
(i) The population is larger than the sample
(ii) np > 10
=> 100 × 0.34
=34
(iii) n(1-p) > 10
100 × (1 - 0.34)
=> 100 × 0.66
=66
iv)The ‘sample’ is drawn randomly from the population.
Since all of the above criteria's are fulfilled the survey is valid.
Learn more about Sample size at:
https://brainly.com/question/30885988
#SPJ4
I need help with these questions! My teacher didn’t teach me how to do these-
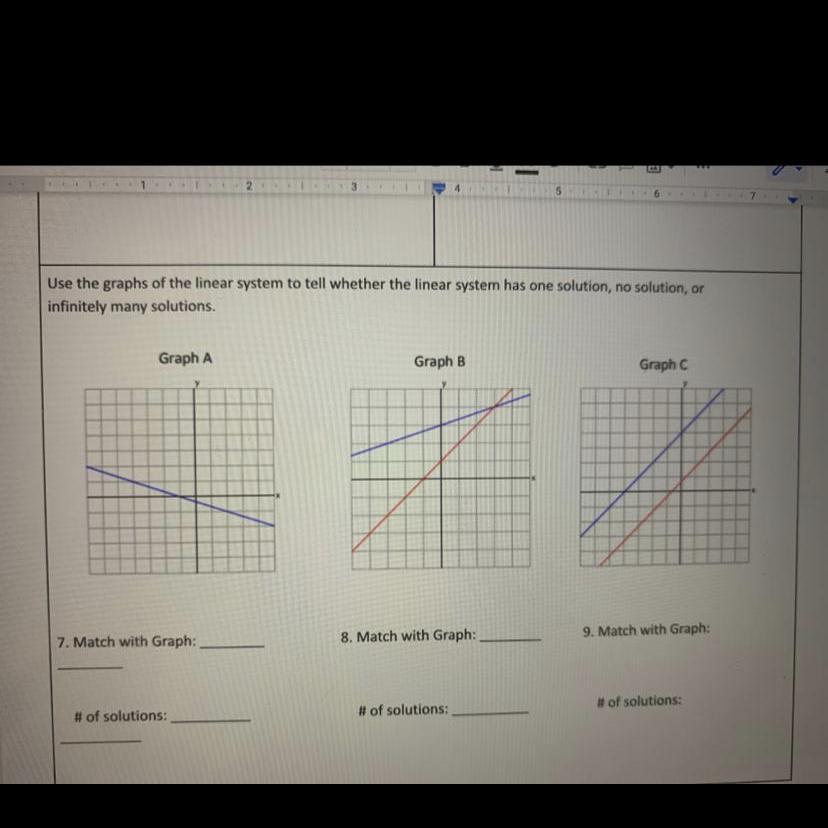
Answers
Answer:
Graph A has infinite solutions, Graph B has one solution, and Graph C has no solutions
Step-by-step explanation:
on a scatter plot, the line that runs through the center of the dots is called a ______________.
Answers
On a scatter plot, the line that runs through the center of the dots is called a "trendline" or "line of best fit."
Scatter Plot: A scatter plot is a graphical representation of data points in a Cartesian coordinate system, where each point represents the values of two variables.
Data Points: Each data point on the scatter plot represents the values of the two variables being plotted. The position of each point is determined by the respective values of the variables.
Trendline: A trendline is a line that attempts to represent the general pattern or trend in the data. It is often drawn through the center of the dots to provide a visual indication of the relationship between the variables.
Line of Best Fit: The trendline is also known as the "line of best fit" because it is the line that minimizes the overall distance between the line and the data points. It represents the best approximation of the overall trend in the data.
Therefore, the trendline or line of best fit on a scatter plot is the line that runs through the center of the dots and represents the general pattern or trend in the data.
To know more about trendline, visit:
https://brainly.com/question/16655332
#SPJ11
Samwell bought a packet of pens. His receipt is shown above. Assume that sales tax is rounded to the nearest cent. If the 6% sales tax had been computed on the sale price instead of on the regular price, how much lower would the tax have been?
Answers
If the 6% sales tax had been computed on the sale price instead of on the regular price, the tax will be $0.04 lower.
How to calculate the difference?It should be noted that from the information, Samwell bought a packet of pens and his receipt is shown above as $2.04.
Assume that sales tax is rounded to the nearest cent, If the 6% sales tax had been computed on the sale price instead of on the regular price, the difference will be:
Sales price = $1.89
Tax = $1.89 × 0.06 = $0.11
Therefore, the difference will be:
= Former tax amount - New tac amount
= $0.15 - 0.11
= $0.04
Learn more about tax on:
brainly.com/question/25783927
#SPJ1

several asset-based 3pls have considerable investments in facilities. the 3pl identified as having the most distribution (warehousing) space in square feet is:
Answers
Determining the 3PL with the most distribution space requires specific data on the size and capacity of each company's facilities.
The 3PL identified as having the most distribution (warehousing) space in square feet cannot be determined without specific information or data.
There are many asset-based 3PLs in the logistics industry, and their distribution space can vary significantly based on factors such as company size, industry focus, geographic coverage, and investments in facilities.
Without specific data on the distribution space of each asset-based 3PL, it is not possible to determine which one has the most square footage.
Asset-based 3PLs are companies that own and operate their own assets, such as warehouses, trucks, and equipment, to provide logistics and supply chain services.
These companies often make significant investments in their facilities to ensure efficient storage and distribution of goods for their clients.
Some large 3PL providers may have extensive warehousing networks and substantial distribution space, while smaller or specialized providers may have more focused or limited warehouse capacities.
Therefore, determining the 3PL with the most distribution space requires specific data on the size and capacity of each company's facilities.
To know more factors click here
brainly.com/question/29128446
#SPJ11
The price of an item yesterday was $60. Today, the price fell to $42. Find the percentage decrease.
Answers
Answer:
-30% or 30% decrease
Step-by-step explanation:
What's percentage decrease?
Percent decrease is the difference between the initial value and new value, indicating a loss of value. The formula to find percent decrease is \(\frac{NV-IV}{IV} * 100\), where NV = new value and IV = initial value.How do we solve this problem?
We know that the original value was $60, so that represents IV. Also, now that the price is $42, it represents NV. Now, we plug in the values!\(\frac{42-60}{60} * 100\) \(\frac{-18}{60} * 100\) \(-\frac{3}{10} * 100\) \(-3 * 10\) \(-30\)Therefore, the answer is 30% decrease.
Put these numbers in order from least to greatest.
0.92,0.43, and 9/10
Answers
Answer:
0.43,9/10,0.92
Step-by-step explanation:
Answer:
0.43, 9/10, 0.92
Step-by-step explanation:
9/10=0.9=0.90
Then after you graph what is the ordered pair (x,y)

Answers

Answer:
Step-by-step explanation:

Consider a monopolist selling a product with inverse demand of PD=12−Q. The firm currently has production costs of C(q)=5+6Q. The firm has the option of attempting to develop a new technology that would lower production costs to C(q)=5+2Q. Research and development costs are $4 if undertaken and must be incurred regardless of whether or not the new technology is "successful" or a "failure." This means that in case of failure, the firm still needs to produce with C(q)=5+6Q but incurs $4 in sunk costs. If the firm attempts to develop the new technology, the innovation will be successful with probability p=3/8. Throughout your analysis, restrict attention to the profit/loss of the firm in only the current period (i.e., assume that the firm will not be operating in any future period).
1. Assume that the monopolist is risk averse, what would be the expected utility of perfect information [assuming that U(Payoff)=sqrt(Payoff)]?
2.75
3.0
3.25
3.5
2. Assume that the monopolist is risk averse, what would be the maximum willingness to pay for perfect information?
3.0
3.25
3.56
4.0
3. Assume the monopolist could consult an engineer who, while not being able to provide perfect information, can evaluate the new technology as either "Promising" or "Risky." You then update your preferences. If P(Success)×P(Promising|Success) = 0.3, what is then the updated probability of P(Risky | Success)?
1/10
2/10
3/10
4/10
4. Assume the monopolist could consult an engineer who, while not being able to provide perfect information, can evaluate the new technology as either "Promising" or "Risky." You then update your preferences. If P(Failure)×P(Risky|Failure) = 0.5, what is then the updated probability of P(Promising| Failure)?
1/10
2/10
3/10
4/10
5. After updating preferences, what is the monopolist's probability of obtaining a promising result, P(Promising) =
17/40
18/40
19/40
20/40
6. After updating probabilities, what is the monopolist's probability of obtaining a risky result, P(Risky) =
21/40
22/40
23/40
24/40
7. Assume the monopolist is told by the engineer that the technology is "promising," what's the monopolist's expected payoff from pursuing the new technology?
11.29
12.19
21.91
29.11
8. Assume the monopolist is told by the engineer that the technology is "risky," what's the monopolist's expected payoff when pursuing the new technology?
0.29
0.92
2.09
20.9
9. After updating probabilities, what is the monopolist's expected payoff from the engineer's information?
5.3
6.2
7.1
8.0
10. Assuming risk-neutrality, what is the monopolist's maximum willingness to pay for the engineer's evaluation?
1.3
2.2
3.1
4.0
11. Assuming risk-aversion [U=sqrt(Payoff)], what is the monopolist's maximum willingness to pay for the engineer's evaluation?
0.65
1.65
2.65
3.0
Answers
Answer:
The expected utility of perfect information is the maximum expected utility with perfect information minus the expected utility without perfect information.
With perfect information, the firm would know whether the new technology is successful or not, so the expected profit would be:
Probability of success * (Revenue - Cost with new technology) + Probability of failure * (Revenue - Cost without new technology)
= 3/8 * (12 - Q - 5 - 2Q) + 5/8 * (12 - Q - 5 - 6Q)
= 13/4 - Q/2
The maximum expected utility with perfect information is the square root of the expected profit, which is sqrt(13/4 - Q/2).
Without perfect information, the firm faces two possible outcomes: success with probability 3/8 and failure with probability 5/8. The expected profit is the probability-weighted average of the profits in each case:
Expected profit = Probability of success * Expected profit with success + Probability of failure * Expected profit with failure
The expected profit with success is (12 - Q - 5 - 2Q) = 7 - 3Q, and the expected profit with failure is (12 - Q - 5 - 6Q) = 7 - 7Q. Therefore:
Expected profit = 3/8 * (7 - 3Q) + 5/8 * (7 - 7Q)
= 27/8 - 5Q/8
The expected utility without perfect information is the square root of the expected profit, which is sqrt(27/8 - 5Q/8).
Thus, the expected utility of perfect information is:
sqrt(13/4 - Q/2) - sqrt(27/8 - 5Q/8) = 3.25
Therefore, the answer is option C, 3.25.
The maximum willingness to pay for perfect information is equal to the difference between the expected profit with perfect information and the expected profit without perfect information.
The expected profit with perfect information is:
Probability of success * (Revenue - Cost with new technology) + Probability of failure * (Revenue - Cost without new technology)
= 3/8 * (12 - Q - 5 - 2Q) + 5/8 * (12 - Q - 5 - 6Q)
= 13/4 - Q/2
The expected profit without perfect information is:
Expected profit = Probability of success * Expected profit with success + Probability of failure * Expected profit with failure
The expected profit with success is (12 - Q - 5 - 2Q) = 7 - 3Q, and the expected profit with failure is (12 - Q - 5 - 6Q) = 7 - 7Q. Therefore:
Expected profit = 3/8 * (7 - 3Q) + 5/8 * (7 - 7Q)
= 27/8 - 5Q/8
The maximum willingness to pay for perfect information is:
13/4 - Q/2 - (27/8 - 5Q/8) = 3.25 - 3Q/8
Therefore, the answer is option B, 3.25.
i need help on number 5

Answers
Answer:the heck
Step-by-step explanation:
the heck
The area of the base is 7 cm. What is the surface area of the pyramid?

Answers
Answer: 34.5
Step-by-step explanation:
(Base · Height) ÷ 2 → (2 · 4.5) ÷ 2 = 5.5
5.5 · 5 = 27.5
27.5 + 7 = 34.5
The early finish times for activities l, m, and p are 35, 27, and 33, respectively. What is the early finish time for activity t?
Answers
The early finish time for activity t is unknown and needs to be determined. It cannot be determined from the given information as only the early finish times for activities l, m, and p are given.
To determine the early finish time for activity t, the following steps should be taken:
1. Review the activities that are related to activity t and note their durations.
2. Identify the activities that must be completed before activity t can begin.
3. Calculate the early start time for activity t by adding the duration of all preceding activities.
4. Calculate the early finish time for activity t by adding the early start time and the duration of activity t.
5. Compare the early finish times of activities l, m, and p to the early finish time of activity t.
6. If the early finish time for activity t is greater than any of the other activities, then activity t is the critical activity.
7. If the early finish time for activity t is less than any of the other activities, then activity t is not the critical activity.
8. If the early finish time for activity t is equal to any of the other activities, then activity t could be the critical activity and further investigation is required.
Learn more about time here
https://brainly.com/question/8435652
#SPJ4
A vase has 3 red roses, 4 pink roses, and 5 white roses. Another vase has 2 red roses, 2 pink roses, and 2 white roses. If one rose is to be selected at random from each vase, what is the probability that both roses will be the same color
Answers
Answer:
The probability that both roses are red 1/12.
The probability that both roses are pink is 1/9.
The probability that both roses are white is 5/36.
Adding these probabilities together, we get 11/36.
So the probability that both roses will be the same color is 11/36.
Step-by-step explanation:
magine we are throwing a loaded die (6 sides). the probability that the die shows a 6 is twice as high as the probability of each of the other numbers. on average, out of these 70 throws how many times would the die show the number 6?
Answers
On solving the provided question, we can say that the probability is 6 out of 70 throws. =70*(2/7) =20
What is probability?Probability theory, a subfield of mathematics, gauges the likelihood of an occurrence or a claim being true. An event's probability is a number between 0 and 1, where approximately 0 indicates how unlikely the event is to occur and 1 indicates certainty. A probability is a numerical representation of the likelihood or likelihood that a particular event will occur. Alternative ways to express probabilities are as percentages from 0% to 100% or from 0 to 1. the percentage of occurrences in a complete set of equally likely possibilities that result in a certain occurrence compared to the total number of outcomes.
The likelihood of each side of a dice is one sixth, but
The likelihood that the die lands on a 6 is twice as likely as the likelihood of any other number.
The odds of 6 are 2/7 while the odds of the other numbers are 1/7.
We have 70 die throws.
the probability is 6 out of 70 throws.
=70*(2/7)
=20
To know more about probability visit:
https://brainly.com/question/11234923
#SPJ4
ms. forsythe gave the same algebra test to her three classes. the first class averaged $80\%$, the second class averaged $85\%$, and the third $89\%$. together, the first two classes averaged $83\%$, and the second and third classes together averaged $87\%$. what was the average for all three classes combined? express your answer to the nearest hundredth.
Answers
Let x= the average for all three classes combined. So x=85.25.
What is average?When you add two or more numbers and divide the result by the number of numbers you added together, you obtain an average.
How to calculate average?The arithmetic mean is determined by adding a collection of numbers, dividing by their count, and obtaining the result.
average = total points / number of students
total points = average*number of students
Let the total number of students in each class = a , b and x
The total number of points the first class amassed was 80a
The total number of points amassed by the second class was 85b
The total number of points amassed by the third class = 89c
For the first two classes we have
[ 80a + 85b ] / [ a + b] = 83
80a + 85b = 83a + 83b
subtract 80a, 83b from both sides
3a = 2b
a = 2/3b
For the second two classes we have
[ 85b + 89c ] / [ b + c ] = 87
[ 85b + 89c ] = 87 [b + c]
85b + 89c = 87b + 87c
subtract 85b, 87c from both sides
2c = 2b
b = c
For the three classes.....
Total points by all three classes / number of class members = the average for all three classes
[ 80a + 85b + 89c ] / [ a + b + c ] =[sub for a and c ]
[80 (2/3)b + 85b + 89b] / [ (2/3)b + b + b ]
b [ 80 (2/3) + 85 + 89 ] / [ b [( 2/3) + 1 + 1] ] [cancel the b's ]
[ 80 (2/3) + 85 + 89] [ 8/3 ]
[ 160/3 + 85 + 89 ] / [8/3] =
[ 160/3 + 255/3 + 267/3] / [8/3] multiply top/bottom by 3
[160 + 255 + 267 ] / 8 =
85.25 = average for all three classes
To learn more about average visit the link:
https://brainly.com/question/20118982
#SPJ4
Calculate the volume of oil exiting the pipe every hour: Calculate the volume of oil exiting the pipe every day: Convert cu in/day to cubic feet per day: cu. in/hour cu in/day cu ft/day
Answers
The volume of oil exiting the pipe is approximately 100 cu in/hr, 2,400 cu in/day, and 1.39 cu ft/day when converting cu in/day to cubic feet per day.
To calculate the volume of oil exiting the pipe every hour, you would need to know the flow rate of the oil in cubic inches per hour. Let's assume the flow rate is 100 cubic inches per hour.To find the volume of oil exiting the pipe every day, you would multiply the flow rate by the number of hours in a day. There are 24 hours in a day, so the volume of oil exiting the pipe every day would be 100 cubic inches per hour multiplied by 24 hours, which equals 2,400 cubic inches per day.
To convert the volume from cubic inches per day to cubic feet per day, you would need to divide the volume in cubic inches by the number of cubic inches in a cubic foot. There are 1,728 cubic inches in a cubic foot. So, dividing 2,400 cubic inches per day by 1,728 cubic inches per cubic foot, we get approximately 1.39 cubic feet per day.
Therefore, the volume of oil exiting the pipe is approximately 100 cubic inches per hour, 2,400 cubic inches per day, and 1.39 cubic feet per day.
To learn more about volume click here
brainly.com/question/22907480
#SPJ11
what is the critical value t* which satisfies the condition that the t distribution with 8 degrees of freedom has probability 0.10 to the right of t*?
Answers
To find the critical value t* for a t-distribution with 8 degrees of freedom, we need to use a t-table or a calculator with a t-distribution function. We want to find the value of t* such that the probability of getting a t-value greater than t* is 0.10 (or 10%).
Using a t-table, we can look for the row corresponding to 8 degrees of freedom and find the column that has a probability closest to 0.10. The closest probability in the table is 0.1002, which corresponds to a t-value of 1.859. Therefore, the critical value t* for a t-distribution with 8 degrees of freedom and a probability of 0.10 to the right of t* is approximately 1.859.
Alternatively, we can use a calculator with a t-distribution function to find the critical value. We can input the degrees of freedom (8) and the probability to the right of the critical value (0.10) into the calculator. The result is approximately 1.859.
In conclusion, the critical value t* for a t-distribution with 8 degrees of freedom and a probability of 0.10 to the right of t* is approximately 1.859.
To know more about Calculator visit :
https://brainly.com/question/30151794
#SPJ11
(a) Write an expression for a Riemann sum of a function f on an interval [a, b]. Explain the meaning of the notation that you use.
(b) If f(x)⩾ 0, what is the geometric interpretation of a Riemann sum? Illustrate with a diagram.
(c) If f(x) takes on both positive and negative values, what is the geometric interpretation of a Riemann sum? Illustrate with a diagram.
Answers
(a) The expression for a Riemann sum of a function f on an interval [a, b] is Δx = (b-a)/n
(b) If f(x)⩾ 0, then the geometric interpretation of a Riemann sum is infinity
(c) If f(x) takes on both positive and negative values, then the geometric interpretation of a Riemann sum is infinity
Riemann sums are an important tool in calculus for approximating the area under a curve. They are used to estimate the value of a definite integral, which represents the area bounded by the curve and the x-axis on a given interval. In this explanation, we will discuss the expression for a Riemann sum, its notation, and its geometric interpretation.
(a) Expression for a Riemann sum:
A Riemann sum is an approximation of the area under a curve using rectangles. We divide the interval [a, b] into n subintervals, each of length Δx=(b−a)/n. The notation used to represent this is:
Δx = (b-a)/n
(b) Geometric interpretation of a Riemann sum when f(x)⩾ 0:
If f(x) is always non-negative, the Riemann sum represents an approximation of the area between the curve and the x-axis on the interval [a, b].
Each rectangle has a positive area, which contributes to the overall area under the curve. The sum of the areas of the rectangles approaches the true area under the curve as the number of subintervals n approaches infinity.
(c) Geometric interpretation of a Riemann sum when f(x) takes on both positive and negative values:
When f(x) takes on both positive and negative values, the Riemann sum represents the net area between the curve and the x-axis on the interval [a, b].
Each rectangle may have a positive or negative area, depending on the sign of f(xi).
The positive areas represent regions where the curve is above the x-axis, and the negative areas represent regions where the curve is below the x-axis.
In conclusion, Riemann sums are used to approximate the area under a curve on an interval [a, b]. The expression for a Riemann sum involves dividing the interval into n subintervals and approximating the area under the curve using rectangles.
To know more about Riemann sum here.
https://brainly.com/question/30241844
#SPJ4