A survey found that the ratio of students who play intruments to those who do not was 7/20 of the students do not play an instrument 440 surveyd how many students surveyd play an instument
Answers
The number of students surveyed who plays an instrument is 114 students.
The ratio of students who play instruments to those who do not is 7/20, which means that out of every 7+20=27 students, 7 of them play an instrument and 20 of them do not.
If we know that 440 students were surveyed, we can set up a proportion to find the number of students who play an instrument:
7/27 = x/440
To solve for x, we can cross-multiply:
7 * 440 = 27 * x
3080 = 27x
x = 114.07
Since we can't have a fraction of a student, we should round up to the nearest whole number, which means that approximately 114 students surveyed play an instrument.
Therefore, the required answer is 114.
To know more about cross-multiply
https://brainly.com/question/28308012
#SPJ4
Related Questions
Plz help!! Will make brainliest

Answers
Answer:
-2x^2-6x-15=0
Step-by-step explanation:
Shift the 15 to the other side to get ax^2+bx+c
-2x^2-6x-15=0
What is the measurement of one exterior angle of a regular decagon?
Answers
Answer:
36 degrees
Step-by-step explanation:
A decagon is a 10 sided polygon. We can tell this because the prefix "deca-" stands for ten. To find the exterior angles of a regular polygon you can do 360 divided by the number of sides. Since there are 10 sides on a decagon, the equation is 360/10, which equals 36 degrees.
On the other hand, you can find the interior angles by using a different equation. The sum of the angles in a polygon is equal to 180(n-2) where n is the number of sides. So, a decagon has 1440 degrees. Then, to find the measure of each individual angle divide this number by the number of sides, 10. Thus, each angle is 144 degrees.
You can use this information to check the original answer. The interior angle plus the exterior angle should equal 180. Since 144+36=180, we know that the answer is correct.
System A
6x-y=-5
-6x+y=5
System B
x+3y=13
-x+3y=5
O The system has no solution.
The system has a unique solution:
(x, y) = (
The system has infinitely many solutions.
The system has no solution.
The system has a unique solution:
(x, y) = (
O The system has infinitely many solutions.
Answers
Answer:
Step-by-step explanation:
6x-y=-5
-6x+y=5
Adding the 2 equations we have:
0 + 0 = 0
0 = 0
This means there are infinite solutions
- the equations are identical.
System B
x+3y=13
-x+3y=5
Adding:
6y = 18
y = 3.
x = 13 - 3(3) = 4.
The system has a unique solution
(x. y) = (4, 3).
Please solve this question..
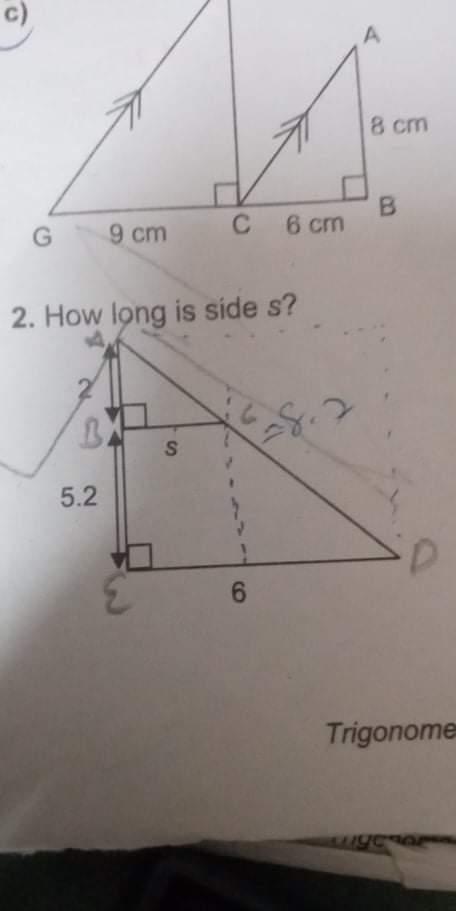
Answers
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
According to Thales theorem :
\( \frac{AB}{AE} = \frac{BC}{ED} \\ \)
\( \frac{2}{2 + 5.2} = \frac{s}{6} \\ \)
\( \frac{2}{7.2} = \frac{s}{6} \\ \)
\( \frac{1}{3.6} = \frac{s}{6} \\ \)
\( \frac{s}{6} = \frac{1}{3.6} \\ \)
Multiply sides by 6
\(6 \times \frac{s}{6} = 6 \times \frac{1}{3.6} \\ \)
Simplification
\(s = \frac{6}{3.6} \\ \)
\(s = \frac{6}{36 \times {10}^{ - 1} } \\ \)
\(s = \frac{6 \times {10}^{1} }{36} \\ \)
\(s = \frac{6 \times 2 \times 5}{6 \times 2 \times 3} \\ \)
6 s and 2 s are simplify
\(s = \frac{5}{3} \\ \)
\(s≈1.67\)
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
pls help asap if you can!!!

Answers
The statement that best proves that <XWY ≅ <ZYW is that two parallel lines are cut by a transversal, then the alternate interior angles are congruent
How to determine the statementTo determine the correct statement, we need to know the properties of a parallelogram.
These properties includes;
Opposite sides are parallel. Opposite sides are congruent. Opposite angles are congruent. Same-Side interior angles (consecutive angles) are supplementary. Each diagonal of a parallelogram separates it into two congruent triangles.The diagonals of a parallelogram bisect each other.Learn more about parallelogram at: https://brainly.com/question/10744696
#SPJ1
4. (NO CALC) Consider the differential equation dy/dx = x²-½y.(a) Find d²y/dx² in terms of x and y.
Answers
In summary d²y/dx² in terms of x and y is given by: d²y/dx² = 3/2 x + 1/4 y
Why is it?
To find d²y/dx², we need to differentiate the given differential equation with respect to x:
dy/dx = x² - 1/2 y
Differentiating both sides with respect to x:
d²y/dx² = d/dx(x² - 1/2 y)
d²y/dx² = d/dx(x²) - d/dx(1/2 y)
d²y/dx² = 2x - 1/2 d/dx(y)
Now, we need to express d/dx(y) in terms of x and y. To do this, we differentiate the original differential equation with respect to x:
dy/dx = x² - 1/2 y
d/dx(dy/dx) = d/dx(x² - 1/2 y)
d²y/dx² = 2x - 1/2 d/dx(y)
d²y/dx² = 2x - 1/2 (d²y/dx²)
Substituting this expression for d²y/dx² back into our previous equation, we get:
d²y/dx² = 2x - 1/2 (2x - 1/2 y)
d²y/dx² = 2x - x/2 + 1/4 y
d²y/dx² = 3/2 x + 1/4 y
Therefore, d²y/dx² in terms of x and y is given by:
d²y/dx² = 3/2 x + 1/4 y
To know more about Equation related question visit:
https://brainly.com/question/29657983
#SPJ1
Help please I need help. :)

Answers
Answer:
yes
Step-by-step explanation:
Find a basis for the space of 2x2 lower triangular matrices:
Answers
A basis for the space of 2x2 lower triangular matrices is \(\left(\left[\begin{array}{ccc}1&0\\0&0\end{array}\right],\left[\begin{array}{ccc}0&0\\1&0\end{array}\right],\left[\begin{array}{ccc}0&0\\0&1\end{array}\right]\right)\).
Lower triangular matrices resemble the following:
\(\left[\begin{array}{ccc}a&0\\b&c\end{array}\right]\)
We can write it like this:
\(a\left[\begin{array}{ccc}1&0\\0&0\end{array}\right]+b\left[\begin{array}{ccc}0&0\\1&0\end{array}\right]+c\left[\begin{array}{ccc}0&0\\0&1\end{array}\right]\)
This demonstrates the set's
\(\left(\left[\begin{array}{ccc}1&0\\0&0\end{array}\right],\left[\begin{array}{ccc}0&0\\1&0\end{array}\right],\left[\begin{array}{ccc}0&0\\0&1\end{array}\right]\right)\)
covers the set of lower triangular matrices with dimensions 2x2. Moreover, these are linearly independent, so attempting to
\(a\left[\begin{array}{ccc}1&0\\0&0\end{array}\right]+b\left[\begin{array}{ccc}0&0\\1&0\end{array}\right]+c\left[\begin{array}{ccc}0&0\\0&1\end{array}\right]=\left[\begin{array}{ccc}0&0\\0&0\end{array}\right]\)
leads to
\(\left[\begin{array}{ccc}a&0\\b&c\end{array}\right] =\left[\begin{array}{ccc}0&0\\0&0\end{array}\right]\)
which results in a = b = c = 0 right away. As there is no other way to
\(a\left[\begin{array}{ccc}1&0\\0&0\end{array}\right]+b\left[\begin{array}{ccc}0&0\\1&0\end{array}\right]+c\left[\begin{array}{ccc}0&0\\0&1\end{array}\right]=\left[\begin{array}{ccc}0&0\\0&0\end{array}\right]\)
, these matrices are linearly independent if a = b = c = 0.
Since
\(\left(\left[\begin{array}{ccc}1&0\\0&0\end{array}\right],\left[\begin{array}{ccc}0&0\\1&0\end{array}\right],\left[\begin{array}{ccc}0&0\\0&1\end{array}\right]\right)\)
they serve as a foundation by spanning the collection of 2x2 lower triangular matrices and being linearly independent.
To learn more about triangular matrices link is here
brainly.com/question/28325468
#SPJ4
The ratio of a to b is 4/7. If a is 16, find the value of b.
Answers
Answer:
B=28
Step-by-step explanation:
the mathematics part of the sat scores of students at utc are normally distributed with a mean of 500 and a standard deviation of 75.a. if 2.28 percent of the students who had the highest scores received scholarships, what was the minimum score among those who received scholarships? do not round your answer.
Answers
From standard normal distribution table, The minimum score among those who received scholarships was approximately 710.
To find the minimum score among those who received scholarships, we need to find the corresponding z-score using the standard normal distribution table.
Given that 2.28 percent of the students who had the highest scores received scholarships, we can find the z-score corresponding to this percentile. The z-score represents the number of standard deviations the score is above or below the mean.
Using a standard normal distribution table or a calculator, we find that the z-score corresponding to the 2.28th percentile is approximately -2.04.
Now, we can calculate the minimum score by using the z-score formula:
z = (x - mean) / standard deviation
Rearranging the formula, we can solve for x (the minimum score):
x = z * standard deviation + mean
Substituting the values:
x = -2.04 * 75 + 500
x ≈ 710
Therefore, the minimum score among those who received scholarships was approximately 710.
The minimum score among those who received scholarships was approximately 710 on the mathematics part of the SAT at UTC.
To know more about standard normal distribution table, visit
https://brainly.com/question/30404390
#SPJ11
A college professor hands out a list of 10 questions, 5 of which will appear on the final exam for the course. One of the students taking the course is pressed for time and can prepare for MATH 270 Assignment 2 W. Li 2 only 7 of the 10 questions on the list. Suppose the professor chooses the 5 questions at random from the 10. a) What is the probability that the student will be prepared for all 5 questions that appear on the final examination
Answers
Answer:
21 / 252
Step-by-step explanation:
Recall : nCr = n! ÷ (n-r)!r!
The total possible outcome ; 5 questions out of 10
10C5 = 10! ÷ 5!5! = (10*9*8*7*6)÷(5*4*3*2*1) = 252
Required outcome :
All 5 questions set being from the 7 questions covered and 0 from the 3 left uncovered
7C5 * 3C0
7C5 = 7! ÷ 2!5! = (7*6) ÷ (2*1) = 21
3C0 = 3! ÷ 3!0! = 1
Probability = required outcome / Total possible outcomes
P(All 5 questions prepared for appears) :
[7C5 * 3C0] ÷ 10C5
(21 * 1) / 252
= 21 / 252
Jim has 44 nickels and dimes totaling $2.95. How many nickels does he have?
Answers
29 Nickels
15 Dimes
Hope this is helpful!
-1+3 (10-12) to the third power divided by -16
Answers
Answer:
0.5
Step-by-step explanation:
-1+3(10-12)^3/-16
-1+3(-2)^3/-16
-1+(-24)/-16
.5
please help and thank u can u answer another question after this one?

Answers
Answer:
y = x^2
Explanation:
which of the following statements is/are true based on the graph of the function f (x) = –2^(–x – 2) + 2?
i. As x → [infinity], f (x) → 2.
ii. The x-intercept is (–2, 0).
iii. The function is an example of exponential decay.
a. I only
b. I and II only
c. I and III only
d. I, II, and III
Answers
The correct answer is c. I and III only.
Explanation:
i. As x → [infinity], f(x) → 2: This statement is true. As x approaches infinity, the exponential term -2^(-x - 2) approaches 0, and the constant term 2 remains. Therefore, the function approaches 2 as x approaches infinity.
ii. The x-intercept is (-2, 0): This statement is false. To find the x-intercept, we set f(x) = 0 and solve for x:
0 = -2^(-x - 2) + 2
2^(-x - 2) = 2
Taking the logarithm of both sides:
(x + 2) = log2(2)
(x + 2) = 1
x = -3
Therefore, the x-intercept is (-3, 0), not (-2, 0).
iii. The function is an example of exponential decay: This statement is true. The function f(x) = -2^(-x - 2) + 2 is a decreasing function as x increases. As x becomes larger, the exponential term -2^(-x - 2) becomes smaller, causing the function to approach 2, which is the horizontal asymptote. This behavior is characteristic of exponential decay.
In summary, based on the given options, statements i and iii are true, while statement ii is false. Therefore, the correct answer is c. I and III only.
Know more about Asymptote here:
https://brainly.com/question/32503997
#SPJ11
Someone plz help me :(

Answers
HELP PLEASE!!!!dont answer just for points:(

Answers
Answer:
15 is 50% of 30
and 75% of 20
write the equation of the set of all points equidistant from the line y=9 and fixed point (-2,5). must have sketch
Answers
Answer:
y = 7
Step-by-step explanation:
See the picture below.

please help me i have until midnight. im really stressed

Answers
Answer:
15/2= 7 1/2 =7.5
Step by step
Step 1 of 2: Add.
Add
5 and 2 over 165
2
16
+ 2 and 3 over 82
3
8
= 120 over 16
120
16
Step 1 of 2: Add, sub-step a: Convert mixed number to improper fraction.
Convert mixed number to improper fraction
5 and 2 over 165
2
16
= ( 5 × 16 ) over 16
5 × 16
16
+ 2 over 16
2
16
= ( 80 + 2 ) over 16
80 + 2
16
= 82 over 16
82
16
Step 1 of 2: Add, sub-step b: Convert mixed number to improper fraction.
Convert mixed number to improper fraction
2 and 3 over 82
3
8
= ( 2 × 8 ) over 8
2 × 8
8
+ 3 over 8
3
8
= ( 16 + 3 ) over 8
16 + 3
8
= 19 over 8
19
8
Step 1 of 2: Add, sub-step c: Find common denominator.
Find common denominator
82 over 16
82
16
+ 19 over 8
19
8
= ( 82 × 1 ) over ( 16 × 1 )
82 × 1
16 × 1
+ ( 19 × 2 ) over ( 8 × 2 )
19 × 2
8 × 2
= 82 over 16
82
16
+ 38 over 16
38
16
16 is the least common multiple of denominators 16 and 8. Use it to convert to equivalent fractions with this common denominator.
Step 1 of 2: Add, sub-step d: Add.
Add
82 over 16
82
16
+ 38 over 16
38
16
= ( 82 + 38 ) over 16
82 + 38
16
= 120 over 16
120
16
Step 1 of 2: Add.Hide
Step 2 of 2: Simplify.
Simplify
120 over 16
120
16
= 15 over 2
15
2
= 7 and 1 over 27
1
2
Step 2 of 2: Simplify, sub-step a: Reduce fraction to lowest terms.
Reduce fraction to lowest terms
120 over 16
120
16
= ( 120 ÷ 8 ) over ( 16 ÷ 8 )
120 ÷ 8
16 ÷ 8
= 15 over 2
15
2
8 is the greatest common divisor of 120 and 16. Reduce by dividing both numerator and denominator by 8.
Step 2 of 2: Simplify, sub-step b: Convert improper fraction to mixed number.
Convert improper fraction to mixed number
15 over 2
15
2
= 7 and 1 over 27
1
2
15 ÷ 2 = 7 remainder 1
Please show step by step how to solve the problem in Excel with the formula and not in Excel.
1.) Kate wants to purchase a car for $505.76 monthly payments for the next 5 years. Kate qualifies for a 4.3% loan. How much does the car cost?
Answer: 27,261
Use Excel to find PV (present value) of these monthly payments.
Excel PV formula: =PV(rate,nper,pmt,fv)
Use the number of monthly payments (years *12) for the nper and the monthly interest rate (rate/12).
Please show step by step how to solve the problem in Excel with the formula and not in Excel.
Answer: 437
2.) M wants to buy a used car for $23,099. If M wants to pay it off in 5 years, how much will she have to pay each month with an annual interest rate of 5.1%? Post answer as a positive amount.
PVOA = PMT x [1 - (1 /(1 + k)n ) / k] x ( 1 + k)
or use the PMT function in Excel. =PMT(rate,nper,pv,fv)
Remember for monthly payments, the nper = years * 12 and the annual interest rate must be divided by 12.
Thank you.
Answers
Problem 1
PMT = 505.76 = monthly payment
k = monthly interest rate in decimal form
k = 0.043/12 = 0.003583333 (approximate)
n = 5*12 = 60 months
PVOA = present value of ordinary annuity
PVOA = PMT * ( 1 - (1+k)^(-n) )/k
PVOA = 505.76 * ( 1 - (1+0.003583333)^(-60) )/0.003583333
PVOA = 27,261.436358296
When rounding to the nearest dollar, we get $27,261
Your teacher made a mistake in choosing the formula. S/he mixed up present value ordinary annuity with annuity due. The (1+k) portion at the end is ignored. I rewrote the 1/( (1+k)^n ) sub-portion as (1+k)^(-n) to avoid a bit of clutter.
--------
To type this into excel we will write
=PV(0.043/12,5*12,505.76,0,0)
That will produce the result of -27,261.44. The negative is to indicate a cash outflow.
Don't forget about the equal sign up front when writing excel formulas.
=====================================================
Problem 2
L = loan amount = 23099
k = interest rate per month = 0.051/12 = 0.00425 exactly
n = number of months = 5*12 = 60 months
PMT = monthly payment
PMT = (Lk)/(1 - (1 + k)^(-n) )
This formula is the result of solving PVOA = PMT * ( 1 - (1+k)^(-n) )/k for "PMT". The PVOA value is the loan amount in this case.
Let's plug in the values mentioned
PMT = (Lk)/(1 - (1 + k)^(-n) )
PMT = (23099*0.00425)/(1 - (1 + 0.00425)^(-60) )
PMT = 436.965684557303
PMT = 437 when rounding to the nearest whole number
--------
To do this in excel, we type in
=PMT(0.051/12,5*12,23099,0,0)
The output should be -436.97 which rounds to -437.
The value is negative to represent a cash outflow, but your teacher mentions to post the answer as a positive value.
Help please!!!!!!!!!!!!!!

Answers
Answer:
200=4hrs=10 of the machines
200=4hrs
300=xhrs
Cross multiply
200×xhrs = 300×4hrs
X=1200/200
X= 6 hours
Take a moment to think about what tan(θ) represents.Use interval notation to represent the values of θ (betwen 0 and 2π) where tan(θ)>1. Use interval notation to represent the values of θ (betwen 0 and 2π) where tan(θ)<−1.
Answers
ANSWERS
• tan(θ) > 1:, θ ,∈, {(π/4,, ,π/2) ∪ (5π/4, 3π/2)}
• tan(θ) < -1: ,θ ,∈, {(π/2, 3π/4) ∪ (3π/2, 7π/4)}
EXPLANATION
tan(θ) is a periodic function, that repeats its values between -π/2 and π/2.
When θ is close π/4, tan(θ) goes to infinity. The same happens for 5π/4, π/2 and 3π/2
Let's see the graph:
For θ between π/4 and π/2, the value of the tangent is more than 1. This is also true for θ between 5π/4 and 3π/2.
Then, when θ is between π/2 and 3π/4, and when it's between 3π/2 and 7π/4, tan(θ) is less htan -1.

which of the following is a way to increase the width of a confidence interval? a. increase the confidence level b. decrease the error c. increase the chance for error d. increase the sample size
Answers
If we want to increase the width of a confidence interval , we need to increase the confidence interval which will increase our z value
What is confidence interval?
In statistics, the probability that a population parameter will fall between a set of values for a predetermined percentage of the time is referred to as the confidence interval. Analysts frequently employ confidence ranges that include 95% or 99% of anticipated observations.
E=zs√n. The margin of error is represented by the quantity E. The margin of error is equal to the confidence interval's width divided by two. Occasionally, confidence intervals are expressed as x±E, for instance, 9.95±0.43.
Thus if we want to increase the width of a confidence interval , we need to increase the confidence interval which will increase our z value
To Learn more about the confidence interval form the link:
https://brainly.com/question/15712887
#SPJ1
what advantage does a study using multiple regression have over a study using bivariate correlation?
Answers
Multiple regression offers a more comprehensive and nuanced analysis by considering the influence of multiple predictors, capturing complex relationships, controlling for confounding variables, and enhancing predictive capabilities.
A study using multiple regression has several advantages over a study using bivariate correlation:
Multivariate analysis: Multiple regression allows for the inclusion of multiple predictor variables, which enables the examination of their individual contributions while controlling for the effects of other variables. This helps to identify the unique influence of each predictor on the outcome variable, considering their interrelationships.
Complex relationships: Multiple regression can capture complex relationships between variables by accounting for their combined effects. Bivariate correlation can only assess the linear relationship between two variables, whereas multiple regression can handle non-linear relationships and interactions between predictors.
Control of confounding variables: Multiple regression enables the control of confounding variables by including them as predictors in the model. By controlling for potential confounders, the relationship between the predictor and outcome variables can be more accurately assessed, reducing the likelihood of spurious associations.
Increased predictive power: Multiple regression can improve the predictive power of the model by incorporating multiple predictors. By considering multiple factors simultaneously, it can provide a more comprehensive understanding of the factors influencing the outcome variable and better predict its values.
Know more about Multiple regression here:
https://brainly.com/question/3737733
#SPJ11
Find the angle between the vectors u = 4i - 4j and v= - 4i +4j+ k The angle between the vectors is (Round to the nearest hundredth.) radians Find the angle between the vectors u = √5i - 9j and v= √5i+j-3k The angle between the vectors is radians. (Do not round until the final answer. Then round to the nearest hundredth as needed.)
Answers
Magnitude of vector u = √(5² + (-9)² + 0²) = √106 Magnitude of vector v = √(5² + 1² + (-3)²) = √35,Therefore,cos(θ) = (-4) / (√106) (√35)θ = cos⁻¹(-4 / (√106) (√35))= 2.38 radians (Do not round until the final answer. Then round to the nearest hundredth as needed.)
Given vectors are u
= 4i - 4j and v
= -4i + 4j + k.The angle between the vectors is radians.To find the angle between two vectors u and v, we use the following formula;cos(θ)
= (u.v) / |u| |v|where θ is the angle between vectors u and v, u.v is the dot product of vectors u and v, and |u| and |v| are the magnitudes of the respective vectors u and v.Dot Product: u.v
= (4)(-4) + (-4)(4) + (0)(1)
= -16 -16
= -32Magnitude of vector u
= √(4² + (-4)² + 0²)
= √32
Magnitude of vector v
= √((-4)² + 4² + 1²)
= √33 Therefore,cos(θ)
= (-32) / (√32) (√33)θ
= cos⁻¹(-32 / (√32) (√33))
= 2.18 radians (rounded to the nearest hundredth).The given vectors are u
= √5i - 9j and v
= √5i + j - 3k.
The angle between the vectors is radians.To find the angle between two vectors u and v, we use the following formula;cos(θ)
= (u.v) / |u| |v|where θ is the angle between vectors u and v, u.v is the dot product of vectors u and v, and |u| and |v| are the magnitudes of the respective vectors u and v.Dot Product: u.v
= (√5)(√5) + (-9)(1) + (0)(-3)
= 5 - 9 = -4.Magnitude of vector u
= √(5² + (-9)² + 0²)
= √106
Magnitude of vector v
= √(5² + 1² + (-3)²)
= √35
Therefore,cos(θ)
= (-4) / (√106) (√35)θ
= cos⁻¹(-4 / (√106) (√35))
= 2.38 radians (Do not round until the final answer. Then round to the nearest hundredth as needed.)
To know more about Magnitude visit:
https://brainly.com/question/31022175
#SPJ11
your statistics class has 26 students in it what is the probability that both students are girls given that the second student chosen is a girl
Answers
Given that the second student chosen is a girl, the probability that both students are female is 0.175.
The occurrence of likely events is referred to as probability. It is the branch of mathematics concerned with numerical estimates of the likelihood of an event occurring or a statement being true.
Probability is nothing but likelihood of something is to occur. When we are unsure about the outcome of an event, we can discuss the probabilities of certain outcomes—how likely they are.
The probability of selecting a girl from the class is
\(= \frac{Number\ of\ girls}{ Total\ number\ of\ students}= \frac{14}{26}\\\\= \frac{7}{13}\)
It is known that the one of the chosen student from 2 students is girl, the probability of having both girls will be:
\(= \frac{7}{16} * \frac{6}{15}\\\\= 0.175\)
Hence, the probability is 0.175.
To learn more about probability refer here
https://brainly.com/question/11234923
#SPJ4
Your question is incomplete, here is the complete question.
Your statistics class has 26 students in it - 14 girls and 12 boys.Your teacher uses a calculator to select two students at random to solve a problem on the board. Given that the second student chosen is a girl, what is the probability that the first student was also a girl?
The general equation for depreciation is given by y = A(1 – r)t, where y = current value, A = original cost, r = rate of depreciation, and t = time, in years. A car was purchased 6 years ago for $25,000. If the annual depreciation rate is 11%, which equation can be used to determine the approximate current value of the car?
Answers
Answer:
y=25,000(0.89)^6
Step-by-step explanation:
Answer:
a: y= 25,000(0.89)^6
Step-by-step explanation:
Graph the linear function w(x)=3/5x+2
All I need is the ordered pairs/points

Answers
9514 1404 393
Answer:
(0, 2), (5, 5)
Step-by-step explanation:
The w-intercept is the constant in the equation, so you know immediately that (x, w) = (0, 2) is one point on your graph.
Since the value of x is being multiplied by 3/5, it is convenient to choose an x-value that is a multiple of 5. When x=5, we have ...
w(5) = (3/5)(5) +2 = 3+2 = 5
So, (x, w) = (5, 5) is another point on your graph.

Find the area of triangle XYZ if length XY equals 7 and length XZ equals 4.3. You also
know that angle Y equals 79°.
Answers
Answer:
A ≈ 14.8 units²
Step-by-step explanation:
the area (A) of the triangle is calculated as
A = \(\frac{1}{2}\) yz sin Y ( that is 2 sides and the angle between them )
where x is the side opposite ∠ X and z the side opposite ∠ Z
here y = XZ = 4.3 and z = XY = 7 , then
A = \(\frac{1}{2}\) × 4.3 × 7 × sin79°
= 15.05 × sin79°
≈ 14.8 units² ( to 1 decimal place )
f(t)=e5t+4t+7ln(t2+3c)+te-1+5e6
where c is constant
Answers
The function f(t) is defined as e raised to the power 5t plus 4t plus the natural logarithm of the quantity t squared plus 3 times the constant c, raised to the power of 7, plus t times e raised to the power of -1 plus 5 times e raised to the power of 6.
Given a function:
f(t)=e5t+4t+7ln(t2+3c)+te-1+5e6
where c is a constant.
The solution to the question is shown below.
Step 1: We have given a function:
f(t)=e5t+4t+7ln(t2+3c)+te-1+5e6
We have to find the number of words we have to write to express this function in words.
Step 2: Solution
f(t) = et5+4t + ln(t²+3c)⁷ +te-1+5e⁶
Where,
et5+4t = exponential function
ln(t²+3c)⁷ = natural logarithmic function
te-1 = linear function
e⁶ = exponential function
Therefore, f(t) can be expressed in words as:
The function f(t) is defined as e raised to the power 5t plus 4t plus the natural logarithm of the quantity t squared plus 3 times the constant c, raised to the power of 7, plus t times e raised to the power of -1 plus 5 times e raised to the power of 6.
Step 3: Conclusion
Hence, the function f(t) can be expressed in words with:The function f(t) is defined as e raised to the power 5t plus 4t plus the natural logarithm of the quantity t squared plus 3 times the constant c, raised to the power of 7, plus t times e raised to the power of -1 plus 5 times e raised to the power of 6.
To know more about natural logarithm visit:
https://brainly.com/question/29154694
#SPJ11