A submarine travels 8.3 km due North from its base and then turns and travels due West for 13.9 km.
How far away is the submarine from its base?
Give your answer rounded to 1 DP
Answers
Answer:
He is 5.6 km away
Step-by-step explanation:
he starts traveling away from base and is 8.3 km away to start with
then he turns west and travels 13.9 km away
what this mean is that you have to subtract the distance he turned from the distance he started off with
ex: 13.9 - 8.3 = 5.9
to get your answer of how far away he is from the base
Related Questions
A bag of sand originally weighing 144 lb was lifted at a constant rate. As it rose, sand also leaked out at a constant rate. The sand was half gone by the time the bag had been lifted to 18 ft. How much work was done lifting the sand this far
Answers
Therefore, the work done in lifting the sand to a height of 18 ft is approximately 41,875.2 foot-pounds.
To calculate the work done in lifting the sand, we need to consider the weight of the sand that remains in the bag at a height of 18 ft.
Given that the bag originally weighed 144 lb, and it was half empty by the time it was lifted to a height of 18 ft, we can assume that half of the weight of the sand has been lost. Therefore, the weight of the sand remaining in the bag is 144 lb / 2 = 72 lb.
To calculate the work done in lifting the sand, we use the formula:
Work = Force × Distance
In this case, the force is equal to the weight of the sand remaining, and the distance is the height to which the sand was lifted.
The weight of the sand remaining is 72 lb, and the distance lifted is 18 ft. However, we need to convert the distance from feet to a more appropriate unit, such as joules. To do this, we need to multiply by the gravitational acceleration (approximated as 32.2 ft/s²) to obtain the distance in foot-pounds.
Distance in foot-pounds = 18 ft × 32.2 ft/s²
Now we can calculate the work:
Work = Force × Distance
= 72 lb × (18 ft × 32.2 ft/s²)
Calculating the value:
Work ≈ 72 lb × 581.6 ft·lb/s²
≈ 41,875.2 ft·lb
To know more about work done,
https://brainly.com/question/28729796
#SPJ11
Needed before 2/18/2022 || Geometry
Find m∠BFC

Answers
Answer:
∠BFC: 94 degrees
Step-by-step explanation:
∠AFB: 86 degrees
to make up a straight line you need all angles to add up to 180 degrees
180 - 86 = 94
hope this helps! :- )
can someone help me with this please
2.3 + r = 7.9
r = ?
Answers
Answer:
r = 5.6
Step-by-step explanation:
To solve this problem, we need to isolate r on one side of the equation. To do this, we need to subtract 2.3 from both sides, giving us:
2.3 + r = 7.9
r = 5.6
So, r = 5.6
Hope this helped!
Answer:
5.6
Step-by-step explanation:
2.3+r=7.9
r=7.9-2.3
r=5.6
The base of a rectangular prism has dimensions measuring 8 feet by 17 feet. If the volume of the prism is 1,632 cubic feet, find the height of the prism.
Answers
Answer:
the answer is 12
Step-by-step explanation:
I had this work sheat and got the answer from the teacher
For the volume of the prism is 1,632 cubic feet, the height of the prism is,
⇒ H = 12 feet
What is Multiplication?To multiply means to add a number to itself a particular number of times. Multiplication can be viewed as a process of repeated addition.
.
Given that;
The base of a rectangular prism has dimensions measuring 8 feet by 17 feet.
And, the volume of the prism is 1,632 cubic feet.
Now, We know that;
Volume of prism = B x H
Where, B is base area and H is height.
Hence, We get;
Volume of prism = B x H
1632 = 8 x 17 x H
1632 = 136 H
H =1632 / 136
H = 12 feet
Thus, For the volume of the prism is 1,632 cubic feet, the height of the prism is,
⇒ H = 12 feet
Learn more about the multiplication visit:
https://brainly.com/question/10873737
#SPJ3
Consider the diagram and the paragraph proof below.
Given: Right △ABC as shown where CD is an altitude of the triangle
Prove: a2 + b2 = c2
Triangle A B C is shown. Angle A C B is a right angle. An altitude is drawn from point C to point D on side A B to form a right angle. The length of C B is a, the length of A C is b, the length of A B is c, the length of A D is e, the length of D B is f, and the length of C D is h.
Because △ABC and △CBD both have a right angle, and the same angle B is in both triangles, the triangles must be similar by AA. Likewise, △ABC and △ACD both have a right angle, and the same angle A is in both triangles, so they also must be similar by AA. The proportions StartFraction c Over a EndFraction = StartFraction a Over f EndFraction and StartFraction c Over b EndFraction = StartFraction b Over e EndFraction are true because they are ratios of corresponding parts of similar triangles. The two proportions can be rewritten as a2 = cf and b2 = ce. Adding b2 to both sides of first equation, a2 = cf, results in the equation a2 + b2 = cf + b2. Because b2 and ce are equal, ce can be substituted into the right side of the equation for b2, resulting in the equation a2 + b2 = cf + ce. Applying the converse of the distributive property results in the equation a2 + b2 = c(f + e).
Which is the last sentence of the proof?
Because f + e = 1, a2 + b2 = c2.
Because f + e = c, a2 + b2 = c2.
Because a2 + b2 = c2, f + e = c.
Because a2 + b2 = c2, f + e = 1
Answers
The last sentence of the proof states, "By the Pythagorean theorem, since a squared plus b squared equals c squared, the sum of f and e is equal to c."
The proof establishes the proportions and similarities between the triangles in the diagram. It shows that the ratios of corresponding sides in the similar triangles hold true, leading to the proportions a/c = c/a and b/c = c/e. These proportions can be rearranged to obtain a2 = cf and b2 = ce.
The next step in the proof adds b2 to both sides of the equation a2 = cf, resulting in a2 + b2 = cf + b2. Since b2 = ce, we substitute ce into the equation, giving us a2 + b2 = cf + ce.
The final step applies the converse of the distributive property, which states that if a + b = c, then a(b + d) = ab + ad. In this case, we have a2 + b2 = cf + ce, which can be rewritten as a2 + b2 = c(f + e).
Therefore, the last sentence of the proof concludes that because a2 + b2 = c2 (as derived from the previous steps), it follows that f + e = c. This statement completes the proof and establishes the relationship between the lengths of the sides and the altitude in the right triangle. Option C is correct.
For more such question on Pythagorean theorem, . visit :
https://brainly.com/question/343682
#SPJ8
answer correctly and i’ll mark brainliest, pls help
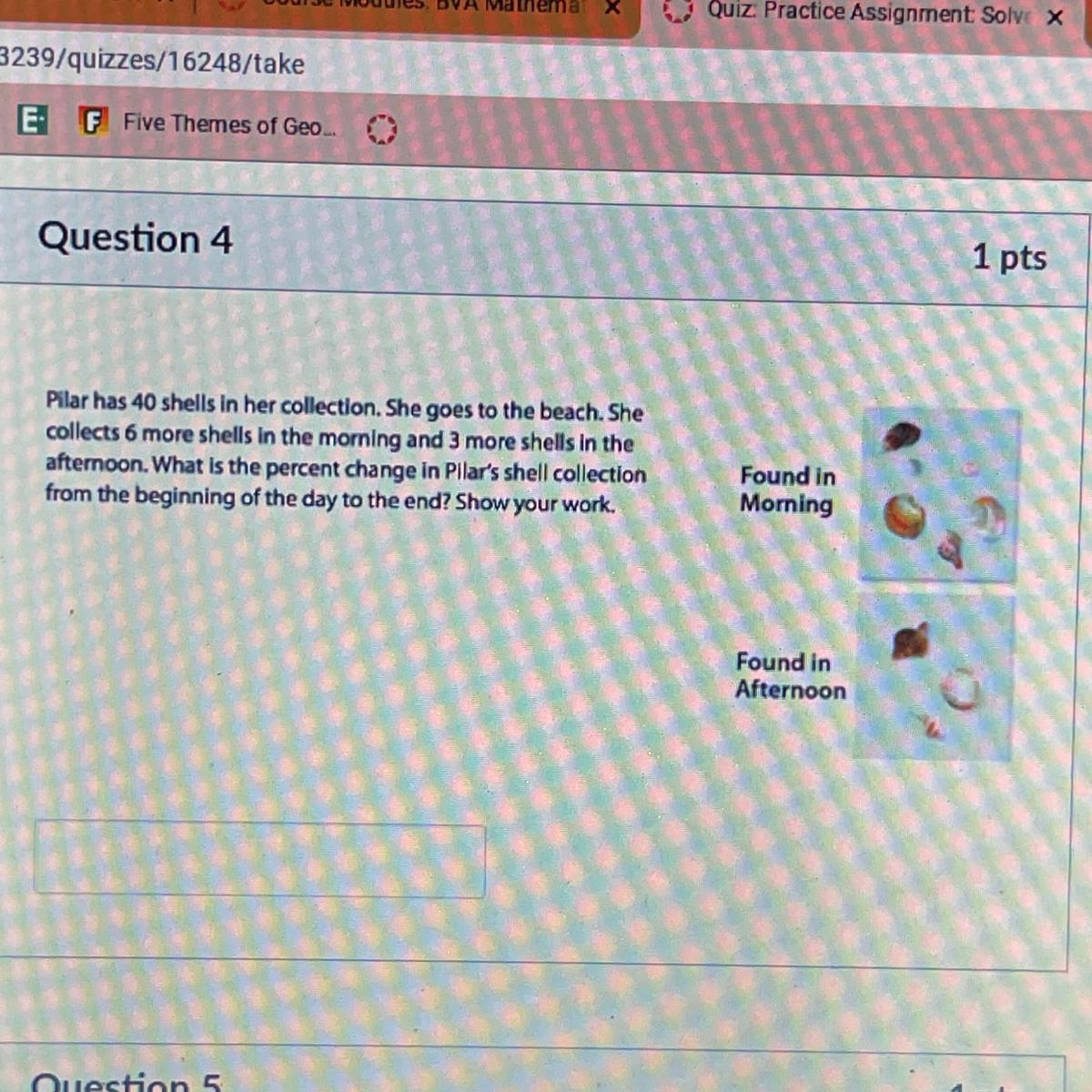
Answers
Answer:
22.5% increase.
Step-by-step explanation:
Because her collection grows by 9, that means it increases by 9/40 total. As a decimal, this would be 0.225. Then, as a percent you multiply that by 100 to get 22.5%. Pilar's collection increased by 22.5%
Answer:
hahaha is
easy hmm..........
Karina gets a 3% interest rate per year for her savings account. She has $8,500 in her savings account. How much money does she have in her account after 1 year?
Answers
Answer:8755
Step-by-step explanation:100%+3%=103% in decimal form 1.03
8500x1.03=8755
Which is equivalent to 23?
A
A 2
B
N
2
D
IN
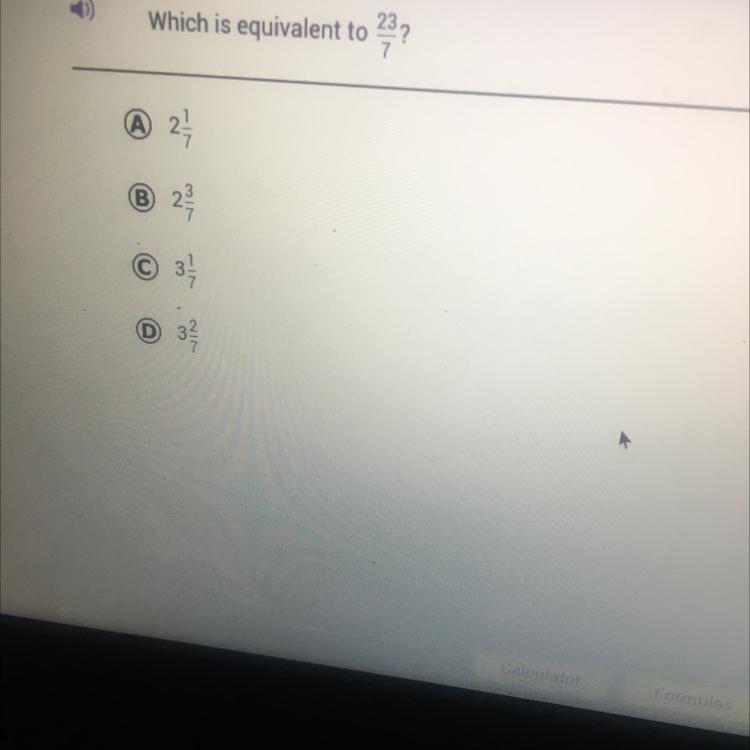
Answers
Find an expression which represents the sum of (3x - 3) and (-4x - 9) in
simplest terms.
Answers
Answer:
(-x - 12)
Step-by-step explanation:
(3x - 3) + (-4x - 9)
(3x-4x) + (-3-9)
-x+(-12)
(-x-12)
For what values of k does the function y = cos(kt) satisfy the differential equation 16y'' = −25y? (Enter your answers as a comma-separated list.)
Answers
The required answer are k = 5/4 and k = -5/4.
To determine the values of k that make the function y = cos(kt) satisfy the differential equation 16y'' = -25y, we need to substitute y = cos(kt) into the differential equation and solve for k.
First, find the second derivative of y = cos(kt). The first derivative is obtained by using the chain rule: y' = -ksin(kt), and the second derivative is y'' = -k^2cos(kt).
Now, substitute y = cos(kt) and y'' = -k^2cos(kt) into the differential equation 16y'' = -25y:
16(-k^2cos(kt)) = -25(cos(kt))
Simplify the equation:
-16k^2cos(kt) = -25cos(kt)
Divide both sides of the equation by cos(kt) to eliminate it:
-16k^2 = -25
Solve for k:
k^2 = 25/16
Taking the square root of both sides:
k = ±5/4
Therefore, the values of k that make the function y = cos(kt) satisfy the differential equation 16y'' = -25y are k = 5/4 and k = -5/4.
To know about derivative . To click the link.
https://brainly.com/question/29144258.
#SPJ11
Question 6
Bobby has a new 100-foot leash for his pet bird. His bird is flying at the end of its leash at a 30° angle
from the horizon while Bobby holds the leash 5 feet in the air. Draw a picture and calculate how far
the bird is above the ground. Hint 30-60-90 Special Triangle
Answers
The bird is 55 ft above the ground
How to find her horizontal distance from the turtle?Trigonometry is a branch of mathematics dealing with the relationship between the ratios of the sides of a right-angled triangle with its angles.
Check the attached image for the drawing.
From the drawing:
sin 30° = x/100 (opposite/hypotenuse)
x = 100 * sin 30°
x = 50 ft
height of the bird above the ground = x + 5
height of the bird above the ground = 50 + 5 = 55 ft
Learn more about Trigonometry on:
brainly.com/question/11967894
#SPJ1

Consider the following sample data:
x 12 18 20 22 25
y 15 20 25 22 27
a. Calculate the covariance between the variables. (Round your intermediate calculations to 4 decimal places and final answer to 2 decimal places.)
Covariance b-1. Calculate the correlation coefficient. (Round your intermediate calculations to 4 decimal places and final answer to 2 decimal places.)
Answers
a. Covariance = 10.11
b. Correlation coefficient = 0.376
Considering the following sample data:
x 12 18 20 22 25
y 15 20 25 22 27
a. Calculation of covariance
Covariance can be calculated by the formula:
Cov (X, Y) = [Σ(X - μx) (Y - μy)] / n
where, Σ denotes the sum of, X and Y are the variables, μx and μy are the means of X and Y respectively, and n is the sample size.
x y x-μx y-μy (x-μx)(y-μy) (-)^2 (-)^2
12 15 -6.6 -5.6 37.12 43.56 31.36
18 20 -0.6 -0.6 0.36 0.36 0.36
20 25 1.4 4.4 6.16 1.96 19.36
22 22 3.4 -2.6 -8.84 11.56 6.76
25 27 6.4 2.4 15.36 41.16 5.76
Σx = 97, Σy = 109, Σ(x-μx) = 5.00, Σ(y-μy) = -2.00, Σ(x-μx)(y-μy) = 50.56
Covariance is: Cov (X, Y) = [Σ(X - μx) (Y - μy)] / n= 50.56/5= 10.11
Thus, the covariance between the variables is 10.11.
b-1. Calculation of correlation coefficient.
Correlation coefficient is a statistical measure that measures the degree to which two random variables are associated. It can be calculated by the formula:
= Cov (X, Y) / where, Cov (X, Y) is the covariance between X and Y, σX and σY are the standard deviations of X and Y respectively.
σx2 = [Σ(x-μx)2] / (n-1)σy2 = [Σ(y-μy)2] / (n-1)σx = √[Σ(x-μx)2] / (n-1)σy = √[Σ(y-μy)2] / (n-1)
x y (x-μx) (y-μy) (x-μx)2 (y-μy)2 (-)(-)
12 15 -6.6 -5.6 43.56 31.36 1
18 -0.6 -0.6 0.36 0.36 0.32 5
20 25 1.4 4.4 1.96 19.36 22
22 3.4 -2.6 11.56 6.76 -8.84 25
27 6.4 2.4 41.16 5.76 15.36
Σx = 97, Σy = 109, Σ(x-μx) = 5.00, Σ(y-μy) = -2.00, Σ(x-μx)(y-μy) = 50.56
σx2 = 30.70
σy2 = 25.70
σx = √30.70 = 5.54
σy = √25.70 = 5.07
Correlation coefficient is:
= Cov (X, Y) / = 10.11 / (5.54*5.07)= 0.376
Thus, the correlation coefficient is 0.376.
For more such questions on Covariance & Correlation coefficient.
https://brainly.com/question/2618552#
#SPJ11
Write a recursive formula for the arithmetic sequence:a={12,17,22,...}a_1=Answera_n = a_{n-1} + Answer

Answers
1) A Recursive formula refers always to the previous term.
2) In this Arithmetic Sequence, the common difference is 5, the first term is 12. So we can set the following Arithmetic Sequence:
\(\begin{gathered} a_{1}=\textbf{12} \\ a_2=12+5n \\ a_n=a_{n-1}+\textbf{5n} \end{gathered}\)Thus, this is the answer.
find f · dr c where c is a circle of radius 4 in the plane x y z = 3, centered at (1, 1, 1) and oriented clockwise when viewed from the origin. f = (z − y) i (x − z) j (y − x)k f · dr c =
Answers
The value of \(f · dr_c\) is 32π.
What is the value of \(f · dr_c\)?To find \(f · dr_c\), we need to first find the vector field f and the line integral \(dr_c.\)
The vector field f is given by:
\(f = (z − y) i + (x − z) j + (y − x) k\)
The line integral \(dr_c\) can be parameterized using the equation of the circle of radius 4 centered at (1, 1, 1) in the plane x y z = 3:
\(r(t) = 4 cos(t) i + 4 sin(t) j + (3 - 4 cos(t) - 4 sin(t)) k\), where 0 ≤ t ≤ 2π.
Taking the differential of r(t), we get:
\(dr = (-4 sin(t)) i + (4 cos(t)) j + 4 sin(t) k\)
Now we can evaluate the dot product \(f · dr\):
\(f · dr = (z − y) dx + (x − z) dy + (y − x) dz\)
\(= [(3 - 4 cos(t) - 4 sin(t)) - 4 sin(t)] (-4 sin(t)) + [4 cos(t) - (3 - 4 cos(t) - 4 sin(t))] (4 cos(t)) + [(4 sin(t) - 4 cos(t))] (4 sin(t))\)
=\(-32 sin^2(t) + 32 cos^2(t) + 0\)
\(= 32 cos^2(t) - 32 sin^2(t)\)
Since the circle is oriented clockwise when viewed from the origin, we need to reverse the direction of the parameterization by replacing t with -t. Therefore, we have:
\(f · dr_c\) = ∫\(_0^(2π) (32 cos^2(-t) - 32 sin^2(-t)) dt\)
\(=\)∫\(_0^(2π) (32 cos^2(t) - 32 sin^2(t)) dt\)
\(= 32(\)π\(cos(0) - π sin(0))\)
\(= 32\)π
Hence, the value of \(f · dr_c is 32\)π.
Learn more about parameterization
brainly.com/question/31055234
#SPJ11
In ABC, a = 4, b = 3, and c = 3. What is the
value of cos A?

Answers
The value of cos A in the triangle is 1 / 9.
How to find the angle of a triangle?The triangle is given as ABC. The side lengths are a, b and c. Therefore, cos A of the triangle can be found using cosine rule as follows:
a² = b² + c² - 2bc cos A
a = 4
b = 3
c = 3
Therefore,
4² = 3² + 3² - 2(3)(3) cos A
16 = 9 + 9 - 18 cos A
16 - 18 = - 18 cos A
-2 = - 18 cos A
divide both sides by - 18
cos A = - 2 / - 18
cos A = 1 / 9
learn more on triangle here:https://brainly.com/question/16800749
#SPJ1
A food truck sells hamburgers and hotdogs in the ratio of 6 to 8, meaning that for every 6 hamburgers sold, 8 hotdogs are sold. on a given day, there were 14 more hot dogs sold than hamburgers. given this information, determine how many of each were sold.
Answers
The food truck sold 42 hamburgers and 56 hotdogs.
Let's use algebra to solve this problem. Let x be the number of hamburgers sold and y be the number of hotdogs sold. We can set up a system of equations based on the information given:
The ratio of hamburgers to hotdogs sold is 6:8, or simplified, 3:4:
x/y = 3/4
There were 14 more hotdogs sold than hamburgers:
y = x + 14
Now we can substitute the second equation into the first equation and solve for x:
x/(x+14) = 3/4
4x = 3(x+14)
4x = 3x + 42
x = 42
So 42 hamburgers were sold. We can use the second equation to find the number of hotdogs sold:
y = x + 14
y = 42 + 14
y = 56
So 56 hotdogs were sold. Therefore, the food truck sold 42 hamburgers and 56 hotdogs.
Learn more about truck here
https://brainly.com/question/29149735
#SPJ11
-3 {2x - 8} = 2x what is the value of x
Answers
Answer:
x = 3
Step-by-step explanation:
First, distribute the -3 to each term in the parentheses. Now, you have
-6x + 24 = 2x. Add 6x to both sides, and now you have 24= 8x. Divide both sides by 8, and now you get x=3.
If there is no joint variability between two variables, then the r value will be?
Answers
Answer:
If r=0, there is absolutely no relationship between the two variables.
Step-by-step explanation:
Please help!!!! My assignment is almost due!!!

Answers
Answer:
15
Step-by-step explanation:
the triangles are similar so will be the same proprotion,
I have attached a picture showing how I solved this. the second traingle is 3 times as large (15 by 12) compared to the first triangle which is 4 by 5.

türk olan var mı
yani benden başka
Answers
Answer:
English translation please.....
(1 point) a poll is taken in which 302 out of 525 randomly selected voters indicated their preference for a certain candidate. (a) find a 95% confidence interval for p.
Answers
Using the standard z table, a 95% confidence interval for p is (0.5327,0.6173).
In the given question,
A poll is taken in which 302 out of 525 randomly selected voters indicated their preference for a certain candidate.
We have to find a 95% confidence interval for p.
From the question, x=302, n=525
So estimation point,
P=x/n
P=302/525
P=0.575
Now the z value of 95% confidence interval is 1.960 using the standard z table.
Margin of Error (E)=z×√{P(1−P)}/n
Now putting the value
E=1.960×√{0.575(1−0.575)}/525
E=1.960×√(0.575×0.425)/525
E=1.960×√0.244/525
E=1.960×√0.000465
E=1.960×0.0216
E=0.0423
At 95% confidence interval for p is
P−E ≤ p ≤ P+E
Now putting the value
0.575−0.0423≤ p ≤0.575+0.0423
0.5327≤ p ≤0.6173
Hence, a 95% confidence interval for p is (0.5327,0.6173).
To learn more about confidence interval link is here
brainly.com/question/24131141
#SPJ4
input output f(x)= -5(x+7)
Answers
Answer:
x= -7
Step-by-step explanation:
f(x) = -5(x+7)
0 = -5x -35
5x = -35
equals to x= -7
Can you please help me out with a question
Answers
We have that in this case, we have that the measure of an angle on a circle is half the measure of its intercepted arc.
We have that the whole circle corresponds to a 360º, then:
because 360º - 214º = 144º
Then, the the intercepted arc by the angle K is 144º.
Then,
\(\angle K=\frac{144º}{2}=72º\)Answer: D. 72º
I need some serious help with some problems there are some on my profile and this one

Answers
Answer:
a) 28
b) D
Step-by-step explanation:
a) As you can see from the diagram, in a 60-30 right triangle, the side adjacent to the 60° angle is half of the hypotenuse.
14*2=28
b) If you remember your SohCahToa, then you'll know that your trigonometric functions are:
\(sin = \frac{opp}{hyp}\\cos = \frac{adj}{hyp}\\tan = \frac{sin}{cos}\)
Now we can check each one to find the incorrect ratio:
\(sin (30^o)=\frac{4}{8}=\frac{4}{8}\\cos(60^o)=\frac{4}{8}=\frac{4}{8}\\sin(60^o)=\frac{\sqrt{48}}{8}=\frac{\sqrt{48}}{8}\\tan(30^o)=\frac{4}{\sqrt{48}}\neq \frac{\sqrt{48}}{8}\)

Could someone please answer these 2

Answers
Answer:
A. 1/6
B. 1
Step-by-step explanation:
A. 9/j x j/54= 9/54 = 1/6
B. 6k/8m : 3k/4m = 6k/8m : 4m / 3k = 2/2 =1
Answer:
a. 3/2
b. 1
Step-by-step explanation:
A. To simplify the expression, we can cancel out the common factor of j:
9/j * j/54 = (9/1 * 1/6) = 3/2
Therefore, 9/j * j/54 simplifies to 3/2.
B. To divide fractions, we can multiply the first fraction by the reciprocal of the second fraction. That is,
(a/b) ÷ (c/d) = (a/b) x (d/c)
Using this rule, we can simplify the given expression as follows:
6k/8m ÷ 3k/4m = (6k/8m) x (4m/3k)
= (6/8) x (4/3)
= 2/2
= 1
In a recent year, 33.9% of all registered doctors were female. If there were 44,800 female registered doctors that year, what was the total number of registered doctors? Round your answer to the nearest whole number.
Answers
Answer:
wrong
Step-by-step explanation:
What is an equation of the line that passes through the points
(
−
4
,
−
3
)
(−4,−3) and
(
7
,
8
)
(7,8)?
Answers
The equation of the line that passes through the points (-4, -3) and (7, 8) is:
y = x + 1
To find the equation of a line that passes through two points, we can use the slope-intercept form of a linear equation, which is:
y = mx + b
where m is the slope of the line and b is the y-intercept.
First, let's find the slope (m) using the two given points: (-4, -3) and (7, 8).
The slope (m) is calculated as:
m = (y2 - y1) / (x2 - x1)
m = (8 - (-3)) / (7 - (-4))
m = (8 + 3) / (7 + 4)
m = 11 / 11
m = 1
Now that we have the slope (m), we can substitute one of the given points and the slope into the slope-intercept form to find the y-intercept (b).
Using the point (-4, -3):
-3 = (1)(-4) + b
-3 = -4 + b
b = -3 + 4
b = 1
Therefore, the equation of the line that passes through the points (-4, -3) and (7, 8) is:
y = x + 1
For such more questions on Line Equation Calculation
https://brainly.com/question/30097527
#SPJ8
find the slope between points (-4,7) (2,-5)
Answers
Answer: -2
Step-by-step explanation:
\(\frac{y2 - y1}{x2 - x1}\) = \(\frac{7-(-5)}{-4-2}\) = \(\frac{12}{-6}\) = -2
how many times larger is a centigram than a milligram? 10times | 100 times| 1000 times| 0.1 time
Answers
A centigram is 100 times larger than a milligram. So, the option b) 100 times is correct for this question.
1 centigram = 100 milligrams. A centigram is a unit of mass in the metric system, equivalent to one hundredth of a gram. A milligram, on the other hand, is a unit of mass in the metric system, equivalent to one thousandth of a gram. Therefore, a centigram is 100 times larger than a milligram. The conversion between the two units can be easily calculated as 1 centigram is equal to 100 milligrams. The use of centigrams is limited in common applications, with milligrams being the preferred unit for expressing very small masses, while grams and kilograms are used for larger masses.
To learn more about centigram click here
brainly.com/question/16594542
#SPJ4
Calculate the volume of the cuboid shown below. 3 Give your answer in cm cm³. If your answer is a decimal, then round it to 1 d.p. 4 cm 19 cm 21 cm Not drawn accurately

Answers
Note that the volume of the cuboid is approximately 1,974.08 cm³.
How is this so?To find the volume of a cuboid,you need to multiply its length (L), height (H), and width (W) together.
In this case, the length (L) is given as 19 cm, the height (H) is given as 4 cm, and the diagonal represents the hypotenuse of a right-angled triangle formed by the length, height,and width of the cuboid.
Using the Pythagorean theorem, we can determine the width (W) of the cuboid -
Width (W) = √(Diagonal² - Height²)
= √(21² - 4²)
= √(441 - 16)
= √425
≈ 20.62 cm
Now that we have the values for L, H, and W, we can calculate the volume (V) of the cuboid -
Volume (V) = Length (L) * Height (H) * Width (W)
= 19 cm * 4 cm * 20.62 cm
≈ 1,974.08 cm³
Therefore, the volume of the cuboid is approximately 1,974.08 cm³.
Learn more about volume at:
https://brainly.com/question/27710307
#SPJ1