A student on the track team runs 45 minutes each day as a part of her training. She begins her workout by running at a constant rate of 8 miles per hour for a minutes, then slows to a constant rate of 7.5 miles per hour for b minutes.
Which equation describes the relationship between the distance she runs in miles, D, and her running speed, in miles per hour?
8a+7.5b=D8a+7.5b=D
Answers
The equation that describes the relationship between the distance she runs in miles, \(D\),and her running speed, \(b\), in miles per hour is \(D = 8(45 - b) + 7.5b\).
So, option \(D\) is correct.
\(\textup{Speed} = \frac{\textup{Distance}}{\textup{Time}}\)
So, \(\textup{Distance} = \textup{Speed} \times \textup{Time}\)
She begins her workout by running at a constant rate of miles per hour for \(a\) minutes, then slows to a constant rate of miles per hour for \(b\) minutes.
\(D=8 a + 7.5 b...(i)\)
Also, \(a+b=45\)
So, \(a=45-b\)
Substitute the value of \(a\) in \((i)\)
\(D=8 (45-b) + 7.5 b\)
So, the correct equation is \(D=8 (45-b) + 7.5 b\).
Learn more about speed here:
https://brainly.com/question/23774048?referrer=searchResults
Related Questions
The height at time t (in seconds) of a mass, oscillating at the end of a spring, is s(t) = 300 + 16 sin t cm. Find the velocity and acceleration at t = pi/3 s. v(pi/3) = a(pi/3) =
Answers
The height at time t (in seconds) of a mass, oscillating at the end of a spring, is s(t) = 300 + 16 sin t cm. We have to find the velocity and acceleration at t = π/3 s.
Let's first find the velocity of the mass. The velocity of the mass is given by the derivative of the position of the mass with respect to time.t = π/3 s
s(t) = 300 + 16 sin t cm
Differentiating both sides of the above equation with respect to time
v(t) = s'(t) = 16 cos t cm/s
Now, let's substitute t = π/3 in the above equation,
v(π/3) = 16 cos (π/3) cm/s
v(π/3) = -8√3 cm/s
Now, let's find the acceleration of the mass. The acceleration of the mass is given by the derivative of the velocity of the mass with respect to time.t = π/3 s
v(t) = 16 cos t cm/s
Differentiating both sides of the above equation with respect to time
a(t) = v'(t) = -16 sin t cm/s²
Now, let's substitute t = π/3 in the above equation,
a(π/3) = -16 sin (π/3) cm/s²
a(π/3) = -8 cm/s²
Given, s(t) = 300 + 16 sin t cm, the height of the mass oscillating at the end of a spring. We need to find the velocity and acceleration of the mass at t = π/3 s.
Using the above concept, we can find the velocity and acceleration of the mass. Therefore, the velocity of the mass at t = π/3 s is v(π/3) = -8√3 cm/s, and the acceleration of the mass at t = π/3 s is a(π/3) = -8 cm/s².
At time t = π/3 s, the velocity of the mass is -8√3 cm/s, and the acceleration of the mass is -8 cm/s².
To know more about mass visit
https://brainly.com/question/20579920
#SPJ11
use th result of part (a) to determine the value of the richardson's error estimate of t32, t64, and t128.
Answers
The computed area values of Tₐ(f) for \( \int_{0}^{4} \frac{ 1}{1 + x²} dx = tan^{-1} (-4) = 1.32581766366803 \\ \), are equal to 1.2500, 1.3100, 1.3182, 1.3221, 1.3240. The value of Richardson's error estimate for T₃₂, T₆₄, and T₁₂₈ are 6.5104× 10⁻⁴, 1.6276× 10⁻⁴ and 4.0690× 10⁻⁵ respectively.
The trapezoidal rule is a numerical method for approximating the definite integral of a function f(x) over an interval [a, b]. It estimates a definite integral by dividing the area under the curve into a series of trapezoids, and then summing up all. The MatLab script or program to implement Trapezoidal Rule is written as :
a= 0;
b = 4;
n= input ('Enter n ');
h=(b-a)/n;
sum = 0.0;
% to find the sum
%dx = (b-a)/(n-1);
% To find step size or height of trapezium
% Generating the samples
for i = 1: n
x(i) = a + (i-1) ×h ;
end
% Generate the function value at different values of x or sample
for i = 1:n
\(y(i) = 1./(1+x(i).^2);\)
end
% Computation of area by using method 1
for i = 1:n
if ( i == 1 || i == n) % for finding the sum of fist and last ordinate
sum = sum + y(i)./2;
else
sum = sum + y(i); % for calculating the sum of other ordinates
end
end
area = sum * h
Output
Enter n = 4
area = 1.2500
>> Trapz
Enter n 16
area = 1.3100
>> Trapz
Enter n 32
area = 1.3182
>> Trapz
Enter n 64
area = 1.3221
>> Trapz
Enter n 128
area = 1.3240
b)
\(f(x)=\frac{1}{(x^2+1)} \newline\)
\(f''(x)=\frac{(6x^2-2)}{(x^2+1)^3} \newline\)
We have to find max f''(x) for x in [0,4] \newline
\(f'''(x)=\frac{(-24x^3+24x)}{(x^2+1)^4}\)
Now, f'''(x)=0 will lead to x=0, 1 f''''(1)< -3 <0, f''(x) has maximum value at x=1
\(max f''(x)=f''(1)=\frac{1}{2}(=M, say) \\ \)
Error Formula is written as: \(T_n=\frac{h^2(b-a)}{12}M=\frac{(b-a)^3}{12n^2}M\) (\because nh=b-a). Now, the program is written as following, Program :
n= input ('Enter n');
E=4^2/(12*n^2)*(1/2)
Output
>> Error_Trapz
Enter n 32
E = 6.5104e-04
>> Error_Trapz
Enter n 64
E = 1.6276e-04
>> Error_Trapz
Enter n 128
E =4.0690e-05
>>
Hence, required error values are 6.5104× 10⁻⁴, 1.6276× 10⁻⁴ and 4.0690× 10⁻⁵.
For more information about Richardson's error estimate, visit :
https://brainly.com/question/30451696
#SPJ4
Complete question:
(a) Write a MatLab script to implement the Trapezoidal Rule. Hence, compute the value of a,(f) for
\( \int_{0}^{4} \frac{ 1}{1 + x²} dx = tan^{-1} (-4) = 1.32581766366803 \\ \)
, for n = 4,8,16,...128.
(b) Use the result of part (a) to determine the value of the Richardson's error estimate for T32, T64 , and , T128 In your solution include a copy of the Trapezoidal Rule script.
PLZ HELP WUICK ILL MARK BRAINLEIST!!!
15. a) Target sells cases of Mountain Dew for $3 if you buy a Target Red
Card for $20. Walmart sells cases of Mountain Dew for $5. Choose the
equation that can be used to determine how many cases will it take for the
cost to be the same?
3x + 20 = 5x
8x = 20
ОА
OB
8x + 20 = 0
3x - 20 = 5
D
Answers
Answer:
3x - 20 = 5
Step-by-step explanation:
Before investing the fund, you would like to know more about the fund manager’s investment strategy. To obtain more information, you choose to use the Style analysis technique. Based on the regression output below for a range of asset classes, what is/are the major portfolio strategies of this fund? Please explain your answers. Do the asset allocation strategies explain majority of the return variabilities?
Style Portfolio Regression Coefficient P-values
Small Cap 0.0003 0.9243
Medium Cap 0.3560 0.1150
Large Cap 0.4231 0.0080
Low Book-to-
Market (Growth) 0.1346 0.2141
High Book-to-
Market (Value) 0.5531 0.0013
R-square 0.3500
Answers
The major portfolio strategies of this fund are investing in large-cap stocks and value stocks with high book-to-market ratios. The regression coefficients and p-values provide insights into the fund manager's investment strategy.
The coefficient of 0.4231 for the Large Cap asset class is statistically significant with a p-value of 0.0080, indicating a significant allocation to large-cap stocks. Additionally, the coefficient of 0.5531 for the High Book-to-Market (Value) asset class is also statistically significant with a p-value of 0.0013, indicating a significant allocation to value stocks with high book-to-market ratios.
These findings suggest that the fund manager focuses on investing in large-cap stocks and value stocks with high book-to-market ratios as part of their portfolio strategy.
Regarding the explanation of return variabilities, the R-square value of 0.3500 indicates that the asset allocation strategies explained 35% of the return variabilities in the fund. While this is a significant portion, it also implies that other factors not captured by the regression analysis contribute to the remaining 65% of return variabilities. Therefore, while the asset allocation strategies explain a substantial portion of return variabilities, other factors also play a role in determining the overall returns of the fund.
Learn more about large-cap stocks here: brainly.com/question/29458217
#SPJ11
A shipping container is in the form of a right rectangular prism, with dimensions of 30 ft by 8 ft by 7 ft 3 in. If the container holds 1096 cubic feet of shipped goods, what percent is empty?
Answers
As per the volume of a rectangular prism, it is found that 34.76% of the container is empty.
Volume of a rectangular prism
The volume of the rectangle prism is calculated by multiplying the length, breadth and height of the prism.
The formula for the volume of rectangle prism is
V = l x w x h
where
l represents the length
w represents the width
h represents the height
Given,
A shipping container is in the form of a right rectangular prism, with dimensions of 30 ft by 8 ft by 7 ft 3 in.
Here we need to find if the container holds 1096 cubic feet of shipped goods, what percent is empty
According to the given question,
Let us consider the length is 30ft, Width is 8ft and Height is 7ft.
Here the value 3ft refers the depth.
That one is also multiplied with the volume.
Therefore, the volume of the container is
=> 8 x 7 x 30
=> 1680
Therefore, the volume of the container is 1680 cubic feet.
So, here we have to percentage of the empty space for that we have to find the difference of them and convert it into percentage,
=> 1680 - 1096
=> 584
The percent of empty space is,
=> x% of 1680 = 584
=> x% = 584/1680
=> x% = 0.3476
=> x = 34.76
Therefore, 34.76% of rectangular prism container is empty.
To know more about Volume of rectangle prism here.
https://brainly.com/question/12702730
#SPJ1
what's the difference between the arithmetic and geometric average return (conceptually, not mathematically), and when is it best to use each?
Answers
Conceptually, the arithmetic and geometric average returns are different measures used to describe the performance of an investment or an asset over a specific period.
The arithmetic average return, also known as the mean return, is calculated by adding up all the individual returns and dividing by the number of periods. It represents the average return for each period independently.
On the other hand, the geometric average return, also called the compound annual growth rate (CAGR), considers the compounding effect of returns over time. It is calculated by taking the nth root of the total cumulative return, where n is the number of periods.
When to use each measure depends on the context and purpose of the analysis:
1. Arithmetic Average Return: This measure is typically used when you want to evaluate the average return for each individual period in isolation. It is useful for analyzing short-term returns, such as monthly or quarterly returns. The arithmetic average return provides a simple and straightforward way to assess the periodic performance of an investment.
2. Geometric Average Return: This measure is more suitable when you want to understand the compounded growth of an investment over an extended period. It is commonly used for long-term investment horizons, such as annual returns over multiple years.
The geometric average return provides a more accurate representation of the overall growth rate, accounting for the compounding effect and reinvestment of returns.
In summary, the arithmetic average return is suitable for analyzing short-term performance, while the geometric average return is preferred evaluating long-term growth and the compounding effect of returns.
learn more about Average Return here:
https://brainly.com/question/29662426
#SPJ11
Explain why the set of natural numbers {1,2,3,4,...} and the set of even numbers {2, 4, 6, 8, . . .} of positive even numbers
Answers
The set of natural numbers {1,2,3,4,...} and the set of positive even numbers {2, 4, 6, 8, . . .} are different because natural numbers include all positive integers, while even numbers only include those that are divisible by 2 with no remainder.
About the setsTwo important sets of numbers are natural numbers and even numbers. The set of natural numbers consists of numbers that are not negative, beginning with 1 and continuing indefinitely with 2, 3, 4, and so on.
The set of even numbers, on the other hand, consists of numbers that are divisible by 2, beginning with 2, 4, 6, and so on.
Positive integers refer to natural numbers. Any integer greater than zero is a positive integer.
Zero is not a positive integer. Hence, the set of natural numbers consists of {1,2,3,4,…}
On the other hand, the set of even numbers consists of {2, 4, 6, 8, . . .}.
Therefore, {1,2,3,4,…} and {2, 4, 6, 8, . . .} are two different sets of numbers where one set is composed of positive integers (natural numbers) and the other is composed of positive even numbers.
Learn more about set in math at
https://brainly.com/question/30339736
#SPJ11
What is 2,520 divide 36
Answers
PLD HELP ME I WILL FAIL PLS

Answers
Answer:
you scammed me
Step-by-step explanation:
i ain't helping you give me my 50 points. fail for all I care you loser
sin^6 theta - cos^6 theta = ( 1-2cos^2 theta) (1- sin^2 theta .cos^2 theta )
Answers
Please find attached herewith the solution of your question.
if you have any question, feel free to ask.

Which shows two triangles that are congruent by ASA?
Answers
Answer:
A and D
Step-by-step explanation:
The two triangles that are congruent by ASA is discussed below.
What is Congruency?Two figures are said to be "congruent" if they can be positioned perfectly over one another. Both of the bread slices are the same size and shape when stacked one on top of the other. "Congruent" refers to things that are precisely the same size and shape.
Angle-Side-Angle refers to the ASA Congruence rule.
According to this rule, two triangles are said to be congruent if any two of their respective angles and the side that is included between them are equal to the corresponding angles and the included side of the other triangle.
For example, there are ABC and DEF in which ∠ B = ∠ E, ∠ C = ∠ F, and BC = EF
Then, the triangle that Δ ABC ≅ Δ DEF by ASA congruence rule.
Learn more about Congruency here:
https://brainly.com/question/7888063
#SPJ5
Given a polynomial and one of its factors, find the remaining factors of the polynomial.
x^3-9x^2+27x-27; x-3
Answers
The factors of the polynomial x^3-9x^2+27x-27 are (x -3), (x - 3) and (x - 3)
What is Factor of the PolynomialThe polynomial you provided is x^3-9x^2+27x-27. If you know one of the factors of this polynomial, we can use that to find the remaining factors.
One factor of this polynomial is (x-3) as it gives remainder zero when divided by (x-3)
quotient is x² - 6x + 9
remainder is zero
So the remaining factors are (x-3) and x² - 6x + 9
Alternatively, we can factor the remaining quadratic polynomial x² - 6x + 9
by using Factor theorem or by using difference of squares
x² - 6x + 9 = (x - 3)²
So the remaining factors are (x-3) and (x - 3)
So the original polynomial can be factored as (x-3)(x-3)(x-3) = (x-3)³
Learn more on factors of polynomial here;
https://brainly.com/question/25299657
#SPJ1
In triangle ABD, AC is a median. The value of AC is?

Answers
Step 1
A median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, thus bisecting that side.
Therefore,
\(\begin{gathered} Since\text{ C is the midpoint, }\bar{\text{DC}}\text{=}\bar{\text{CB}}\text{ } \\ 28=x+2 \\ x=28-2 \\ x=26 \end{gathered}\)Step 2
Find the value of Line AC the median.
\(\begin{gathered} \bar{AC}=x+8 \\ \bar{AC}=26+8=\text{ 34} \end{gathered}\)Hence, the value of line AC is 34
if the ratio is 434:7 whats the rate
Answers
Answer:
62
Step-by-step explanation:
The radius of circle S is half the radius of circle L. The radius of circle L is 8 millimeters.
Which measurement is closest to the area of circle S in square millimeters?
Answers
Area of the circle S be 16π square. millimeter
What is an area of circle ?
The area of a circle is the space the circle occupies in the two-dimensional plane. Alternatively, the space occupied within the boundary/circumference of a circle is called the area of the circle. The formula for the area of a circle is A = πr2, where r is the radius of the circle. A unit area is a unit square. Examples: m2, cm2, in2, etc. Circle area = π\(r^{2}\)in square units (Pi)π = 22/7 or 3.14. Pi (π) is the ratio of the circumference to the diameter of any circle. This is a special mathematical constant.
It is given that the radius of circle S is half the radius of circle L and the radius of circle L is 8 millimeters.
Radius of the circle S = 8/2 = 4 millimeters
Area of the circle S = π\(r^{2}\) = π\((4)^{2}\) = 16π square. millimeter
Therefore, area of the circle S be 16π square. millimeter
To learn more about the area of circle from the given link.
https://brainly.com/question/10645610
#SPJ1
many elementary school students in a school district currently have ear infections. a random sample of children in two different schools found that 11 of 40 at one school and 12 of 30 at the other have ear infections. at the 0.05 level of significance, is there sufficient evidence to support the claim that a difference exists between the proportions of students who have ear infections at the two schools?
Answers
Since the p-value is greater than the significance level of 0.05, we fail to reject the null hypothesis. Therefore, there is not sufficient evidence to support the claim that a difference exists between the proportions of students who have ear infections at the two schools.
To determine if there is sufficient evidence to support the claim that a difference exists between the proportions of students who have ear infections at the two schools, we can use a two-sample z-test for the difference in proportions.
The null hypothesis is that there is no difference between the proportions of students with ear infections at the two schools, while the alternative hypothesis is that there is a difference.
Let p1 be the proportion of students with ear infections at the first school and p2 be the proportion at the second school. The test statistic is given by:
z = (p1 - p2) / sqrt(p_hat * (1 - p_hat) * (1/n1 + 1/n2))
where p_hat is the pooled proportion, n1 and n2 are the sample sizes from the first and second schools, respectively.
The pooled proportion is given by:
p_hat = (x1 + x2) / (n1 + n2)
where x1 and x2 are the number of students with ear infections in each school.
Using the given data, we have:
n1 = 40, n2 = 30
x1 = 11, x2 = 12
p1 = x1/n1 = 11/40 = 0.275
p2 = x2/n2 = 12/30 = 0.4
p_hat = (x1 + x2) / (n1 + n2) = (11 + 12) / (40 + 30) = 0.355
The test statistic is:
z = (0.275 - 0.4) / sqrt(0.355 * 0.645 * (1/40 + 1/30)) = -1.197
Using a standard normal table or calculator, the p-value for a two-tailed test with a test statistic of -1.197 is approximately 0.231.
To know more about null hypothesis,
https://brainly.com/question/17157597
#SPJ11
Quis
bentuk pangkat dari
2² + 3² - 2²=
note:. user Indonesia
Answers
Answer:
9 Should be your answer
Step-by-step explanation:
\(2^{2}\) = 4
\(3^{2}\) = 9
These will help us as we solve this problem.
Then: 2² + 3² - 2²
= 4 + 9 - 4
= 9
Kind requests:
Please give brainliest :D
The distance between Lincoln, NE, and Boulder, CO, is about 500 miles. The distance between Boulder, CO, and a third city is 200 miles.
A map of the United notes.
Assuming the three cities make a triangle on the map, which values represent the possible distance, d, in miles, between Lincoln, NE, and the third city?
< d
Answers
The values that represent the possible distance, d, in miles, between Lincoln, NE, and the third city are given as follows:
300 < d < 699.
When does a set of three measurements can represent a triangle?A set of measurements can represent a triangle if the sum of the two smaller measurements is greater than the greater measures.
The measurements for this problem are given as follows:
500 miles.200 miles.x miles.Then if 500 miles is the largest distance, we have that:
x can be between 300 and 500.
If x is the largest distance, we have that:
x can be between 501 and 699.
Then the range of possible distances is given as follows:
300 < d < 699.
(which are the distances for each case).
More can be learned about set of measurements and triangles at brainly.com/question/24432457
#SPJ1
Answer:
see picture
Step-by-step explanation:

Determine if the relation is a function. In your handwritten work, explain why or why not.
Please and Thank you!!!

Answers
Answer:
Step-by-step explanation:
Its not a function. The reason its not a function is because it doesnt pass the vertical line test. You could graph these points physically or you could think about it. The domain is the x value, while the range is the allowed y values. So by having the same x value relate to two different y values, just makes no sense. Imagine the function is x+4 and we are given in that graph that when x equals 6, the y equals 9 and 10. That isnt possible because we know the answer is 10, not 9, it cant be both.
Another way you could prove this is by graphing. If you try to take the slope in that interval where 6 coorelates to two y values. The change in y is 1, but the change in x is 0. When you divide 1/0, your calculator blows up. Try it
Find the mean of the following data set. 42, 45, 58, 63 1. 42 2. 47 3. 52
Answers
Answer:
52
Step-by-step explanation:
42, 45, 58, 63
The mean is the sum divided by the number of terms
(42+ 45+ 58+ 63)/4
208/4
52
Answer:
Step-by-step explanation:
42 + 45 + 58 +631 + 422 + 473 + 52 = 1723
then divide by 7 to get 246.142857
hope this helps :)
A Group of drivers were looking at their debts. Mike is in $250.00 of debt. Sammy has $145.00 of debt. Guy has a positive bank balance of $300.00. Joe has a positive bank balance of $350.00. Who has the most money?
Answers
Answer:
Joe has the most money
Step-by-step explanation:
Mike has a balance of -250
Gammy has a balance of -145
Guy has a balance of +300
Joe has a balance of +350
Compare using >, <, or =
4/4 1/4
Answers
Answer:
\( \frac{4}{4} > \frac{1}{4} \)
Step-by-step explanation:
1 is bigger than a quarter.
Brandon invested $7,900 in an account paying an interest rate of 6\tfrac{1}{8}6 8 1 % compounded daily. Jacob invested $7,900 in an account paying an interest rate of 6\tfrac{5}{8}6 8 5 % compounded monthly. After 15 years, how much more money would Jacob have in his account than Brandon, to the nearest dollar?
Answers
Using the properties of compound interest we can calculate that Jacob will have $1485 more than Brandon in his account.
Brandon invested $7,900 at the rate of 6 1/8% compounded daily.
Principal = $7900
Time = 15 years
Rate = 6 1/8% = 49/8 %
Amount earned after n years:
\(A=P (1+\frac{r}{n})^{nt}\)
Now we will use these values to find the amount at the end of 15 years.
P = 7900
r = 0.06625
n = 365
t = 15
\(A=P (1+\frac{.06125}{365})^{15\times 365}\)
or, A = 19797.104...
or, A ≈ 19797.1
Again, Jacob invested the same sum at compound interest monthly at
6 5/8% .
Amount earned after 15 years:
P = 7900
r = 6.125
n = 12
t = 15
\(A=P (1+\frac{.06625}{12})^{15\times 12}\)
or, A = 21282.383..
or, A ≈ 21282.38
Amount earned by Jacob more than Brandon
= $21282.38 - $19797.1
= $148785.283..
≈ $1485
Hence Jacob will have $1485 more than Brandon in his account.
To learn more about compound interest visit:
https://brainly.com/question/13155407
#SPJ1
Which of the following is a geometric sequence?A. -5,0,10,25,45B. 1,2,4,8,16C.-3,1,5,9D. 4,8,24,96,480
Answers
Solution:
We are required to determine which is a geometric sequence.
Firstly, let us look at what a Geometric sequence is .
In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of non-zero numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio.
In summary, a Geometric sequence has a common ratio.
Let us take a look at the options one after the other
A. -5,0,10,25,45
\(\begin{gathered} \frac{0}{5}\text{ = 0} \\ \\ \frac{10}{0}=\infty \\ there\text{ is no common ratio here, hence it is not a Geometric sequence} \end{gathered}\)B. 1,2,4,8,16
\(\begin{gathered} \frac{2}{1}=2 \\ \\ \frac{4}{2}=2 \\ \\ \frac{8}{4}=2 \\ \\ \frac{16}{8}=2 \\ We\text{ can see that this sequence has a common ratio of 2, hence it is a geometric sequence} \end{gathered}\)C.-3,1,5,9
\(\begin{gathered} \frac{1}{-3}=-\frac{1}{3} \\ \\ \frac{5}{1}=5 \\ There\text{ is no common ratio here, hence it is not a geometric sequence} \end{gathered}\)D. 4,8,24,96,480
\(\begin{gathered} \frac{8}{4}=2 \\ \frac{24}{8}=3 \\ There\text{ is no common ratio here, hence it is not a geometric sequence} \end{gathered}\)Thus, the answer is B. 1,2,4,8,16
cindy baught 1/4 amount of ribbon and jacob baught 7/8 amount of ribbon how much ribbon does jacob have
Answers
Answer:
0.875
Step-by-step explanation:
For this graph, mark the statements that are true.
w+
+2
-2
-+
+1
-3
A. The range is the set of all real
numbers greater than or equal to
zero.
B. The domain is the set of all real
numbers.
C. The range is the set of all real
numbers.
D. The domain is the set of all real numbers greater than or equal to
zero.
SUDVAUT
Answers
The correct statements regarding the domain and the range of the function in this problem are given as follows:
B. The domain is the set of all real numbers.
C. The range is the set of all real numbers.
How to obtain the domain and range of a function?The domain of a function is defined as the set containing all the values assumed by the independent variable x of the function, which are also all the input values assumed by the function.The range of a function is defined as the set containing all the values assumed by the dependent variable y of the function, which are also all the output values assumed by the function.The function in this problem is defined for all real values, and assumes all real values, hence options B and C are the correct options for this problem.
Learn more about domain and range at https://brainly.com/question/26098895
#SPJ1

1. -3(2x - 8)= -12
2. 4(6 +2x)= 0
3. 3x +2x +6 = 15
4. 4= -2(x +3)
Answers
The solution of the expressions are,
1) x = 6
2) x = - 3
3) x = 9/5
4) x = - 5
What is an expression?Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
Given that;
All the expressions are,
1. -3(2x - 8)= -12
2. 4(6 +2x)= 0
3. 3x +2x +6 = 15
4. 4= -2(x +3)
Now,
Since, All the expressions are,
1. -3(2x - 8)= -12
2. 4(6 +2x)= 0
3. 3x +2x +6 = 15
4. 4= -2(x +3)
Solve as;
1. -3(2x - 8) = -12
⇒ - 3 × 2x - 3 × - 8 = - 12
⇒ - 6x + 24 = - 12
⇒ 24 + 12 = 6x
⇒ 6x = 36
⇒ x = 6
2. 4(6 +2x) = 0
⇒ 4 × 6 + 4 × 2x = 0
⇒ 24 + 8x = 0
⇒ 8x = - 24
⇒ x= - 3
3. 3x +2x +6 = 15
⇒ 5x + 6 = 15
⇒ 5x = 15 - 6
⇒ 5x = 9
⇒ x = 9/5
4. 4 = -2(x +3)
⇒ 4 = - 2x - 6
⇒ 2x = - 6 - 4
⇒ 2x = - 10
⇒ x = - 5
Thus, All the solution of the expressions are,
1) x = 6
2) x = - 3
3) x = 9/5
4) x = - 5
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ1
A bicycle repair shop offers two service packages to its customers: a tune up or a complete overhaul, which includes the tune up plus some additional services. All bicycles go through wheel balancing before leaving the shop. The repair shop is open 60 hours per week and receives an average of 180 bicycles each week. The shop employs three "tune up" technicians, one "additional services" technician, and two wheel balancing" specialists. Past data indicates that 25% of customers opt for the "additional services" option. Wheel Tune Up Balancing T = 75 T= 20 minutes minutes Additional Services T = 72 minutes a) Create a demand matrix for this process b) What will be the daily capacity at each stage of the process? c) Find the implied utilizations for each stage of the process. d) What will be the weekly capacity of the process? e) Is the flow rate of this process capacity-constrained or demand-constrained?
Answers
A bicycle repair shop that offers two service packages: a tune-up and a complete overhaul.
The shop operates for 60 hours per week and receives an average of 180 bicycles each week. To analyze the capacity and utilization of the process, we need to consider the time taken at each stage and the demand for each service option. We'll break down the problem into multiple parts and provide a detailed explanation using mathematical terms.
a) Creating the Demand Matrix:
To create a demand matrix, we need to determine the number of bicycles going through each stage of the process. Let's denote the demand for tune-up as T and the demand for additional services as A.
Given that the average number of bicycles received per week is 180 and 25% of customers opt for additional services, we can calculate the demands as follows:
Demand for tune-up (T) = Total demand - Demand for additional services
T = 180 - (0.25 * 180)
T = 180 - 45
T = 135
Demand for additional services (A) = 0.25 * Total demand
A = 0.25 * 180
A = 45
Now, we can create a demand matrix based on the demand for each service option:
Demand Matrix:
Tune-up Additional Services Wheel Balancing
Tune-up [135 0 0]
Additional [0 45 0]
Services
Total [ 135 45 0 ]
The demand matrix shows the number of bicycles flowing through each stage of the process.
b) Daily Capacity at Each Stage:
To calculate the daily capacity at each stage, we need to consider the time taken for each service option. Given that the shop operates for 60 hours per week, we can calculate the daily capacity at each stage:
Tune-up technician time per bicycle (\(T_{tuneup}\)) = 75 minutes
Additional services technician time per bicycle (\(T_{additional}\)) = 72 minutes
Wheel balancing specialist time per bicycle (\(T_{balancing}\)) = 20 minutes
Daily Capacity (C) = (60 hours * 60 minutes) / (\(T_{tuneup}\) + \(T_{additional}\) + \(T_{balancing}\))
Substituting the given values:
C = (60 * 60) / (75 + 72 + 20)
C = 21600 / 167
C ≈ 129.34 bicycles per day
Therefore, the daily capacity at each stage of the process is as follows:
Tune-up: 129 bicycles per day
Additional Services: 129 bicycles per day
Wheel Balancing: 129 bicycles per day
c) Implied Utilizations:
To find the implied utilizations, we need to compare the demand and the capacity at each stage of the process. Utilization can be calculated as the demand divided by the capacity.
Implied Utilization (U) = Demand / Daily Capacity
For the Tune-up stage:
\(U_{tuneup}\) = 135 / 129 ≈ 1.05
For the Additional Services stage:
\(U_{additional}\) = 45 / 129 ≈ 0.35
For the Wheel Balancing stage:
\(U_{balancing}\) = 0 / 129 = 0
The implied utilizations show how efficiently each stage of the process is being utilized. Utilization values greater than 1 indicate that the stage is operating beyond its capacity.
d) Weekly Capacity of the Process:
To calculate the weekly capacity of the process, we multiply the daily capacity by the number of days the shop is open per week:
Weekly Capacity = Daily Capacity * Number of days shop is open per week
Given that the shop is open for 60 hours per week, the number of days the shop is open per week can be calculated as follows:
Number of days shop is open per week = 60 hours / 24 hours per day = 2.5 days
Therefore, the weekly capacity of the process is:
Weekly Capacity = Daily Capacity * Number of days shop is open per week
Weekly Capacity = 129 bicycles per day * 2.5 days
Weekly Capacity = 322.5 bicycles per week
e) Flow Rate and Constraint Analysis:
To determine if the flow rate of the process is capacity-constrained or demand-constrained, we compare the weekly capacity to the demand for each service option.
Demand for Tune-up (\(T_{demand}\)) = 135 bicycles per week
Demand for Additional Services (\(A_{demand}\)) = 45 bicycles per week
Comparing the demands with the weekly capacity:
\(T_{demand}\) < Weekly Capacity (135 < 322.5)
\(A_{demand}\) < Weekly Capacity (45 < 322.5)
Since both the demands for tune-up and additional services are less than the weekly capacity, the flow rate of the process is demand-constrained. This means the shop has the capacity to handle the current demand without operating beyond its limits.
To know more about Demand Matrix here
https://brainly.com/question/13012912
#SPJ4
8 _ 6 _ 4 _ 2=6 you can use - ,+, x
Answers
Answer:
\(+, -, \times\)
Step-by-step explanation:
This is one of those questions where trial and error are used.
Trying out different combos until I get the right answer:
\(8-6+4\times2=10\)
\(8+6-4\times2=6\)
Nice! The correct answer is \(+, -, \times\)
Can someone help with this
The measure of angle B = 31 degrees, measure of angle C
= 121 degrees, and b = 9. Then a =
to the
nearest tenth.
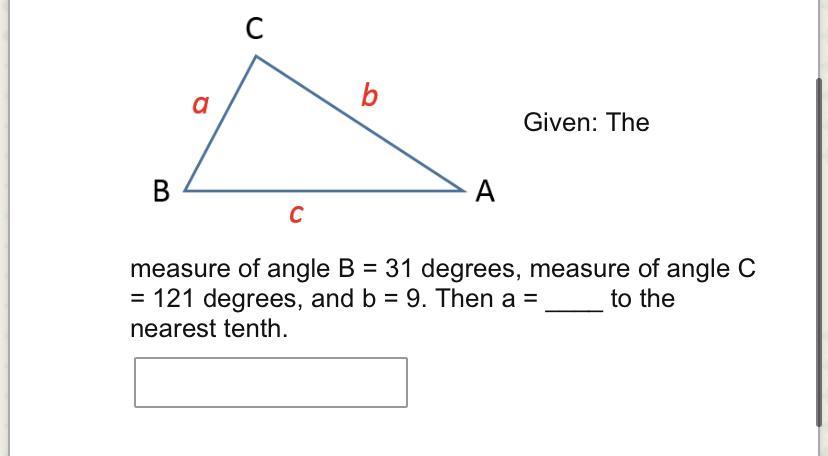
Answers
side a= 8.2
side c = 15
angle A = 28