A store salesperson is paid 3% of his sales as a commission. He made sales of $2500. How much was his commission?
Answers
1) Write 3% as 3/100
2) Since, finding the fraction of a number is same as multiplying the fraction with the number, we have:
\(\frac{3}{100}\) of 2500 = \(\frac{3}{100}\) × 2500
Therefore, the answer is 75
If you are using a calculator, simply enter 3÷100×2500 which will give you 75 as the answer.
Commission = $75
Related Questions
If the price of a particular chocolate bar is increased by 20%, and it used to be $2, what is the new price after the increase?
Answers
To find this, you can multiply the original price ($2) by 1.20, which represents the 20% increase.
$2 x 1.20 = $2.40
So the chocolate bar now costs $2.40 after the 20% increase.
How do you write 3.50 x 102 in standard form?
Answers
A student is attempting to convert a slope-intercept equation into standard form. Which of the following statements best applies to the sample math given below? Given y=1/4x+2 I first isolate the constant. After doing so, I get the equation -1/4x+y=2 To remove the fraction, I multiply by –4, giving the equation x-4y=2 which is the final answer. A. the work shown to isolate the constant is not correct B. the work shown to remove all fractions is not correct C. the final answer is not in standard form D. the work shown is correct
Answers
The statement that applies to the sample math is:
B. the work shown to remove all fractions is not correct
How to change the subject of the formula?The given steps are:
y = ¹/₄x + 2
- I first isolate the constant.
- After doing so, I get the equation: -¹/₄x + y = 2
- To remove the fraction, I multiply by –4, giving the equation x - 4y=2, which is the final answer.
The correct steps are as follows:
y = ¹/₄x + 2
First isolate the constant to get: y - ¹/₄x = 2
To remove the fraction, Multiply the obtained equation by –4
So, Equation : x - 4y = -8
On comparing both the work we can see that in the given work the removal of fraction is done incorrectly
They didn't multiply -4 on the right hand side .
Thus, option B applies.
Read more on subject of formula at: https://brainly.com/question/657646
#SPJ1
(100 POINTS!!!) The polynomial function
M(t)= 0.5t^4 + 3.45t^3 -96.65t^2 +347.7t
can be used to estimate the number of milligrams of the pain relief medication ibuprofen in the bloodstream t hours after 400 mg of the medication has been taken. Find the number of milligrams of ibuprofen in the bloodstream at t = 0, 1, 2, and so on, up to 6 hr.
Round the function values to the nearest tenth.
Then Use the function values you found in the previous question to sketch a graph of the function.
Answers
Answer:
See attached
Step-by-step explanation:
\(M(t)= 0.5t^4 + 3.45t^3 -96.65t^2 +347.7t\)
for t = 0, 1, 2, 3, 4, 5 and 6
\(M(0)= 0.5(0^4) + 3.45(0^3) -96.65(0^2) +347.7(0) = 0\\\\M(1)= 0.5(1^4) + 3.45(1^3) -96.65(1^2) +347.7(1) =255\\\\M(2) = 0.5(2^4) + 3.45(2^3) -96.65(2^2) +347.7(2)=344.4\\\\M(3)= 0.5(3^4) + 3.45(3^3) -96.65(3^2) +347.7(3) =306.9\\\\M(4)= 0.5(4^4) + 3.45(4^3) -96.65(4^2) +347.7(4)=193.2\\\\M(5)= 0.5(5^4) + 3.45(5^3) -96.65(5^2) +347.7(5)=66\\\\M(6)= 0.5(6^4) + 3.45(6^3) -96.65(6^2) +347.7(6)=0\\\)
Plotting M(t) against t we will get the graph


Answer:
\(\begin{array}{c|c}t&M(t)\\\cline{1-2} 0&0\\1&255\\2&344.4\\3&306.9\\4&193.2\\5&66\\6&0\end{array}\)
See attached for the graph of the function.
Step-by-step explanation:
Given polynomial function:
\(M(t)= 0.5t^4 + 3.45t^3 -96.65t^2 +347.7t\)
The given polynomial function can be used to estimate the number of milligrams of the pain relief medication ibuprofen in the bloodstream t hours after 400 mg of the medication has been taken.
To find the number of milligrams of ibuprofen in the bloodstream at different time points, substitute the given values of t into the given function M(t).
\(\begin{aligned}t=0 \implies M(0)&= 0.5(0)^4 + 3.45(0)^3 -96.65(0)^2 +347.7(0)\\&=0+0+0+0\\&=0\; \sf mg\end{aligned}\)
\(\begin{aligned}t=1 \implies M(1)&= 0.5(1)^4 + 3.45(1)^3 -96.65(1)^2 +347.7(1)\\&=0.5(1)+ 3.45(1) -96.65(1) +347.7(1)\\&=0.5 + 3.45 -96.65 +347.7\\&=255\; \sf mg\end{aligned}\)
\(\begin{aligned}t=2 \implies M(2)&= 0.5(2)^4 + 3.45(2)^3 -96.65(2)^2 +347.7(2)\\&= 0.5(16) + 3.45(8) -96.65(4) +347.7(2)\\&=8+27.6-386.6+695.4\\&=344.4\; \sf mg\end{aligned}\)
\(\begin{aligned}t=3 \implies M(3)&= 0.5(3)^4 + 3.45(3)^3 -96.65(3)^2 +347.7(3)\\&= 0.5(81) + 3.45(27) -96.65(9) +347.7(3)\\&=40.5+93.15-869.85+1043.1\\&=306.9 \; \sf mg\end{aligned}\)
\(\begin{aligned}t=4 \implies M(4)&= 0.5(4)^4 + 3.45(4)^3 -96.65(4)^2 +347.7(4)\\&= 0.5(256) + 3.45(64) -96.65(16) +347.7(4)\\&=128+220.8-1546.4+1390.8\\&=193.2\; \sf mg\end{aligned}\)
\(\begin{aligned}t=5 \implies M(5)&= 0.5(5)^4 + 3.45(5)^3 -96.65(5)^2 +347.7(5)\\&= 0.5(625) + 3.45(125) -96.65(25) +347.7(5)\\&=312.5+431.25-2416.25+1738.5\\&=66\; \sf mg\end{aligned}\)
\(\begin{aligned}t=6 \implies M(6)&= 0.5(6)^4 + 3.45(6)^3 -96.65(6)^2 +347.7(6)\\&= 0.5(1296) + 3.45(216) -96.65(36) +347.7(6)\\&=648+745.2-3479.4+2086.2\\&=0\; \sf mg\end{aligned}\)
To sketch a graph of the function, plot these values on a graph with time on the x-axis and ibuprofen concentration on the y-axis, and draw a smooth curve through the plotted points. An appropriate scale to use is x-axis : y-axis = 1 : 50.

HELP ASAP I WILL GIVE 30 points to whoever can show their work!

Answers
Answer:
Step-by-step explanation:
sin(A)=2/5
\(cos^2(A) +sin^2(A)=1\\cos^2(A)+[\frac{2}{5}]^2=1\\cos^2(A)+\frac{4}{25}=1\\ cos^2(A)=1-\frac{4}{25}\\ cos^2(A)=\frac{21}{25}\\ cosA=\frac{\sqrt{21} }{5}\)
2
1
-1
-2
Determine the period.
2 4
6 8 10 12 14
Acellus

Answers
According to the information we can infer that the period of the graph is 8.
How to determine the period of the graph?To determine the period of the graph we have to consider that the period of a grah is the distance between rigdes. So, in this case we have to count what is the difference between each rigde.
In this case, the distance between rigdes is 8 units because the first is located in the line 1 an the second is located in the line 9. So we can conclude that the period of the graph is 8.
Learn more about period in: https://brainly.com/question/23532583
#SPJ1
Which inequality represents the situation described below?
The distance, d, is less than 200 miles.
A. d ≥ 200
B. d > 200
C. d ≤ 200
D. d < 200
Answers
Hello!
The distance, d, is less than 200 miles.
B. d > 200
25/23 to the nearest hundred
Answers
Answer:
1.09 is the answer for the question
Answer:
1.09
Step-by-step explanation:
25/23 to the nearest hundred is mean to round up the decimal points.
25/23= 1.08695652174.
1.08695652174 to the nearest hundred would be 1.09.
Please give the brainliest! :D
The table shows the hourly wages (in dollars) of employees after they have worked at a company for x years. Use the linear regression feature
on a graphing calculator to find an equation of the line of best fit for the data. Round each value in your equation to the nearest hundredth.
Then use your equation to estimate the hourly wage of an employee who has worked at the company for 12 years.
Years, x Hourly wage (dollars per hour), y
1
$8.75
5
$10.50
3
$9.25
7
$11.25
The line of best fit is y =
The aproxímate hourly wage of a person who has worked at the company for 12 years is $___ per hour
Answers
Answer:
y= 0.5x + 8.2
$13.6 per hour
Step-by-step explanation:
(Is it weird that I had the same exact question? Maybe not. But I also found another person with the same question as me. It was a different question though. This is probably too late. But I'm just gonna try to answer it for anyone who needs it.
"Linear regression" is just a fancy word for scatter plots. Scatter plots take place in graphs. The dots or plots are scattered and the way they are scattered means something. If it's going down, it's negative, up it's positive, and if it's scattered, it has no corrolation.
Also, you should have learned this in 9th grade. So, check your notes.
If you don't have it, WRITE IT!!!
To find it in your calculator:
1. Go to "Lists and Spreadsheets"
2. Rename the first column "x" and the second on "y"
3. Write all of your numbers in the right column
1, 5, 3, 7 under the "x"
8.67, 10.50, 9.58, 11.41 under the "y"
4. Move your cursor to an empty cell
4. Click: "MENU" #4 #1 #3
5. Rename the correct rows "x" and "y" and press enter
6. Now you can find "m" and "b"
7. Then move your cursor to an empty cell and click "doc" "insert" #7
8. Find the x-axis and find "x"
9. Find the y-axis and find "y"
10. Now press "MENU" #4 #6 #1
And you found your y=mx+b: y=0.5x+8.2
Now, how much money per hour.
So you've found your m and b but now you have to:
1. Replace y with 15 and solve it
15=0.5x+8.2
-8.2 -8.2
6.8=0.5x
Divide 0.5 on both sides
6.8/0.5=13.6
13.6=x
$13.6 per hour
Determine how many integer solutions there are to
x₁ + x₂ + x3 + x₁ = 20, if
0≤x₁ < 3, 0≤ x₂ < 4, 0≤x3 <5, 0≤x4 < 6
Answers
Based on the information given, there are a total of 118 solutions.
How many possible solutions are there?This is a problem of solving a Diophantine equation subject to some conditions. Let's introduce a new variable y4 = 20 - (x1 + x2 + x3 + x4). Then the problem can be restated as finding the number of solutions to:
x1 + x2 + x3 + y4 = 20
Subject to the following conditions:
0 ≤ x1 < 3
0 ≤ x2 < 4
0 ≤ x3 < 5
0 ≤ y4 < 6
We can solve this problem using the technique of generating functions. The generating function for each variable is:
(1 + x + x^2) for x1
(1 + x + x^2 + x^3) for x2
(1 + x + x^2 + x^3 + x^4) for x3
(1 + x + x^2 + x^3 + x^4 + x^5) for y4
The generating function for the equation is the product of the generating functions for each variable:
(1 + x + x^2)^3 (1 + x + x^2 + x^3 + x^4 + x^5)
We need to find the coefficient of x^20 in this generating function. We can use a computer algebra system or a spreadsheet program to expand the product and extract the coefficient. The result is: 1118
Learn more about solutions in https://brainly.com/question/30665317
#SPJ1
Answer: This problem involves finding the number of non-negative integer solutions to the equation x₁ + x₂ + x3 + x₁ = 20 subject to the given constraints. We can use the stars and bars method to solve this problem.
Suppose we have 20 stars representing the sum x₁ + x₂ + x3 + x₁. To separate these stars into four groups corresponding to x₁, x₂, x₃, and x₄, we need to place three bars. For example, if we have 20 stars and 3 bars arranged as follows:
**|**||
then the corresponding values of x₁, x₂, x₃, and x₄ are 2, 4, 6, and 8, respectively. Notice that the position of the bars determines the values of x₁, x₂, x₃, and x₄.
In general, the number of ways to place k identical objects (stars) into n distinct groups (corresponding to x₁, x₂, ..., xₙ-₁) using n-1 separators (bars) is given by the binomial coefficient (k+n-1) choose (n-1), which is denoted by C(k+n-1, n-1).
Thus, the number of non-negative integer solutions to the equation x₁ + x₂ + x3 + x₁ = 20 subject to the given constraints is:
C(20+4-1, 4-1) = C(23, 3) = 1771
However, this count includes solutions that violate the upper bounds on x₁, x₂, x₃, and x₄. To eliminate these solutions, we need to use the principle of inclusion-exclusion.
Let Aᵢ be the set of non-negative integer solutions to the equation x₁ + x₂ + x3 + x₁ = 20 subject to the given constraints, where xᵢ ≥ mᵢ for some integer mᵢ. Then, we want to find the cardinality of the set:
A = A₀ ∩ A₁ ∩ A₂ ∩ A₃
where A₀ is the set of all non-negative integer solutions to the equation x₁ + x₂ + x3 + x₁ = 20, and Aᵢ is the set of solutions that violate the upper bound on xᵢ.
To find the cardinality of A₀, we use the formula above and obtain:
C(20+4-1, 4-1) = 1771
To find the cardinality of Aᵢ, we subtract the number of solutions that violate the upper bound on xᵢ from the total count. For example, to find the cardinality of A₁, we subtract the number of solutions where x₂ ≥ 4 from the total count. To count the number of solutions where x₂ ≥ 4, we fix x₂ = 4 and then count the number of solutions to the equation x₁ + 4 + x₃ + x₄ = 20 subject to the constraints 0 ≤ x₁ < 3, 0 ≤ x₃ < 5, and 0 ≤ x₄ < 6. This count is given by:
C(20-4+3-1, 3-1) = C(18, 2) = 153
Similarly, we can find the cardinalities of A₂ and A₃ by fixing x₃ = 5 and x₄ = 6, respectively. Using the principle of inclusion-exclusion, we obtain:
|A| = |A₀| - |A
Step-by-step explanation:
I'LL MARK THE BRAINLIEST
The diameter of a circle is 10 3/4 inches.
What is the radius, r, of the circle?
Enter your answer as a mixed number in simplest form by filling in the boxes.
Answers
Answer: The radius of the circle is 5 3/8 inches.
Step-by-step explanation:
The radius of the circle is half of the diameter. We can start by converting the mixed number diameter to an improper fraction:
10 3/4 = (10 × 4 + 3)/4 = 43/4
So, the diameter of the circle is 43/4 inches. The radius is half of this, which we can find by dividing by 2:
r = (43/4) ÷ 2 = 43/8
To simplify the fraction, we can divide the numerator and denominator by their greatest common factor (GCF), which is 1:
r = 43/8 = 5 3/8
Therefore, the radius of the circle is 5 3/8 inches.
Answer:5 3/4
Step-by-step explanation:
10 3/4 * 1/2
1/2 * 43/4 = 43/8
8/43=5 3/4
Solve the Simulataneous equations 2x + 4y=1
Answers
2 x + 4 y = 1 has the simultaneous equation \(x=\frac{1-4 y}{2}\) .Eliminate a variable by using the elimination procedure.
What do you meant by Simulataneous equations?for x, solve, \(2 x+4 y=1 \quad: \quad x=\frac{1-4 y}{2}\)
2 x + 4 y=1
4 y in the correct direction
2 x = 1 - 4 y
multiply both sides by two.
\(\frac{2 x}{2}=\frac{1}{2}-\frac{4 y}{2}\)
Simplify
\(x=\frac{1-4 y}{2}\)
You can find answers to both unknowns in two separate equations that have the same two unknowns in each. The three most popular approaches to solving are addition/subtraction, substitution, and graphing. simultaneous problems Equations: Elimination, Substitution, Graphical, and Matrix Methods | Vivax Solutions.
Steps for Solving Multiple Equations at Once Using the Elimination Method. Selecting a variable to remove is step one. Find the LCM of the variable's coefficients in step two. Step 3: Multiply the equations' two sides to create the coefficient of the variable you want to remove from the LCM.
To learn more about Simulataneous equations refer to :
https://brainly.com/question/148035
#SPJ1
The solution of the equation 3x + 4 =1 is a) 1 b) 0 c) -1 d) 2
Answers
Hello!
3x + 4 = 1
3x + 4 - 4 = 1 - 4
3x = -3
3x/3 = -3/3
x = -1
The solution of the equation 3x + 4 = 1 is -1.
The answer is:
C) x = -1
Work/explanation:
To solve this equation, I subtract 4 from each side:
\(\sf{3x+4=1}\)
Subtract :
\(\sf{3x=-3}\)
Divide each side by 3:
\(\sf{x=-1}\)
Hence, C is correct.
Find Matrix mixed questions

Answers
The only matrix that is certainly symmetric is a)\((a^2 - b^2).\)
We know that a matrix A is symmetric if it is equal to its transpose, that is \(A = A^T.\)
a) \((a^2 - b^2)\)
We can write the transpose of this matrix as
\((a^2 - b^2)^T = (a^2)^T - (b^2)^T = a^2 - b^2\), which is equal to the original matrix. Therefore, this matrix is symmetric.
b) (A+B)(A-B)
Expanding this expression, we get \((A+B)(A-B) = A^2 - AB + BA - B^2.\)
Taking the transpose of this, we get \((A^2)^T - (AB)^T + (BA)^T - (B^2)^T = A^2 - BA + AB - B^2.\)
Since AB and BA may not be equal, we cannot say for certain that this matrix is symmetric.
c) ABA
Taking the transpose of this matrix, we get\((ABA)^T = A^T B^T A^T\). Since \(A^T and B^T\) may not commute, we cannot say for certain that this matrix is symmetric.
d) ABAB
Taking the transpose of this matrix, we get \((ABAB)^T = B^T A^T B^T A^T\). Again, since \(A^T and B^T\) may not commute, we cannot say for certain that this matrix is symmetric.
Therefore, the only matrix that is certainly symmetric is a) \((a^2 - b^2).\)
for such more question on matrix
https://brainly.com/question/25581637
#SPJ11
the measurement of an angle is 40 in the length of a line segment is 80 cm the number of unique rhombuses that can be constructed using this information is
Answers
A rhombus is a quadrilateral whose 4 sides are equal, it means all have the same length
Once given the length of one of the sides, all sides have the same length. As we also know one of the angles of this rhombus, we are limited to construct one unique rhombus.
The answer is that only one rhombus can be constructed using this information.
What is 4 divided by 37.4??
Answers
Answer:
.101265823
Step-by-step explanation:
When x= 1, then y=
Just how ?

Answers
Which statement best describes the area of Triangle ABC shown below?
A triangle ABC is shown on a grid. The vertex A is on ordered pair 4 and 5, vertex B is on ordered pair 5 and 2, and the vertex C is on ordered pair 3 and 2.
(5 points)
Group of answer choices
It is twice the area of a rectangle with sides 2 units × 3 units.
It is one-half the area of a rectangle with sides 2 units × 3 units.
It is twice the area of a square of side length 3 units.
It is one-half the area of a square of side length 3 units.

Answers
Answer: It is one-half the area of a rectangle with sides 2 units × 3 units.
It is twice the area of a square of side length 3 units.
It is one-half the area of a square of side length 3 units.
Step-by-step explanation:
Answer:
It is one-half the area of a rectangle with sides 2 units × 3 units.
Step-by-step explanation:
because the base of the triangle is connected in the "quadrilateral way" the base is one-half the rectangle and the units are 2x3 so therefore that answer is the correct one.
a) (10 pts) Re-express the given differential equation as a first order differential equation by utilizing matrix
and vector notation and in accordance with ()
= () form.
b) (10 pts) Is the system obtained in (a) stable, neutrally stable of unstable? Determine this using matrix.
c) (10 pts) Compute the eigenvalues and eigenvectors of matrix.
d) (10 pts) Using the results computed in (c) find and matrices and show that =
−
relationship
(i.e., the diagonalization relationship) is a valid relationship.

Answers
a) To re-express the given differential equation as a first-order differential equation using matrix and vector notation, we can rewrite it in the form:
\(x' = Ax\)
where x is a vector and A is a square matrix.
b) To determine the stability of the system obtained in part (a), we need to analyze the eigenvalues of matrix A.
If all eigenvalues have negative real parts, the system is stable.
If at least one eigenvalue has a zero real part, the system is neutrally stable.
If at least one eigenvalue has a positive real part, the system is unstable.
c) To compute the eigenvalues and eigenvectors of matrix A, we solve the characteristic equation
\(det(A - \lambda I) = 0\),
where λ is the eigenvalue and I is the identity matrix.
By solving this equation, we obtain the eigenvalues.
Substituting each eigenvalue into the equation
\((A - \lambda I)v = 0\),
where v is the eigenvector, we can solve for the eigenvectors.
d) Once we have computed the eigenvalues and eigenvectors of matrix A, we can construct the diagonalization relationship as follows:
\(A = PDP^{(-1)}\)
where P is a matrix whose columns are the eigenvectors of A, and D is a diagonal matrix whose diagonal elements are the eigenvalues of A.
To show that this relationship is valid, we can compute \(PDP^{(-1)}\) and verify that it equals A.
For such more questions on differential equation
https://brainly.com/question/18760518
#SPJ8
Write (x - 5)(x + 5)(2x - 1) in standard form.
-x2 + 2x2 - 50x + 25
2r? - x? - 50x + 25
2x - x2 - 50x
-50x - x? + 2x
Answers
Answer:
2x3 - x2 - 50x + 25
Step-by-step explanation:
So the first thing you would do is multiply (x - 5)(x + 5)
x2 + 5x - 5x - 25
then you would simplify
x2 - 25
then you would multiply it by 2x - 1
(x2 - 25)(2x - 1)
2x3 - x2 - 50x + 25
so your answer is
2x3 - x2 - 50x + 25
27. What is the reflection image of (5, –3) across the y-axis? (–5, 3) (–5, –3) (–3, 5) (5, 3)
Answers
The search results are unrelated to the question of finding the reflection image of (5, -3) across the y-axis. To find the reflection image of a point across the y-axis, we need to change the sign of the x-coordinate of the point. Therefore, the reflection image of (5, -3) across the y-axis is (-5, -3).
The side of a triangle are in the ratio 4:4:3 what kind of triangle is it (b) calculate the smallest angle of the triangle to the nearest degree
Answers
The smallest angle of the equilateral triangle is 60 degrees
If the sides of a triangle are in the ratio 4:4:3, it implies that the lengths of the sides are proportional.
To determine the type of triangle, we examine the side lengths. Since all three sides are equal in length, we have an equilateral triangle.
For an equilateral triangle, all angles are equal. To calculate the smallest angle, we divide the total sum of angles in a triangle (180 degrees) by the number of angles, which is 3:
Smallest angle \(= \frac{180}{3} = 60\)\) degrees.
Therefore, the smallest angle of the equilateral triangle is 60 degrees (to the nearest degree).
For more questions on equilateral triangle:
https://brainly.com/question/17264112
#SPJ8
Will give brainlist PLEASE HELP ASAP!!!! If it says college math, that's false.
The graph below represents the money collected at the skating rink on Friday. Find the domain when the maximum number of people allowed in the skating rink is 75 people.
A=0 ≤ x ≤ 75
B= 20 ≤ y ≤ 320
C= 0 ≤ y ≤ 75
D= 20 ≤ x ≤ 320

Answers
Answer:
A is correct.
0 < x < 75 represents the correct domain.
I need help solving this

Answers
The cylinder has a volume of 150.796 in³. The cylinder has a surface area of 175.929 in².
What's volume of cylinder ?The quantity of three-dimensional space that an object or closed surface occupies is referred to as volume in mathematics. The cubic units of volume are m³, cm³, in³, and so on.
How does surface area work?The sum of all of an object's faces is its surface area in three dimensions. Wrapping, painting, and finally building things to achieve the best possible design are examples of real-world applications of the concept of surface areas.
Evaluating :Given that a volume of cylinder = h × r² × π
h = 12 in
r = 2 in
volume = ?
Volume of cylinder = h × r² ×π
= =12 × 3.14×(2)²
=37.68 × 4
=150.796 in³
B). Surface area of cylinder= 2πr² + 2πrh
=2× 3.14 × (2)²+2× 3.14× 2×12
=175.929in²
The formula V=r²(h) can be used to determine a cylinder's volume. Simply multiplying the area of the circular base shape by the height is all that is required to determine a cylinder's volume.
Learn more about Volume of cylinder :
brainly.com/question/24055431
#SPJ1
Following are financial statement numbers and ratios for Salsa Incorporated for the year ended December 31, Year 1 (in millions).NOPAT $584.5 NOA $3,5321Net operating profit margin (NOPM) 15.9%Net operating asset turnover (NOAT). 1.04 If we expected revenue growth of 5% in the next year, what would projected revenue be for the year ended December 31, Year 2? Select one: a. None of these are correctb. $3,532.1 million C. $3,492.3 million d. $3,859.9 million e. $3,673.4 million
Answers
The projected revenue for the year ended December 31, Year 2 is $3,673.4 million.
How to find Revenue?
The amount of gross income generated by sales of goods or services is referred to as revenue (or sales revenue) in various contexts. Revenue can be calculated simply by multiplying the quantity of sales by the average service price or sales price:
Revenue = Sales x Average Price of Service or Sales Price
To find the projected revenue for the year ended December 31, Year 2, we can use the following formula:
Projected revenue = Current revenue * (1 + Expected revenue growth)
In this case, the current revenue is equal to the NOA, which is $3,532.1 million. The expected revenue growth is 5%, so the projected revenue is:
$3,532.1 million * (1 + 0.05) = $3,673.4 million
Therefore, The projected revenue for the year ended December 31, Year 2 is $3,673.4 million.
To know more about Revenue visit,
https://brainly.com/question/16232387
#SPJ4
Find the values of x and y

Answers
Answer:
x = 90
y = 44
is the answer for the question
A markdown, or discount, is an example of a percent increase. Answer TRUE or FALSE.
True
O False
Answers
Answer:
true
Step-by-step explanation:
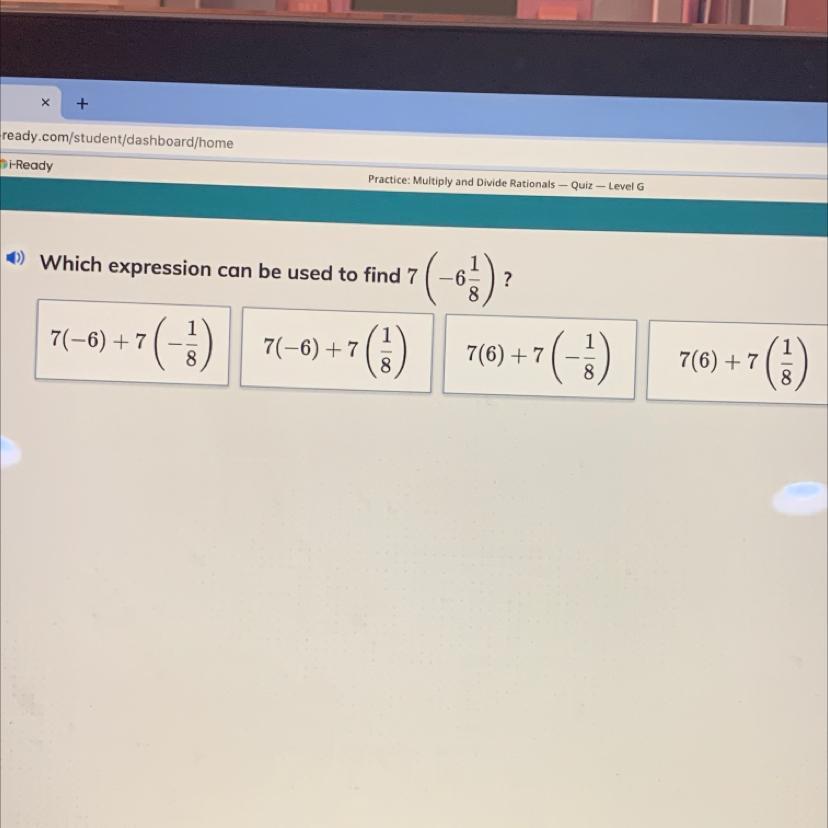
Which expression can be used to find 7
-6
?
7(-6) +7
7(-6) +7
7(6) + 7
7(6) + 7
()
Answers
-42 7/8
Explanation- Got it right
hope it helps !
Answer:
-42/7
Step-by-step explanation:
A lock has a 3-number code made up of 15 numbers. If none of the numbers are allowed to repeat, how many different ways can you choose three different numbers in order for a unique code?
Answers
Answer:2730
Step-by-step explanation:

The number of ways we can choose three different numbers in order for a unique code for this case is 2730
How many ways k things out of m different things (m ≥ k) can be chosen if order of the chosen things doesn't matter?We can use combinations for this case,
Total number of distinguishable things is m.
Out of those m things, k things are to be chosen such that their order doesn't matter.
This can be done in total of \(^mC_k = \dfrac{m!}{k! \times (m-k)!}\) ways.
If the order matters, then each of those choice of k distinct items would be permuted k! times.
So, total number of choices in that case would be:
\(^mP_k = k! \times ^mC_k = k! \times \dfrac{m!}{k! \times (m-k)!} = \dfrac{m!}{ (m-k)!}\\\\^mP_k = \dfrac{m!}{ (m-k)!}\)
This is called permutation of k items chosen out of m items (all distinct).
Given that:
The considered lock as a 3 number codeThere are 15 numbers available.None of the number can repeat.In a lock, the order of the way numbers are arranged matters.
Because of no repetition allowed, we can simulate this situation as:
The number of ways we can choose 3 numbers out of 15 numbers with order = The number of different ways we can choose three different numbers in order for a unique code.
And we have:
The number of ways we can choose 3 numbers out of 15 numbers with order = \(^{15}P_3 = \dfrac{15!}{(15-3)!} = \dfrac{15 \times 14 \times 13 \times 12!}{12!} = 2730\)
Thus, the number of ways we can choose three different numbers in order for a unique code for this case is 2730
Learn more about combinations and permutations here:
https://brainly.com/question/16107928
#SPJ2
The weight of an organ in adult males has a billship distribution with a mean of 330 g and a standard deviation of 50 g
Answers
Using the Empirical Rule, it is found that 99.7% of the weights are between 180 g and 480 g.
What does the Empirical Rule state?It states that, for a normally distributed random variable:
Approximately 68% of the measures are within 1 standard deviation of the mean.Approximately 95% of the measures are within 2 standard deviations of the mean.Approximately 99.7% of the measures are within 3 standard deviations of the mean.Hence, the bounds of the interval containing 99.7% of the weights is given by:
330 - 3 x 50 = 180 g.330 + 3 x 50 = 480 g.More can be learned about the Empirical Rule at https://brainly.com/question/24537145
#SPJ1