a store is having a 10%off sale it gives 10%off if the item is still ubove 100$ after the first discount if the jacket is 199.99 will you get the second discount? if so how much money will you save in total
Answers
Answer: $38 is the amount saved
To get second discount, 90% of the price must be > $100
hence 90% of 199.99 = 199.99/100*90 = $179.991 (Price after 1st discount)
Since the price after first discount is > $100 , it is eligible for second discount.
Price after 2nd discount of 10% = 179.991/100*90 = $161.9919
Savings = 199.99-161.9919 = 37.9981 = 38 dollars saved.
Step-by-step explanation:
199.99 * 0.9 = 179.99
179.99 * 0.9 = 161.99
199.99 - 161.99 = $38 amount saved
Related Questions
Can y’all solve this please

Answers
Consider the system dx/dt =4x−2y , dy/dt =x+ y
a) Compute the eigenvalues
b) For each eigenvalue, compute the associated eigenvectors.
c) Using HPGSystemSolver, sketch the direction field for the system,and plot the straightline solutions(if there are any). Plot the phase portrait.
Answers
The eigenvalues for the given system dx/dt = 4x - 2y, dy/dt = x + y are λ1 = 3 and λ2 = 2.
The associated eigenvectors are v1 = (1, 1) and v2 = (-1, 2). Using HPGSystemSolver, you can sketch the direction field, plot straight line solutions, and create the phase portrait.
To find the eigenvalues:
1. Write the system as a matrix: A = [[4, -2], [1, 1]]
2. Calculate the characteristic equation: det(A - λI) = 0, which gives (4 - λ)(1 - λ) - (-2)(1) = 0
3. Solve for λ, yielding λ1 = 3 and λ2 = 2
For eigenvectors:
1. For λ1 = 3, solve (A - 3I)v1 = 0, resulting in v1 = (1, 1)
2. For λ2 = 2, solve (A - 2I)v2 = 0, resulting in v2 = (-1, 2)
Using HPGSystemSolver or similar software, input the given system to sketch the direction field, plot straight line solutions (if any), and generate the phase portrait. This visual representation helps in understanding the system's behavior.
To know more about eigenvectors click on below link:
https://brainly.com/question/31391960#
#SPJ11
ASAP I NEED ANSWERS PLEASE
Select the correct answer:
What is the equation of the parabola shown with its focus on this graphp
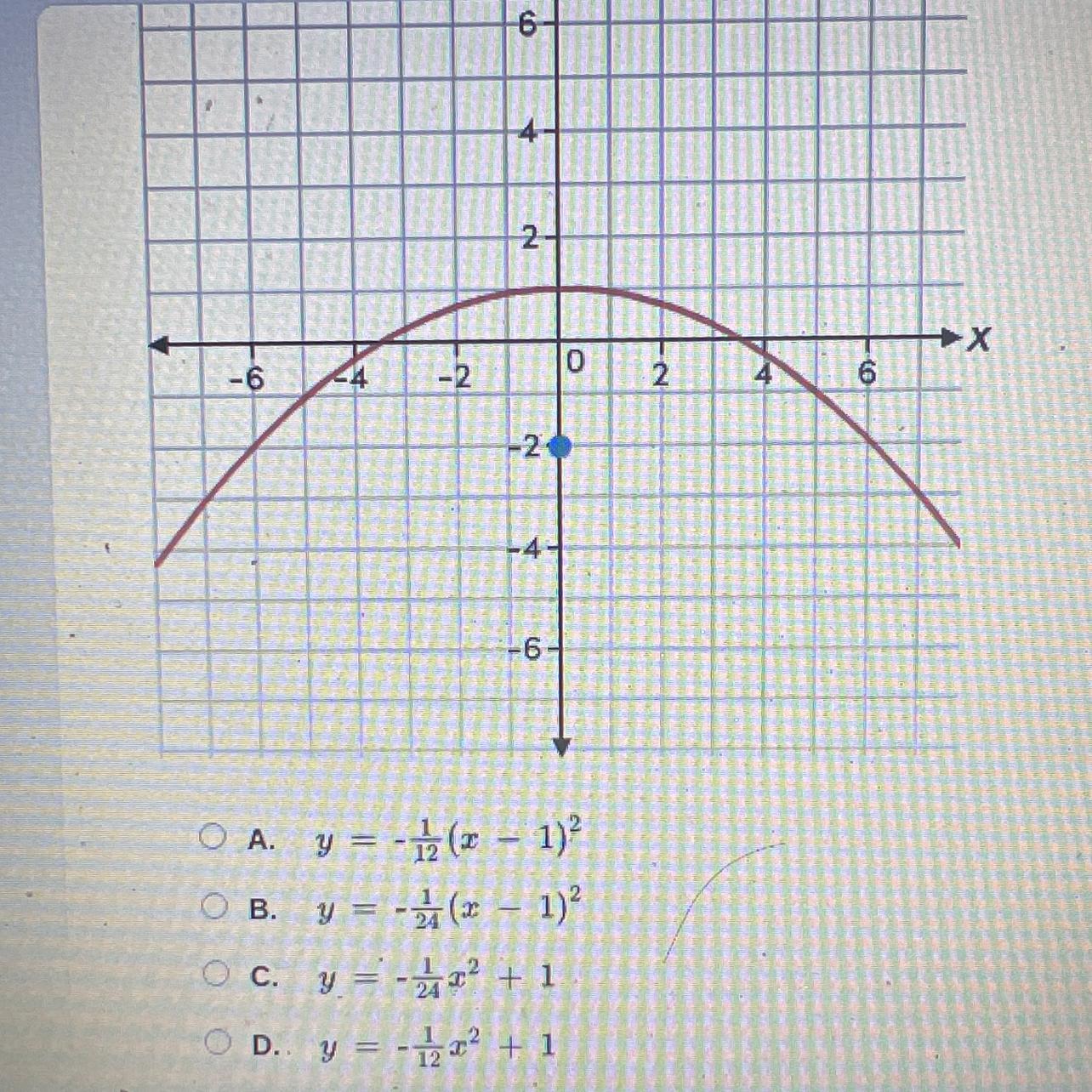
Answers
The equation of the parabola shown with its focus on this graph is D. y = \(-\frac{1}{12} \text x^2\) + 1.
What is a parabola?A parabola is a mirror-symmetrical, roughly U-shaped plane curve that is used in mathematics. It corresponds to a number of mathematical explanations that appear to differ on the surface but which all define the same curves.
A line and a point (the focus) are two ways to describe a parabola (the directrix). Not the directrix is the main focus. The location of points in that plane that are equally spaced apart from the directrix and the focus is known as the parabola.
Conic sections, which are formed when a right circular conical surface and a plane perpendicular to another plane that is tangential to the conical surface intersect, are another way to describe parabolas.
Learn more about parabola
https://brainly.com/question/21685473
#SPJ1
PLZ HELP ILL MARK YOU BRAINLEST ‼️
a) 120°
b) 50°
c) 70°
d) 180°

Answers
Answer:
120°
Step-by-step explanation:
Add the 2 opposite angles to find the exterior angle.
50° + 70° = 120°
If my answer is incorrect, pls correct me!
If you like my answer and explanation, mark me as brainliest!
-Chetan K
Write the equation of the line fully simplified slope-intercept form.

Answers
Answer:
y = -3x + 7
Step-by-step explanation:
I see points (0, 7) and (1, 4).
slope = m = (4 - 7)/(1 - 0) = -3
y-intercept = 7
y = mx + b
y = -3x + 7
Check all fractions equivalent to 2⁄8.
Check all that are true.
1⁄2
1⁄6
4⁄16
1⁄4
4⁄12
Answers
Select the correct answer from the drop-down menu.
Triangle ABC is shown with angle A measuring 45 degrees, angle B measuring 90 degrees, and angle C measuring 45 degrees.
In this triangle, the product of tan A and tan C is
.
Answers
In this triangle, the product of tan A and tan C is `(BC)^2/(AB)^2`.
The given triangle ABC has angle A measuring 45 degrees, angle B measuring 90 degrees, and angle C measuring 45 degrees , Answer: `(BC)^2/(AB)^2`.
We have to find the product of tan A and tan C.
In triangle ABC, tan A and tan C are equal as the opposite and adjacent sides of angles A and C are the same.
So, we have, tan A = tan C
Therefore, the product of tan A and tan C will be equal to (tan A)^2 or (tan C)^2.
Using the formula of tan: tan A = opposite/adjacent=BC/A Band, tan C = opposite/adjacent=AB/BC.
Thus, tan A = BC/AB tan C = AB/BC Taking the ratio of these two equations, we have: tan A/tan C = BC/AB ÷ AB/BC Tan A * tan C = BC^2/AB^2So, the product of tan A and tan C is equal to `(BC)^2/(AB)^2`.
Answer: `(BC)^2/(AB)^2`.
For more questions on adjacent sides, click on:
https://brainly.com/question/28394984
#SPJ8
a 12 inch thin‑crust cheese pizza is cut equally into eight slices. assuming a uniform distribution of sauce and toppings,
Answers
If there were any variations in the distribution during the preparation process, the slices might have slight differences in the amount of sauce and toppings.
each slice of the 12-inch thin-crust cheese pizza would have an equal distribution of sauce and toppings. This means that each slice would have the same amount of sauce and toppings spread evenly across its surface.
Since the pizza is cut equally into eight slices, each slice would represent 1/8th of the total pizza. Therefore, each slice would have an equal portion of the sauce and toppings.
It's important to note that the exact amount of sauce and toppings on each slice would depend on the original distribution applied to the pizza before it was sliced. If the pizza was prepared with a uniform distribution of sauce and toppings across the entire pizza, then each slice would indeed have an equal amount. However, if there were any variations in the distribution during the preparation process, the slices might have slight differences in the amount of sauce and toppings.
Learn more about exact amount here:
https://brainly.com/question/30069661
#SPJ11
What is the difference between a discrete
probability distribution and a continuous
probability distribution?
Give your own example of each. What is the
expected value, and what does it measure?
How is it computed for a discrete probability
distribution?
Answers
A discrete probability distribution is a statistical distribution that relates to a set of outcomes that can take on a countable number of values, whereas a continuous probability distribution is one that can take on any value within a given range.Therefore, the main difference between the two types of distributions is the type of outcomes that they apply to.
An example of a discrete probability distribution is the probability of getting a particular number when a dice is rolled. The possible outcomes are only the numbers one through six, and each outcome has an equal probability of 1/6. Another example is the probability of getting a certain number of heads when a coin is flipped several times.
On the other hand, an example of a continuous probability distribution is the distribution of heights of students in a school. Here, the range of heights is continuous, and it can take on any value within a given range.
The expected value of a probability distribution measures the central tendency or average of the distribution. In other words, it is the long-term average of the outcome that would be observed if the experiment was repeated many times.
For a discrete probability distribution, the expected value is computed by multiplying each outcome by its probability and then adding the results. In mathematical terms, this can be written as E(x) = Σ(xP(x)), where E(x) is the expected value, x is the possible outcome, and P(x) is the probability of that outcome.
For example, consider the probability distribution of the number of heads when a coin is flipped three times. The possible outcomes are 0, 1, 2, and 3 heads, with probabilities of 1/8, 3/8, 3/8, and 1/8, respectively. The expected value can be computed as E(x) = (0*1/8) + (1*3/8) + (2*3/8) + (3*1/8) = 1.5.
Therefore, the expected value of the distribution is 1.5, which means that if the experiment of flipping a coin three times is repeated many times, the long-term average number of heads observed will be 1.5.
Problem 2. Smasher Van bound for Koronadal City leaves Polomolok every 15 minutes
while Nustafa Van leaves every 20 minutes.
5. How often do the two vans leave Polomolok at the same time
a. every 30 minutes
c. every 1 hour
b. every 40 minutes
d. every 2 hours
6. How many times will the Smasher Van leave Polomolok so that the two von leave
together
a. 2 times b. 3 times c. 4 times d. 5 times
7. How many times will the Nustafa Van leave Polomolok so that the two vons leave
together
a. 2 times b. 3 times c. 4 times d. 5 times
Answers
Answer:
5. c. Every 1 hour
6. c. 4 times
7. b. 3 times
Step-by-step explanation:
The given parameters of the rate of departure of the two vans are;
The rate of departure of Smasher Van bound for Koronadal City = Every 15 minutes
The rate of departure of Nustafa Van= Every 20 minutes
5. The time, 'x', when the two vans leave at the same time is given by the Lowest Common Multiple (LCM) of 15 and 20 as follows;
Multiples of 15 = 15, 30, 45, 60
Multiples of 20 = 20, 40, 60
Therefore, the LCM of 15 and 20 = 60
The time, when the two vans leave at the same time = Every 60 minutes = Every 1 hour
The time, when the two vans leave at the same time = Every 1 hour
6. The number of times the Smasher Van leaves Polomolok so that the two vans leave together is given by the number of multiples 15 minutes in 60 minutes = 60 minutes/(15 minutes) = 4 times
7. The number of times the Nustafa Van leaves Polomolok so that the two vans leave together is given by the number of multiples 20 minutes in 60 minutes = 60 minutes/(20 minutes) = 3 times.
5. c. Every 1 hour
6. c. 4 times
7. b. 3 times
Let's solve it one by one:
The given parameters of the rate of departure of the two vans are;
The rate of departure of Smasher Van bound for Koronadal City = Every 15 minutes
The rate of departure of Nustafa Van= Every 20 minutes
5. The time, 'x', when the two vans leave at the same time is given by the Least Common Multiple (LCM) of 15 and 20 as follows;
Multiples of 15 = 15, 30, 45, 60
Multiples of 20 = 20, 40, 60
Therefore, the LCM of 15 and 20 = 60
The time, when the two vans leave at the same time = Every 60 minutes = Every 1 hour
The time, when the two vans leave at the same time = Every 1 hour
6. The number of times the Smasher Van leaves Polomolok so that the two vans leave together is given by the number of multiples 15 minutes in 60 minutes = \(\frac{60}{15}=4\text{times}\)
7. The number of times the Nustafa Van leaves Polomolok so that the two vans leave together is given by the number of multiples 20 minutes in 60 minutes = \(\frac{60}{30}=3\text{times}\)
Learn more:
brainly.com/question/18369259
an automobile speedometer with circular scales reading both miles per hour and kilometers per hour is shown. what speed is indicated in kilometers per hour?
Answers
The
speed
indicated in kilometers per hour is 85 km/h, as shown on the circular scale of the automobile
speedometer
.
The automobile
speedometer
is an instrument that measures the speed of a vehicle. It has a circular
scale
that reads both miles per hour (mph) and kilometers per hour (km/h). To determine the
speed
in kilometers per hour, the user must first locate the needle on the scale. The needle should be pointing to a specific number that corresponds to both mph and km/h. For example, if the needle is pointing to 85, then the speed indicated in kilometers per hour is 85 km/h. It is important to note that if the needle is located between two
numbers
, the user should determine the approximate speed by interpolating the two numbers. To find the speed in miles per hour, the user can simply look at the number that corresponds to the needle on the scale. In this case, the speed indicated in miles per hour is 53 mph.
The complete question: An automobile speedometer with circular scales reading both miles per hour and kilometers por hour is shown. What speed is indicated in miles per hour? 100 120 140 80 160 *60 180 200 40 20 220 Own 240 Express your answer in miles per hour v.2 mph
Learn more
speedometer
here
https://brainly.com/question/463709
#SPJ4
What is the value of the expression 24 + 10•8?
Answers
Answer:
\(\large\boxed{\text{The expression is equal to 104}}\)
Step-by-step explanation:
\(24+10 \cdot 8 \\24+80\\104\)
\((2x3)²- 7\)
Answers
Answer:
4x⁶ - 7
Step-by-step explanation:
\( \sf{( {2x}^{3} )}^{2} - 7\)
\( \sf( {2}^{2} \times {x}^{3 \times 2} ) - 7\)
\( \sf {4x}^{6} - 7\)
If integral from negative 2 to 3 of the quantity 2 times f of x plus 2 end quantity dx equals 18 and integral from 1 to negative 2 of f of x dx equals negative 10 comma then integral from 1 to 3 of f of x dx is equal to which of the following? a 4b 0c −6d −8
Answers
For an integral value of \(I_1 = \int_{ -2}^{3} [2f(x) + 2] dx = 18 \\ \) and
\(I_2 = \int_{ 1}^{-2} f(x)dx = -10 \\ \), the computed value of integral \(\int_{ 1}^{3} f(x)dx\) is equals to the -6. So, option(c) is right one.
In mathematics, an integral is the continuous process of a sum, which is used to calculate areas, volumes, and their properties. Integration is a way to sum up parts to the whole.
We have an integral say \(I_1 = \int_{ -2}^{3} [2f(x) + 2] dx = 18 \\ \)
\(I_2 = \int_{ 1}^{-2} f(x)dx = 10 \\ \)
We have to determine value of \(\int_{ 1}^{3} f(x)dx\).
Using the properties of integral, consider integral \(I_1 = \int_{ -2}^{3} [2f(x) + 2] dx = 18\\ \)
from distribution property, \(I_1 = \int_{ -2}^{3} 2f(x) dx + \int_{ -2}^{3} 2 dx = 18 \\ \)
\(2 \int_{ -2}^{3} f(x) dx + [ 2x]_{ -2}^{3} = 18\)
\(2 \int_{ -2}^{3} f(x) dx + 10 = 18\)
\(2 \int_{ -2}^{3} f(x) dx = 8\)
\(\int_{ -2}^{3} f(x) dx = 4\)
Now, consider the required integral and rewrite, \(\int_{ 1}^{3} f(x)dx = \int_{ 1}^{-2} f(x)dx + \int_{ -2}^{3} f(x)dx \\ \)
Substitute all known values of integrals
\(\int_{ 1}^{3} f(x)dx = 10 + 4 = 14 \)
Hence, required value is 14.
For more information about integral, visit:
https://brainly.com/question/27419605
#SPJ4
Krista pilots a drone from her house to the park. The relative locations are shown in the coordinate plane. What is the distance the drone flies?
The drone flies ___ kilometers.

Answers
Answer:
The distance the drone flies is 4 units or 8 kilometers.
If the points be park: (-1,-2) and home: (3,1)then, the distance of the drone flies is 10 km.
What is distance?
The length along a line or line segment between two coordinates on the line or line segment.
The distance between the points (a, b) and (c, d) exists given by \($\sqrt{(a-c)^{2}+(b-d)^{2}}$\).
In three dimensional space, the distance between the points (a, b, c) and (d, e, f) exists \($\sqrt{(a-d)^{2}+(b-e)^{2}+(c-f)^{2}}$\).
Given:
park: (-1,-2) and home: (3,1)
Distance = \($\sqrt{(a-c)^{2}+(b-d)^{2}}$\)
\($&\Rightarrow \sqrt{(-2-1)^{2}+(-1-3)^{2}} \times 2 \\\)
= 10 km
Therefore, the distance the drone flies is 10 km.
To learn more about distance
https://brainly.com/question/1872885
#SPJ2
(BRAINLIEST) HELP ASAP!

Answers
Answer:
1380
Step-by-step explanation:
60(15) = 900
2280 - 900 = 1,380

You are the director of the customer service center in Company Alpha. You find that the mean time between calls to the center is 6 minutes with standard deviation of 4 minutes. The effective response time is 11 minutes with a standard deviation of 20 minutes. (a) Identify the following parameters: ta
tθ
∂a
∂θ
ra:
rθ:
Answers
The identified parameters are:
ta = 6 minutes
tθ = 11 minutes
∂a = 4 minutes
∂θ = 20 minutes
ra = 1/6 minutes^(-1)
rθ = 1/11 minutes^(-1)
ta: Mean time between calls to the center
tθ: Effective response time
∂a: Standard deviation of the time between calls to the center
∂θ: Standard deviation of the effective response time
ra: Rate of calls to the center (inverse of ta, i.e., ra = 1/ta)
rθ: Rate of effective response (inverse of tθ, i.e., rθ = 1/tθ)
Given information:
Mean time between calls to the center (ta) = 6 minutes
Standard deviation of time between calls (∂a) = 4 minutes
Effective response time (tθ) = 11 minutes
Standard deviation of effective response time (∂θ) = 20 minutes
Using this information, we can determine the values of the parameters:
ta = 6 minutes
tθ = 11 minutes
∂a = 4 minutes
∂θ = 20 minutes
ra = 1/ta = 1/6 minutes^(-1)
rθ = 1/tθ = 1/11 minutes^(-1)
So, the identified parameters are:
ta = 6 minutes
tθ = 11 minutes
∂a = 4 minutes
∂θ = 20 minutes
ra = 1/6 minutes^(-1)
rθ = 1/11 minutes^(-1)
Learn more about Standard Deviation here:
https://brainly.in/question/50665860
#SPJ11
If trapezoid
EFGH is
reflected over
the x-axis, what
will be the
coordinates of
the new image?

Answers
Answer:
e (2,-1)
f (4,-1)
g (5,-4)
h (1,-4)
On average, a gym claims that 85% of its members renew their memberships every year. If the gym has 400 members, predict how many will renew their membership. Is the gym’s claim accurate if 330 members renew their memberships? Explain.
Answers
Answer:
340 people would renew their membership if the gym had 400 members
The gym's claim is not accurate, because the prediction should be 340 people instead of 330
Step-by-step explanation:
With 400 members, we can predict how many will renew their membership by multiplying 400 by 0.85:
400(0.85)
= 340
So, this would predict that 340 people would renew their membership.
The gym's claim that 330 members would renew their memberships is not accurate, because the correct prediction should be 340 people.
Part B
Notice that two line segments are formed on each transversal between the central parallel line and the outer parallel
lines. Measure the lengths of the four line segments.

Answers
ANSWER. Part b
Line segment PM = 2.2 length
ML = 2.2
ON = 2
NK = 2

Answer:60
Step-by-step explanation:
Please help my work is almost due and I have no clue

Answers
Answer:
4 = x
Step-by-step explanation:
64 = x^3
Take the cube root of each side
64^ (1/3) = x^3 ^ (1/3)
4 = x
What is the orthogonality assumption in ordinary least squares (OLS), taking LaTeX: Y\:=a+bX as the model, and the error term is LaTeX: \epsilon?
Answers
The orthogonality assumption in ordinary least squares (OLS) regression states that the error term (ε) is uncorrelated with the independent variable (X).
In OLS regression, the model assumes that the relationship between the dependent variable (Y) and the independent variable (X) can be represented as Y = a + bX + ε, where ε is the error term.
The orthogonality assumption states that this error term is uncorrelated with X, meaning that there is no systematic relationship between the independent variable and the random error. In other words, the error term represents the variation in Y that cannot be explained by X.
The orthogonality assumption is crucial because it allows OLS to estimate the coefficients (a and b) in a way that is unbiased and efficient. If there were a correlation between X and the error term, it would imply that the variation in Y not explained by X is related to X, leading to biased and inefficient coefficient estimates. By assuming orthogonality, OLS can separate the effects of X on Y from the random error, allowing for reliable estimation of the relationship between the variables.
To learn more about coefficients click here:
brainly.com/question/1594145
#SPJ11
What is the length of an arc having an 17 inch radius and
included angle of 220 degrees? Give your answer rounded to two
decimal places.
Answers
The radius of the circle is 17 inches. The included angle is 220°.We are to find the length of the arc having a 17 inch radius and an included angle of 220 degrees.
Let's first find the circumference of the circle having a radius of 17 inches.Circumference of a circle is given by the formula;C=2πrSubstituting the given value of radius, r = 17 inches in the above equation, we get;
C=2πr
=2π(17)
= 34π inches
Now let's find the length of the arc that subtends the angle 220° on a circle whose radius is 17 inches.The formula for finding the length of the arc is given by;
L = θ/360° × 2πr
WhereL = length of the arc.θ = angle in degrees subtended by the arc. (i.e., 220° in our case)r = radius of the circle. (i.e., 17 inches in our case).Substituting the given values of the angle θ and radius r in the above equation, we get;
L = θ/360° × 2πr
=220/360° × 2π(17)
≈66.91 inches
Therefore, the length of the arc having a 17 inch radius and included angle of 220 degrees is approximately 66.91 inches (rounded to two decimal places).
For more information on Circumference visit:
brainly.com/question/28757341
#SPJ11
find the number of ways to select 3 pages in ascending index order
Answers
The number of ways to select 3 pages in ascending index order depends on the total number of pages available.
To find the number of ways to select 3 pages in ascending index order, we can use the concept of combinations . In combinatorics, selecting objects in a specific order is often referred to as permutations. However, since the order does not matter in this case, we need to consider combinations instead.
The number of ways to select 3 pages in ascending index order can be calculated using the combination formula. Since we are selecting from a set of pages, without replacement and order doesn't matter, we can use the formula C(n, k) = n! / (k! (n-k)!), where n is the total number of pages and k is the number of pages we want to select.
Learn more about combination formula here:
https://brainly.com/question/13090387
#SPJ11
Miss Hamel and Miss Nelli spent the same amount of money at Target on Black Friday. Miss Hamel bought an $88 bike to donate for the holiday season. She also bought 30 baby onesie outfits to donate. Miss Nellie bought
a PlayStation 5 game for $30 and 35 baby onesie outfits to donate. The cost of each onesie was the same for Miss Hamel and Miss Nelli. How much was the cost of each onesie?
please help ill give brainliest
Answers
Answer:
21
Step-by-step explanation:
Question 1: American ladybugs have an average adult length of 1 cm with a known standard deviation of 0.2 cm. The population of American ladybugs in Raleigh was around 440000 last spring. Assume a normal distribution for the lengths of adult American ladybugs. Your niece asks you what's the probability of a random ladybug in Raleigh being bigger than 1.5 cm. Is it appropriate to calculate this probability? Select one: a. No, because the population distribution is skewed. b. No, because the sample size is less than 30. c. No, because the empirical rule is violated. d. Yes. Clear my choice Question 2: Regardless of your answer to the previous question, calculate this probability using a normal distribution. Report your answer to four decimal places. Question 3: Calculate the probability of observing an average American ladybug length between 0.95 cm and 1.05 cm for a random sample of 20 ladybugs. Give your answer accurate to four decimal places. If you found assumptions to be violated in the previous question, answer this question as if the assumptions had not been violated.
Answers
Yes, it is appropriate to compute the likelihood that a random ladybug in Raleigh will be larger than 1.5 cm.
What is meant by standard normal distribution?With a mean of 0 and a standard deviation of 1, the standard normal distribution is a normal distribution. The standard deviation, which indicates how much a given measurement deviates from the mean, is given by the standard normal distribution, which has zero as its center.
As the sample size is sufficient (440000) and the standard deviation is known, it is appropriate to use a normal distribution to estimate the distribution of ladybug lengths. A 1.5 cm long ladybug's z-score can be calculated as follows:
z = (1.5 - 1) / 0.2 = 2.5
We can calculate the likelihood of a z-score being greater than 2.5 using a conventional normal distribution table to be roughly 0.0062. Hence, the likelihood that a random ladybug in Raleigh will be larger than 1.5 cm is around 0.0062 or 0.62%.
Therefore, the correct answer is option d. Yes. Clear my choice.
The complete question is;
American ladybugs have an average adult length of 1 cm with a known standard deviation of 0.2 cm. The population of American ladybugs in Raleigh was around 440000 last spring. Assume a normal distribution for the lengths of adult American ladybugs. Your niece asks you what's the probability of a random ladybug in Raleigh being bigger than 1.5 cm. Is it appropriate to calculate this probability? Select one:
a. No, because the population distribution is skewed.
b. No, because the sample size is less than 30.
c. No, because the empirical rule is violated.
d. Yes. Clear my choice
To learn more about standard normal distribution refer to:
https://brainly.com/question/13781953
#SPJ1
round to the nearest hundredths
683.004
Answers
Consider the following data drawn independently from normally distributed populations: (You may find it useful to appropriate table: z table or t table)
xˉ1 = −17.1
s1^2 = 8.4
n1=22
xˉ2 = −16.0
s2^2 = 8.7
n2 = 24
a. Construct the 90% confidence interval for the difference between the population means. Assume the population va unknown but equal. (Round final answers to 2 decimal places.)
confidence interval is __ to __
Answers
The 90% confidence interval for the difference in the population means is -2.51 to 0.31
Calculating the 90% confidence interval for the population mean differenceFrom the question, we have the following parameters that can be used in our computation:
xˉ₁ = −17.1
s₁² = 8.4
n₁ = 22
xˉ₂ = −16.0
s₂² = 8.7
n₂ = 24
Calculate the pooled variance using
P = (df₁ * s₁² + df₂ * s₂²)/df
Where
df₁ = 22 - 1 = 21
df₂ = 24 - 1 = 23
df = 22 + 24 - 2 = 44
So, we have
P = (21 * 8.4 + 23 * 8.7)/44
P = 8.56
Also, we have the standard error to be
SE = √(P/n₁ + P/n₂)
So, we have
SE = √(8.56/22 + 8.56/24)
SE = 0.86
The z score at 90% CI is 1.645, and the CI is calculated as
CI = (x₁ - x₂) ± z * SE
So, we have
CI = (-17.1 + 16.0) ± 1.645 * 0.86
This gives
CI = -1.1 ± 1.41
Expand and evaluate
CI = (-2.51, 0.31)
Hence, the confidence interval is -2.51 to 0.31
Read more about confidence interval at
https://brainly.com/question/15712887
#SPJ1
______ has at least one solution, and an inconsistent system has no solution.
Answers
The statement "Consistent system of equations has at least one solution, and an inconsistent system has no solution" is true.
In the context of systems of linear equations, a consistent system refers to a system where there exists at least one solution that satisfies all the equations in the system. This means that the equations can be simultaneously satisfied by a set of values for the variables.
On the other hand, an inconsistent system refers to a system of equations that has no solution. This occurs when the equations are contradictory or cannot be satisfied simultaneously by any values for the variables.
Therefore, a consistent system guarantees the existence of at least one solution, while an inconsistent system does not have any solution.
To know more about Consistent system refer here:
https://brainly.com/question/12791933
#SPJ11
Sixty-four percent of voters in a very large electorate support candidate Smith in an upcoming election. A student employee working the evening shift at a telephone survey facility calls voters at random and asks them which candidate they prefer. a. What is the probability that, among five voters the student calls, exactly one supports candidate Smith? b. What is the probability that, among five voters the student calls, at least one supports candidate Smith? c. What is the probability that the first voter supporting candidate Smith is reached on the fifth call, i.e., what is the probability that it takes the student five calls to reach the first voter who supports candidate Smith? d. What is the probability that the third voter supporting candidate Smith is reached on the fifth call, i.e., what is the probability that it takes the student five calls to reach three voters who supports candidate Smith?
Answers
The probabilities are calculated assuming independence of each call and that the success probability remains constant throughout the calls.
a. The probability that, among five voters the student calls, exactly one supports candidate Smith can be calculated using the binomial probability formula. With a success probability of 64% (0.64) and exactly one success (k = 1) out of five trials (n = 5), the probability can be calculated as follows:
\[
P(X = 1) = \binom{5}{1} \times (0.64)^1 \times (1 - 0.64)^4
\]
The calculation results in approximately 0.369, or 36.9%.
b. The probability that, among five voters the student calls, at least one supports candidate Smith can be calculated as the complement of the probability that none of the voters support Smith. Using the binomial probability formula, with a success probability of 64% (0.64) and no success (k = 0) out of five trials (n = 5), the probability can be calculated as follows:
\[
P(X \geq 1) = 1 - P(X = 0) = 1 - \binom{5}{0} \times (0.64)^0 \times (1 - 0.64)^5
\]
The calculation results in approximately 0.997, or 99.7%.
c. The probability that the first voter supporting candidate Smith is reached on the fifth call can be calculated as the probability of not reaching a Smith supporter in the first four calls (0.36) multiplied by the probability of reaching a Smith supporter on the fifth call (0.64):
\[
P(\text{{First Smith Supporter on Fifth Call}}) = (1 - 0.64)^4 \times 0.64
\]
The calculation results in approximately 0.014, or 1.4%.
d. The probability that the third voter supporting candidate Smith is reached on the fifth call can be calculated as the probability of reaching two Smith supporters in the first four calls (0.64 for the first call, 0.36 for the second call, and 0.36 for the third call) multiplied by the probability of reaching a Smith supporter on the fifth call (0.64):
\[
P(\text{{Third Smith Supporter on Fifth Call}}) = (0.64)^2 \times (1 - 0.64) \times 0.64
\]
The calculation results in approximately 0.147, or 14.7%.
know more about probabilities :brainly.com/question/29381779
#SPJ11
The probabilities are calculated assuming independence of each call and that the success probability remains constant throughout the calls. The calculation results in approximately 0.369, or 36.9%.
a. The probability that, among five voters the student calls, exactly one supports candidate Smith can be calculated using the binomial probability formula. With a success probability of 64% (0.64) and exactly one success (k = 1) out of five trials (n = 5), the probability can be calculated as follows:
[P(X = 1) = \binom{5}{1} \times (0.64)^1 \times (1 - 0.64)^4\]
The calculation results in approximately 0.369, or 36.9%.
b. The probability that, among five voters the student calls, at least one supports candidate Smith can be calculated as the complement of the probability that none of the voters support Smith. Using the binomial probability formula, with a success probability of 64% (0.64) and no success (k = 0) out of five trials (n = 5), the probability can be calculated as follows:
[P(X \geq 1) = 1 - P(X = 0) = 1 - \binom{5}{0} \times (0.64)^0 \times (1 - 0.64)^5\]
The calculation results in approximately 0.997, or 99.7%.
c. The probability that the first voter supporting candidate Smith is reached on the fifth call can be calculated as the probability of not reaching a Smith supporter in the first four calls (0.36) multiplied by the probability of reaching a Smith supporter on the fifth call (0.64):
\[
P(\text{{First Smith Supporter on Fifth Call}}) = (1 - 0.64)^4 \times 0.64
\]
The calculation results in approximately 0.014, or 1.4%.
d. The probability that the third voter supporting candidate Smith is reached on the fifth call can be calculated as the probability of reaching two Smith supporters in the first four calls (0.64 for the first call, 0.36 for the second call, and 0.36 for the third call) multiplied by the probability of reaching a Smith supporter on the fifth call (0.64):
\[
P(\text{{Third Smith Supporter on Fifth Call}}) = (0.64)^2 \times (1 - 0.64) \times 0.64
\]
The calculation results in approximately 0.147, or 14.7%.
know more about probabilities :brainly.com/question/29381779
#SPJ11