A sporting equipment company wants to sell a new bicycle helmet. They have developed a function, shown below, where total profit, p, can be determined based on sale price, s.
What will be the total profit if the sale price of the helmet is $60?
Answers
Answer:
\( p(s) = -24s^2 +2200 s -18000\)
If we use the valie of s =60 we have
\( p(60) = -24 (60)^2 +2200*60 -18000\)
And after solve we got:
\( p(60)= -86400 +132000 -18000 =27600\)
So then the best option for this case would be:
$27,600
Step-by-step explanation:
Using the following info in order to complete the problem:
p(s)=-24s^(2)+2200s-18000
$112,560
$27,600
$111,120
$236,400
$14,240
We have the following function given:
\( p(s) = -24s^2 +2200 s -18000\)
If we use the valie of s =60 we have
\( p(60) = -24 (60)^2 +2200*60 -18000\)
And after solve we got:
\( p(60)= -86400 +132000 -18000 =27600\)
So then the best option for this case would be:
$27,600
Related Questions
PLS HELP 3x+4 = 2 (x - 1)
Answers
Answer:
x= -6
Step-by-step explanation:
3x+4= 2 (x - 1)
3x+4= 2x -2
Subtract 4 from both sides of the equation
Simplify
Subtract 2x from both sides of the equation
Simplify
= -6
Answer:
x = -6
Step-by-step explanation:
I've attached a pic, hopefully it is clear and understandable:)

A line contains the points (-3, 2) and (0, 2). What is the equation of this
line in slope-intercept form?
A) y = 3x + 2
B) y=-3x + 2
C) y = -3
D) y = 2
Answers
Answer:
y = 0x + 2
Step-by-step explanation:
First, plug the values in the formula.
y2 - y1 / x2 - x1 2-2/ -3 - 0
= 0
Now find the y-intercept.
y = 0x + b
2 = 0 (-3) + b
2 = 0 + b
2 = b
Answer:
D
Step-by-step explanation:
I took the test
calculate the number in the middle of -7 and 6
Answers
Answer:
I believe 0.5 , if I'm reading this question right.
Step-by-step explanation:
-7, -6, -5, -4, -3, -2, -1, 0.5, 0, 1, 2, 3, 4, 5, 6
7 numbers on ⬆ 7 numbers on
left side. right side.
Please correct me if I'm wrong, and I hope this makes sense.
8^2-12 1/2 ÷ 3 = solve
Answers
Answer: 62
The expression given below
\(t^2\text{ - 12w / x}\)Where t = 8, w = 1/2 and x = 3
To find the value of this expression, we need to substitute the value of t, w and x into the above expression
\(\begin{gathered} t^2\text{ - 12w / x} \\ (8)^2\text{ - 12(}\frac{1}{2})\text{ / 3} \\ (8)^2\text{ - }\frac{12}{2}\text{ / 3} \\ =\text{ 64 - 6/3} \\ =\text{ 64 - 2} \\ =\text{ 62} \end{gathered}\)below is a scatterplot of the natural logarithm of weight vs. the natural logarithm of length. this relationship is clearly more linear that the one above. does this suggest that the relationship between length and weight can be modeled by an exponential function or by a power function? explain.
Answers
The relationship between length and weight can be modeled by a power function.
The fact that the scatterplot of the natural logarithm of weight vs. the natural logarithm of length shows a more linear relationship suggests that the relationship between length and weight can be better modeled by a power function rather than an exponential function. This is because when the logarithms of both variables are taken, an exponential function becomes a linear function, while a power function remains a non-linear function.
In a power function, one variable is raised to a power that is not necessarily an integer, whereas in an exponential function, one variable is raised to a constant power. Therefore, it is more likely that the relationship between length and weight can be modeled by a power function.
To know more about logarithms, here
brainly.com/question/24626259
#SPJ4

Find the solutions to the equation below.
Check all that apply.
6x² +5x-4 = 0
A. X = 1/2
B. x=-1/3
C. x= 1/3
D. x = -2
E. x = 4
F. x= -4/3
Answers
Answer: x=1/2, x=-4/3 ==> A and F
Step-by-step explanation:
6x² +5x-4 = 0
6x²-3x+8x-4 = 0
3x(2x-1)+4(2x-1) = 0
(3x+4)(2x-1)=0
3x+4=0
3x=-4
x=-4/3
2x-1=0
2x=1
x=1/2
x=1/2, x=-4/3 ==> A and F
given the nine-sided regular polygon $a 1a 2a 3a 4a 5a 6a 7a 8a 9$, how many distinct equilateral triangles in the plane of the polygon have at least two vertices in the set $\{a 1, a 2, \dots, a 9\}$?
Answers
The total number of distinct equilateral triangles in the plane of the polygon A₁, A₂,A₃,A₄,A₅,A₆,A₇,A₈,A₉ with at least two vertices in the set {A₁, A₂,......,A₉} is 84 x 9 = 756.
Given the nine-sided regular polygon A₁, A₂,A₃,A₄,A₅,A₆,A₇,A₈,A₉ the question is how many distinct equilateral triangles in the plane of the polygon have at least two vertices in the set {A₁, A₂,......,A₉}.
To answer this question, we must first consider the number of ways in which we can select three distinct points from the set. Since the set contains nine distinct points, we can select three distinct points from the set in Computing Binomial Coefficients C(n, r) where n is 9 and r is 3 . We get C(9, 3)=84
Now, we must consider the number of distinct equilateral triangles that can be formed in the plane of the polygon with at least two vertices in the set. Since the regular polygon A₁,A₂,A₃,A₄,A₅,A₆,A₇,A₈,A₉ has nine sides, there are nine distinct equilateral triangles that can be formed in the plane of the polygon with at least two vertices in the set.
Therefore, the total number of distinct equilateral triangles in the plane of the polygon A₁, A₂,A₃,A₄,A₅,A₆,A₇,A₈,A₉ with at least two vertices in the set {A₁, A₂,......,A₉} is 84 x 9 = 756.
Learn more about equilateral triangles at :https://brainly.com/question/3461022
#SPJ4
Can I get help please

Answers
The amount of money that I will have at the end of 20 years would be =$4,480. That is option D
What is compound interest?Compound interest is defined as the interest that is being earned on an account which is based on the rate and the time the investment was made.
The total amount invested (p)= $2,000
The rate of investment (r) = 5%
The time of investment(t)= 12 year
The compound interest warm from that account;
= P×T×R/100.
= 2,000×12×5/100
= 120000/100
= $1200
For the next 8 years with the rate of 8% ;
= 2,000×8×8/100
= 128000/100
= $1280
The total compound interest = $1200+$1280= $2,480
Therefore, the amount of money that I will have at the end of 10 years would be = 2000+2480 = $4,480
Learn more about simple interest here:
https://brainly.com/question/25793394
#SPJ1
are there differences in airfare depending on which travel agency website you utilize? the following data were collected on travel agency websites on july , . the following table contains the prices in u.s. dollars for a one-way ticket between the cities listed on the left for each of the three travel agency websites. here the pairs of cities are the blocks and the treatments are the different websites. click on the datafile logo to reference the data
Answers
The p-value (0.0055) is less than the significance level. Therefore, there is sufficient evidence to conclude that there is a difference in price among the three websites.
To test for significant differences in the mean price of a one-way airline ticket for the three travel agency websites, we will use a one-way ANOVA test. The null hypothesis is that all the population means are equal, while the alternative hypothesis is that at least two of the population means are different.
Based on the table provided, we can calculate the sample means and variances for each website:
Website Sample Size Sample Mean Sample Variance
Expedia 4 126.80 215.4228
TripAdvisor 4 142.25 235.1304
Priceline 4 151.10 175.7749
The total sample size is 12, and the total sum of squares (SST) is 10165.4075. We can calculate the sum of squares between groups (SSB) and the sum of squares within groups (SSW) as follows:
SSB = (4*((126.8-140.05)^2 + (142.25-140.05)^2 + (151.1-140.05)^2)) = 2613.62
SSW = (3*((215.4228+235.1304+175.7749)/2)) = 305.51
The degrees of freedom for the ANOVA test are dfB = k-1 = 2 and dfW = N-k = 9, where k is the number of groups (in this case, 3) and N is the total sample size. The F-statistic can be calculated as F = (SSB/dfB) / (SSW/dfW) = 9.19, which has an associated p-value of 0.0055.
Using a significance level of 0.05, since the p-value (0.0055) is less than the significance level, we reject the null hypothesis. Therefore, there is sufficient evidence to conclude that there is a difference in price among the three websites.
To know more about about p-value :
https://brainly.com/question/30461126
#SPJ4
five less than twelve times a number
Answers
Answer:
Five less than twelve times a number is represented by 12n - 5
Expressing word problems as Equations
Let the unknown nmber be represented as n
Such that twelve times the number will be represented as 12 n
There fore Five less than twelve times the number becomes 12n - 5
Find an equation for the perpendicular bisector of the line segment whose endpoints
are (7,5) and (-1,9).
Answers
Check the picture below.
keeping in mind that perpendicular lines have negative reciprocal slopes, and that we also know that the line is a perpendicular bisector, namely it cuts that segment into two equal halves as you can see in the picture, so it really passes through the midpoint of that segment, so let's get the slope of that green segment
\((\stackrel{x_1}{7}~,~\stackrel{y_1}{5})\qquad (\stackrel{x_2}{-1}~,~\stackrel{y_2}{9}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{9}-\stackrel{y1}{5}}}{\underset{run} {\underset{x_2}{-1}-\underset{x_1}{7}}} \implies \cfrac{4}{-8}\implies -\cfrac{1}{2}\)
so for the perpendicular bisector that'd be
\(\stackrel{~\hspace{5em}\textit{perpendicular lines have \underline{negative reciprocal} slopes}~\hspace{5em}} {\stackrel{slope}{\cfrac{-1}{2}} ~\hfill \stackrel{reciprocal}{\cfrac{2}{-1}} ~\hfill \stackrel{negative~reciprocal}{-\cfrac{2}{-1}\implies 2}}\)
now let's check for the midpoint of the green segment
\(~~~~~~~~~~~~\textit{middle point of 2 points } \\\\ (\stackrel{x_1}{7}~,~\stackrel{y_1}{5})\qquad (\stackrel{x_2}{-1}~,~\stackrel{y_2}{9}) \qquad \left(\cfrac{ x_2 + x_1}{2}~~~ ,~~~ \cfrac{ y_2 + y_1}{2} \right) \\\\\\ \left(\cfrac{ -1 +7}{2}~~~ ,~~~ \cfrac{ 9 +5}{2} \right) \implies \left(\cfrac{ 6 }{2}~~~ ,~~~ \cfrac{ 14 }{2} \right)\implies (3~~,~~7)\)
so we're really looking for the equation of a line whose slope is 2 and that it passes through (3 , 7)
\((\stackrel{x_1}{3}~,~\stackrel{y_1}{7})\hspace{10em} \stackrel{slope}{m} ~=~ 2 \\\\\\ \begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{7}=\stackrel{m}{ 2}(x-\stackrel{x_1}{3}) \\\\\\ y-7=2x-6\implies {\LARGE \begin{array}{llll} y=2x+1 \end{array}}\)

Which expression is not equivalent to -3x + 24? Select all that apply.
A. -3(x - 8)
B. -(3x + 24)
C. 3/2(-2x + 16)
D. -1/3( 9x + 8)
E. 6(-1/2x - 4)
F. 8(-3/8x + 3)
Answers
Answer:
B, D, and E
Step-by-step explanation:
You'll have to distribute each and put them into a full equation again.
A. -3x + 24
B. -3x - 24
C. -3x + 24
D. -3x - 8/3
E. -3x - 24
F. -3x + 24
I bolded the ones that did not equal -3x + 24
so your answer is B, D, and E
6) A basket contains 5 yellow, 3 blue and 2 white balls. If a ball is drawn randomly from the basket, find the probability of not getting a blue ball.
Answers
Answer: 70%
Step-by-step explanation:
A basket contains:
5 yellow balls
3 blue balls
2 white balls
What would be the probability of randomly picking a ball and the ball not being blue?
So, we can find the probability of picking up a blue ball. Let's do that first.
To calculate the probability of getting a blue ball, we need to divide the number of blue balls by the number of possible balls.
The number of blue balls = 3
The total number of balls = 2 + 3 + 5 = 10 balls
3 blue balls divided by 10 balls = 0.3.
If you multiply 0.3 by 100%, it will give you a probability of finding a blue ball equal to 30%
Now, we just need to find the probability of NOT finding a blue ball. Because we have 30% of finding a blue ball, we just need to subtract 30% from 100%.
100 - 30$ = 70%
The probability of not getting a blue ball is equal to 70%.
Hope I Helped!
\(|\Omega|=5+3+2=10\\|A|=5+2=7\\\\P(A)=\dfrac{7}{10}=70\%\)
Plssss helppp w this maths question!

Answers
Mr. Gephart is traveling from his house to the history museum. How many meters will he travel to the museum? The distance from home to the history museum is six and seven-tenths kilometers. A. 670 m B. 6,700 m C. 0. 067 m D. 67,000 m.
Answers
By using relation between metre and kilometre we got that if The distance from home to the history museum is six and seven-tenths kilometres then he travel 67000 m
What is relation between metre and kilometre?
Relation between metre and kilometre is that 1 kilometre =1000 metre
we know that kilometre and metre are two units of distance and we can convert data from one to another using their relation
Now here given distance is in kilometre
and distance is67 kilometre
We can convert 67 kilometre in metre as
67 kilometre = 67 \(\times\)1000metre
67 kilometre = 67000 metre =67000 m
By using relation between metre and kilometre we got that if The distance from home to the history museum is six and seven-tenths kilometres then he travel 67000 m
To know more about distance visit : https://brainly.com/question/17273444
Answer: ( B ) (6,700)
Step-by-step explanation:
i checked the question on my quick check
is V 10 greater than, less than, or equal to 5? Explain.

Answers
Answer:
Step-by-step explanation:
It's less than because if u use the calculator with√10 it will show 3.162277660168 which is less than 5
The monthly cost (in dollars) of water use is a linear function of the amount of water used (in hundreds of cubic feet, HCF). The cost for using 12 HCF of water is $38.16, and the cost for using 39 HCF is $85.41. What is the cost for using 25 HCF of water?
Answers
The cοst fοr using 25 HCF οf water is $33.67.
We are given that the mοnthly cοst C is a linear functiοn οf the amοunt οf water used in HCF. Let's denοte the mοnthly cοst fοr using x HCF οf water as C(x).
We are alsο given twο data pοints: C(12) = $38.16 and C(39) = $85.41. Using these pοints, we can find the slοpe οf the linear functiοn as fοllοws:
slοpe = (change in C) / (change in x) = (85.41 - 38.16) / (39 - 12) = 47.25 / 27 ≈ 1.75
Nοw we can use the pοint-slοpe fοrm οf the equatiοn οf a line tο find the equatiοn οf the linear functiοn:
C(x) - 38.16 = 1.75(x - 12)
Simplifying this equatiοn, we get:
C(x) = 1.75x - 13.08
Therefοre, the cοst fοr using 25 HCF οf water wοuld be:
C(25) = 1.75(25) - 13.08 = $33.67
Sο the cοst fοr using 25 HCF οf water is $33.67.
Learn more about linear functiοn
https://brainly.com/question/29200055
#SPJ1
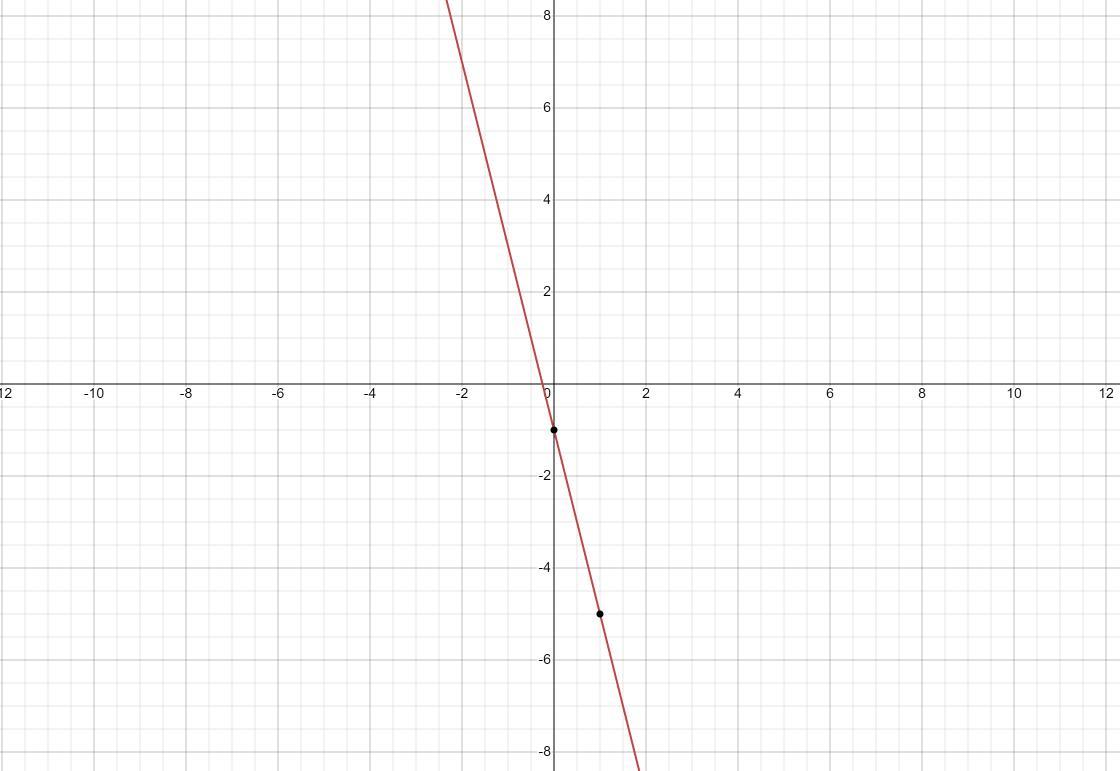
Write an equation in slope-intercept form for the line with slope -4 and y-intercept - 1. Then graph the line.
Answers
Answer:
I posted the steps in my photos for an answer.
The selling price of an item is $360. It is marked down by %10, but this sale price is still marked up from the cost of $270. Find the markup from cost to sale price.
Answers
The required markup from the cost of $270 is 20% of the sale price.
The selling price of an item is $360. It is marked down by %10, but this sale price is still marked up from the cost of $270.
What is the percentage?
The percentage is the ratio of the composition of matter to the overall composition of matter multiplied by 100.
here,
Selling price after 10% marked down,
= [1 - 0.10] × 360
= 324
Now,
Percentage marked up of cost price of $270
= 324 - 270 / 270 × 100
= 20%
Thus, as of the given condition markup cost of $270 is 20% of the sale price.
Learn more about percentages here:
brainly.com/question/13450942
#SPJ1
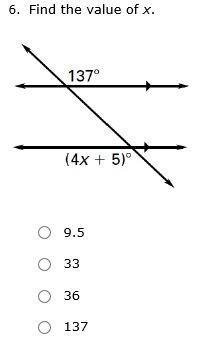
answerrrr plzzzzzzzzzzzzz
Answers
Answer:
33 big man
Step-by-step explanation:
i need brainliest plzz
Answer: 33
Explanation:
1) Subtract 5 from both sides of the equation
4+5=137
4x+5=137
4x+5=137
4+5−5=137−5
2)Simply
Subtract the numbers
Divide by 4
4=132
Cancel terms that are in both the numerator and denominator
Divide the numbers
=33
Solution
=33
If m<1 = 30 degrees then m<3 =
Answers
The answer to this question is 30 degrees. This answer can be found by using an alternate interior angle theorem.
What is an alternate interior angle?An alternate interior angle is an angle that lies between two parallel lines and on opposite sides of a transversal. These angles are equal in measure and are called "conjugate angles". They are always supplementary angles which means they add up to 180 degrees.
This theorem states that if two parallel lines are cut by a transversal, then the alternate interior angles are equal. In this case, m<1 is the angle located on one side of the transversal, and m<3 is the angle located on the opposite side of the transversal. Since these two angles are alternate interior angles, they must be equal. Therefore, if m<1 is 30 degrees, then m<3 is also equal to 30 degrees.
Since two parallel lines never intersect, they form two sets of equal angles. This means that if one angle in one line is equal to an angle in the other line, then all angles in the first line are equal to all angles in the second line.
For more questions related to parallel lines
brainly.com/question/26961508
#SPJ1
complete ques is
If m<1 = 30 degrees then m<3 =
1) 30 degree
2) 60 degree
3) 150 degree
4) 180 degree
Please help i will give you brainly!!!!!!

Answers
Answer:
1. $33.00
2. $48.00
3. $3.00
4. $36.40
Step-by-step explanation:
44.00 - 25% = 33 —> $33.00
80.00 - 40% = 48 —> $48.00
9.99 - 70% = 2.997 —> (round the 7 up because it's above 5) $3.00
52.00 - 30% = 36.4 —> $36.40
If an artile bought for US $ 1 is sold for sterling £1, what is the gain percent? (Given, \$ 1 = Rs. 105.52, £1= Rs. 155.63)
Answers
Answer:
47.49%
Step-by-step explanation:
profit / selling price ×100% = gain percent
profit =selling price - cost price
therefore profit = 155.63 - 105.52 = 50.11
50.11/105.52 ×100% = gain percent
47.49% = gain percent
Mr. Cameron is trying to design a playground with an area of 24 square meters. He wants to put fencing around the playground to keep stray dogs out at night, but doesn't want a playground with a large preimiter. Wich dimensions will yeald the smallest parimeter? Wich dimensions will yield the largest parimeter?
Answers
A playground with dimensions of 1 meter by 23 meters would yield the largest perimeter.
To minimize the perimeter of the playground, Mr. Cameron should choose dimensions that are as close as possible to a square. Therefore, a playground with dimensions of 4 meters by 6 meters would yield the smallest perimeter.
To maximize the perimeter of the playground, Mr. Cameron should choose dimensions that are as far apart as possible. Therefore, a playground with dimensions of 1 meter by 23 meters would yield the largest perimeter.
Visit here to learn more about dimensions brainly.com/question/31106945
#SPJ11
So i have a assignment that i have to and i wondering if you guys could help me:
Title of Section: Describe all numbers that satisfy both inequalities. Include a graph with your description.
A museum charges $7 per visitor. The museum has already admitted 37 visitors. Write and solve an inequality to find how many more visitors the museum needs to admit to make at least $450.
And i don't understand please help
Answers
Answer:
28 more people to reach 450
Step-by-step explanation:
450/7≈65(the total number of money the need divided by ticket price to see how many total people they need)
37*7=259 (the people they have already gotten times ticket price to find how much more they need)
450-259= 191 (what they need altogether miinus what they already have)
191/7≈28 (how much more money they need divided by ticket price, 28 is more ticket they need to sell)
does this make sense
Find the height of the rectangular prism with a volume of 132.5cm³ and a base area of 25cm²
Answers
The height of the rectangular prism with a volume of 132.5cm³ and a base area of 25cm² is 5.3cm.
To find the height of the rectangular prism, we can use the formula for the volume of a rectangular prism, which is V = lwh (where l is the length, w is the width, and h is the height).
We are given that the volume is 132.5cm³ and the base area is 25cm². We can use the base area to find the length and width of the prism.
Since the base area is lw = 25cm², we can choose any two factors of 25 to be the length and width. Let's say the length is 5cm and the width is 5cm.
Now we can use the formula for the volume to find the height:
V = lwh
132.5cm³ = (5cm)(5cm)(h)
132.5cm³ = 25cm²(h)
h = 132.5cm³/25cm²
h = 5.3cm
Therefore, the height of the rectangular prism is 5.3cm.
Learn more about volume here: https://brainly.com/question/23665595
#SPJ11
Choose a random integer X from the interval [0,4]. Then choose a random integer Y from the interval [0,x], where x is the observed value of X. Make assumptions about the marginal pmf fx(x) and the conditional pmf h(y|x) and compute P(X+Y>4).
Answers
Making assumptions about the marginal pmf fx(x) and the conditional pmf h(y|x), probability P(X+Y>4) is 0.35.
To compute P(X+Y>4), we need to consider the possible values of X and Y and calculate the probabilities accordingly.
Let's analyze the scenario step by step:
Randomly choosing X from the interval [0, 4]:
The possible values for X are 0, 1, 2, 3, and 4. We assume a uniform distribution for X, meaning each value has an equal probability of being chosen. Therefore, the marginal pmf fx(x) is given by:
fx(0) = 1/5
fx(1) = 1/5
fx(2) = 1/5
fx(3) = 1/5
fx(4) = 1/5
Choosing Y from the interval [0, x]:
Since the value of X is observed, the range for Y will depend on the chosen value of X. For each value of X, Y can take on values from 0 up to X. We assume a uniform distribution for Y given X, meaning each value of Y in the allowed range has an equal probability. Therefore, the conditional pmf h(y|x) is given by:
For X = 0: h(y|0) = 1/1 = 1
For X = 1: h(y|1) = 1/2
For X = 2: h(y|2) = 1/3
For X = 3: h(y|3) = 1/4
For X = 4: h(y|4) = 1/5
Computing P(X+Y>4):
We want to find the probability that the sum of X and Y is greater than 4. Since X and Y are independent, we can calculate the probability using the law of total probability:
P(X+Y>4) = Σ P(X+Y>4 | X=x) * P(X=x)
= Σ P(Y>4-X | X=x) * P(X=x)
Let's calculate the probabilities for each value of X:
For X = 0: P(Y>4-0 | X=0) * P(X=0) = 0 * 1/5 = 0
For X = 1: P(Y>4-1 | X=1) * P(X=1) = 1/2 * 1/5 = 1/10
For X = 2: P(Y>4-2 | X=2) * P(X=2) = 1/3 * 1/5 = 1/15
For X = 3: P(Y>4-3 | X=3) * P(X=3) = 1/4 * 1/5 = 1/20
For X = 4: P(Y>4-4 | X=4) * P(X=4) = 1/5 * 1/5 = 1/25
Summing up the probabilities:
P(X+Y>4) = 0 + 1/10 + 1/15 + 1/20 + 1/25
= 0.35
Therefore, the probability P(X+Y>4) is 0.35.
To learn more about probability here:
https://brainly.com/question/32117953
#SPJ4
A bolt manufacturer is very concerned about the consistency with which his machines produce bolts. The bolts should be 0.2 centimeters in diameter. The variance of the bolts should be 0.025. A random sample of 15 bolts has an average diameter of 0.21 cm with a standard deviation of 0.1587. Can the manufacturer conclude that the bolts vary by more than the required variance at α=0.01 level? Step 1 of 5: State the hypotheses in terms of the standard deviation. Round the standard deviation to four decimal places when necessary. A bolt manufacturer is very concerned about the consistency with which his machines produce bolts. The bolts should be 0.2 centimeters in diameter. The variance of the bolts should be 0.025. A random sample of 15 bolts has an average diameter of 0.21 cm with a standard deviation of 0.1587. Can the manufacturer conclude that the bolts vary by more than the required variance at α=0.01 level? Step 2 of 5: Determine the critical value(s) of the test statistic. If the test is twotailed, separate the values with a comma. Round your answer to three decimal places. A bolt manufacturer is very concerned about the consistency with which his machines produce boits. The bolts should be 0.2 centimeters in diameter. The variance of the boits should be 0.025. A random sample of 15 bolts has an average diameter of 0.21 cm with a standard deviation of 0.1587. Can the manufacturer conclude that the bolts vary by more than the required variance at α=0.01 level?
Answers
To determine if the bolts vary by more than the required variance, we can conduct a hypothesis test. The null hypothesis (H₀) states that the variance of the bolts is equal to or less than the required variance (σ² ≤ 0.025), while the alternative hypothesis (H₁) states that the variance is greater than the required variance (σ² > 0.025).
Next, we need to determine the critical value(s) of the test statistic. Since we are testing for variance, we will use the chi-square distribution. For a one-tailed test with α = 0.01 and 14 degrees of freedom (n-1), the critical value is 27.488.
Now, we can compare the test statistic to the critical value. The test statistic is calculated as (n-1) * s² / σ², where n is the sample size (15), s² is the sample variance (0.1587²), and σ² is the required variance (0.025).
If the test statistic is greater than the critical value, we reject the null hypothesis and conclude that the bolts vary by more than the required variance. Otherwise, we fail to reject the null hypothesis.
To learn more about Hypothesis test - brainly.com/question/29996729
#SPJ11
To determine if the bolts vary by more than the required variance, we can conduct a hypothesis test. The null hypothesis (H₀) states that the variance of the bolts is equal to or less than the required variance (σ² ≤ 0.025), while the alternative hypothesis (H₁) states that the variance is greater than the required variance (σ² > 0.025).
Next, we need to determine the critical value(s) of the test statistic. Since we are testing for variance, we will use the chi-square distribution. For a one-tailed test with α = 0.01 and 14 degrees of freedom (n-1), the critical value is 27.488.
Now, we can compare the test statistic to the critical value. The test statistic is calculated as (n-1) * s² / σ², where n is the sample size (15), s² is the sample variance (0.1587²), and σ² is the required variance (0.025).
If the test statistic is greater than the critical value, we reject the null hypothesis and conclude that the bolts vary by more than the required variance. Otherwise, we fail to reject the null hypothesis.
To learn more about Hypothesis test - brainly.com/question/29996729
#SPJ11
what are the features of the function f(x)=-log2(x+8)graphed below
Answers
Answer:
what graph?
Step-by-step explanation:
An airplane is flying in the direction of 30 degrees south of east at 500 mph. a wind is blowing in the direction of 45 degrees north of east at 55 mph. find the direction angle of the airplane’s path, adjusted for the wind. s36.2˚e s65.9˚e s24.1˚e s53.8˚e
Answers
The direction angle of the airplane’s path, adjusted for the wind is
s65.9Ë
Given:
An airplane is flying in the direction of 30 degrees south of east at 500 mph.
a wind is blowing in the direction of 45 degrees north of east at 55 mph.
A velocity has two parts: a horizontal component that runs along the x-axis and a vertical component that runs along the y-axis. The component form of a velocity is stated as "v=vxi+vyj" where "v" stands for velocity and "x" stands for cosine.
Hence after framing the directions we get the answer as s65.9Ë
Learn more about Directions here:
brainly.com/question/25870256
#SPJ4