A solution contains 0.112 M potassium nitrite and 0.347 M nitrous acid (Ka = 4.5 x 10-4) The pH of this solution is Submit Answer Retry Entire Group 1 more group attempt remaining
Answers
The pH of the solution cannot be determined solely from the given information of the concentrations of potassium nitrite and nitrous acid. Additional information, such as the volume of the solution, is required to calculate the pH accurately.
To determine the pH of the solution containing potassium nitrite and nitrous acid, we need to consider the acid-base properties of nitrous acid (HNO2) and its conjugate base nitrite ion (NO2-).
Nitrous acid (HNO2) is a weak acid that can partially dissociate in water:
HNO2 ⇌ H+ + NO2-
The equilibrium constant for this reaction is given by the acid dissociation constant (Ka), which is 4.5 x 10^(-4).
First, we need to calculate the concentration of H+ ions resulting from the dissociation of nitrous acid. Since nitrous acid and potassium nitrite are in the same solution, we can assume that the nitrous acid concentration is equal to the concentration of H+ ions.
Next, we can use the formula for the pH of a solution:
pH = -log[H+]
To calculate the pH, we need to determine the concentration of H+ ions from nitrous acid using the given concentrations of potassium nitrite and nitrous acid.
However, the concentration of H+ ions cannot be determined solely from the concentration of nitrous acid and potassium nitrite. Additional information, such as the volume of the solution, is needed to calculate the pH accurately.
Know more about pH here:
https://brainly.com/question/2288405
#SPJ11
Related Questions
Write the inverse of the function: f (x) = 2x+3
Answers
Answer:
\(y = \frac{x - 3}{2}\)
Step-by-step explanation:
To find the inverse of a function, simply 'switch' the x and y's and solve for y. \(y = 2x + 3\) becomes \(x = 2y + 3\). Now, solving for y, we get \(y = \frac{x - 3}{2}\).
hope this helped! :)
How much does a 5 gallon of water weigh?
Answers
A 5-gallon container of water weighs approximately 41.7 pounds (18.9 kilograms). This is because water has a density of 1 kilogram per liter or 8.34 pounds per gallon. Therefore, a 5-gallon container holds 18.9 liters of water, which weighs 18.9 kilograms or 41.7 pounds.
A gallon of water is equivalent to 8.34 pounds of water. So 5-gallon of water is equivalent to
= 5 * 8.34
= 41.70
A gallon of water is equivalent to 3.78 litres of water. So 5-gallon of water is equivalent to
= 5 * 3.78
= 18.90
A litre of water is equivalent to 1 kilogram of water. So 18.90 litres of water is equivalent to
= 18.90 * 1
= 18.90
To know more on gallon
https://brainly.com/question/1462470
#SPJ4
(b) Given the matrix D = k 0 0 3 k² k³ 0 kª k³ kº k k k 0 0 0 k¹⁰ Find all possible value(s) of k if det(D) = 1024."
Answers
To find the possible values of k, we need to calculate the determinant of matrix D and set it equal to 1024.
Given matrix D:
D = | k 0 0 |
| 3 k² k³ |
| 0 kª k³ kº |
| k k k |
| 0 0 0 |
| k¹⁰ |
The determinant of D can be calculated by expanding along the first row or the first column. Let's expand along the first row:
det(D) = k(det | k³ k k |
| 0 k³ kº |
| 0 0 k¹⁰ |)
- 0(det | 3 k² k³ |
| 0 kª k³ |
| k k k |)
+ 0(det | 3 k² k³ |
| k k k |
| k k k |)
Simplifying further, we have:
det(D) = k(det | k³ k k |
| 0 k³ kº |
| 0 0 k¹⁰ |)
Now, we can calculate the determinant of the 3x3 submatrix:
det | k³ k k |
| 0 k³ kº |
| 0 0 k¹⁰ |
This determinant can be found by expanding along the first row or the first column. Expanding along the first row gives us:
det = k(k³(kº) - 0(k)) - 0(0(k¹⁰)) = k⁴kº = k⁴+kº
Now, we can set det(D) equal to 1024 and solve for k:
k⁴+kº = 1024
Since we are looking for all possible values of k, we need to solve this equation for k. However, solving this equation may require numerical methods or approximations, as it is a quartic equation.
Learn more about matrix here
https://brainly.com/question/2456804
#SPJ11
Pls Help I hate math

Answers
Answer:
b
Step-by-step explanation:
to find the volume of the figure you have to multiply the with times the length times the height
2x12x9=216
In a pack of candies, Marla found that for every 3 blue candies, there were 5 red ones. Identify the correct list of ratios that compares the red candies to the blue ones.
3
5
; 5 to 3; 5:3
5
3
; 5 to 3; 5:3
3
5
; 3 to 5; 3:5
5
3
; 3 to 5; 3:5
Answers
Answer:
B
Step-by-step explanation:
Red goes first then blue
5:3
Answer:
5
3
; 5 to 3; 5:3
Step-by-step explanation:

Consider the density curve plotted below:1920212223240.0250.050.0750.10.1250.150.1750.20.2250.250.275XPDF(X)Density CurveFind P(X≤22) : 0.1Find P(X>21) : Calculate the following. Q1: median: Q3: IQR:

Answers
In this problem, we have a graph of the PDF (Probability Density Function). To compute probabilities in a certain interval (a, b), we must integrate this function from x = a to x = b.
(1) P(X ≤ 22)
We integrate the function from x = -∞ to x = 22, we get:
\(\begin{gathered} P(X\text{ }≤\text{ }22)=\int_{-\infty}^{22}dx\cdot PDF(x) \\ =\int_{-\infty}^{20}dx\cdot PDF(x)+\int_{20}^{22}dx\cdot PDF(x) \\ =\int_{-\infty}^{20}dx\cdot0+\int_{20}^{22}dx\cdot0.25 \\ =0+0.25\cdot(22-20) \\ =0.25\cdot2 \\ =0.5. \end{gathered}\)We separated the integral to use the data from the graph.
(2) P(X > 21)
We integrate the function from x = 21 to x = ∞, we get:
\(\begin{gathered} P(X>21)=\int_{21}^{\infty}dx\cdot PDF(x) \\ =\int_{21}^{24}dx\cdot PDF(x)+\int_{24}^{\infty}dx\cdot PDF(x) \\ =\int_{21}^{24}dx\cdot0.25+\int_{24}^{\infty}dx\cdot0 \\ =0.25\cdot(24-21)+0 \\ =0.25\cdot3 \\ =0.75. \end{gathered}\)(3) The Q1 is the value x = a of the interval (-∞, a) that gives a probability equal to 0.25. So we must find x such that:
\(P(XUsing the data of the graph, we have:\(\begin{gathered} \int_{-\infty}^adx\cdot PDF(x)+\int_{20}^adx\cdot PDF(x)=0.25, \\ \int_{-\infty}^{20}dx\cdot0+\int_{20}^adx\cdot0.25=0.25, \\ 0.25\cdot(a-20)=0.25, \\ a-20=\frac{0.25}{0.25}, \\ a-20=1, \\ a=21. \end{gathered}\)(4) The median is the value x = a of the interval (-∞, a) that gives a probability equal to 0.5. Proceeding as before, we have:
\(\begin{gathered} \int_{-\infty}^adx\cdot PDF(x)+\int_{20}^adx\cdot PDF(x)=0.5, \\ \int_{-\infty}^{20}dx\cdot0+\int_{20}^adx\cdot0.25=0.5, \\ 0.25\cdot(a-20)=0.5, \\ a-20=\frac{0.5}{0.25}, \\ a-20=2, \\ a=22. \end{gathered}\)(5) The Q3 is the value x = a of the interval (-∞, a) that gives a probability equal to 0.75. Proceeding as before, we have:
\(\begin{gathered} \int_{-\infty}^adx\cdot PDF(x)+\int_{20}^adx\cdot PDF(x)=0.75, \\ \int_{-\infty}^{20}dx\cdot0+\int_{20}^adx\cdot0.25=0.75, \\ 0.25\cdot(a-20)=0.75, \\ a-20=\frac{0.75}{0.25}, \\ a-20=3, \\ a=23. \end{gathered}\)(6) The IQR is given by the difference between Q3 and Q1. Using the results from above, we get:
\(IQR=Q3-Q1=23-21=2.\)Answer• P(X ≤ 22) = 0.5
,• P(X > 21) = 0.75
,• Q1 = 21
,• median = 22
,• Q3 = 23
,• IQR = 2
which function is the inverse of fx -5x-4
I don’t know which one it is

Answers
Answer:
A) \(f^{-1}(x)=-\frac{1}{5}x-\frac{4}{5}\)
Step-by-step explanation:
\(f(x)=-5x-4\\y=-5x-4\\x=-5y-4\\x+4=-5y\\-\frac{1}{5}x-\frac{4}{5}=y\\\\f^{-1}(x)=-\frac{1}{5}x-\frac{4}{5}\)
When finding the inverse of a function, we switch the values of x and y, and then solve for y, like in the 3rd-6th steps.
I don’t understand
My teacher never showed us how to workout these problems so can y’all please SHOW WORK so I can do on the following questions coming up ty <3 (algebra 1)

Answers
Answer:
Step-by-step explanation:
The area of a parallelogram is base times height.
In this case it would be:
(3x +1) (5x-4)
Then multiply to simplify.
Use FOIL
15x² - 12x + 5x - 4
Simplify again
15x² - 7x - 4
What’s the measurement of
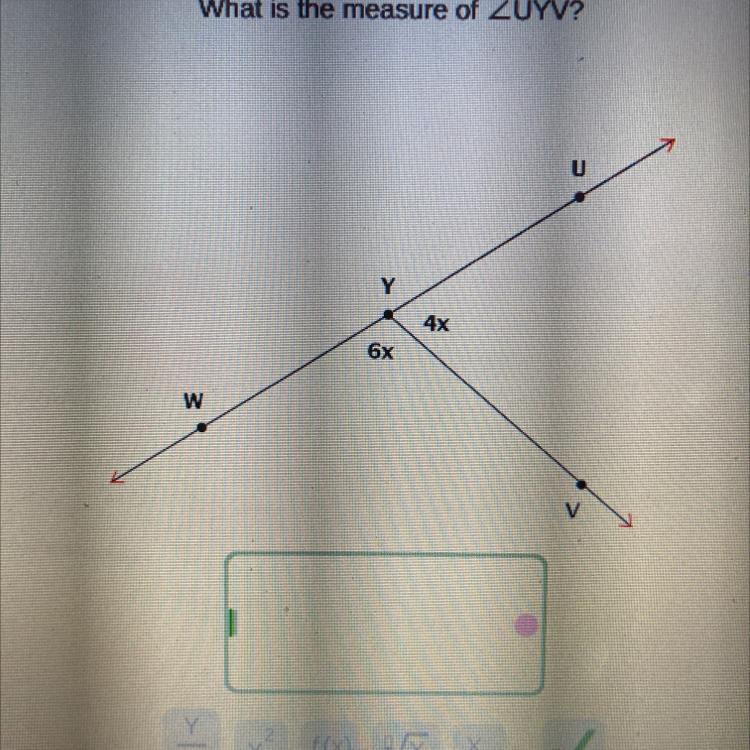
Answers
Step-by-step explanation:
4x and 6x sit on a straight line therefore must equal to 180°
4x+6x = 180° (∠'s on str. line)
10x = 180
x= 180/10
x= 18
Then we need to find ∠UYV
∠UYV = 4x
=4(18)
=72°
So ∠UYV = 72°
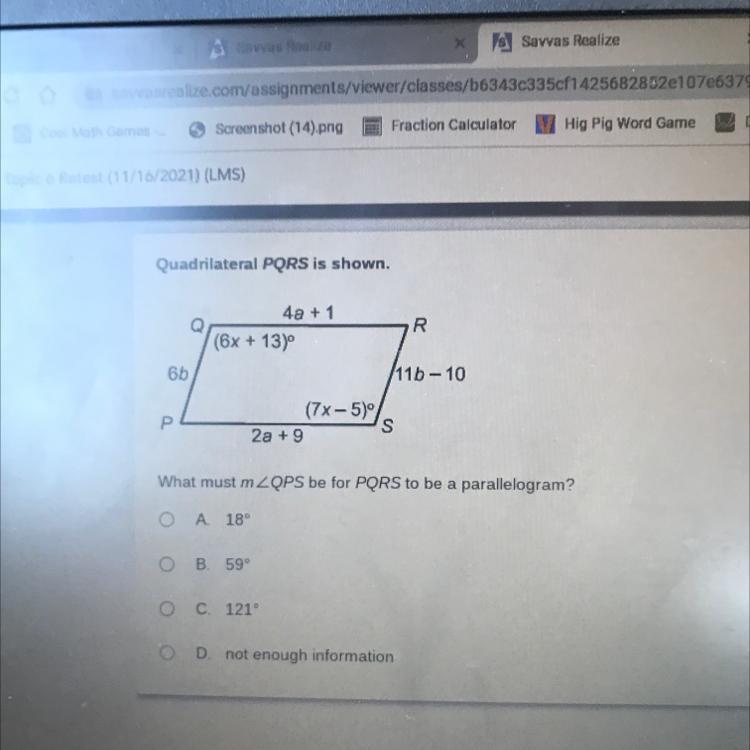
Quadrilateral PQRS is shown
40+1
Q
R
(6x + 13)
6b
/11b-10
(7x- 500
P
s
2a +9
What must mZQPS be for PORS to be a parallelogram?
A 18
B 59
C 121
OD not enough information
Answers
Answer:
m∠QPS = 59
Step-by-step explanation:
59 + (7x-5) = 180
x = 18
If you substitute 59 with the other answer options you will get a decimal.
I hope that this could help!!!!
Write the equation that describes the simple harmonic motion of a particle moving uniformly around a circle of radius 7 units, with angular speed 2 radians per second.
Answers
The phase angle (φ) represents the Initial position of the particle at time t = 0. Depending on the specific starting position.
The equation that describes the simple harmonic motion of a particle moving uniformly around a circle can be given by:
x(t) = A * cos(ωt + φ)
In this equation, x(t) represents the displacement of the particle from the center of the circle at time t. A represents the amplitude of the motion, which is the maximum displacement from the center. ω represents the angular frequency or angular speed of the motion, given in radians per unit of time. φ represents the phase angle or initial phase of the motion.
In the given scenario, the particle is moving uniformly around a circle of radius 7 units. The angular speed is 2 radians per second. Since the particle is moving uniformly, the angular frequency (ω) is equal to the angular speed (2 radians per second). The radius of the circle is 7 units, which represents the amplitude (A) of the motion.
Substituting the values into the equation, we get:
x(t) = 7 * cos(2t + φ)
The phase angle (φ) represents the initial position of the particle at time t = 0. Depending on the specific starting position, the value of φ may vary.
the simple harmonic motion of the particle moving around the circle. The cosine function represents the periodic nature of the motion, with the particle oscillating back and forth along the circumference of the circle with the given amplitude and angular frequency.
To know more about Initial position.
https://brainly.com/question/30327255
#SPJ11
Measure the lengths of the following segments in BOTH centimeters and millimeters

Answers
\(1 cm = 100 mm\)Answer:
A) 4.3 cm
0.043 mm
B)7.2 cm
0.072 mm
An item costs $430 before tax, and the sales tax is $12.90. Find the sales tax rate. Write your answer a a percentage
Answers
Answer: The sales tax rate is 3%.
Step-by-step explanation: $12.90 is 3% of $430.
The sales tax rate is approximately 3%.
To find the sales tax rate, we can divide the amount of sales tax by the cost of the item before tax, and then multiply by 100 to express it as a percentage.
Given that the item costs $430 before tax and the sales tax is $12.90, we can calculate the sales tax rate as follows:
Sales tax rate = (Sales tax / Cost before tax) * 100
Sales tax rate = ($12.90 / $430) * 100
Sales tax rate ≈ 0.03 * 100
Sales tax rate ≈ 3%
Therefore, the sales tax rate is approximately 3%.
To know more about sales tax rate click here :
https://brainly.com/question/29751934
#SPJ2
a normal distribution has a mean of 61 and a standard deviation of 14. what is the median? (enter an exact number as an integer, fraction, or decimal.)
Answers
The median of a normal distribution with a mean of $\mu$ and standard deviation of $\sigma$ is simply equal to the mean $\mu$. Therefore, for a normal distribution with a mean of 61 and a standard deviation of 14, the median is also 61.
This is because the normal distribution is a symmetric distribution, with the mean, median, and mode all located at the same point on the horizontal axis. The mean represents the center of the distribution and is also the balance point for the distribution, so half of the observations will be less than the mean and half will be greater than the mean.
Therefore, for a normal distribution with a given mean and standard deviation, we can use the mean as an estimate of the median. In this case, the mean is exactly equal to the median, so the median is 61.
It is worth noting that this property of normal distributions only holds for normal distributions, and not necessarily for other types of distributions. For example, in a skewed distribution, the mean and median may be quite different from each other.
For more details about median click here:
https://brainly.com/question/28060453#
#SPJ11
A rectangular box is 11in and wide 11 in tall and 7 in long what is the diameter of the smallest circular opening through which box will fit
Answers
Answer:
= 1424.775 in ^3
Step-by-step explanation:
Find the slope of the line passing through the points (-5,3) and (7,9)
Answers
determine which point from the specified set satisfies the system of equations. y=3x−3 and y=−x 2
Answers
There are two points that satisfy the system of equations:
(0.79, 0.37)
(-3.79, -12.37)
The system of equations is:
y = 3x - 3
y = -x^2
To determine which point from a specified set satisfies the system of equations, we need to find the values of x and y that satisfy both equations simultaneously.
Substituting y = 3x - 3 into the second equation, we get:
3x - 3 = -x^2
Rearranging this equation, we get:
x^2 + 3x - 3 = 0
Using the quadratic formula, we can solve for x:
x = (-3 ± sqrt(3^2 - 41(-3))) / (2*1) = (-3 ± sqrt(21)) / 2
Therefore, there are two possible values of x that satisfy the system of equations:
x = (-3 + sqrt(21)) / 2 ≈ 0.79
x = (-3 - sqrt(21)) / 2 ≈ -3.79
To find the corresponding values of y, we can substitute these values of x into either equation. For example, if we use y = 3x - 3, we get:
y ≈ 0.37 (when x ≈ 0.79)
y ≈ -12.37 (when x ≈ -3.79)
Therefore, there are two points that satisfy the system of equations:
(0.79, 0.37)
(-3.79, -12.37)
To know more about Equations :
https://brainly.com/question/13865224
#SPJ11
Ascume Inat the number of now vivitors to a website in onve hour is distitudted as a Posson random vaiatila. The ineain number of new visitore to the wobsitn is 2.3 por hour. Complete parts (a) through (d) bolow a. What is the probability that in any given hour zero new visitors will arrive at the website? The probability that zero new visitors will arrive is (Round to four decimal places as needed.) b. What is the probability that in any given hour exactly one new visitor will arrive at the website? The probability that exactly ohe new visitor will arrive is (Round to four decimal places as needed.) c. What is the probability that in any given hour two or more new visitors will arrive at the website? The probability that two or more new visitors will arrive is (Round to four decimal places as needed.) d. What is the probability that in any given hour fewer than three new visitors will arrive at the website?
Answers
The probability that in any given hour fewer than three new visitors will arrive at the website is 0.5948.
a) The probability that in any given hour zero new visitors will arrive at the website is given by;P(X = 0) = (e^-λ λ^0)/0!Where λ = 2.3Thus;P(X = 0) = (e^-2.3 2.3^0)/0!P(X = 0) = (0.1003)/1P(X = 0) = 0.1003b) The probability that in any given hour exactly one new visitor will arrive at the website is given by;P(X = 1) = (e^-λ λ^1)/1!Where λ = 2.3Thus;P(X = 1) = (e^-2.3 2.3^1)/1!P(X = 1) = (0.2303)/1P(X = 1) = 0.2303c) The probability that in any given hour two or more new visitors will arrive at the website is given by;P(X ≥ 2) = 1 - P(X = 0) - P(X = 1)Thus;P(X ≥ 2) = 1 - 0.1003 - 0.2303P(X ≥ 2) = 0.6694d) The probability that in any given hour fewer than three new visitors will arrive at the website is given by;P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2)Thus;P(X < 3) = 0.1003 + 0.2303 + 0.2642P(X < 3) = 0.5948Therefore,The probability that in any given hour zero new visitors will arrive at the website is 0.1003.The probability that in any given hour exactly one new visitor will arrive at the website is 0.2303.The probability that in any given hour two or more new visitors will arrive at the website is 0.6694.The probability that in any given hour fewer than three new visitors will arrive at the website is 0.5948.
Learn more about Probability
brainly.com/question/30034780
#SPJ4
Sissy wants to enlarge a picture of a constellation so that she can put it on the wall in her daughter’s room. What will be the area of the enlarged picture on the wall?
24 in.2
108 in.2
224 in.2
486 in.2
Answers
Answer: 486 in
Just did this on edge
The enlargement transformation applied to the rectangular figure gives
a rectangle that is enlarged and similar to the figure.
Correct response:
The area of the enlarged picture is 486 in.²The given dimensions of the picture are;
Height, \(\overline{MN}\) = 6 in.
Width, \(\overline{LP}\) = 4 in.
The length of QL' = 12 + 42 = 54
By similar triangles, we have;
\(\dfrac{\overline{L'P'}}{\overline{LP}} = \mathbf{ \dfrac{\overline{QL'}}{\overline{QL}}}\)
Which gives;
\(\dfrac{\overline{L'P'}}{6} = \mathbf{ \dfrac{54}{12}}\)
\(\overline{L'P'} = \dfrac{54 }{12} \times 6 = \mathbf{27}\)
Given that an enlargement gives similar figures, we have;
\(\dfrac{\overline{L'P'}}{\overline{LP}} = \mathbf{\dfrac{\overline{L'M'}}{\overline{LM}}} = Scale \, factor \ of \ the \ enlargement\)
Therefore;
\(\dfrac{27}{6} = \dfrac{\overline{L'M'}}{4}\)
Which gives;
\(\overline{L'M'} = \dfrac{27}{6} \times 4 = \mathbf{ 18}\)
The area of the enlarged picture is, A = \(\overline{L'M'}\) × \(\overline{L'P'}\)
Which gives;
A = 27 × 18 = 486
The area of the enlarged picture on the wall is A = 486 in.²
Learn more about scale factors and enlargement transformation here:
https://brainly.com/question/14215765
https://brainly.com/question/2839518

2. (25 points) Solve (3x² + y)dx + (x²y-x) dy = 0. Do not put an absolute value in your integrating factor. (Hint: This equation is not exact)
Answers
An equation in mathematics known as a differential equation connects a function to its derivatives. It involves the derivatives of one or more unknown functions with regard to one or more independent variables.
We can use the method of precise equations to resolve the differential equation (3x2 + y)dx + (x2y - x)dy = 0 that is presented.
In order to determine whether the equation is precise, we must first determine whether (M)/(y) = (N)/(x), where M = 3x2 + y and N = x2y - x.
We have the following partial derivatives:
(M)/(y) = 1 and
(N)/(x) = 2xy - 1
The equation is not accurate because (M)/(y) does not equal (N)/(x).
We must identify an integrating factor in order to make the equation exact. We can calculate it by multiplying
(M)/(y) by (N)-(N)/(x).
Integrating factor is equal to [(M/y)]. N-(N)/(x)
= 1 / (2xy - 2xy + 1).
=1
Multiplying the entire equation by the integrating factor, we get:
(3x² + y)dx + (x²y - x)dy = 0
Since the integrating factor is 1, the equation remains unchanged.
Next, we integrate both sides of the equation with respect to x and y, treating the other variable as a constant.
Integrating the first term with respect to x, we get:
∫(3x² + y)dx = x³ + xy + C1(y)
Integrating the second term with respect to y, we get:
∫(x²y - x)dy = x²y²/2 - xy + C2(x)
Combining the two integrated terms, we have:
x³ + xy + C1(y) + x²y²/2 - xy + C2(x) = C
Simplifying, we can write the solution as:
x³ + x²y²/2 + C1(y) + C2(x) = C
To know more about Differential Equation visit:
https://brainly.com/question/25731911
#SPJ11
Help me I need help!

Answers
Answer:
56°÷
Step-by-step explanation:
The sum of the central angles in a circle is 360°. That means unmarked angle RUS is ...
360° -111° -137° = 112°
Inscribed angle RTS is half the measure of central angle RUS, so ...
∠RTS = 112°/2 = 56°
MULTIPLE CHOICE QUESTION
Is this my final answer?
No, we need to subtract that from the total
No, we need to add that to the total
Yes, the question was asking how much sales tax
we paid
Rewatch
Submit
Answers
Answer:
i don't understand the question sorry
in the expression 2^4, 4 is called the
Answers
Answer:
4 is the exponent.
Step-by-step explanation:

In the expression, 2⁴. 4 is called the exponents.
What is an exponential function?Mathematical functions with exponents include exponential functions. f(x) = bˣ, where b > 0, is a fundamental exponential function.
Given:
An expression, 2⁴.
In the expression,
4 is the exponents.
Therefore, 4 is called the exponents.
To learn more about the exponential;
https://brainly.com/question/14344314
#SPJ2
A rectangle that is 4 inches by 3 inches has been scaled by a factor of 6.
1. What are the side lengths of the scaled copy?
2. Suppose you want to scale the copy back to its original size. What scale
factor should you use?

Answers
Answer:
bq
Step-by-step explanation:
(7x² + 3x + 5) + (4x²-3)
Answers
Simplify:
\((7x^2+3x+5)+(4x^2-3)\)Explanation:
\(\begin{gathered} (7x^2+3x+5)+(4x^2-3) \\ =11x^2+3x+2 \\ \end{gathered}\)\(\)A triangle has vertices at (1,3),(2,-3), and (-1,-1). What is the approximate perimeter of the triangle? A. 16 B: 14 C: 15 D: 10
Answers
Answer:
B 14
explanation:
i did the math
The perimeter of the given triangle is 14 units, so the correct option is B.
How to get the perimeter of the triangle?
The perimeter of the triangle will be equal to the sum between the distances between the given points.
Remember that the distance between two points is (x₁, y₁) and (x₂, y₂) is:
\(d = \sqrt{(y_2 - y_1)^2 + (x_2 - x_1)^2}\)
For the pair of (1,3), (2,-3): the distance is:
\(d = \sqrt{(2 - 1)^2 + (-3 - 3)^2} = 6.08\)
For the pair (1, 3) , (-1, -1) the distance is:
\(d = \sqrt{(-1 - 1)^2 + (-1 - 3)^2} = 4.5\)
For the pair (2, -3) and (-1, -1) the distance is:
\(d = \sqrt{(2 - (-1))^2 + (-3 - (-1))^2} = 3.6\)
Then the total perimeter, rounded to the next whole number is:
6.08 + 4.5 + 3.6 = 14
So the correct option is B.
If you want to learn more about triangles, you can read:
https://brainly.com/question/4289712
The total cost to fix your bike is $45. The parts cost
$10, and
the labor cost is $7 per hour. How many hours did it
take?
Answers
Answer:
It took 5 hours
Step-by-step explanation:
45 = 10 + 7x
35 = 7x
5 = x
Steve washed 15 cars in 3 hours. How many cars can he wash in 7 hours?
Answers
Answer:35 cars in 7 hours.
Step-by-step explanation:15/3=5 per hour. 5x7=35.
Answer:
35 cars in 7 hrs
Step-by-step explanation:
Steve's rate of work is (15 cars) / (3 hrs), or 5 cars/hr.
In 7 hrs he can wash
5 cars
---------- * 7 hrs = 35 cars in 7 hrs
hr
Identify the null and alternative hypotheses in the following scenario. To determine if high-school students sleep less than middle-school students, the mean sleep times of the two groups are compared. Forty students of each level are randomly sampled and tested. Both populations have normal distributions with unknown standard deviations. a. H0 :μ1 =−μ2 ;Ha :μ1 <−μ2
b. H0 :μ1 =μ2 ;Ha :μ1 >−μ2
c. H0 :μ1 =μ2 ;Ha :μ1 −μ2
d. H0 :μ1 =−μ2 ;Ha :μ1 >−μ2
e. H0 :μ1 =−μ2 ;Ha :μ1 <μ2
Answers
The correct option is a. H0 :μ1 =−μ2 ;Ha :μ1 <−μ2. Here, the null hypothesis (H0) is the statement being tested, which states that there is no significant difference between the means of two populations, i.e., the mean sleep times of high-school students and middle-school students are equal.
Thus, the null hypothesis is given by:H0: μ1 = μ2where μ1 is the population mean of high-school students, and μ2 is the population mean of middle-school students.The alternative hypothesis (Ha) is the statement that is true if the null hypothesis is rejected.
It is the opposite of the null hypothesis, i.e., there is a significant difference between the means of two populations, i.e., the mean sleep times of high-school students and middle-school students are not equal. Thus, the alternative hypothesis is given by:Ha: μ1 < μ2The option that represents these hypotheses is a. H0 :μ1 =−μ2 ;Ha :μ1 <−μ2.
To know more about populations visit:
https://brainly.com/question/30935898
#SPJ11
If m∠3 = 78°, what is m∠4?
Answers
90, They are measuring the same, therefore m4 = 90. Four right angles are produced when two lines overlap to form single right position.
Angle, what is it?Two full lines or rays intersect at a same terminus to make an angle. The centroid of an angle is the point at which all points meet. Angle is derived from the Latin word angulus, which means "corner."
How do you recognize a correct angle?Right angles are created when two straight lines cross at a 90° angle or are identical to one another at the intersection. The sign stands for a right angle.
To know more about intersection visits:
https://brainly.com/question/14217061
#SPJ1