A shop sells three brands of light bulb. Brand A bulbs last for 560 days each. Brand B bulbs last for 600 days each. Brand C bulbs last for 580 days each. Calculate the cost of 1 day's use for 1 bulb in each brand. Give your answers in pence to 3 dp. Write the brand that is best value in the comment box
Answers
The cost per day for each brand are: Brand A: $0.01161, Brand B: $0.01300, Brand C: $0.00931. The best value brand is Brand C.
To calculate the cost per day for each brand, we divide the cost by the number of days:
Cost per day for Brand A = Cost of Brand A bulb / Number of days for Brand A
Cost per day for Brand B = Cost of Brand B bulb / Number of days for Brand B
Cost per day for Brand C = Cost of Brand C bulb / Number of days for Brand C
To determine the best value brand, we compare the cost per day for each brand and select the brand with the lowest cost.
Let's assume the costs of the bulbs are as follows:
Cost of Brand A bulb = $6.50
Cost of Brand B bulb = $7.80
Cost of Brand C bulb = $5.40
Calculating the cost per day for each brand:
Cost per day for Brand A = $6.50 / 560
≈ $0.01161
Cost per day for Brand B = $7.80 / 600
≈ $0.01300
Cost per day for Brand C = $5.40 / 580
≈ $0.00931
Comparing the costs, we see that Brand C has the lowest cost per day. Therefore, Brand C provides the best value among the three brands.
Learn more about cost here:
https://brainly.com/question/29176074
#SPJ11
Related Questions
If both p and 2p+1 are prime, then 2p+1 is a safe prime and p is what other kind of prime, whose namesake—the first woman to win a prize from the Paris Academy of Sciences, for work on elasticity—used them to investigate Fermat's Last Theorem?
Answers
If both p and 2p+1 are prime, then 2p+1 is a safe prime and p is a Sophie Germain prime.
Sophie Germain was a French mathematician who used these primes to investigate Fermat's Last Theorem, a famous mathematical conjecture that was finally proved in 1994 by Andrew Wiles. A safe prime is a prime number of the form 2p+1, where p is also a prime number, and it is called "safe" because it has some cryptographic properties that make it useful in certain encryption schemes. In number theory, Fermat's Last Theorem (sometimes called Fermat's conjecture, especially in older texts) states that no three positive integers a, b, and c satisfy the equation an + bn = cn for any integer value of n greater than 2. The cases n = 1 and n = 2 have been known since antiquity to have infinitely many solutions.
Learn more about safe prime here, https://brainly.com/question/145452
#SPJ11
A scale model of a house uses a scale 1/4 (faction)
inch = 3 feet. If the model is 4.25
inches tall, what is the actual height of the
house?
Answers
Answer: The actual height of the house is 17 feet.
Step-by-step explanation:
The actual height of the house can be found by multiplying the model's height (4.25 inches) by the scale factor.
4.25 inches * 4 (3 feet/1/4 inch) = 17 feet.
So the actual height of the house is 17 feet.
option D: 8 square root 3 cm
pls help
thanks

Answers
Answer:
is b
Step-by-step explanation:

. suppose that urn contains 3 red balls, 5 blue balls, and 2 green balls. we draw randomly 3 balls from the urn without replacement, one-by-one. let x denote the number of red balls chosen, and let y denote the number of blue balls chosen. find corr(x, y ).
Answers
By using the concept of probability, it can be calculated that
Corr(X, Y) = 0.5705
What is probability?
Probability gives us the information about how likely an event is going to occur
Probability is calculated by Number of favourable outcomes divided by the total number of outcomes.
Probability of any event is greater than or equal to zero and less than or equal to 1.
Probability of sure event is 1 and probability of unsure event is 0.
Here, concept of probability will be used
An urn contains 3 red balls, 5 blue balls, and 2 green balls.
Let X denote the number of red balls chosen and let Y denote the number of blue balls chosen.
P(X = 0) = \(\frac{{3 \choose 0}{ 5 \choose 1 }{ 2 \choose 2}}{{10 \choose 3}}}+ \frac{{3 \choose 0}{ 5 \choose 2 }{ 2 \choose 1}}{{10 \choose 3}}} = \frac{25}{120}\)
P(X = 1) = \(\frac{{3 \choose 1}{ 5 \choose 0 }{ 2 \choose 2}}{{10 \choose 3}}}+ \frac{{3 \choose 1}{ 5 \choose 2 }{ 2 \choose 0}}{{10 \choose 3}}} +\frac{{3 \choose 1}{ 5 \choose 1 }{ 2 \choose 1}}{{10 \choose 3}}} = \frac{63}{120}\)
P(X = 2) = \(\frac{{3 \choose 2}{ 5 \choose 1 }{ 2 \choose 0}}{{10 \choose 3}}}+ \frac{{3 \choose 2}{ 5 \choose 0 }{ 2 \choose 1}}{{10 \choose 3}}} = \frac{21}{120}\)
P(X = 3) = \(\frac{{3 \choose 3}}{{10 \choose 3}}} = \frac{1}{120}\)
P(Y = 0) = \(\frac{{3 \choose 1}{ 5 \choose 0 }{ 2 \choose 2}}{{10 \choose 3}}}+ \frac{{3 \choose 2}{ 5 \choose 0 }{ 2 \choose 1}}{{10 \choose 3}}} = \frac{4}{120}\)
P(Y = 1) = \(\frac{{3 \choose 0}{ 5 \choose 1 }{ 2 \choose 2}}{{10 \choose 3}}}+ \frac{{3 \choose 2}{ 5 \choose 1 }{ 2 \choose 0}}{{10 \choose 3}}} +\frac{{3 \choose 1}{ 5 \choose 1 }{ 2 \choose 1}}{{10 \choose 3}}} = \frac{50}{120}\)
P(Y = 2) = \(\frac{{3 \choose 1}{ 5 \choose 2 }{ 2 \choose 0}}{{10 \choose 3}}}+ \frac{{3 \choose 0}{ 5 \choose 2 }{ 2 \choose 1}}{{10 \choose 3}}} = \frac{50}{120}\)
P(Y = 3) = \(\frac{{5 \choose 3}}{{10 \choose 3}}} = \frac{10}{120}\)
E(X) = \(0 \times \frac{25}{120} + 1 \times \frac{63}{120} + 2 \times \frac{21}{120} + 3 \times \frac{1}{120} = \frac{108}{120} = 0.9\)
E(Y) = \(0 \times \frac{4}{120} + 1 \times \frac{50}{120} + 2 \times \frac{50}{120} + 3 \times \frac{10}{120} = \frac{180}{120} = 1.5\)
E(\(X^2\)) = \(0 \times \frac{25}{120} + 1 \times \frac{63}{120} + 4 \times \frac{21}{120} + 9 \times \frac{1}{120} = \frac{156}{120} = 1.3\)
E(\(Y^2\)) = \(0 \times \frac{4}{120} + 1 \times \frac{50}{120} + 4 \times \frac{50}{120} + 9 \times \frac{10}{120} = \frac{340}{120} = 2.833\)
V(X) = \(1.3 - 0.9^2 = 0.49\)
V(Y) = \(2.833 - 1.5^2 = 0.583\)
E(XY) = \(0 \times (\frac{25}{120}\times \frac{4}{100}) + 1 \times (\frac{63}{120} \times \frac{4}{120} + \frac{25}{120} \times \frac{50}{120}) + \\2 \times (\frac{21}{120} \times \frac{4}{120} + \frac{63}{120} \times \frac{50}{120} + \frac{25}{120} \times \frac{50}{120}) + 3 \times (\frac{1}{120} \times \frac{4}{120} + \frac{21}{120} \times \frac{50}{120} + \frac{63}{120} \times \frac{50}{120} \\+ \frac{25}{120} \times \frac{10}{120})\)
\(=\frac{1502}{120^2} + \frac{4484}{120^2} + \frac{4454}{120^2}\\= 1.655\)
Cov(X, Y) = 1.655 - 0.9 \(\times\) 1.5 = 0.305
Corr(X, Y) = \(\frac{ 0.305}{\sqrt{0.49 \times 0.583}}\) = 0.5705
To learn more about probability, refer to the link-
https://brainly.com/question/24756209
#SPJ4
You need 50, 4ounce portions of green beans. Fresh green beans yield 85% edible product after they have been cleaned and trimmed. How many pounds of fresh green beans do you need to purchase? 2. You need ten pounds of fish for stew. The whole fish you are purchasing has a 40% yield after it has been cleaned. How much whole fish do you need to purchase? 3. You are serving a half-pound strip sirloin for a special. Your forecast projects that 60 people will order sirloin, so how many pounds of sirloin should you bring in if, after trimming, you usually have 20% waste?
Answers
1. To have 50, 4-ounce portions of green beans, we need to find how many pounds of fresh green beans should be bought.
Firstly, we'll need to find out how many ounces are needed to have a total of 50 portions of 4-ounces each.
50 portions of 4 ounces each = 50 × 4 = 200 ounces.
To find the total weight in ounces of the green beans that need to be purchased, we divide 200 by 0.85 (as 85% of fresh green beans are edible) as follows:
Total weight in ounces = 200/0.85 = 235.29 ounces.
1 pound is equal to 16 ounces, so to find the total weight in pounds of fresh green beans, we divide 235.29 by 16 as follows:
Total weight in pounds = 235.29/16 = 14.7 pounds.
Therefore, approximately 15 pounds of fresh green beans should be purchased.
2. We need to find out how much whole fish we need to buy to obtain 10 pounds of fish after it has been cleaned (with 40% yield).
We can solve for this using the formula: Yield% = (edible portion ÷ raw portion) × 100.
We can rearrange the formula as: Edible portion = (yield% ÷ 100) × raw portion
We need a 40% yield, so substituting the given values in the formula above, we get:
Edible portion = (40 ÷ 100) × Raw portion
Let's say Raw portion is R. We need 10 pounds of edible portion, so:
10 pounds = (40 ÷ 100) × R10 ÷ (40 ÷ 100) = R25 = R
Therefore, 25 pounds of whole fish should be purchased.
3. We are serving 60 people with half-pound strip sirloin, so we need to find how many pounds of sirloin should be brought in, assuming that 20% of it will be wasted after trimming.
Each serving requires a half-pound, so 60 people need a total of 60 × 0.5 = 30 pounds of sirloin.
To find out the total weight of sirloin that should be brought in, we can use the formula:
Total weight of sirloin = Required weight of sirloin ÷ (1 - Waste%)
Required weight of sirloin = 30 pounds
Waste% = 20% = 0.2
Substituting these values into the formula, we get:
Total weight of sirloin = 30 ÷ (1 - 0.2)= 30 ÷ 0.8= 37.5 pounds.
So, approximately 38 pounds of sirloin should be brought in.
Learn more about purchasing at
https://brainly.com/question/24112214
#SPJ11
Please help me find the equation of the parallel line.
Given: 5x-2y=10, (3,-5)
I know that the formula is y-y1=m(x-x1) but what do I do with the 2y?
Thank you!
Answers
Answer:
mperpendicular = −2/5
Step-by-step explanation:
3 + 11 x 9 - 9 x 10 (8)
Answers
Answer:
-618
Step-by-step explanation:
3 + 11 × 9 - 9 × 10(8)
3 + 11 × 9 - 9 × 80
3 + 99 - 720
102 - 720
- 618
Apply the principle of BODMAS
Step-by-step explanation:
-618
JUST APPLY BODMAS
IT WOULD HELP YOU SOLVE IT WITH EASE
Your client is 34 years old. She wants to begin saving for retirement, with the first payment to come one year from now. She can save $8,000 per year, and you advise her to invest it in the stock market, which you expect to provide an average return of 8% in the future. a. If she follows your advice, how much money will she have at 65? Do not round intermediate calculations. Round your answer to the nearest cent. $ b. How much will she have at 70 ? Do not round intermediate calculations. Round your answer to the nearest cent. $ c. She expects to live for 20 years if she retires at 65 and for 15 years if she retires at 70 . If her investments continue to earn the same rate, how much nearest cent. Annual withdrawals if she retires at 65: $ Annual withdrawals if she retires at 70:$
Answers
If she follows the advice and saves $8,000 per year with an average return of 8%, she will have approximately $861,758.27 at age 65.If she continues saving until age 70, she will have approximately $1,298,093.66. If she retires at 65, she can withdraw approximately $43,087.91 per year for 20 years. If she retires at 70, she can withdraw approximately $86,539.58 per year for 15 years.
To calculate the future value of the savings, we can use the future value of an ordinary annuity formula:
Future Value = Payment * [(1 + interest rate)^n - 1] / interest rate
Where:
Payment = $8,000 (annual savings)
Interest rate = 8% (0.08)
n = number of years
a. Retirement at 65:
n = 65 - 34 = 31 years
Future Value = $8,000 * [(1 + 0.08)^31 - 1] / 0.08 = $861,758.27 (rounded to the nearest cent)
b. Retirement at 70:
n = 70 - 34 = 36 years
Future Value = $8,000 * [(1 + 0.08)^36 - 1] / 0.08 = $1,298,093.66 (rounded to the nearest cent)
c. To calculate the annual withdrawals, we divide the future value by the number of years the client expects to live in retirement.
Retirement at 65:
Annual Withdrawals = Future Value / Number of years in retirement = $861,758.27 / 20 = $43,087.91 (rounded to the nearest cent)
Retirement at 70:
Annual Withdrawals = Future Value / Number of years in retirement = $1,298,093.66 / 15 = $86,539.58 (rounded to the nearest cent)
So, if she retires at 65, she can withdraw approximately $43,087.91 per year, and if she retires at 70, she can withdraw approximately $86,539.58 per year.
Learn more about saving
brainly.com/question/33033886
#SPJ11
\(\huge\bold\red{{HELP}}\)
![[tex]\huge\bold\red{{HELP}}[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/MX7ZmqEyLEA5N4ntG8bfk4UWtZ3sGO1a.jpeg)
Answers
1)
We note that the quadratic can be factored into \((2x-1)(x-1)\).
The quadratic is greater than \(0\) if both of its factors are positive, or they are both negative.
Case: both positive
We need to solve the system of inequalities:
\(2x-1>0\\x-1>0\).
The first inequality gives \(x>\frac{1}{2}\).
The second inequality gives \(x>1\).
Taking the points where the inequalities coincide gives \(x>1\).
(Note: 1 is a root of the quadratic. Coincidence? If not, try and prove it!)
Case: both negative
We need to solve the system of inequalities:
\(2x-1<0\\x-1<0\).
The first inequality gives \(x<\frac{1}{2}\).
The second inequality gives \(x<1\).
Taking the points where the inequalities coincide gives \(x<\frac{1}{2}\).
(Note: \(\frac{1}{2}\) is the other root of the quadratic. Coincidence? If not, try and prove it!)
Taking the union of both cases gives the solution set: \(\boxed{x\in (-\infty, \frac{1}{2}) \cup (1, \infty)}\)
2)
We bring over the \(15\) to get \(x^2-2x-15<0\).
Note that the quadratic factors into \((x-5)(x+3)\).
The quadratic is less than \(0\) if 1 of its factors is negative, but not both.
Case: first factor is negative, second positive
We have that \(x-5<0\) and \(x+3>0\).
We get that \(x<5\) and \(x>-3\), which has the solution set \(-3<x<5\).
Case: second factor is negative, first positive
We have that \(x+3<0\) and \(x-5>0\).
We get that \(x<-3\) and \(x>5\), which has no solutions.
So, the solution set is \(\boxed{x\in (-3, 5)}\)
Solve this equation by elimination method...
2x+7y=-17
3x+10y=-24
Please show work
I will give Brainliest :)
Answers
Answer:
x=2,y=-3
Step-by-step explanation:
detailed explanation showed in the image above


The height of a rider on a Ferris wheel, in metres, can be modelled using the function , where is the angle of rotation. (in calculator use x instead of )
Use a graphing calculator to graph the function.
What is the radius of the Ferris Wheel?
At what height was the rider when the ride began?
How would the function and the graph change if the Ferris wheel turned in the opposite direction?
Answers
Answer:
6
Step-by-step explanation:
At Isaiah's Hats, 70 out of the 100 hats at the store are baseball caps. What percentage of hats at the store are baseball caps?
Answers
Answer:
70%
Step-by-step explanation:
Use the conditional proof for this argument. The proof will take five steps. Choose the answer for line 4, and bear in mind the answer to the previous and next steps. While one or more answers may be justifiable in the proof, only one answer will work when considering the proof as a whole. 1. ~ A / A --> B (The dots between the statement and the justification are there because everything will be too close without them.) Group of answer choices 4. | B ..... 1, 3, DS 4. | ~ ~ ~ A ..... 1, DN 4. | B ..... 1, 3, MP 4. | ~ ~ A ..... 2, DN
Answers
A previous line (not shown here) contains A, and another line (also not shown here) contains A -> B. By using Modus Ponens, we can infer B. the correct answer for line 4 is "| B ..... 1, 3, MP."
Based on the information provided, the correct answer for line 4 in the conditional proof is:
4. | B ..... 1, 3, MP
In the conditional proof, we assume ~A and aim to derive A -> B.
On line 1, ~A is given as the premise.
On line 3, the justification is MP (Modus Ponens). This means that a previous line (not shown here) contains A, and another line (also not shown here) contains A -> B. By using Modus Ponens, we can infer B.
In Modus Ponens (MP), we have two statements: A and A -> B. From these statements, we can infer B.
In the given conditional proof, line 1 states ~A as the premise. Then, on line 3, we have B, which implies that there is a previous line (not shown here) that contains A, and another line (also not shown here) that contains A -> B.
Using Modus Ponens, we can conclude B on line 4.
Therefore, the correct answer for line 4 is "| B ..... 1, 3, MP."
To know more about MP (Modus Ponens) visit:
https://brainly.com/question/27990635
#SPJ11
Longitud de circunferencia si diámetro es 32cm
Answers
Por lo tanto, la longitud de la circunferencia con un diámetro de 32 cm sería aproximadamente 100.53 cm.
How to solve for the circumferenceLa fórmula para calcular la longitud de una circunferencia es:
Longitud = π * Diámetro
En este caso, si el diámetro es de 32 cm, podemos calcular la longitud de la siguiente manera:
Longitud = π * 32 cm
El valor de π (pi) es una constante que representa la relación entre la circunferencia de un círculo y su diámetro. Usualmente, se aproxima a 3.14159.
Por lo tanto, la longitud de la circunferencia sería:
Longitud ≈ 3.14159 * 32 cm
Calculando el resultado:
Longitud ≈ 100.53096 cm
Por lo tanto, la longitud de la circunferencia con un diámetro de 32 cm sería aproximadamente 100.53 cm.
Read moe on circumference here https://brainly.com/question/27447563
#SPJ1
whats x-3y=6 in slope intercept form ?
Answers
Answer:
y = 1/3X - 6
Step-by-step explanation:
Como hago un gráfico de barras
Answers
Answer:
1. Abra Excel. Busque y abra la hoja de cálculo a partir de la cual desea hacer un gráfico de barras.
2. Seleccione todos los datos que desee incluir en el gráfico de barras.
3. Asegúrese de incluir los encabezados de columna y fila, que se convertirán en las etiquetas del gráfico de barras. Si desea etiquetas diferentes, escríbalas en las celdas de encabezado correspondientes.
4. Haga clic en la pestaña Insertar y luego en el botón Insertar columna o gráfico de barras en el grupo Gráficos. Verá muchas opciones cuando seleccione este botón, como columnas 2-D y columnas 3-D, así como barras 2-D y 3-D. Para estos propósitos, estamos seleccionando columnas 2-D.
5. Aparecerá el gráfico. También verá barras horizontales con los nombres de sus encabezados en la parte inferior de su gráfico.
6. A continuación, asigne un nombre a su gráfico. Haga clic en la sección Título del gráfico en la parte superior del gráfico y la sección se vuelve editable.
7. Decida dónde colocar el gráfico de barras. Se puede colocar en una hoja separada o se puede incrustar en la hoja de cálculo. Entonces guárdalo.
8. Si desea eliminar el gráfico y empezar de nuevo, coloque el cursor en el borde del gráfico (aparecerá una ventana emergente que dice "área del gráfico") y presione la tecla Suprimir.
I'll mark brainliest if your right! please help me!!!!

Answers
Answer:
its 3 and 5
Step-by-step explanation:
i know this because i took the quiz and its simple
6. Expand to write an equivalent
expression
-1/6 (-24x + 42y)
O-144x-252y
O 144x + 252y
O-4x-7y
O 4x-7y
Answers
The equivalent expression is 4x-7y. Option D
What are algebraic expressions?These are expressions that are composed of terms, variables, constants, coefficients and factors.
They are also identified with arithmetic operations such as addition, multiplication, division, bracket, parentheses, subtraction, etc.
Equivalent expressions are those expressions that have the same solution but differ in the arrangement of terms.
We have the expression;
-1/6 (-24x + 42y)
multiply the values
24x/6 -42y/6
Divide the values
4x - 7y
Learn about equivalent expressions at: https://brainly.com/question/15775046
#SPJ1
help it’s very urgent please !!!!

Answers
Explanation:
There are eight red flowers
There are ten white flowers
There are five yellow flowers
Add those together.
8+10+5 = 23
Subtract from the total number of flowers which is thirty.
30 - 23 = 7
Answer:
There are 7 blue flowers.
Step-by-step explanation:
Total flowers: 30
Use the chart to find the red, white, and yellow flowers.
Red: 8
White: 10
Yellow: 5
Find the sum of the these three colored flowers:
8 + 10 + 5
23
Find the difference between the total flowers and the sum of the three colored flowers:
30 - 23
7
7 blue flowers
PLEASE HELP FASt, 100 POINTS REWARD
The first quartile of the data set represented by the box plot is [?] The median of the data set is [?]
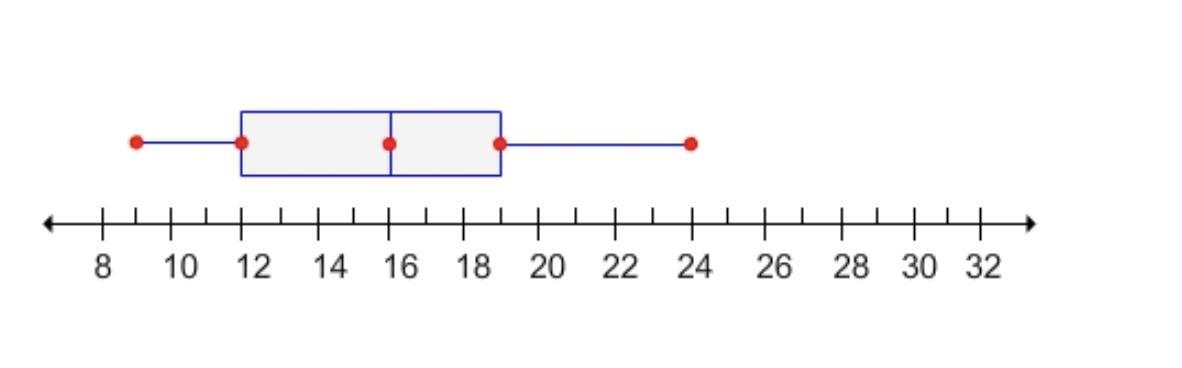
Answers
The first quartile of the data set represented by the box plot is 12.
The median of the data set is 16.
We have,
The box plot is drawn using five summary statistics: minimum, maximum, median, and the first and third quartiles.
The box in the plot represents the middle 50% of the data, with the lower end of the box representing the first quartile (Q1) and the upper end representing the third quartile (Q3).
The median is shown as a line inside the box.
From the box plot,
Median = 16
First quartile = 12
Third quartile = 19
Lowest value = 9
Largest value = 24
Thus,
The first quartile of the data set represented by the box plot is 12
The median of the data set is 16.
Learn more about the quartiles here:
https://brainly.com/question/29204101
#SPJ1
1. what is the smallest number that you know? Do you think it is really the smallest number?
2. what does zero stands for?
3. when you subtract 8 from 10, what is the difference?
4. How about if you subtract 10 from 8? Is there an answer?
5. Are fractions considered as integers?
6. Do you know fractions? Give some examples.
Answers
Answer:
There are numbers that are smaller than zero also ie. - 1,-2,-3,-4,-5 etc.
When u subtract 8 from 10 the answer is 2
And,when u subtract 10 from 8,the answer is -2,so there is a lot of difference.
Part C
What is the equation represented by the graph?

Answers
to get the equation of any straight line, we simply need two points off of it, let's use those two in the picture below
\((\stackrel{x_1}{1}~,~\stackrel{y_1}{8})\qquad (\stackrel{x_2}{3}~,~\stackrel{y_2}{24}) ~\hfill~ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{24}-\stackrel{y1}{8}}}{\underset{\textit{\large run}} {\underset{x_2}{3}-\underset{x_1}{1}}} \implies \cfrac{ 16 }{ 2 } \implies 8\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{8}=\stackrel{m}{ 8}(x-\stackrel{x_1}{1}) \\\\\\ y-8=8x-8\implies {\Large \begin{array}{llll} y=8x \end{array}}\)

Answer:
\(y=8x\)
Step-by-step explanation:
We can see that this line has a constant of proportionality. That is — x is proportional to y and vice versa. This means that the equation for the line's equation will be in the form:
\(y = mx\)
where \(m\) is the ratio of x to y.
This ratio is also known as the line's slope. We can solve for the slope using the equation:
slope = rise / run
slope = \(\Delta\)y / \(\Delta\)x
slope = 8 / 1
slope = 8
\(m=8\)
So, the equation of the line is:
\(y=mx\)
\(\boxed{y=8x}\)
Please help, I don't know how to calculate the things.

Answers
Answer:
30
Step-by-step explanation:
2x+9=3x-21
+21
2x+30=3x
-2x
x=30
Answer:
30
Step-by-step explanation:
the units are unidentified
how to solve (2x+1)^2=(x+2)^2
Answers
Answer:
2
Step-by-step explanation:
2x^2+2=x^2+4
x^2=2
x=2
5. (15 points) Consider the following basis of R 3
B 1
= ⎩
⎨
⎧
⎝
⎛
1
0
6
⎠
⎞
, ⎝
⎛
−1
1
0
⎠
⎞
⎝
⎛
0
1
−3
⎠
⎞
⎭
⎬
⎫
and B 2
= ⎩
⎨
⎧
⎝
⎛
−3
0
1
⎠
⎞
, ⎝
⎛
2
1
−2
⎠
⎞
⎝
⎛
0
0
1
⎠
⎞
⎭
⎬
⎫
. (a) (2 points) Write down the transition matrix B 1
from the basis B 1
to the standard basis. (b) (2 points) Write down the transition matrix B 2
from the basis B 2
to the standard basis. (c) (5 points) Find the transition matrix B from the basis B 2
to the basis B 1
.
Answers
a) The transition matrix from B1 to the standard basis is P = [1 0 -2; 6 1 13; 2 1 5].
b) The transition matrix from B2 to the standard basis is Q = [-2 -1 5; -2 -1 3; -1 0 2].
c) The transition matrix from B2 to B1 is A = [-2 1 -3 5 3 -7; -1 0 1 3 2 5; 0 0 1 -2 -1 2].
a) Basis B1 of R3 is given by
B1 = { (1 0 6), (-1 1 0), (0 1 -3) }.
Write down the transition matrix from B1 to the standard basis. Because the transition matrix is the matrix that changes the standard basis to the basis B1, solve the equation: B1 ∗ P = I, where I is the identity matrix. Solve the following system of equations:
{(1 0 6) (p11 p21 p31)} = {(1 0 0) (1 0 0)}{(−1 1 0) (p12 p22 p32)} = {(0 1 0) (0 1 0)}{(0 1 −3) (p13 p23 p33)} = {(0 0 1) (0 0 1)}
Therefore, the transition matrix from B1 to the standard basis is the matrix P obtained from the solutions of the above system of equations, i.e.,B1 = P-1, where B1 is a matrix having B1 as columns. That is,
P = B1-1 = [1 0 -2; 6 1 13; 2 1 5].
b) Basis B2 of R3 is
B2 = { (-3 0 1), (2 1 -2), (0 0 1) }.
Write down the transition matrix from B2 to the standard basis. Following the same procedure as in part (a), solve the equation B2 ∗ Q = I.
Solving the system of equations given by this equation,
Q = B2-1 = [-2 -1 5; -2 -1 3; -1 0 2].
c) Since B1 and B2 are both bases of R3, each vector in B2 can be expressed as a linear combination of vectors in B1. Let A be the matrix such that A[i] is the i-th vector of B2 expressed as a linear combination of the vectors of B1, i.e.,
A[i]∗B1 = B2[i] for i = 1, 2, 3.
Then the columns of A are the coordinates of the vectors of B2 relative to the basis B1. Hence, the transition matrix from B2 to B1 is given by A. Solve the following system of equations:
{(1 0 6) (a11 a21 a31)} = {(-3 0 1) (a12 a22 a32)}{(-1 1 0) (a13 a23 a33)} = {(2 1 -2) (a14 a24 a34)}{(0 1 −3) (a15 a25 a35)} = {(0 0 1) (a16 a26 a36)}
Solving this system of equations,
A = [-2 1 -3 5 3 -7; -1 0 1 3 2 5; 0 0 1 -2 -1 2].
To learn more about transition matrix,
https://brainly.com/question/15071670
#SPJ11
Which is the polynomial function of lowest degree with rational real coefficients, a leading coefficient of 3 and roots StartRoot 5 EndRoot and 2? f (x) = 3 x cubed minus 6 x squared minus 15 x 30 f (x) = x cubed minus 2 x squared minus 5 x 10 f (x) = 3 x squared minus 21 x 30 f (x) = x squared minus 7 x 10.
Answers
The polynomial function of lowest degree is 3x³ - 6x² - 15x + 30. Then the correct option is A.
What is polynomial?Polynomial is an algebraic expression that consists of variables and coefficients. Variable are called unknown. We can apply arithmetic operations such as addition, subtraction, etc. But not divisible by variable.
The polynomial function of lowest degree with rational real coefficients, a leading coefficient of 3 and ±√5 and 2.
The roots of the polynomial are ±√5 and 2 with a leading coefficient of 3.
Then f(x) will be given as
f(x) = 3(x + √5)(x - √5)(x - 2)
On simplifying, we have
f(x) = 3(x + √5)(x - √5)(x - 2)
f(x) = 3(x² - 5)(x - 2)
f(x) = 3(x³ -2x² - 5x + 10)
f(x) = 3x³ - 6x² - 15x + 30
The polynomial function of lowest degree is 3x³ - 6x² - 15x + 30. Then the correct option is A.
More about the polynomial link is given below.
https://brainly.com/question/17822016
Answer:
the answer is A
Step-by-step explanation:
edge 2022
-6/1 x - 3/5 divided by -0.25
Answers
Answer:
-14.4
Step-by-step explanation:
-6x(-0.6)x(-4)= -14.4
\( - \frac{6(5 - 2x)}{5x} \)
i hope its help
Determine whether or not the indicated set of 3 × 3 matrices is a subspace of M33.
The set of all symmetric 3 × 3 matrices (that is, matrices A = [a such that a; = aj for 1 sis 3, 15j≤3).
Choose the correct answer below.
O A. The set is not a subspace of M33. The set is not closed under addition of its elements.
O B. The set is not a subspace of My. The set does not contain the zero matrix.
O C. The set is a subspace of My. The set contains the zero matrix, the set is closed under matrix addition, and the set is closed under multiplication by other
matrices in the set.
O D. The set is a subspace of M33. The set contains the zero matrix, and the set is closed under the formation of linear combinations of its elements.
Answers
The answer is C. The set of all symmetric 3 × 3 matrices is a subspace of M33.
To determine if a set of matrices is a subspace of M33, we need to check three conditions:
1. The set contains the zero matrix.
2. The set is closed under addition of its elements.
3. The set is closed under multiplication by other matrices in the set.
In this case, the set of all symmetric 3 × 3 matrices does contain the zero matrix (all diagonal entries are zero), and it is also closed under matrix addition (the sum of two symmetric matrices is also symmetric).
To check the third condition, we need to verify that if we multiply any symmetric matrix by another symmetric matrix, the result is also a symmetric matrix. This is indeed true, since the transpose of a product of matrices is the product of their transposes in reverse order: (AB)^T = B^T A^T. For any symmetric matrix A, we have A^T = A, so (AB)^T = B^T A^T = BA, which is also symmetric if B is symmetric.
Therefore, all three conditions are satisfied, and the set of all symmetric 3 × 3 matrices is indeed a subspace of M33.
To know more about matrix visit:
https://brainly.com/question/29995229
#SPJ11
She counted the money and found out she has $14.90 in the jar. How many dimes and quarters does she have?
Answers
Answer:
There're too much possibilities of the answer.
The dot plots show the heights of the players on two basketball teams.
Team A
72 73 74 75 76 77 78 79 80 81 82 83 84
Height (inches)
Team B
72 73 74 75 76 77 78 79 80 81 82 83 84
Height (inches)
Which statement is best supported by these data?
А
The distributions of the data for Team A and Team B are approximately symmetrical.
B
The median height of the players on Team B is less than the median height of the players on Team A.
С
Team B has a greater range in player heights than Team A has.
D
The mode height of the players on Team B is less than the mode height of the players on Team A.
SI
Answers
After answering the presented question, we can conclude that As a graphs result, the best-supported statement by the evidence is A: The data distributions for Team A and Team B are roughly symmetrical.
What is graphs?Mathematicians use graphs to visually display or chart facts or values in order to express them coherently. A graph point usually represents a relationship between two or more things. A graph, a non-linear data structure, is made up of nodes (or vertices) and edges. Glue the nodes, also known as vertices, together. This graph includes V=1, 2, 3, 5, and E=1, 2, 1, 3, 2, 4, and (2.5). (3.5). (4.5). Statistical graphs (bar graphs, pie graphs, line graphs, and so on) are graphical representations of exponential growth. a logarithmic graph shaped like a triangle.
Based on the dot plots, it is clear that both teams have the same set of heights, ranging from 72 to 84 inches. As a result, choices B and C are inappropriate since they entail a comparison of the data from the two teams.
Option A cannot be totally confirmed based on the information provided because dot plots do not provide information on the distribution's shape.
Option D is inappropriate because both teams have the same heights and thus the same mode. As a result, the best-supported statement by the evidence is A: The data distributions for Team A and Team B are roughly symmetrical.
To know more about graphs visit:
https://brainly.com/question/11950136
#SPJ1