A sample of 25 undergraduates reported the following dollar amounts of entertainment expenses last year:
769 691 699 730 711 765 702 718 719 712 768 688 757 695 768 735 709 758 708 693 736 700 687 772 715
Required:
a. What are the range and standard deviation?
b. Use the Empirical Rule to establish an interval which includes about 95 percent of the observations.
Answers
Answer:
\(Range = 85\)
\(\sigma = 28.71\)
\(Interval = [666.78, 781.62]\)
Step-by-step explanation:
Given
The data for 25 undergraduates
Solving (a): Range and Standard deviation
The range is:
\(Range = Highest - Least\)
From the dataset:
\(Highest = 772\)
\(Least = 687\)
So:
\(Range = Highest - Least\)
\(Range = 772-687\)
\(Range = 85\)
The standard deviation is:
\(\sigma = \sqrt{\frac{\sum(x - \bar x)^2}{n}}\)
First, calculate the mean
\(\bar x = \frac{769 +691 +............+715}{25}\)
\(\bar x = \frac{18105}{25}\)
\(\bar x = 724.2\)
So, the standard deviation is:
\(\sigma = \sqrt{\frac{(769-724.2)^2 +(691-724.2)^2 +(699-724.2)^2 +(730-724.2)^2 +............+(715-724.2)^2}{25}}\)
\(\sigma = \sqrt{\frac{20604}{25}}\)
\(\sigma = \sqrt{824.16}\)
\(\sigma = 28.71\)
Solving (b): The interval of the 95% of the observation.
Using the emperical rule, we have:
\(Interval = [\bar x - 2*\sigma, \bar x+ 2*\sigma]\)
\(Interval = [724.2 - 2*28.71, 724.2 + 2*28.71]\)
\(Interval = [666.78, 781.62]\)
Related Questions
An iPad is marked down from $700 to $575. What is the percent markdown of the iPad?
Answers
Solution:
the percent markdown of the iPad is 17.86%
Given:
Original Price = $700
Final price = $575
The markdown is gotten by;
\(Markdown=original~price-final~price\)
\(Markdown=700-575\)
Markdown = $125
Thus, the percent markdown is gotten by;
\(percent~markdown=\frac{markdown}{original~price}~x~ 100\)
percent markdown = \(\frac{125}{700}\) × 100%
percent markdown =\(\frac{12500}{700}\)
percent markdown = 17.857 %
percent markdown ≈ 17.86%
Therefore, the percent markdown of the iPad is 17.86%
Hope this helps!!
If you have any questions please ask.
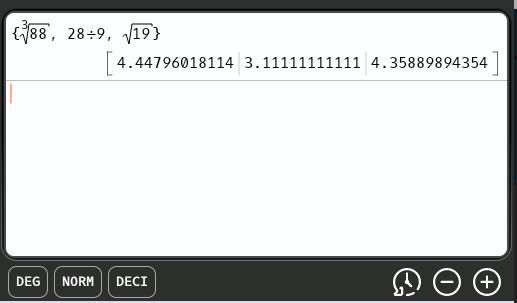
Order cube root of eighty-eight, twenty-eight ninths, square root of nineteen from greatest to least.
cube root of eighty-eight, twenty-eight ninths, square root of nineteen
twenty-eight ninths, square root of nineteen, cube root of eighty-eight
twenty-eight ninths, cube root of eighty-eight, square root of nineteen
cube root of eighty-eight, square root of nineteen, twenty-eight ninths
Answers
Answer:
(a) twenty-eight ninths, square root of nineteen, cube root of eighty-eight
Step-by-step explanation:
When ordering a list of numbers by hand, it is convenient to convert them to the same form. Decimal equivalents are easily found using a calculator.
OrderThe attachment shows the ordering, least to greatest, to be ...
\(\dfrac{28}{9}.\ \sqrt{19},\ \sqrt[3]{88}\)
__
Additional comment
We know that √19 > √16 = 4, and ∛88 > ∛64 = 4, so the fraction 28/9 will be the smallest. That leaves us to compare √19 and ∛88, both of which are near the same value between 4 and 5.
One way to do the comparison is to convert these to values that need to have the same root:
√19 = 19^(1/2) = 19^(3/6) = sixthroot(19³)
∛88 = 88^(1/3) = 88^(2/6) = sixthroot(88²)
The roots will have the same ordering as 19³ and 88².
Of course, these values can be found easily using a calculator, as can the original roots. By hand, we might compute them as ...
19³ = (20 -1)³ = 20³ -3(20²) +3(20) -1 = 8000 -1200 +60 -1 = 6859
88² = (90 -2)² = 90² -2(2)(90) +2² = 8100 -360 +4 = 7744
Then the ordering is ...
28/9 < 19³ < 88² ⇒ 28/9 < √19 < ∛88
Answer:
the ordering is
28/9 < 19³ < 88² ⇒ 28/9 < √19 < ∛88
Step-by-step explanation:
Eugene and Jessica each improved their yards by planting hostas and geraniums. They bought
their supplies from the same store. Eugene spent $150 on 18 hostas and 6 geraniums. Jessica
spent $113 on 7 hostas and 16 geraniums. Find the cost of one hosta and the cost of one
geranium.
Answers
The cost of one hosta is approximately $7 and the cost of one geranium is approximately $4.
To find the cost of one hosta and one geranium, we can set up a system of equations based on the given information.
Let's assume the cost of one hosta is represented by 'h' and the cost of one geranium is represented by 'g'.
From the information given, we can set up the following equations:
Eugene's spending:
18h + 6g = $150
Jessica's spending:
7h + 16g = $113
We can now solve this system of equations to find the values of 'h' and 'g'.
Multiplying the first equation by 2 and the second equation by 3 to eliminate 'g', we get:
36h + 12g = $300
21h + 48g = $339
Now, we can subtract the second equation from the first to eliminate 'h':
(36h + 12g) - (21h + 48g) = $300 - $339
36h - 21h + 12g - 48g = -$39
15h - 36g = -$39
Simplifying further, we have:
15h - 36g = -$39
Now we can solve this equation for 'h' and substitute the value back into any of the original equations to find 'g'.
Let's solve for 'h':
15h = 36g - $39
h = (36g - $39) / 15
Substituting this value of 'h' into Eugene's equation:
18[(36g - $39) / 15] + 6g = $150
(648g - $702) / 15 + 6g = $150
648g - $702 + 90g = $150 * 15
738g - $702 = $2250
738g = $2250 + $702
738g = $2952
g = $2952 / 738
g ≈ $4
Now, substituting the value of 'g' back into Eugene's equation:
18h + 6($4) = $150
18h + $24 = $150
18h = $150 - $24
18h = $126
h = $126 / 18
h ≈ $7
Therefore, the cost of one hosta is approximately $7 and the cost of one geranium is approximately $4.
For such more questions on Cost of Hosta & Geraniums
https://brainly.com/question/14324591
#SPJ8
Solve for x.
6(x - 1) = 9(x + 2)
X = -8
X = -3
X = 3
x = 8
Answers
Answer:x=-8
Step-by-step explanation:
Reread the three paragraphs that begin at the top of page 2 and end on page 3. How does the flashback in these paragraphs advance the plot
Answers
The way the flashback in these paragraphs advance the plot is C. It introduces Evan's motivation for working in the garden with Grandfather.
What is Flashback Narrative?The technique of flashback in storytelling involves interrupting the chronological order of events to depict an earlier event or scene. It uses time travel to furnish the audience with necessary backstory, context, or a deeper understanding of the characters.
The technique of flashbacks is frequently employed as a means of divulging previous occurrences, recollections, or incidents that hold significance to the present narrative being conveyed.
Hence, it can be seen from the given text that the use of flashback helps show the motivation which Evans had for working in the garden with Grandfather
Read more about flashbacks here:
https://brainly.com/question/26179419
#SPJ1

After 3x - y = 7 is put in slope-intercept form, the slope, and intercept are:
m = 3, b = -7
m = -3, b = 7
m = -3, b = -7
m = 3, b = 7
Answers
By converting the equation 3x - y = 7 in the slope-intercept form, the slope, and the intercept will be (A) m = 3, b = -7.
What is the slope-intercept form?When you know the slope of the line to be investigated and the given point is also the y-intercept, you can utilize the slope-intercept formula, y = mx + b. (0, b).
The y value of the y-intercept point is denoted by the symbol b in the formula.
A line's slope and y-intercept are expressed in the following formula: y=mx+b.
The y-intercept, which is usually represented in coordinate form as (0,b), is the point where the line crosses the y-axis.
So, we have the equation:
3x - y = 7
After reading the above-given description about the slope-intercept form, we can tell that in the given equation:
m = 3, b = -7
Therefore, by converting the equation 3x - y = 7 in the slope-intercept form, the slope and the intercept will be (A) m = 3, b = -7.
Know more about the slope-intercept form here:
https://brainly.com/question/22057368
#SPJ1
Complete question:
After 3x - y = 7 is put in slope-intercept form, the slope, and intercept are:
a m = 3, b = -7
b m = -3, b = 7
c m = -3, b = -7
d m = 3, b = 7
Margie volunteered to supply heart-shaped sugar cookies for her third-grade class' Valentine's Day party. Her mom will use premade cookie dough in a tub and buy pink frosting and sprinkles, too. Margie would like to give one cookie to each of her 26 classmates. One tub of cookie dough makes 20 cookies and costs $9.95. The frosting will cover 30 cookies and costs $4.59. The package of sprinkles covers up to cookies 60 and costs $2.29. When Margie's sister, Nicole, hears about the cookies, she asks her mom if they can bake one cookie for each of the students in her class, too. Nicole is in fifth grade and she has 31 students in her class. How much will the ingredients cost for both of the classes?
Answers
Answer: $41.32
Step-by-step explanation:
1. Figure out how many students need cookies.
26 + 31 = 57, 57 students need cookies, thus they need to make at least 57 cookies.
2. Figure out which ingredients are still needed.
One tub of cookie dough makes 20 cookies, so to make 57 cookies, they will need at least three tubs. One frosting tin covers 30 cookies, so to cover 57 cookies, they will need at least two tins. One bag of sprinkles covers 60 cookies, so they will only need one bag, as 60 > 57.
3. Tally up the prices of each ingredient
Price of cookie dough = 9.95, amount of cookie dough needed = 3
9.95 * 3 = 29.85
Price of frosting = $4.59, amount of frosting needed = 2
4.59 * 2 = 9.18
Price of sprinkles = 2.29, amount of sprinkles needed = 1
2.29 * 1 = 2.29
4. Find the sum.
29.85 + 9.18 + 2.29 = 41.32
A) Find an equation for the line perpendicular to the tangent line to the curve y=x^3-4x+6 at the point (2,6)
-The equation is y=
b) What is the smallest slope on the curve? At what point on the curve does the curve have this slope?
-The smallest slope on the curve is
-The curve has the smallest slope at the point
c) Find equations for the tangent lines to the curve at the points where the slope of the curve is 8.
Answers
Answer:
f(x) = x³ - 4x + 6
f'(x) = 3x² - 4
a) f'(2) = 3(2²) - 4 = 12 - 4 = 8
6 = 8(2) + b
6 = 16 + b
b = -10
y = 8x - 10
b) 3x² - 4 = 0
3x² = 4, so x = ±2/√3 = ±(2/3)√3
= ±1.1547
f(-(2/3)√3) = 9.0792
f((2/3)√3) = 2.9208
c) 3x² - 4 = 8
3x² = 12
x² = 4, so x = ±2
f(-2) = (-2)³ - 4(-2) + 6 = -8 + 8 + 6 = 6
6 = -2(8) + b
6 = -16 + b
b = 22
y = 8x + 22
f(2) = 6
y = 8x - 10
The equation perpendicular to the tangent is y = -1/8x + 25/4
-The smallest slope on the curve is 2.92
The curve has the smallest slope at the point (1.15, 2.92)
The equations at tangent points are y = 8x + 16 and y = 8x - 16
Finding the equation perpendicular to the tangentFrom the question, we have the following parameters that can be used in our computation:
y = x³ - 4x + 6
Differentiate
So, we have
f'(x) = 3x² - 4
The point is (2, 6)
So, we have
f'(2) = 3(2)² - 4
f'(2) = 8
The slope of the perpendicular line is
Slope = -1/8
So, we have
y = -1/8(x - 2) + 6
y = -1/8x + 25/4
The smallest slope on the curveWe have
f'(x) = 3x² - 4
Set to 0
3x² - 4 = 0
Solve for x
x = √[4/3]
x = 1.15
So, we have
Smallest slope = (√[4/3])³ - 4(√[4/3]) + 6
Smallest slope = 2.92
So, the smallest slope is 2.92 at (1.15, 2.92)
The equation of the tangent lineHere, we set f'(x) to 8
3x² - 4 = 8
Solve for x
x = ±2
Calculate y at x = ±2
y = (-2)³ - 4(-2) + 6 = 6: (-2, 0)
y = (2)³ - 4(2) + 6 = 6: (2, 0)
The equations at these points are
y = 8x + 16
y = 8x - 16
Read more about tangent lines at
https://brainly.com/question/21595470
#SPJ1
I need help can you help me

Answers
Answer: B.
Step-by-step explanation:
I need help please guys

Answers
Answer:
1053 people
Step-by-step explanation:
2925 x .36 = 1053
Please help me 10 extra points



Answers
The probability of getting hearts or face cards is 25/52.
We know that, Probability of an event = Number of favorable outcomes/Total number of outcomes.
Total number of outcomes = 52 cards
Number of hearts = 13
Number of face cards = 12
Probability getting hearts = 13/52
Probability getting face cards = 12/52
P(Hearts or Face card) = 13/52 + 12/52
= 25/52
Therefore, the probability of getting hearts or face cards is 25/52.
To learn more about the probability visit:
https://brainly.com/question/11234923.
#SPJ1
NO LINKS!! URGENT HELP PLEASE!!!
NOT MULTIPLE CHOICE!!
8. a. Finish the table
b. Name the type of sequence
c. Find the equation for the following sequence

Answers
Answer:
7: 63
8: 73
arithmetic sequence
y = 10x - 7
or f(n) = 10x -7
or
\(a_{n}\) = 3 + (n-1)10
Step-by-step explanation:
the output increases by 10 every time that the input increases by 1. That gives us our common difference or slope. The y intercept is -7. That is the value is you worked backwards until you get to n = 0. The initial value is 3. That is when n is 1.
When n is 3, f(n) is 23
When n is 2, f(n) is 13
When n is 1, f(n) is 3
When n is 0, f(n) is -7
I am not sure if this is clear. I am assuming that you have a lot of knowledge of linear equations and how to write arithmetic sequence. If my explanation is confusing it is me and not you.
Answer:
a. 63,73
b. Arithmetic sequence
c.t(n)=10n-7
Explanation:
a. Here is the completed table:
n | t(n)
4 | 33
5 | 43
6 | 53
7 | 63
8 | 73
b.
The type of sequence is arithmetic.
An arithmetic sequence is a sequence of numbers where the difference between any two consecutive terms is constant.
In this case, the difference between any two consecutive terms is 10.
c.
The equation for the arithmetic sequence is:
t(n)=a+(n-1)d
where:
t(n) is the nth term in the sequencen is the term numberd is the common differencea is the first termFor Question:
d=43-33=10a=?Now
equation becomes:
t(4) = a+(4-1)10
33=a+30
a=33-30
a=3
Now, the Equation becomes
t(n) = 3+(n-1)10
t(n) = 3+10n-10
t(n)=10n-7
A machine cuts 1 & 1/3 Foot long strips of wire. If an 18ft long wire is put into the machine. How many pieces can be cut from the big wire
Answers
Answer:
17 and 5
Step-by-step explanation:
A ball is dropped from a state of rest at time t=0.
The distance traveled after t seconds is s(t)=16t2 ft.
(a) How far does the ball travel during the time interval [6,6.5] ?
Δs= ___ ft
(b) Compute the average velocity over [6,6.5] .
Δs/Δt= ___ ft/sec
(c) Compute the average velocity over time intervals [6, 6.01] , [6, 6.001] , [6, 6.0001] , [5.9999, 6] , [5.999, 6] , [5.99, 6] .Use this to estimate the object's instantaneous velocity at t=6 .
V(6)= ____ ft/sec
Answers
a. s(t) = 4 ft
b. Average velocity = 8 ft/ sec
c. Average velocity = 400 ft/ sec
Average velocity = 4000 ft/sec
Average velocity = 40000 ft/ sec
Average velocity = 400, 000 ft/ sec
Average velocity = 400 ft/ sec
How to determine the valueGiven the expression;
s(t)=16t^2 ft
a. Time interval [6, 6. 5}
Time interval = 6. 5 - 6
Time interval = 0. 5
s(t) = 16 ( 0. 5)^2
s(t) = 16(0. 25)
s(t) = 4 ft
b. Average velocity is expressed as;
Average velocity = velocity/ time taken
Average velocity = 4/ 0. 5 = 8 ft/ sec
c. {6, 6. 01} , Interval = 6. 01 - 6 = 0. 01
Average velocity = 4/ 0. 01 = 400 ft/ sec
[6, 6.001], Interval = 6. 001 - 6 = 0.001
Average velocity = 4/ 0. 001 = 4000 ft/sec
[6, 6.0001], Interval = 6. 0001 - 6 = 0. 0001
Average velocity = 4/ 0. 0001 = 40000 ft/ sec
[5.9999, 6] , Interval = 6 - 5. 9999 = 0. 00001
Average velocity = 4/ 0. 00001 = 400, 000 ft/ sec
[5.99, 6] , Interval = 6 - 5. 99 = 0. 01
Average velocity = 4/ 0. 01 = 400 ft/ sec
Thus, the time interval is estimated by subtracting the initial value from the final value.
Learn more about average velocity here:
https://brainly.com/question/23856383
#SPJ1
Find the measure of one interior angle in each regular polygon. Plz

Answers
Answer:
108°
Step-by-step explanation:
If regular polygon has n sides, then each interior angle = 180° - (360/n)°.
When n = 5, interior angle = 180° - (360/5)° = 108°
1 + tan ( θ ) ÷ 1 − sin ( θ ) = ( tan ( θ ) + csc ( θ ) 2
Answers
Answer:
4655
Step-by-step explanation:
this is not correct question because I know that is omath question
how do i solve for this?

Answers
Step-by-step explanation:
1. KOL = 90
2.KLO = 25
3.NL= 30
4.KL = 17
workings
1.for angle
KOL =90 : the diagonals of rhombus are perpendicular to each other
2. angle LKO + angle KLO + angle KOL =180 : angles of triangle are supplementary(add to 180)
65+ KLO + 90 =180
KLO +155
KLO = 180 - 155
KLO = 25
3. NL = NO + LO: diagonals of the rhombus bisect each other
NL = 15 +15
NL = 30
4. Cos 25 = 15/KL
multiply by KL on both sides
KL × Cos 25 =15
divide by cos 25 on both sides
KL = 17
Fill in the missing reasons to correctly complete the proof.

Answers
For the first question, how do you know that
\(\begin{gathered} \bar{AB}\parallel\bar{CD}; \\ \bar{AD}\parallel\bar{BC} \\ \text{ and these segments are crossed by cross-segment }BD \\ \end{gathered}\)Then, then angles
\(\begin{gathered} \angle ABD \\ \text{and} \\ \angle CDB \end{gathered}\)satisfy the definition of alternate interior angles
The same goes for angles
\(\begin{gathered} \angle ADB \\ \text{and} \\ \angle CBD \end{gathered}\)Therefore, for the first question, the correct answer is Alternate interior angles are congruent.
For the second question, you know that
\(\begin{gathered} \angle ABD\cong\angle CDB \\ \angle ADB\cong\angle CBD \\ \text{and} \\ BD\cong BD \end{gathered}\)And this satisfies the triangle congruence theorem ASA (Angle-side-Angle).
Therefore, for the second question, the correct answer is ASA Triangle Congruence Theorem.
For the third question, since you already know that the triangles ABD and CDB are congruent, then the respective segments that make up the triangles will also be congruent.
Therefore, for the third question, the correct answer is Corresponding parts of congruent triangles are congruent.


Solve for a.
√a-r +m=y

Answers
Answer:
is a mathematics problem and is so easy and square and triangle and rectangle and circle formulas
Step-by-step explanation:
√(a - r) + m = y
√(a - r) = y - m
(a - r) = (y - m)²
a = (y - m)² + r
a = y² - 2my + m² + r.
The answer is the 2nd option.
a clothing business finds there is a linear relationship between the number of shirts, n ,it can sell and the price, p , it can charge per shirt. in particular, historical data shows that 6000 shirts can be sold at a price of $55, while 8000 shirts can be sold at a price of $47. give a linear equation in the form p
Answers
So a linear equation in the form p is P(n) = -$0.004*n + $79.
We have two data points:
6000 shirts can be sold for $55 each.
8000 shirts can be sold for $47 each.
Then we can define the relation:P(n).
Where P is the price, and n is the number of shirts.
Now, we know that we can model this as a linear relationship that passes through the points (6000, $55) and (8000, $47)
A linear relationship can be written as:
y = a*x + b
where a is the slope and b is the y-axis intercept.
For a line that passes through the points (x1, y1) and (x2, y2), the slope can be written as:
a = (y2 - y1)/(x2 - x1).
In this case, the slope is:
a = ($47 - $55)/(8000 - 6000) = -$0.004
Then our equation is:
P(n) = -$0.004*n + b
Now let's find the value of b, we know that:
P(6000) = $55= -$0.004*6000 + b
$55 = -$24 + b
b= $79
Our equation is:
P(n) = -$0.004*n + $79.
The linear equation P(n) = -$0.004*n + $79 has the form p.
To learn more about linear equation visit:
brainly.com/question/29739212
#SPJ4
Figure AAA is a scale image of Figure BBB.

Answers
Answer:
that hard than i though
Step-by-step explanation:
Answer:
x=12
Step-by-step explanation:
Explain in detail using words the step by step process that Maggie took to solve the problem 6.89 x 10^-4 / 7.5 x 10^-6 = .92 x 10^1
Answers
The steps in solving the given expression shows that the result is:
0.92 * 10²
How to use Laws of Exponents?The expression is given as:
6.89 * 10⁻⁴/(7.5 * 10⁻⁶) = 0.92 * 10¹
The steps that Maggie followed are:
Step 1: Rewrite the given expression:
6.89 * 10⁻⁴/(7.5 * 10⁻⁶) = 0.92 * 10¹
Step 2: Divide the coefficients:
The coefficient of the numerator (6.89) is divided by the coefficient of the denominator (7.5) to get:
6.89 / 7.5 = 0.9186667.
Step 3: Divide the powers of 10:
This is done by subtracting the exponent of the denominator 10⁻⁶ from the exponent of the numerator 10⁻⁴ to get: 10²
Step 4: Combine the results:
This gives:
0.9186667 * 10²
Step 5: Simplify the coefficient:
She rounded the coefficient (0.9186667) to two decimal places, resulting in 0.92.
Read more about Laws of Exponents at: https://brainly.com/question/11761858
#SPJ1
1.8 divide by 0.72 explain
Answers
Answer:
0.40
Step-by-step explanation:
Change the divisor 1.8 to a whole number by moving the decimal point 1 places to the right. Then move the decimal point in the dividend the same, 1 places to the right.
We then have the equations:
7.2 ÷ 18 = 0.40
and therefore:
0.72 ÷ 1.8 = 0.40
Both calculated to 2 decimal places.
what the sqare units of a 3 bye 7
Answers
There is 21 square units by 3 and 7. 3 as the column and 7 as a row. You can solve it by multiplying 3 with 7 which gives you 21 or adding 7+7+7 or 3+3+3+3+3+3+3 and all three gives you 21 as the answer. So the square unit of 3 and 7 is 21.
What is a tessellation, how are tessellations used, and what must happen at vertices in order for polygons to tessellate?
Answers
A tessellation is a pattern made by repeating geometric shapes without any gaps or overlaps. These shapes, called tiles or polygons, fit together perfectly to cover a plane or a surface. Tessellations can be found in various forms of art, architecture, and design. They are used to create visually appealing patterns and decorations, as well as to explore mathematical concepts.
Tessellations are utilized in various practical applications, such as tiling floors, walls, and pavements, designing mosaics and quilts, and creating computer graphics and textile patterns. They are also studied in mathematics to understand concepts like symmetry, geometry, and transformations.
For polygons to tessellate, certain conditions must be met at their vertices. At each vertex, the angles formed by the polygons must add up to a whole number of degrees, typically 360 degrees. In other words, the sum of the interior angles of each polygon meeting at a vertex must be a multiple of 360 degrees.
This ensures that the polygons can fit together seamlessly without leaving any gaps or overlaps. Examples of polygons that tessellate include equilateral triangles, squares, and hexagons, as their angles add up to 360 degrees at each vertex.
For more such answers on tessellation
https://brainly.com/question/11869345
#SPJ8
please helpppppp!!!!

Answers
The equation for the polynomial in this problem is given as follows:
\(y = \frac{1}{16}(x^4 - 17x^2 + 16)\)
How to define the functions?We are given the roots for each function, hence the factor theorem is used to define the functions.
The function is defined as a product of it's linear factors, if x = a is a root, then x - a is a linear factor of the function.
The roots for this problem are given as follows:
x = -4.x = -1.x = 1.x = 4.Hence the polynomial is:
y = a(x + 4)(x + 1)(x - 1)(x - 4)
y = a(x² - 16)(x² - 1)
\(y = a(x^4 - 17x^2 + 16)\)
When x = 0, y = 1, hence the leading coefficient a is given as follows:
a = 1/16.
Thus the equation is:
\(y = \frac{1}{16}(x^4 - 17x^2 + 16)\)
More can be learned about the Factor Theorem at brainly.com/question/24729294
#SPJ1
In Jamie's town, there are 42,812 adults and 12,358 children. About how many more adults than children are in Jamie's town?
Answers
Answer:
30454
Step-by-step explanation:
subtraction on a calculator
42812-12358=30454
What is the greatest value? *
Summarize Data
Use the number of text messages Henry sent each day: 6, 12, 2, 6, 3, 4, 2, 5, 6.
Your answer
Answers
Answer:
12
Step-by-step explanation:
Woah that's a lot of points! Well in the list 12 is the largest! I think it may be wrong because it's pretty simple but yeah!
can someone help me with this

Answers
The sine equation for the object's height is given as follows:
d = -5sin(0.24t).
How to define the sine function?The standard definition of the sine function is given as follows:
y = Asin(Bx) + C.
The parameters are given as follows:
A: amplitude.B: the period is 2π/B.C: vertical shift.The amplitude for this problem is of 5 inches, hence:
A = 5.
The period is of 1.5 seconds, hence the coefficient B is given as follows:
2π/B = 1.5
B = 1.5/2π
B = 0.24.
The function starts moving down, hence it is negative, so:
d = -5sin(0.24t).
More can be learned about trigonometric functions at brainly.com/question/21558626
#SPJ1
PLEASE HELP ME QUICK!!!

Answers
Answer:
Option D. \(g(x)=5(0.8)^{x}+2\)
Step-by-step explanation:
Main concepts
Concept 1: identifying horizontal asymptote
Concept 2: assuring decreasing exponential function
Concept 1. identifying horizontal asymptote
Any exponential function of the form \(y=a*b^x\) has a horizontal asymptote on the x-axis. A constant (positive or negative) added to the end of the exponential expression will shift the graph of the exponential function up (if positive) or down (if negative) the number of units equal to the magnitude of the number. Since the original function f(x) has a "+2" at the end, it has been shifted up 2 units. Thus, we can eliminate answers A and C from feasible answers since they each shift the exponential function up 3 units, not 2.
Concept 2. assuring decreasing exponential function
Exponential functions of the form \(y=a*b^x\) increase or decrease based on the value of "b".
If "b" is between 0 and 1 (a "small" number), the function will decrease.If "b" is larger than 1 (a "big" number), the function will increase.Observe that the graph of the function f(x) is decreasing, and the value of b=0.5.
To ensure that g(x) also decreases, the b-value must be between 0 and 1, which eliminates option B.
Option D is the correct answer because the value of "b" is between 0 and 1 (making the graph of the function a decreasing exponential), and the number added at the end is "+2", causing the horizontal asymptote to be at a height of positive 2.