A salesperson is paid a flat rate plus a fixed percentage of her sales. Last month, she sold $16,000 worth of goods and was paid $1,600. Two months ago, she had $12,000 in sales and was paid $1,400. This month she sold $11,000 worth of goods. How much will she be paid?
Answers
Answer:
She will be paid $1,350
Step-by-step explanation:
Linear Modeling
Some events can be modeled as linear functions. If we are in a situation where a linear model is suitable, then we need two sample points to make the model and predict unknown behaviors.
The linear function can be expressed in the slope-intercept format:
y=mx+b, where m and b are constants.
The payments for a salesperson will be linearly modeled. There are two known points: When the sales were $16,000, the payment was $1,600. This makes the point (16,000;1,600).
We also know when the sales were $12,000, the payment was $1,400. The point is (12,000;1,400)
Let's use the points to find the values of m and b.
Using (16,000;1,600):
1,600=m*16,000+b
Using (12,000;1,400):
1,400=m*12,000+b
Subtracting both equations:
200=16,000m-12,000m
200=4,000m
Solving:
m=200/4,000=0.05
Using the first equation and the value of m:
1,600=0.05*16,000+b
1,600=800+b
Solving:
b=800
The equation is now complete:
y=0.05x+800
She sold $11,000 this month, so the payment is:
\(y=0.05\cdot 11,000+800\)
Y=550+800=1,350
She will be paid $1,350
Answer:
1350
Step-by-step explanation:
(Note: this method is not the best to use in future problems, please refer to the other answer if you want something better to use.)
16,000-12,000=4,000
1,600-1,400=200
To find the rate of change in 1000s:
200/4 = 50
Essentially this means the rise is 50 and the run is 1000, so, just remove $50 from the payment from 2 months ago to find your answer
Related Questions
Seven years ago, Grogg's dad was 6 times as old as Grogg, and 3 years ago, his dad was 4 times as old as Grogg. How old is Grogg's dad currently?
Answers
Answer:
Grogg's dad is 22
Step-by-step explanation:
Let D = dad's current age
Let g = Grogg's current age
6(d - 7) = g - 7 → 6d - 42 = g - 7 → 6d -35 = g
4(d - 3) = g - 3 → 4d -12 = g - 3 → 4d -9 = g
Set the two equations equal to each other and solve for d
6d - 35 = 4d - 9 Subtract 4d from both sides
2d -35 = -9 Add 35 to both sides
2d = 44 Divide both sides by 2
d = 22
Helping in the name of Jesus.
Answer:
Step-by-step explanation:
d = current dad age
g = current grogg age
d-7 = 6(g-7)
d-3 = 4(g-3)
Let's solve the first equation first:
Add 7 to both sides: d - 7 +7 = 6g - 42 + 7 so d = 6g - 35
Substitude d = 6g - 35 for d in d - 3 = 4g - 12
(6g-35)-3 = 4g-12 = 6g-38 = 4g-12
Subtract 4g from both sides: 2g - 38 = -12
Add 38 to both sides: 2g = 26
Easy: g = 13
And now substitude g in for any equations.
d-3 = 52-12
d = 43
Use the table to answer the following questions x 0 3 6 9 12 15 18 21 24 27 g ( x ) 24 12 24 6 21 18 27 3 6 27 Evaluate g ( 9 ) : g ( 9 ) = For what value(s) of x does g ( x ) = 21 ? x =
Answers
The value of g(9) is 6 and the value of x which g(x) = 21 is12
How to interpret the function values from the table?The table of values is given as
x 0 3 6 9 12 15 18 21 24 27
g(x) 24 12 24 6 21 18 27 3 6 27
The value of g(9):
From the table, we can see that
When x = 9, the value of the function is
f(x) = 6
This means tat
g(9) = 6
The value of x at g(x) = 21:
From the table, we can see that
When g(x) = 21, the value of the x is
x = 12
This means tat
g(12) = 21
Hence, the value of g(9) is 6 and the value of x which g(x) = 21 is12
Read more about functions at
https://brainly.com/question/1415456
#SPJ1
An arrow is shot from 3 ft above the top of a hill with a vertical upward velocity of 108 ft/s. If it strikes the plain below after 9.5 s, how high is the hill?
If the arrow is launched at t0, then write an equation describing velocity as a function of time?
Answers
The height of the hill is approximately 25.73 ft. Where v0 is the initial velocity (108 ft/s), g is the acceleration due to gravity \((-32.2 ft/s^2)\),
To find the height of the hill, we can use the formula for the vertical position of an object under constant acceleration:
h = h0 + v0t + 1/2at^2
where h is the final height, h0 is the initial height, v0 is the initial velocity, t is the time, and a is the acceleration due to gravity (-32.2 ft/s^2).
In this case, we are given that the initial height h0 is 3 ft, the initial velocity v0 is 108 ft/s, and the time t is 9.5 s. We want to find the height of the hill, which we can denote as h_hill. The final height is the height of the plain, which we can denote as h_plain and assume is zero.
At the highest point of its trajectory, the arrow will have zero vertical velocity, since it will have stopped rising and just started to fall. So we can set the velocity to zero and solve for the time it takes for that to occur. Using the formula for velocity under constant acceleration:
v = v0 + at
we can solve for t when v = 0, h0 = 3 ft, v0 = 108 ft/s, and a = -32.2 ft/s^2:
0 = 108 - 32.2t
t = 108/32.2 ≈ 3.35 s
Thus, it takes the arrow approximately 3.35 s to reach the top of its trajectory.
Using the formula for the height of an object at a given time, we can find the height of the hill by subtracting the height of the arrow at the top of its trajectory from the initial height:
h_hill = h0 + v0t + 1/2at^2 - h_top
where h_top is the height of the arrow at the top of its trajectory. We can find h_top using the formula for the height of an object at the maximum height of its trajectory:
h_top = h0 + v0^2/2a
Plugging in the given values, we get:
h_top = 3 + (108^2)/(2*(-32.2)) ≈ 196.78 ft
Plugging this into the first equation, we get:
h_hill = 3 + 108(3.35) + 1/2(-32.2)(3.35)^2 - 196.78
h_hill ≈ 25.73 ft
If the arrow is launched at t0, the equation describing velocity as a function of time would be:
v(t) = v0 - gt
For such more questions on velocity
https://brainly.com/question/25749514
#SPJ8
PLS HELP !!!! WILL MARK BRAINLIEST !!
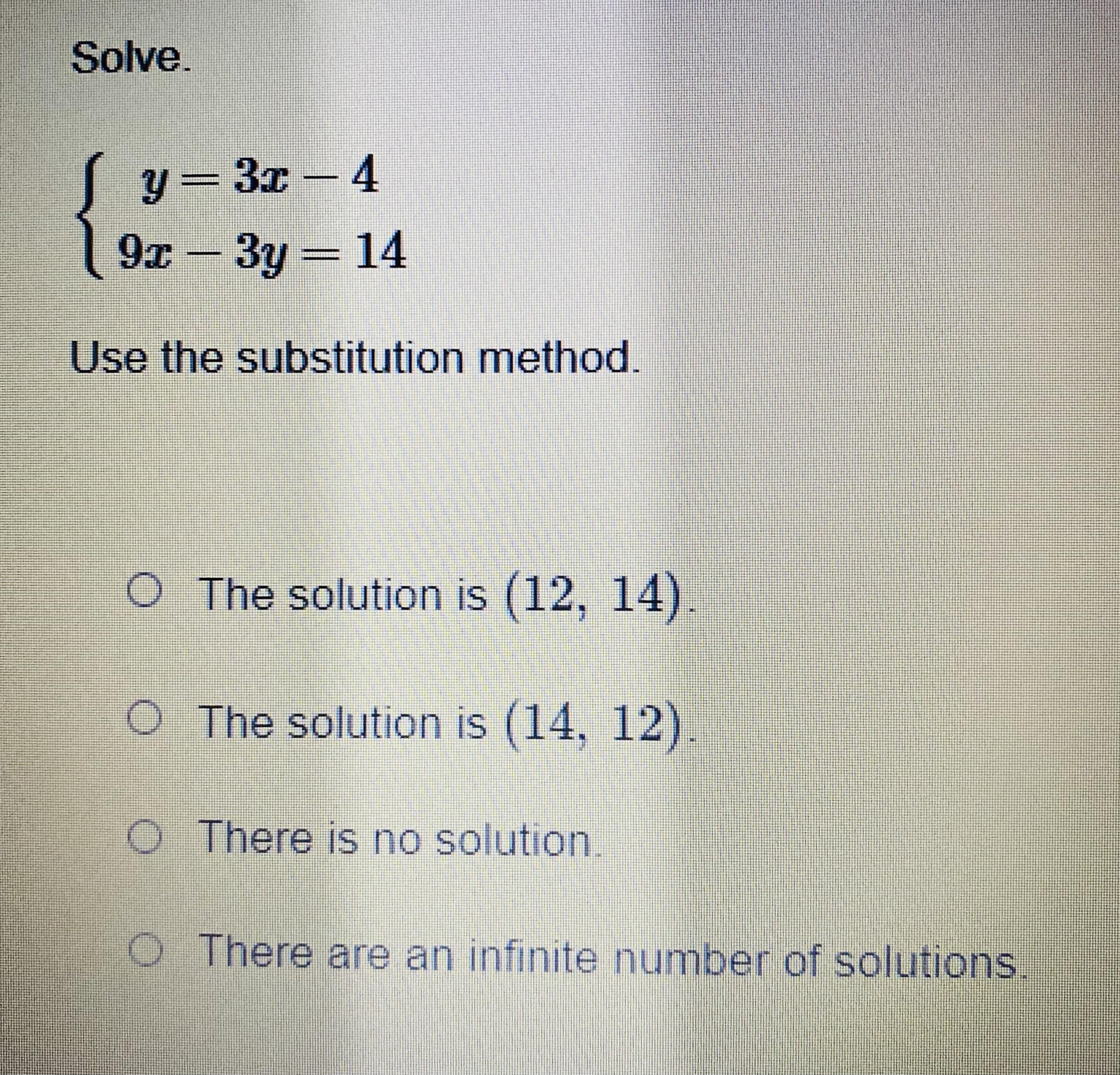
Answers
Answer: Choice C) no solution
=============================================================
Explanation:
The first equation says that y and 3x-4 are the same thing.
So we can replace every copy of "y" in the second equation with "3x-4" like so
9x - 3y = 14
9x - 3(3x-4) = 14
9x - 9x + 12 = 14
0x + 12 = 14
0 + 12 = 14
12 = 14
The last equation is false because we get different values on either side. Because the last equation is false, it means the equation 9x-3y = 14 is false when y = 3x-4.
In short, the overall systems of equations is inconsistent and that leads to no solution (choice C).
If you were to graph each equation, you should find that both lines are parallel. Parallel lines never intersect. The solution is the intersection point of any graphed system.
Answer:
there is no solution to this problem
Step-by-step explanation:
I hope this helps
For any unit vectors v and w, find the dot products (actual numbers) of
(a) v and -v (b) v + w and v – w (c) v – 2w and v + 2w
Answers
a) The dot product of v and -v is -1.
b) The dot product of v + w and v – w is 2v.w
c) The dot product of v – 2w and v + 2w is 4||w||^2 - 4v.w
(a) For any unit vector v, the dot product of v and -v can be found as follows:
v · -v = ||v||||-v||cos(θ) = ||v||||v||cos(180°) = -||v||^2 = -1, where ||v|| represents the magnitude of the vector v and θ is the angle between the vectors.
Since v and -v are unit vectors, their magnitudes are equal to 1, so ||v||^2 = 1. Thus, the dot product of v and -v is -1.
(b) For any unit vectors v and w, the dot product of v + w and v – w can be found as follows:
(v + w) · (v – w) = ||v + w||||v – w||cos(θ) = (||v||||v|| + 2v · w + ||w||||w||)cos(θ) = 2v · w
where θ is the angle between the vectors v + w and v – w, and v · w is the dot product of v and w.
(c) For any unit vectors v and w, the dot product of v – 2w and v + 2w can be found as follows:
(v – 2w) · (v + 2w) = ||v – 2w||||v + 2w||cos(θ) = (||v||||v|| + 4||w||||w|| - 4v · w)cos(θ) = 4||w||^2 - 4v · w
where θ is the angle between the vectors v – 2w and v + 2w, and v · w is the dot product of v and w.
To learn more about vectors click on,
https://brainly.com/question/14376687
#SPJ4
in the figure below the areas of rectangles A, B, and C are 12, 24, and 40, respectively. The find the area of the rectangle d
Answers
Answer:
20?
Step-by-step explanation:
Use the quadratic formula to find the exact solutions of 3x2 − 6x + 2 = 0.
a. negative 1 plus or minus the square root of 3 divided by 3
b. 1 plus or minus the square root of 3 divided by 3
c. negative 1 plus or minus the square root of 15 divided by 3
d. 1 plus or minus the square root of 15 divided by 3

Answers
The exact solutions of the qudratic equation 3x^2 - 6x + 2 = 0 are:
a. negative 1 plus or minus the square root of 3 divided by
3 (x = (-1 ± √3) / 3) .So, option a is the correct answer.
To find the solutions of the quadratic equation 3x^2 - 6x + 2 = 0, we can use the quadratic formula, which states that for an equation of the form ax^2 + bx + c = 0, the solutions are given by:
x = (-b ± √(b^2 - 4ac)) / (2a)
In this case, a = 3, b = -6, and c = 2. Substituting these values into the formula, we have:
x = (-(-6) ± √((-6)^2 - 4(3)(2))) / (2(3))
x = (6 ± √(36 - 24)) / 6
x = (6 ± √12) / 6
x = (6 ± 2√3) / 6
x = (3 ± √3) / 3
Therefore, the exact solutions of the equation 3x^2 - 6x + 2 = 0 are:
a. negative 1 plus or minus the square root of 3 divided by 3 (x = (-1 ± √3) / 3)
So, option a is the correct answer.
To learn more about : quadratic
https://brainly.com/question/1214333
#SPJ11

Javier bought a painting for
$
150
$150dollar sign, 150. Each year, the painting's value increases by a factor of
1.15
1.151, point, 15.
Which expression gives the painting's value after
7
77 years?
Choose 1 answer:
Choose 1 answer:
(Choice A)
(
150
⋅
1.15
)
7
(150⋅1.15)
7
left parenthesis, 150, dot, 1, point, 15, right parenthesis, start superscript, 7, end superscript
A
(
150
⋅
1.15
)
7
(150⋅1.15)
7
left parenthesis, 150, dot, 1, point, 15, right parenthesis, start superscript, 7, end superscript
(Choice B)
150
⋅
1.1
5
7
150⋅1.15
7
150, dot, 1, point, 15, start superscript, 7, end superscript
B
150
⋅
1.1
5
7
150⋅1.15
7
150, dot, 1, point, 15, start superscript, 7, end superscript
(Choice C)
(
150
+
1.15
)
⋅
7
(150+1.15)⋅7left parenthesis, 150, plus, 1, point, 15, right parenthesis, dot, 7
C
(
150
+
1.15
)
⋅
7
(150+1.15)⋅7left parenthesis, 150, plus, 1, point, 15, right parenthesis, dot, 7
(Choice D)
150
+
1.15
⋅
7
150+1.15⋅7150, plus, 1, point, 15, dot, 7
D
150
+
1.15
⋅
7
150+1.15⋅7
Answers
The correct expression is \($(150 \cdot 1.15)^7$\) (Choice A).
The problem states that the painting's value increases by a factor of 1.15 each year. This means that the value at the end of each year is 1.15 times the value at the beginning of the year. Therefore, after one year, the value of the painting is\($150 \cdot 1.15 = 172.50$\).
To find the value after 7 years, we need to multiply the value of the painting each year by 1.15 a total of 7 times. This can be represented mathematically as \($(150 \cdot 1.15)^7$\). This expression is equal to the starting value of the painting, 150, multiplied by 1.15$ raised to the 7th power, which represents the 7 years of appreciation.
If we were to choose expression B, it would give an incorrect result because it uses a value of 1.1 instead of 1.15 to represent the yearly increase in value.
Expressions C and D are also incorrect because they are not taking into account the compounding effect of the yearly increase. Expression C adds the initial value and the total years together, and expression D adds the initial value to the yearly increase multiplied by 7, neither of which correctly reflects the exponential growth of the painting's value.
For such more questions on expression
https://brainly.com/question/1859113
#SPJ8
I need help with this question. Thank you!

Answers
Answer:
gradient is the same as slope The gradient or slope of line A = 3/1 or 3
The gradient of line B is -4/1 or -4
gradient or slope = rise over run = y/x.
if the line goes up from the left to the right, The slope is positive.
if the line goes down from the left to the right, The slope is negative

What is the meaning of "\( \varphi (x,y)\) be \( y\wedge \phi (x)\) "?
![What is the meaning of "[tex] \varphi (x,y)[/tex] be [tex] y\wedge \phi (x)[/tex] "?](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/qBCO5ypO9m13MpdV66LMvZB6FUp8SIQM.png)
Answers
The reasoning presented lacks explicit explanations and logical connections between the steps, making it difficult to fully understand the intended proof strategy.
The given proof aims to show that the Separation Axioms can be derived from the Replacement Schema using a particular construction involving a formula p(x, y). Let's analyze the proof step by step:
Define the formula p(x, y) as x = yo(x).
This formula states that for each x, y pair, x is equal to the unique object y such that y is obtained by applying the operation o to x.
Define the set F as {(x, x) (x)}.
This set F contains pairs (x, x) where x is the unique object obtained by applying the operation (x) to x.
Claim: F(X) = {y (x = X)p(x, y)} = {y: (x = X)x = y^o(x)} = {x: (3x € X)o(x)} = {x X: (x)}.
This claim asserts that F(X) is equivalent to {y (x = X)p(x, y)}, which is further equivalent to {y: (x = X)x = y^o(x)}, and so on.
The proof states that since (x, y) satisfies the functional formula VaVyVz(p(x, y)^(x, z) y = z), it follows that (x, y) is a functional formula.This step emphasizes that the formula p(x, y) satisfies certain properties that make it a functional formula, which is relevant for the subsequent deductions.
Finally, the proof concludes that the Separation Axioms follow from the Replacement Schema, based on the previous steps.
For more such questions on explicit
https://brainly.com/question/30394385
#SPJ8
1383400691
Find the experimental probability that 3 of 4
children in a family are boys.
The problem has been simulated by tossing 4
coins (one to represent each child). Let "heads"
represent a boy and "tails" represent a girl. A
sample of 20 coin tosses is shown.
HTHH HTTH TTTT THTT HTHT
HHTT HHHT THHT HTTH TTHH
HTTT HTHT TTHH THTH HTHH
TTHT HTTT HTHT HHHT HHHH
Experimental Probability
Answers
HTHH, HTTH, TTHH, THTH, HTHH, and HTHH
Therefore, the experimental probability of getting 3 boys out of 4 children in a family is
6/20 or 0.3 or 30%.
50 points for 3 questions. solve and explain please.



Answers
(1) The value of x is determined as 16.8.
(2) The measure of length VX is calculated as 4.1.
(3) The measure of angle UWV is 69.5⁰.
What is the value of the missing lengths of the triangle?
The value of the missing lengths of the triangle is calculated by applying the following formula;
(1) For the two similar triangles, the value of x is calculated as follows;
20 / (28 - x) = 30 / x
20x = 30 (28 - x )
20x = 840 - 30x
20x + 30x = 840
50x = 840
x = 840 / 50
x = 16.8
(2) The measure of length VX is calculated by applying trig ratios.
tan 63 = 8 / VX
VX = 8 / tan 63
VX = 4.1
(3) The measure of angle UWV is calculated as follows;
angle T = 360 - (94 + 127) = 139
angle UWV = ¹/₂ x 139 (angle at circumference is half of angle at center)
angle UWV = 69.5⁰
Learn more about trig ratios here: https://brainly.com/question/10417664
#SPJ1
A string passing over a smooth pulley carries a stone at one end. While its other end is attached to a vibrating tuning fork and the string vibrates forming 8 loops. When the stone is immersed in water 10 loops are formed. The specific gravity of the stone is close to
A) 1.8
B) 4.2
C) 2.8
D) 3.2
Answers
Answer:
correct option is C) 2.8
Step-by-step explanation:
given data
string vibrates form = 8 loops
in water loop formed = 10 loops
solution
we consider mass of stone = m
string length = l
frequency of tuning = f
volume = v
density of stone = \(\rho\)
case (1)
when 8 loop form with 2 adjacent node is \(\frac{\lambda }{2}\)
so here
\(l = \frac{8 \lambda _1}{2}\) ..............1
\(l = 4 \lambda_1\\\\\lambda_1 = \frac{l}{4}\)
and we know velocity is express as
velocity = frequency × wavelength .....................2
\(\sqrt{\frac{Tension}{mass\ per\ unit \length }}\) = f × \(\lambda_1\)
here tension = mg
so
\(\sqrt{\frac{mg}{\mu}}\) = f × \(\lambda_1\) ..........................3
and
case (2)
when 8 loop form with 2 adjacent node is \(\frac{\lambda }{2}\)
\(l = \frac{10 \lambda _1}{2}\) ..............4
\(l = 5 \lambda_1\\\\\lambda_1 = \frac{l}{5}\)
when block is immersed
equilibrium eq will be
Tenion + force of buoyancy = mg
T + v × \(\rho\) × g = mg
and
T = v × \(\rho\) - v × \(\rho\) × g
from equation 2
f × \(\lambda_2\) = f × \(\frac{1}{5}\)
\(\sqrt{\frac{v\rho _{stone} g - v\rho _{water} g}{\mu}} = f \times \frac{1}{5}\) .......................5
now we divide eq 5 by the eq 3
\(\sqrt{\frac{vg (\rho _{stone} - \rho _{water})}{\mu vg \times \rho _{stone}}} = \frac{fl}{5} \times \frac{4}{fl}\)
solve irt we get
\(1 - \frac{\rho _{stone}}{\rho _{water}} = \frac{16}{25}\)
so
relative density \(\frac{\rho _{stone}}{\rho _{water}} = \frac{25}{9}\)
relative density = 2.78 ≈ 2.8
so correct option is C) 2.8
PLEASE HELP !! ILL GIVE BRAINLIEST !!

Answers
Answer:
<YXZ and <TUS
Step-by-step explanation:
An exterior angle is found outside the parallel line. When you have two exterior angles that are opposite each other along the transversal, they are referred to as alternate exterior angles.
Therefore, the only pair of angles from the given options that flare alternate exterior angles are:
<YXZ and <TUS
Please Help me solve this equation

Answers
What are vertices of the conic 16x² - 25y² = 400 ?
Answers
Answer:
(-5, 0) and (5, 0)
Step-by-step explanation:
This equation fits the form for a hyperbola with x-intercepts. The standard form for such an equation is
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)
To get the equation in the question into this standard form, divide each term by 400.
\(\frac{16x^2}{400}-\frac{25y^2}{400}=\frac{400}{400}\\\frac{x^2}{25}-\frac{y^2}{16}=1\)
To find the x-intercepts, make y = 0.
\(\frac{x^2}{25}=1\\x^2=25\\x=\pm 5\)
The vertices are located at the points (-5, 0) and (5, 0).
Note: There are no y-intercepts; making x = 0 produces no real solutions for y.
Find the area of the semicircle

Answers
Area of Semicircle = 1/2 (π r2)
Step-by-step explanation:
area of a semicircle is half of the area of the circle. As the area of a circle is πr2. So, the area of a semicircle is 1/2(πr2 ), where r is the radius The value of π is 3.14 or 22/7.
Answer:
Area of the semicircle = 1.57 square feet
Step-by-step explanation:
radio = 2/2 = 1 ft.
\(A_{s} =\frac{\pi r^{2} }{2} =\frac{\pi (1)^{2} }{2} =\frac{\pi }{2}\)
\(A_{s} =1.57sq.ft\)
Hope this helps
what is the slope of a line perpendicular to the line those equations is 12 x - 2 y=24 fully reduced your answer
Answers
Given the line 12x - 2y = 24
At first, make the line on the form of slope intercept form
So,
12x - 2y = 24
-2y = -12x + 24
Divide all terms by -2
y = 6x - 12
So, it will be similar to the general form y = mx + b
Where m is the slope and b is y-intercept
so, the slope = m = 6
So, the slope of the line perpendicular to the given line will be -1/6
Because the product of the slopes of the perpendicular line = -1
So, the answer is
Create a dot plot of the data shown below.
20, 21, 21, 25, 20, 23, 27, 23, 24, 25, 26, 24, 23, 22, 24
Which measure of center would best describe a typical
value of the data set? Why?
would be best,
The mean
because the data distribution is
V nearly symmetrical
Intro
Click or tap the number line to add a dot.
20 21
22
23 24 25 26 27 28 29
Reset
Answers
Based on the data, the mean would be the best measure of center to describe a typical value in the data set.
How to create a dot plot with the given data?To create a dot plot, we can list the numbers in order and place a dot above the corresponding value on the number line.
20 ••
21 ••
22 •
23 ••••
24 •••••
25 ••
26 ••
27 •
The dot plot shows a relatively symmetric distribution of the data, with the majority of values clustered around the middle. Therefore, the mean would be a good measure of center to describe a typical value of the data set.
Learn more about dots plot in: https://brainly.com/question/22746300
#SPJ1

Assume the weight of a randomly chosen American passenger car is a uniformly distributed random variable ranging from 2,674 pounds to 4,089 pounds. (a) What is the mean weight of a randomly chosen vehicle? (Round your answer to the nearest whole number.) Mean weight 3382 (b) What is the standard deviation of a randomly chosen vehicle? (Round your answer to 4 decimal places.) Standard deviation 408.475 (c) What is the probability that a vehicle will weigh less than 2,961 pounds? (Round your answer to 4 decimal places.) Less than 2,961 pounds 33815 (d) What is the probability that a vehicle will weigh more than 3,814 pounds? (Round your answer to 4 decimal places.) More than 3,814 pounds - (e) What is the probability that a vehicle will weigh between 2,961 and 3,814 pounds? (Round your answer to 4 decimal places.) Between 2,961 and 3,814 pounds
Answers
We must determine the percentage of the total area under the uniform distribution curve to the right of 3,814 pounds in order to determine the probability that a car will weigh more than 3,814 pounds.
What is probability?Mathematicians use probability theory to determine the likelihood that an event will occur or a statement is accurate. A probability of essentially 0 shows how likely an occurrence appears to occur, while a risk is a number between 0 and 1, where 1 implies certainty.
(a) The average of the vehicle's lowest and highest weights, or (2,674 + 4,089) / 2, equals 3,382 pounds, is the mean weight of the vehicle. The mean weight is 3,382 when rounded to the closest whole number.
(b) The formula for calculating the standard deviation of a uniform distribution is (b - a) / 12, where a denotes the lowest value and b denotes the maximum value. We arrive at (4,089 - 2,674) / 12 = 408.4751 after substituting the numbers. The standard variation, rounded to four decimal places, is 408.475.
(c) We must determine the percentage of the total area under the uniform distribution curve that lies to the left of 2,961 pounds in order to determine the likelihood that a car will weigh less than 2,961 pounds. (2,961 - 2,674) / (4,089 - 2,674) = 0.33815 is the formula for this region. The chance, rounded to four decimal places, is 0.3381.
(d) We must determine the percentage of the total area under the uniform distribution curve to the right of 3,814 pounds in order to determine the likelihood that a car will weigh more than 3,814 pounds. (4,089 - 3,814) / (4,089 - 2,674) = 0.2904 gives the area of this triangle. The chance, rounded to four decimal places, is 0.2904.
To know more about probability visit:
https://brainly.com/question/11234923
#SPJ1
Please help ASAP! If you know or have the answers to this sheet, please post a picture of it in the comments. Thank you!

Answers
Answer:
Question 1 read explanation. Question 2 it's c= 5. Question 3 it's 5 miles. Question4 it's
Step-by-step explanation:
For question 1 it's just asking you to make a right triangle with the segment as the hypotenuse. To do that make a dot on (5,1) and draw the triangle. A hypotenuse is the longest side of a right triangle, opposite the right angle.
For question 2 you just get the units of the triangle. The hypotenuse is always c (the segment). However, it's difficult to find c by just looking at the graph. That's why you plug in the other sides a = 3 and b = 4 (doesn't matter which way) to find c. So, you plug in 3^2 + 4^2 = c^2. This will give 9 + 16 = c^2, which is 25 = c^2. We need c not c^2! That means we square 25 to get 5. c = 5!
For question 3, you use the answer from question 2 I believe, so it's 5 miles.
For question 4, it's the same as question 1 so if it helps you make a visual on paper. Draw those two dots and to make a right triangle you'll also need the point (1,1). Find the units 8^2 + 10^2 = c^2. c = 2root41.
a jar contains 5 blue marbles, 7 yellow marble, and 8 green marbles. what is the probability of randomly choosing a blue marble, not replacing it, and then choosing a green marble
Answers
Answer:
10.526% or 0.10526
Step-by-step explanation:
The probability of choosing a blue marble would be 5/20, or 0.25 and then the probability of choosing a green marble next would be 8/19, or about 0.421. Multiply these probabilities together to get your answer.
Hope this helps:)
a tee junction occurs when a connection meets an existing pipe of header at what angle? A 180 degree, B 30 degree, C. 90 degree, D.45 degree
Answers
Tee welding joints are formed when two members intersect at a 90-degree angle that makes the edges come together in the center of a plate or component
Which is the first step you should do when solving the equation below.
3x^2-4= 71
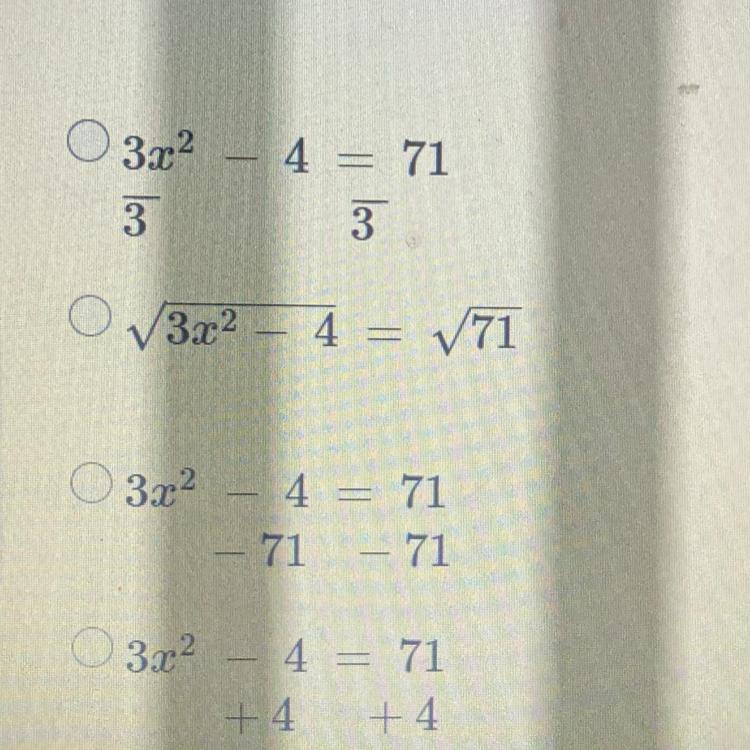
Answers
Answer:
the last option
Step-by-step explanation:
please help me with my online classwork!

Answers
Answer:
840 cm²---------------------------
There are two triangular faces with base of 16 cm and height of 15 cm and three rectangular faces.
Find the sum of areas of all five faces:
S = 2*(1/2)*16*15 + (17*2 + 16)*12 = 240 + 600 = 840What is the IQR for 10, 14, 15, 15, 16, 18, 19, 21
Answers
Answer:
15-18
Step-by-step explanation:
The IQR is the middle 50% of a set of numbers
There are 8 numbers, so its the middle 4
The middle 4 consists of 15,15,16,18
The range is 15-18
how many red apple are in the jar?
Answers
Answer:
2
Step-by-step explanation:
Which rule explains why these triangles are congruent?
1.SAS
2.ASA
3.SSS
4.AAS
5. These triangles cannot be proven congruent

Answers
Step-by-step explanation:
As we can see from the image,
The triangles ABC and GFH are congruent triangles by the rule ASA theorem as two of their angles and a side length is congruent.
3) Mr. Johnson uses 2.34 yards of yarn to knit a scarf. If Mr. Johnson has a total of 30.42 yards of yarn, how many scarfs will he be able to knit?
Answers
she will be able to knit 13 scarfs
Given ,
Mr. Johnson uses 2.34 yards of yarn to knit a scarfMr. Johnson has a total of 30.42 yards of yarnTo Find : Scarfs Mr John will be able to make if he has 30.42 yards of yarn
2.34 yards of yarn = 1 scarf
30.42 yards of yarn = \(\frac{30.42}{2.34}\)
= 13 scarfs
Hence , the number of scarfs Mr John will make with 30.42 yards of yarn is 13
Find the equation of the line joining the points (2,-8) and (5,6)
Answers
Answer:
y=3/2x-11
x,=2 and x2=5y1= -8 and y2= 6change in y over change in x get x use the formulae\(y = mx + c\)thats the formular u got mfind c using one pair