A rocket is launched in the air. Its height in feet is given by
ℎ
=
−
16
�
2
+
80
�
h=−16t
2
+80t where
�
t represents the time in seconds after launch. Interpret the coordinates of the vertex in context
Answers
(a). The rocket will reach height of 500 feet at 5.12 seconds and 17.38 seconds. (b). The maximum height rocket is 2012.5 feet. (c). The rocket will hit ground at approximately 31.88 seconds.
a) We can substitute h(t) = 500 in given equation and solve for "t".
\(-16t^2 + 400t + 50 = 500\)
\(-16t^2 + 400t - 450 = 0\)
Dividing both sides by -2, we get:
\(8t^2 - 200t + 225 = 0\)
This quadratic equation can be solved using quadratic formula:
\(t = [200 ± sqrt((200)^2 - 4(8)(225))] / (2(8)) \\t = [200 ± sqrt(40000 - 7200)] / 16 \\t = [200 ± sqrt(32800)] / 16 \\\)
t ≈ 5.12 seconds or t ≈ 17.38 seconds
b) The t-coordinate of the vertex can be found using the formula t = -b / 2a:
\(t = -400 / (2(-16)) = 12.5 seconds\)
\(h(12.5) = -16(12.5)^2 + 400(12.5) + 50\) ≈ 2012.5 feet
c) We need to find the value of "t" when h(t) = 0.
\(-16t^2 + 400t + 50 = 0\)
\(-8t^2 + 200t + 25 = 0\)
\(8t^2 - 200t - 25 = 0\)
Using the quadratic formula, we get:
\(t = [200 ± sqrt((200)^2 - 4(8)(-25))] / (2(8))\\t = [200 ± sqrt(40400)] / 16\)
t ≈ 0.62 seconds or t ≈ 31.88 seconds
To know more about vertex, here
brainly.com/question/29030495
#SPJ4
--The complete Question is, A rocket is launched in the air. Its height in feet, "h", is given by the equation h(t) = -16t^2 + 400t + 50, where "t" represents time in seconds after the rocket is launched.
a) At what time(s) will the rocket reach a height of 500 feet?
b) What is the maximum height the rocket will reach?
c) How long will it take for the rocket to hit the ground? --
Related Questions
Please show work and help me please

Answers
Answer:
31.4 in
Step-by-step explanation:
the formula for circumference is 2*\(\pi\)*radius. Since the diameter (which is the radius multiplied by 2) is labeled we can divide 10 by 2 to get the radius. 10/2 is 5. Since pi is an infinite number, we round it to 3.14. Then, plug in the numbers. The expression will be 2*3.14*5. 2* = 10 and 10 * 3.14 you can just move the decimal so the answer is 31.4.
What is the value of tan0 in the unit circle below? (see the attached picture)

Answers
Explanation: To solve this question first we need to know that the terminal point pair (little red point in the image) represented by the coordinates represent the (cosine, sine) as shown bellow
We also need to understand that the "tan" formula can be expressed as follows
\(tan\theta=\frac{sin\theta}{cos\theta}\)So all we need to do is to substitute and calculate.
Step 1: Let's substitute the values and calculate as follows
\(tan\theta=\frac{sin\theta}{cos\theta}=\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}=\frac{1}{2}*\frac{2}{\sqrt{3}}=\frac{2}{2*\sqrt{3}}=\frac{1}{\sqrt{3}}\)Step 2: Now let's rationalize the result as follows
\(tan\theta=\frac{1}{\sqrt{3}}=\frac{1}{\sqrt{3}}*\frac{\sqrt{3}}{\sqrt{3}}=\frac{\sqrt{3}}{3}\)Final answer: So the final answer is
\(\frac{\sqrt{3}}{3}\).

PLEASe heLPPP:((((((

Answers
Answer:
a dollar 1.50
Step-by-step explanation:
you take 4 and multiple by 1.25 which is 5 then you the remaining 3 and divide by 2 which is 1.50
Hope this helps:)
Please help with this question I’m confused on it
PLEASE HELPP

Answers
A. Triangle ABC is similar to triangle DEF.
B. The value of x is 21.
What are similar triangles?
If two triangles have an equal number of corresponding sides and an equal number of corresponding angles, then they are comparable. Similar figures are items that feature more than two figures that are the same shape but different sizes.
Here, we have
Given a triangle and we have to show both triangles are similar.
A. ABC will be similar to DEF if two sides along with their corresponding angle of ABC is equal to two sides and their corresponding angle of DEF. ABC will be similar to DEF if the corresponding ratios of all sides of both triangles are equal to each other.
Hence, triangle ABC is similar to triangle DEF.
B. By the property of similar triangles,
= AB/DE = AC/DF
= 14/x = 10/15
x = 21.
Hence, the value of x is 21.
To learn more about a similar triangle from the given link
https://brainly.com/question/14285697
#SPJ1
y=? what does this even meannnnn

Answers
The calculated measure of angle y is 60 degrees
How to calculate the value of yfrom the question, we have the following parameters that can be used in our computation:
The figure
From the figure, we can see that
The shape can be divided into two triangles such that
Each triangle is an equilateral triangle
The measure of an angle in an equilateral triangle is 60 degrees
using the above as a guide, we have the following:
y = 60
Hence, the value of y is 60 degrees
Read more about angles at
https://brainly.com/question/31898235
#SPJ1
1. What is the circumference of the circle? Use 3.14for 7. Round to the nearest tenth.A. 31.2 ydC. 88.2 ydB. 44.1 ydD. 176.5 yd28.1 yd

Answers
1.-
Circumference = 2 pi r
= 2 * 3.14 * 28.1/2
= 44.1 yd letter B
2.- Circumference = 2*pi* r
= = 2*3.14*11
= 69.08 in letter H
3.- Area = pi*r^2
= 3.14*(9)^2
= 254.34 mm^2 Letter B
PLEASE ANSWER!!!!!!!!!!! SIMPLE MATH PROBLEM PLEASE

Answers
Answer:
False
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightAlgebra I
Equality PropertiesSolving systems of equations using substitution/eliminationStep-by-step explanation:
Step 1: Define Systems
y = 3x - 3
y = -4x + 4
Step 2: Solve for x
Substitution
Substitute in y: 3x - 3 = -4x + 4Isolate x terms: 7x - 3 = 4Isolate x term: 7x = 7Isolate x: x = 1Here we see that our x-value would equal 1.
∴ (-3, 0) is NOT a solution to the systems.
How could you use the function y = sin 2x to find the zeros of y = tan 2x
Answers
To find the zeros of y = tan(2x), we need to solve the equation sin(2x) = 0 to determine the x-values where sin(2x) is zero. These x-values will correspond to the zeros of the function tan(2x).
To find the zeros of the function y = tan(2x), we can utilize the fact that tan(x) is equal to sin(x)/cos(x).
Given y = tan(2x), we can rewrite it as:
y = sin(2x) / cos(2x)
Now, let's consider the numerator of this expression, which is sin(2x). If we set sin(2x) equal to zero, we can determine the values of x that make the numerator zero:
sin(2x) = 0
By solving this equation, we can find the zeros of sin(2x). The solutions will be the values of x for which sin(2x) equals zero.
Similarly, we can look at the denominator of the expression y = sin(2x) / cos(2x), which is cos(2x). If cos(2x) equals zero, the denominator will be zero, which leads to undefined values for y. These points will be vertical asymptotes of the function tan(2x).
To find the zeros of y = tan(2x), we need to solve the equation sin(2x) = 0 to determine the x-values where sin(2x) is zero. These x-values will correspond to the zeros of the function tan(2x).
Learn more about function at https://brainly.com/question/30477134
#SPJ11
For the following triangle,
Answers
Answer:
3 angles?
Step-by-step explanation:
A bag contains 5 yellow, 6 red, and 4 green marbles. Two marbles are drawn. The first is replaced before the second is drawn. A random variable assigns the number of green marbles to each outcome. Calculate the expected value of the random variable. A. 0. 76 c. 0. 27 b. 1. 07 d. 0. 53.
Answers
The expected value of the random variable, representing the number of green marbles drawn, is 0.53 (option d).
To calculate the expected value, we need to multiply each outcome by its corresponding probability and then sum them up. Let's break down the problem:
There are three possible outcomes for the number of green marbles drawn: 0, 1, or 2.
For the outcome of 0 green marbles:
The probability of drawing 0 green marbles can be calculated by selecting both marbles from the non-green marbles in the bag. The probability of drawing a non-green marble on the first draw is (5+6)/(5+6+4) = 11/15. Since the first marble is replaced before the second draw, the probability of drawing a non-green marble on the second draw is also 11/15. Therefore, the probability of getting 0 green marbles is (11/15) * (11/15) = 121/225.
For the outcome of 1 green marble:
The probability of drawing 1 green marble can be calculated by selecting one green marble and one non-green marble. The probability of drawing a green marble on the first draw is 4/15. The probability of drawing a non-green marble on the second draw is 11/15. Since the first marble is replaced, the probability of drawing a non-green marble on the second draw is still 11/15. Therefore, the probability of getting 1 green marble is (4/15) * (11/15) = 44/225.
For the outcome of 2 green marbles:
The probability of drawing 2 green marbles can be calculated by selecting both marbles from the green marbles in the bag. The probability of drawing a green marble on the first draw is 4/15. Since the first marble is replaced, the probability of drawing a green marble on the second draw is also 4/15. Therefore, the probability of getting 2 green marbles is (4/15) * (4/15) = 16/225.
Now, we can calculate the expected value by multiplying each outcome by its probability and summing them up:
Expected Value = (0 * (121/225)) + (1 * (44/225)) + (2 * (16/225))
= 0 + (44/225) + (32/225)
= 76/225
≈ 0.337
Rounded to two decimal places, the expected value of the random variable, representing the number of green marbles drawn, is approximately 0.34 (option d).
Learn more about random variable here
https://brainly.com/question/17217746
#SPJ11
A booth in a mall sells calendars. The calendars are purchased for $3.26 each and then sold to customers at a price of $11.21. Space is rented for $185.00 per day and wages amount to $271.00 per day. Answer each of the following independent questions. (a) If the wages decrease to $219.51 per day, and other variables remain the same, how many calendars must be sold to break even? (b) If the calendars are put on sale at 20% off the regularprice, and all other variables remain the same, calculate profits if 206 calendars are sold in a day?
Answers
(a) To break even, the number of calendars that must be sold is 102. (b) The profit from selling 206 calendars at a 20% discount is $746.22.
(a) To calculate the number of calendars that must be sold to break even, we need to consider the total costs and the selling price per calendar. The total costs consist of the sum of space rental and wages per day, which is $185.00 + $271.00 = $456.00.
The profit per calendar is the selling price minus the purchase price, which is $11.21 - $3.26 = $7.95. To break even, the total profit should cover the total costs, so we divide the total costs by the profit per calendar: $456.00 / $7.95 = 57.48. Since we cannot sell a fraction of a calendar, we round up to the nearest whole number, which is 58. Therefore, 58 calendars must be sold to break even.
(b) To calculate the profit from selling 206 calendars at a 20% discount, we first need to determine the discounted selling price. The discount is 20% of the regular selling price, which is 0.20 * $11.21 = $2.24. The discounted selling price is then $11.21 - $2.24 = $8.97 per calendar.
The profit per calendar is the discounted selling price minus the purchase price, which is $8.97 - $3.26 = $5.71. Multiplying the profit per calendar by the number of calendars sold gives us the total profit: $5.71 * 206 = $1,176.26. Therefore, the profit from selling 206 calendars at a 20% discount is $1,176.26.
Learn more about profit here:
https://brainly.com/question/29055465
#SPJ11
A) Determine whether the sequence converges or diverges. If it converges, find the limit. (If an answer does not exist, enter DNE.)an = ln(3n4 + 4) − ln(7n2 + 2)lim n→[infinity] an = ?
Answers
The sequence an = ln(3n^2 + 4) − ln(n^2 + 4) converges to ln(3) as n approaches infinity.
To find the limit of the sequence an = ln(3n^2 + 4) − ln(n^2 + 4) as n approaches infinity, we can use algebraic manipulation and properties of limits
an = ln(3n^2 + 4) − ln(n^2 + 4)
= ln[(3n^2 + 4)/(n^2 + 4)]
= ln[3 + 4/n^2]/[1 + 4/n^2]
= ln(3) + ln[1 + (4/n^2)] − ln[1 + (4/n^2)]
= ln(3)
As n approaches infinity, the expression inside the natural logarithm approaches 3, so the limit of the sequence is ln(3):
\(\lim_{n \to \infty} a_n\) = ln(3)
Therefore, the sequence converges to ln(3).
Learn more about convergence here
brainly.com/question/21961097
#SPJ4
The given question is incomplete, the complete question is:
A) Determine whether the sequence converges or diverges. If it converges, find the limit. (If an answer does not exist, enter DNE.)
an = ln(3n^2 + 4) − ln(n^2 + 4)
lim n→∞ an = ?
A single tractor-trailer driver is starting a new shift, intending to travel 450 miles from Charlotte, NC to Pittsburgh, PA. Estimating an average speed of 50 mph and abiding by the current HOS rules, what is the minimum number of clock hours (not driving hours) it will take him?
Answers
It will take a minimum of 10 clock hours (not driving hours) for the truck driver to travel 450 miles from Charlotte, NC to Pittsburgh, PA.
The current Hours of Service (HOS) rules for truck drivers stipulate that a truck driver cannot drive for more than 11 hours after 10 consecutive hours off duty.
Additionally, the driver is not allowed to drive beyond 14 hours after coming on duty.
The driver's shift includes both driving and non-driving time.
Therefore, it is necessary to consider the total amount of time spent on the job.
The truck driver will have to stop for rest breaks, refueling, or other reasons during the 450-mile journey to Pittsburgh, Pennsylvania. The driver is required to take a 30-minute break after eight hours of driving.
Therefore, the minimum number of clock hours (not driving hours) it will take the truck driver to travel the 450-mile distance from Charlotte, NC to Pittsburgh, PA is calculated as follows:
Time for the trip = (Distance ÷ Average Speed) + Breaks
Time for the trip = (450 ÷ 50) + (30 ÷ 60) × 2
Time for the trip = 9 + 1
Time for the trip = 10 clock hours
Therefore, it will take a minimum of 10 clock hours (not driving hours) for the truck driver to travel 450 miles from Charlotte, NC to Pittsburgh, PA.
Know more about Hours of Service (HOS) here:
https://brainly.com/question/32726922
#SPJ11
Consider the following definite integral.sxex²+1d'dx0Identify the definite integral that will result after making a u-substitution.
Answers
The first choice is the correct result
Heather purchased a new $1,500 laptop by using a credit card with a 17% interest rate. She will pay off the balance in 2 years by paying monthly payments of $74.16. Calculate Heather’s total cost of repayment.
Answers
12 months in a year
2 years
2x12=24
74.16x24=1779.84
Heather's total cost of repayment is $1,779.84.
What exactly is a monthly payment?A monthly payment is a payment made every month to pay off loans or advances. It's similar to EMI.
Given,
Principal = $1,500
Rate = 17% per year (or 0.17 as a decimal)
Time = 2 years
Total interest = (principal × rate × time) / 12
Substitute the given values, and we get:
Total interest = (1500 × 0.17 × 2) / 12 = $51
So, Heather will pay a total of $51 in interest over the two years.
Total repayment = monthly payment × number of months
Here,
Monthly payment = $74.16
Number of months = 2 years × 12 months/year = 24 months
Substitute these values, and we get:
Total repayment = $74.16 × 24 = $1,779.84
Therefore, Heather's total cost of repayment is $1,779.84.
Learn more about the monthly payments here:
https://brainly.com/question/20761642
#SPJ3
Questions 18-30 pls help due tomorrow

Answers
Answer:
Step-by-step explanation:
30
Step-by-step explanation:
以下の情報を添えて、このチラシを当社の登録従業員の 1 人に渡してください。 より多くのチラシを提出した先生がピザ パーティーを勝ち取ります。
Describe the graph y=|x-2|+4
A) a V shaped graph with vertex at(-2,4) which opens up.
B) a V shaped graph with vertex at (4,-2) which opens down
C)a V shaped graph with vertex at(4,2) which opens down
D) a V shaped graph with vertex at(2,4) which opens up
Answers
Answer: D) a V shaped graph with vertex at(2,4) which opens up
Step-by-step explanation:
Answer:
d
any more help just ask :)
A 2000 lb ration contains 1600 lbs of corn and 400 lbs of distillers grains. Corn is 9% protein and distillers grains is 27% protein. How many lbs of protein are contained in a ton of feed
Answers
There are 360 lbs of protein in a ton of feed. Given:Weight of ration = 2000 lbsWeight of corn = 1600 lbsWeight of distillers grain = 400 lbsThe percentage of protein in corn = 9%The percentage of protein in distillers grains = 27%Now, to find out how many pounds of protein are contained in a ton of feed,
we first need to convert the weight of the feed to tons:1 ton = 2000 lbsSo, the weight of the feed in tons = 2000/2000 = 1 tonNow, we need to find out how much protein is contained in 1 lb of corn and distillers grains respectively:In 1 lb of corn, the protein content is 9%.So, the protein content in 1600 lbs of corn = 9% of 1600= 0.09 x 1600= 144 lbsIn 1 lb of distillers grains, the protein content is 27%.So, the protein content in 400 lbs of distillers grains = 27% of 400= 0.27 x 400= 108 lbsTherefore, the total weight of protein in 1 ton of feed = 144 + 108= 252 lbsBut we need the weight of protein in a ton, which is 2000 lbs.
So, we can set up a proportion as follows:1 ton of feed contains 252 lbs of proteinTherefore, x tons of feed contain 2000 lbs of protein.So, x = (2000/252) x 1 = 7.936507936507937 (rounded to 3 decimal places)Therefore, the answer is that there are 360 lbs of protein in a ton of feed.
To know more about percentage visit:
https://brainly.com/question/16797504
#SPJ11
help pleasejhdfjg THIS ASSIGNMENT IS LIKE 2 WEEKS OVERDUE

Answers
a) A 2*2 area model would not work to multiply (x + 3)(2x⁴ − 3x³ − 2x² − 4x − 1) because this expression has 5 terms, and a 2*2 area model can only accommodate 4 smaller areas (b) The area model for (x + 3)(2x⁴ − 3x³ − 2x² − 4x − 1) with the correct lengths and widths labeled has been attached below. (c) The final total area is 2x² - 10x - 15.
What is an area model?An area model is a way to visualize multiplication by breaking up the larger rectangle into smaller rectangles whose areas represent the products of the terms being multiplied. To determine the correct rows and columns for the area model, we count the number of terms in each factor and use that as a guide. For example, if one factor has 3 terms and the other has 4 terms, we would use a 3x⁴ area model, with 3 rows and 4 columns.
a) A 2*2 area model would not work to multiply (x + 3)(2x⁴ − 3x³ − 2x² − 4x − 1) because this expression has 5 terms, and a 2*2 area model can only accommodate 4 smaller areas.
b) The area model for (x + 3)(2x⁴ − 3x³ − 2x² − 4x − 1) with the correct lengths and widths labeled has been attached below.
2x⁴ − 3x³ − 2x² − 4x − 1
+---------------------------------------
x | 2x⁵ -3x⁴ -2x³ -4x² -x
|
3 | 6x⁴ -9x³ -6x² -12x -3
+---------------------------------------
c) To find the total area of a rectangle with length (x + 8) and width (x − 5), we can use an area model with 2 rows and 2 columns. The length (x + 8) corresponds to one dimension of the rectangle, while the width (x − 5) corresponds to the other dimension. The area of each smaller rectangle in the model represents the product of one term from each factor.
x + 8 x - 5
+--------------------
x | x² + 8x x² - 5x
|
-5 | -5x + -40 -5x + 25
+--------------------
The final total area can be found by adding up the areas of the smaller rectangles:
Total area = x² + 8x + x² - 5x - 5x - 40 + 25
= 2x² - 10x - 15
= 2x² - 10x - 15.
Read more about area model on https://brainly.com/question/30729476
#SPJ1
Write two equivalent expressions that represent the rectangular array below.

Answers
Answer: 3 x 2a + 3 x 5 = 3 x 2a x 5
You know that the expressions are equivalent, because when you solve for a you get a = 5/8 or 0.625
The rectangular array is represented by the equations "3*(5 + 2a)" and "3*2a*5 + 3*5".
What is expression?Any mathematical statement that includes numbers, variables, and an arithmetic operation between them is known as an expression or an algebraic expression.
given, two rectangles whose one side is equal that is 3.
expression for the area of the rectangle for the first rectangle = 3 * 2a
expression for the area of the rectangle for the second rectangle =
3*(5 + 2a)
Since Expressions are equivalent
3*2a*5 + 3*5 = 3*(5 + 2a)
therefore, two equivalent expressions representing the rectangular array are "3*(5 + 2a)" and "3*2a*5 + 3*5".
Learn more about expression here:
https://brainly.com/question/24242989
#SPJ2
What happens to the value of the expression 80-2r80−2r80, minus, 2, r as rrr decreases? Choose 1 answer: Choose 1 answer: (Choice A) A It increases. (Choice B) B It decreases. (Choice C) C It stays the same. Stuck?Watch a video or use a hint.
Answers
Answer:
(Choice B) B It decreases.
Step-by-step explanation:
According to the situation, the solution of the value of the expression is as follows
Let us assume
r 80 -2r
5 80 - 10 = 70
4 80 - 8 = 72
3 80 - 6 = 74
2 80 - 4 = 76
1 80 - 2 = 78
As we can from the above calculation that expression value risen if r value decreased
Therefore the correct option is B.
Answer:
It increases
Step-by-step explanation:
1a.)Given a force =15 N, cctry at an angle 45
∘
N⋅w. What are its components? b.) Given the comporents at a force one (5,5) Newton. What is the valve force:N and its direction (θ:?) 1c.) Two children are pulling a cart. Child (A) is walking East and at 5 m/s. Child (B) is walking North at 7mls. What is the resoltont velocity and its directon? 1d.) Given the following comporents of V
A
(5,1),V
B
(7,7), unat is the values of the resultant and Its direction?
Answers
The components of the force are approximately Fx = 10.61 N and Fy = 10.61 N. The magnitude of the force is approximately 7.07 N, and its direction is approximately 45 degrees.
a) To find the components of a force at an angle of 45 degrees with a magnitude of 15 N, we can use trigonometry.
Let's assume the force has components Fx and Fy.
Fx = F * cos(θ) = 15 N * cos(45°) = 15 N * (√2/2) ≈ 10.61 N
Fy = F * sin(θ) = 15 N * sin(45°) = 15 N * (√2/2) ≈ 10.61 N
So, the components of the force are approximately Fx = 10.61 N and Fy = 10.61 N.
b) Given the components of a force as (5, 5) Newton, we can use the Pythagorean theorem and trigonometry to find the magnitude and direction.
Magnitude of the force:
|F| = √(Fx² + Fy²) = √(5² + 5²) = √50 ≈ 7.07 N
Direction of the force:
θ = tan⁻¹(Fy / Fx) = tan⁻¹(5 / 5) = tan⁻¹(1) ≈ 45°
So, the magnitude of the force is approximately 7.07 N, and its direction is approximately 45 degrees.
c) To find the resultant velocity of two children pulling a cart, we can use vector addition.
Let's assume the velocity of child A is Va = 5 m/s (east) and the velocity of child B is Vb = 7 m/s (north).
The resultant velocity (Vr) can be found by adding the vectors Va and Vb:
Vr = Va + Vb = 5 m/s (east) + 7 m/s (north)
To find the magnitude and direction of Vr, we can use the Pythagorean theorem and trigonometry:
Magnitude of Vr:
|Vr| = √(Vx² + Vy²) = √((5 m/s)² + (7 m/s)²) ≈ √74 ≈ 8.60 m/s
Direction of Vr:
θ = tan⁻¹(Vy / Vx) = tan⁻¹((7 m/s) / (5 m/s)) ≈ 54.47°
So, the resultant velocity is approximately 8.60 m/s at an angle of 54.47 degrees north of east.
d) Given the components of VA as (5, 1) and VB as (7, 7), we can find the resultant vector VR by adding VA and VB.
VR = VA + VB = (5 + 7, 1 + 7) = (12, 8)
To find the magnitude and direction of VR, we can use the Pythagorean theorem and trigonometry:
Magnitude of VR:
|VR| = √(Vx² + Vy²) = √((12)² + (8)²) = √(144 + 64) = √208 ≈ 14.42
Direction of VR:
θ = tan⁻¹(Vy / Vx) = tan⁻¹(8 / 12) ≈ 33.69°
So, the magnitude of the resultant vector is approximately 14.42, and its direction is approximately 33.69 degrees.
Learn more about Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ11
If P(B)=
4
1
,P(A∪B)=
2
1
and P(A∣B)=
3
2
, then which of the following statements is true? A) P(A)=
3
1
B) P(A∩B)=
12
1
C) P(B∣A)=
5
1
D) A and B are not independent.
Answers
None of the statements A, B, or C can be determined to be true based on the given information. we do not have enough information to determine the values of P(A), P(A∩B), or P(B|A) from the given probabilities.
To determine which statement is true, let's analyze the given information. We have:
P(B) = 4/1
P(A∪B) = 2/1
P(A|B) = 3/2
Let's evaluate each statement:
A) P(A) = 3/1
This statement is not directly supported by the given information. We cannot determine the value of P(A) solely based on the provided probabilities.
B) P(A∩B) = 12/1
This statement is also not supported by the given information. We do not have enough information to determine the value of P(A∩B).
C) P(B|A) = 5/1
This statement is not supported by the given information. We do not have any direct information about P(B|A), so we cannot determine its value.
D) A and B are not independent.
To determine whether A and B are independent, we can check if P(A∩B) = P(A) * P(B). However, as mentioned earlier, we do not have enough information to determine the value of P(A∩B). Therefore, we cannot conclude whether A and B are independent based on the given information.
In summary, none of the statements A, B, or C can be determined to be true based on the given information. The only conclusion we can draw is that we do not have enough information to determine the values of P(A), P(A∩B), or P(B|A) from the given probabilities.
Learn more about probabilities.
https://brainly.com/question/29381779
#SPJ11
Please help. Calculus level math problem on anti-derivatives, I don't need an explanation just an answer.

Answers
All times in the interval 0 ≤ t ≤ π/2 are π/8, π/6, π/4 respectively.
What is the general form of velocity?
The general form of a velocity function is \(v(t) = v_0 + at\)
where,
v(t) is the velocity of an object at time t, \(v_0\) is the initial velocity of the object, a is the acceleration of the object
This formula assumes constant acceleration. If the acceleration is not constant, then the formula becomes more complex, involving calculus and integration.
We can start by integrating the acceleration function to get the velocity function:
v(t) = ∫ a(t) dt = ∫ 8 cos (4t) dt = 2 sin (4t) + C
We know that v(π/8) = 1, so we can use this information to solve for the constant C:
1 = 2 sin (4π/8) + C
1 = 2 sin (π/2) + C
1 = 2 + C
C = -1
Therefore, the velocity function is v(t) = 2 sin (4t) - 1
To determine when the particle is moving to the right, we need to find when its velocity is positive. We can write:
v(t) > 0
2 sin (4t) - 1 > 0
sin (4t) > 1/2
4t > π/6 or 4t < 5π/6
t > π/24 or t < 5π/24
Since we are only interested in the interval 0 ≤ t ≤ π/2, we need to check which of these solutions fall within this interval:
π/24 < π/8 and 5π/24 > π/8
So the particle is moving to the right at times t = π/8, t = π/6, and t = π/4, which are the solutions that fall within the given interval.
Learn more about time here,
https://brainly.com/question/1047465
#SPJ1
Frankie dad made scrambled egg for the family breakfast he started with full carton of 12 egg he used 8of the Egg what the fraction of the carton of egg did he use write at least two equivalent fraction
Answers
solve for x in this equation below
9+3x=10
Answers
Answer:
in fraction form it is X= 1/3
in decimal form it is X= 0.3 rep.
Step-by-step explanation:
What are the possible values of ml for each of the following values of l?
A) 0 Express your answers as an integer. Enter your answers in ascending order separated by commas.
B) 1 Express your answers as an integer. Enter your answers in ascending order separated by commas.
C) 2 Express your answers as an integer. Enter your answers in ascending order separated by commas.
D) 3 Express your answers as an integer. Enter your answers in ascending order separated by commas.
Answers
The possible values of ml for each value of l are as follows:
- For l = 0, ml = 0
- For l = 1, ml = -1, 0, 1
- For l = 2, ml = -2, -1, 0, 1, 2
- For l = 3, ml = -3, -2, -1, 0, 1, 2, 3.
The values of ml represent the orientation of the orbital in a given subshell. The possible values of ml depend on the value of l, which is the angular momentum quantum number. The values of l determine the shape of the orbital.
For l = 0, which corresponds to the s subshell, there is only one possible value of ml, which is 0. This indicates that the s orbital is spherical in shape and has no orientation in space.
For l = 1, which corresponds to the p subshell, there are three possible values of ml, which are -1, 0, and 1. This indicates that the p orbital has three orientations in space, corresponding to the x, y, and z axes.
For l = 2, which corresponds to the d subshell, there are five possible values of ml, which are -2, -1, 0, 1, and 2. This indicates that the d orbital has five orientations in space, corresponding to the five axes that can be derived from the x, y, and z axes.
For l = 3, which corresponds to the f subshell, there are seven possible values of ml, which are -3, -2, -1, 0, 1, 2, and 3. This indicates that the f orbital has seven orientations in space, corresponding to the seven axes that can be derived from the x, y, and z axes.
It is important to note that the values of ml are always integers, and they range from -l to +l. The ml values describe the orientation of the orbital in space and play an important role in understanding the electronic structure of atoms and molecules.
To know more about orientation of the orbital visit:
https://brainly.com/question/12497259
#SPJ11
1. On a standardized test, Cathy had a score of 74, which was exactly 1 standard deviation
below the mean. If the standard deviation for the test is 6, what is the mean score for
the test?
Answers
The mean score for the test is 80.
We have,
To find the mean score for the test, we can use the relationship between the mean, the standard deviation, and the z-score.
The formula for the z-score is:
z = (x - μ) / σ
Where:
z is the z-score,
x is the given score,
μ is the mean, and
σ is the standard deviation.
In this case, we know that Cathy's score (x) is 74 and it is 1 standard deviation below the mean (z = -1).
The standard deviation (σ) is given as 6.
Plugging these values into the z-score formula, we can solve for the mean (μ):
-1 = (74 - μ) / 6
Multiplying both sides by 6:
-6 = 74 - μ
Rearranging the equation:
μ = 74 + 6
μ = 80
Thus,
The mean score for the test is 80.
Learn more about mean here:
https://brainly.com/question/23263573
#SPJ12
Please I keep getting stuck on this I need help so bad!
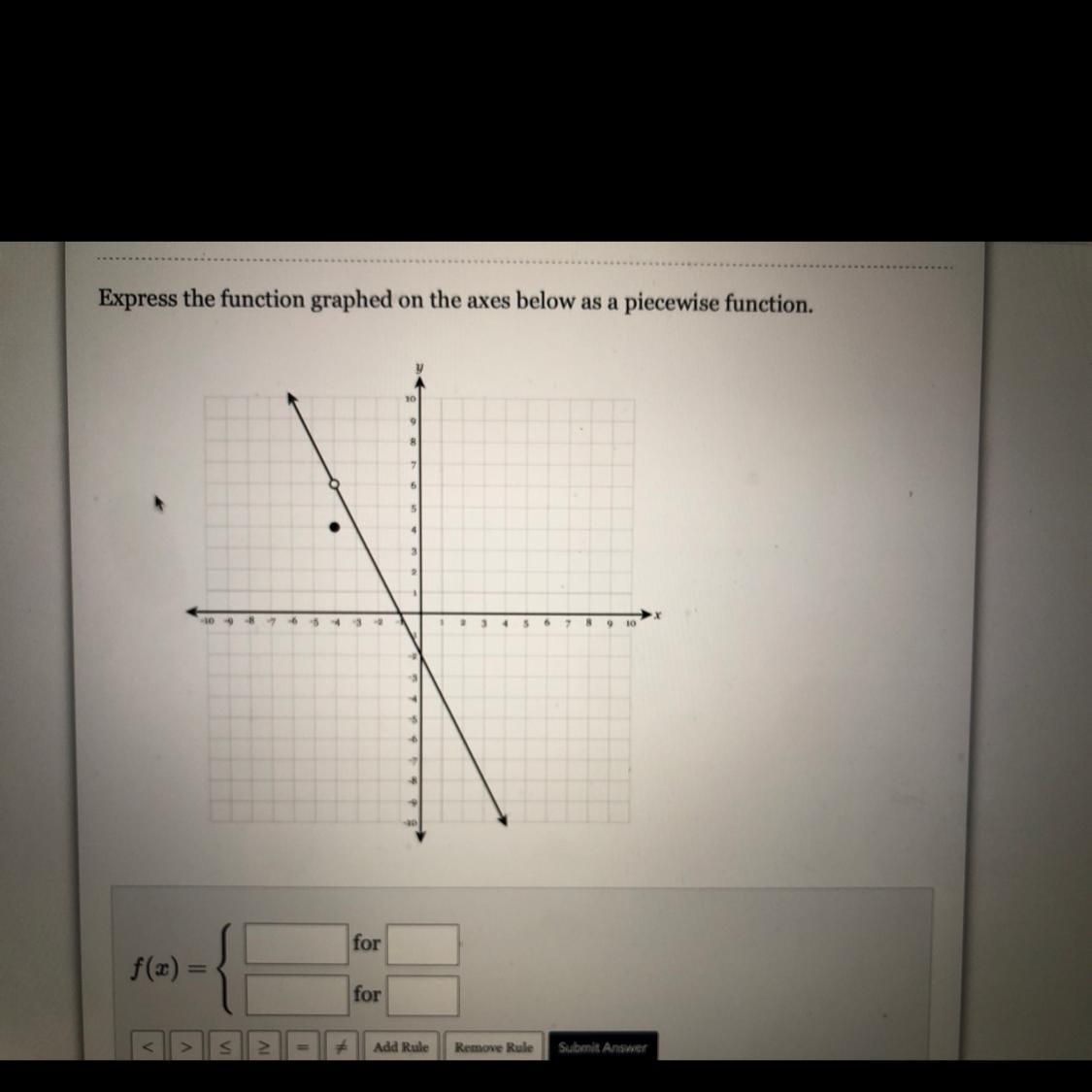
Answers
Answer:
f(x) = -2x -2 ; -∞ < x < -4 and -4 < x < ∞
6 ; x = -4
Step-by-step explanation:
Piecewise function:(-1,0) and (0 ,-2)
Find the slope using the points.
\(\sf slope =\dfrac{y_2-y_1}{x_2-x_1}\)
\(\sf = \dfrac{-2-0}{0-(-1)}\\\\=\dfrac{-2}{0+1}\\\\=-2\)
m = -2
Equation of line in slope y-intercept form: y =mx + b
y = -2x + b
Plugin any of the point in the above equation. (0, -2)
-2 = 0 + b
b = -2
Equation: y = -2x - 2
Hollow circle is the break point.
Function:
f(x) = -2x -2 ; -∞ < x < -4 and -4 < x < ∞
6 ; x = -4
The function graphed on the axes below as a piecewise function is \($f(x)=\left\{\begin{array}{l}-x-1, \text { for }-6 \leq x < 2 \\ -\frac{1}{2} x-4, \text { for } 2 < x < 6\end{array}\right.$\)
The upper piece of the graph is defined on the interval \($-6 \leq x < 2$\). It has a slope of -1 and a y-intercept of -1, so its equation is \($y=-x-1$\).
The lower piece of the graph is defined on the interval \($2 < x < 6$\). It has a slope of -1 / 2 and would cross the y-axis at -4 if it were extended. Its equation is
\(y=-1 / 2 x-4\)
The two pieces together give the function.
\(f(x)=\left\{\begin{aligned}-x-1, & \text { for }-6 \leq x < 2 \\-\frac{1}{2} x-4, \text { for } 2 < x < 6\end{aligned}\right.$$\)
The core concept of mathematics' calculus is functions. The unique varieties of relations are the functions. In mathematics, a function is represented as a rule that produces a distinct result for each input x. In mathematics, a function is indicated by a mapping or transformation. Typically, these functions are identified by letters like f, g, and h. The collection of all the values that the function may input while it is defined is known as the domain. The entire set of values that the function's output can produce is referred to as the range. The set of values that could be a function's outputs is known as the co-domain.
To learn more function visit:
brainly. com/question/12431044
#SPJ1
potassium 42 has a decay rate of 5.5% per hour. in how many hours will the original quantity be halved?
Answers
The half-life of Potassium-42 can be calculated using the following formula:
t1/2 = (ln 2) / λ
where t1/2 is the half-life, ln is the natural logarithm, and λ is the decay rate.
Substituting the values given, we get:
t1/2 = (ln 2) / 0.055
t1/2 ≈ 12.6 hours
Therefore, the original quantity of Potassium-42 will be halved in approximately 12.6 hours.
It will take approximately 13.51 hours for the original quantity of potassium 42 to be halved with a decay rate of 5.5% per hour.
How we can understand about how many hours will the original quantity be halved?To find the number of hours it takes for potassium 42 to be halved with a decay rate of 5.5% per hour, we can use the formula:
Since we want the final quantity to be half of the original quantity, we can set up the equation:
0.5 * Original quantity = Original quantity * (1 - 0.055) ^ time
Now, we can solve for time:
0.5 = (1 - 0.055) ^ time
log(0.5) = time * log(0.945)
time = log(0.5) / log(0.945)
Calculating the value, we get:
time ≈ 13.51 hours
Learn more about Original Quantity
brainly.com/question/29336831
#SPJ11