a researcher had participants eat the same flavored ice cream packaged in a round or square carton. the participants then indicated how much they liked the ice cream. the dependent variable is:
Answers
The amount they liked the ice cream is what is being measured in this experiment. Thus, it is the dependent variable.
The dependent variable in this experiment is how much the participants liked the ice cream.
A dependent variable is a variable that is being observed or measured for changes in the experiment.
It is the effect or outcome that the experimenter wants to investigate or explain.
In contrast, an independent variable is a variable that is manipulated or changed by the experimenter in order to observe the effect on the dependent variable.
In the given experiment, the participants ate the same flavored ice cream packaged in either a round or square carton.
Then, they indicated how much they liked the ice cream.
The amount they liked the ice cream is what is being measured in this experiment.
Thus, it is the dependent variable.
Know more about dependent variable here:
https://brainly.com/question/25223322
#SPJ11
Related Questions
when a fair die is tossed twice, what is the probability that the same number appears twice (round off to second decimal place)?
Answers
The probability that the same number appears twice is 0.16
What is probability?
Simply put, probability measures how probable something is to occur. We can discuss the probabilities of various outcomes, or how likely they are, whenever we are unsure of how an event will turn out. Statistics is the study of events subject to probability.
The fair die is thrown twice.
The total number of outcomes if a fair die is tossed twice is 36.
The favorable number of outcomes, which also contains six, is six.
Following is a calculation of the likelihood of the same number appearing twice.
Probability = (Number of possible outcomes)/(Total number of outcomes)
= 6/36
= 0.16
So, the probability is 0.16
To learn more about the probability from the given link
https://brainly.com/question/24756209
#SPJ4
A scuba diver Dives to -13. 75 Ft on Monday on Tuesday she died four times as deep as Monday how deep does the scuba diver dive on a Tuesday write a rational number to represent the diverse location to relevant to the surface of the water
Answers
Therefore, the diver's depth from the surface on Monday can be expressed as -13.75/1 and it is a rational number.
On Monday, divers dive to a depth of -13.75 feet.
On Tuesday he dives four times as deep as he did on Monday. So here's how deep she dives on Tuesday.
4 x (-13.75) = -55 feet
To precise a diver's profundity as a rational number, we have to express it as a division where the numerator is the profundity over the surface and the denominator is the unit of degree (feet in this case).
Therefore, the diver's depth from the surface on Monday can be expressed as -13.75/1.
On Tuesday, the diver's depth from the surface can be expressed as -55/1. So on Tuesday, divers dive to a depth of -55 feet, which can be expressed as the rational number -55/1.
learn more about rational numbers
brainly.com/question/24398433
#SPJ4
Simplify this expression.
–6w + (–8.3) + 1.5+ (–7w)
Answers
The simplified form of the expression -6w + (–8.3) + 1.5+ (–7w) is -13w - 6.8.
What is the simplified form of the expression?Given the expression in the question;
-6w + (–8.3) + 1.5+ (–7w)
To simplify, first remove the parenthesis
Note that;
- × + = -- × - = ++ × + = +-6w + × - 8.3 + 1.5 + × - 7w
-6w - 8.3 + 1.5 - 7w
Next collect and add like terms
-6w - 7w - 8.3 + 1.5
Add -6w and -7w
-13w - 8.3 + 1.5
Add -8.3 and 1.5
-13w - 6.8
Therefore, -13w - 6.8 is the simplified form.
Learn more about expressions here: https://brainly.com/question/28959918
#SPJ1
find the exact length of the curve y=x36+12x,12≤x≤1.
Answers
Now, we can set up the integral to calculate the length of the curve:
\(L = ∫[a, b] √(1 + (dy/dx)^2) dx\)
\(L = ∫[12, 1] √(1 + (3x^2 + 12)^2) dx\)
What is Arhac length.?
Arc length refers to the length of a curve in a two-dimensional space. It represents the distance along the curve between two points. Arc length is calculated using mathematical methods, such as integration, to measure the length of a curve segment. It is an important concept in calculus and geometry, with applications in various fields, including physics, engineering, and computer graphics.
To find the exact length of the curve\(y = x^3 + 12x\), over the interval 12 ≤ x ≤ 1, we can use the arc length formula for a curve in Cartesian coordinates.
The arc length formula is given by:
\(L = ∫[a, b] √(1 + (dy/dx)^2) dx\)
First, let's find dy/dx for the given function\(y = x^3 + 12x:\)
\(dy/dx = 3x^2 + 12\)
Next, let's square and simplify the expression inside the square root:
\((1 + (dy/dx)^2) = 1 + (3x^2 + 12)^2\)
Now, we can set up the integral to calculate the length of the curve:
\(L = ∫[a, b] √(1 + (dy/dx)^2) dx\)
\(L = ∫[12, 1] √(1 + (3x^2 + 12)^2) dx\)
Unfortunately, this integral does not have a simple closed-form solution. Therefore, to find the exact length of the curve, numerical methods or approximations would need to be employed.
To know more about Arc length. visit:
https://brainly.com/question/30582409
#SPJ4
write each of the following polynomials as a product of irreducible polynomials over the given field. (a) 2x3 x2 2 over f3 (d) x4 x3 2x2 x 2 over f3
Answers
A quartic polynomials is more complicated than quadratic or cubic polynomials. There are no obvious linear or quadratic factors. It is possible that the polynomial x^4 + x^3 + 2x^2 + x + 2 is irreducible over F3.
The polynomial 2x³ + 2x² + 2 over the field F₃, we first notice that we can factor out a 2 from all three terms to obtain:
2(x³ + x² + 1)
Now we need to factor the polynomial x³ + x² + 1 over F₃. One way to do this is to simply plug in all possible values for x (which are 0, 1, and 2 in F₃) and see if any of them result in a zero polynomial. We find that none of them do, so we know that x³ + x² + 1 is irreducible over F₃.
Therefore, our final factorization of 2x³ + 2x² + 2 over F₃ is:
2(x³ + x² + 1)
(b) To factor the polynomial x⁴ + x³ + 2x² + x + 2 over F₃, we can start by plugging in all possible values for x and checking if any of them result in a zero polynomial. Doing so, we find that x = 1 is a root of the polynomial, which means that x - 1 is a factor. Using polynomial long division or synthetic division, we can divide x⁴ + x³ + 2x² + x + 2 by x - 1 to obtain:
x⁴ + x³ + 2x² + x + 2 = (x - 1)(x³ + 2x² + 4x + 2)
Now we need to factor the cubic polynomial x³ + 2x² + 4x + 2 over F₃. Again, we can plug in all possible values for x and check for roots, but we won't find any in this case. However, we can use the fact that the sum of the coefficients of the polynomial is zero (1 + 2 + 4 + 2 = 0 in F₃) to infer that x = 1 is a root mod 3, and therefore x - 1 is a factor. Dividing x³ + 2x² + 4x + 2 by x - 1 using polynomial long division or synthetic division, we obtain:
x³ + 2x² + 4x + 2 = (x - 1)(x² + 3x + 2)
Now we need to factor the quadratic polynomial x² + 3x + 2 over F₃. We can do this by factoring it as (x + 1)(x + 2), since (x + 1)(x + 2) = x² + 3x + 2 mod 3.
Therefore, our final factorization of x⁴ + x³ + 2x² + x + 2 over F₃ is:
(x - 1)(x + 1)(x + 2)²
To know more about polynomials here
https://brainly.com/question/25566088
#SPJ4
Cho hàm Bool 4 biến x, y, z, t với: f -1 (1) = {1010, 1110, 0110, 0010, 1011, 0111, 0011, 1001, 1101, 0001, 1000, 1100, 0100, 0000
Answers
!!! PLEASE HELP !!! Clare made green paint with 4 cups of yellow paint and 5 cups of blue paint. If Ms.
Kim only has 1 cup of blue paint, how much yellow paint should she use to get the
same color green?
Answers
Answer:
1/2 cup blue
blahnik black gg fu lrjrhjrjrek
Answer:
bshdjrjrb
Step-by-step explanation:
abcdefghijklmnop
what are the major methods of recording unstructured observational data
Answers
The major methods of recording unstructured observational data are Narrative Description, Field Notes, Audio or Video Recording, Photography, Diagrams or Maps.
The major methods of recording unstructured observational data are:
1. Narrative Description: This method involves writing a detailed, chronological account of the observed events or behaviors, capturing the context and interactions as they occur naturally.
2. Field Notes: In this method, the observer takes brief, concise notes during the observation, focusing on key events, behaviors, or interactions. These notes can be expanded and organized later for further analysis.
3. Audio or Video Recording: Using audio or video equipment, the observer captures the events and interactions in their entirety. This allows for a more accurate record and the ability to review and analyze the data multiple times.
4. Photography: Taking photographs during the observation can provide a visual record of the events and behaviors. These images can supplement other data collection methods and help to illustrate specific aspects of the observation.
5. Diagrams or Maps: Drawing diagrams or maps of the observation setting can help capture the spatial relationships between individuals and objects, as well as the overall layout of the environment.
These methods can be used individually or in combination, depending on the research question and the specific needs of the study. Remember to always respect participants' privacy and obtain informed consent when necessary.
To learn more about unstructured data
https://brainly.com/question/30977617
#SPJ11
Hola me pueden ayudar con matematica

Answers
Tienes la tarea en Ingles? Yo solo puedo hacer mathematics en ingles. Gracias.
$n$ is a four-digit positive integer. dividing $n$ by $9$, the remainder is $5$. dividing $n$ by $7$, the remainder is $3$. dividing $n$ by $5$, the remainder is $1$. what is the smallest possible value of $n$?
Answers
To find the smallest possible value of $n$, we need to find the smallest value that satisfies all three conditions.
From the first condition, we know that $n = 9a + 5$ for some positive integer $a$.
From the second condition, we know that $n = 7b + 3$ for some positive integer $b$.
From the third condition, we know that $n = 5c + 1$ for some positive integer $c$.
We can set these equations equal to each other and solve for $n$:
$9a + 5 = 7b + 3 = 5c + 1$
Starting with the first two expressions:
$9a + 5 = 7b + 3 \Rightarrow 9a + 2 = 7b$
The smallest values of $a$ and $b$ that satisfy this equation are $a=2$ and $b=3$, which gives us $n = 9(2) + 5 = 7(3) + 3 = 23$.
Now we need to check if this value of $n$ satisfies the third condition:
$n = 23 \not= 5c + 1$ for any positive integer $c$.
So we need to try the next possible value of $a$ and $b$:
$9a + 5 = 5c + 1 \Righteous 9a = 5c - 4$
$7b + 3 = 5c + 1 \Righteous 7b = 5c - 2$
If we add 9 times the second equation to 7 times the first equation, we get:
$63b + 27 + 49a + 35 = 63b + 45c - 36 + 35b - 14$
Simplifying:
$49a + 98b = 45c - 23$
$7a + 14b = 5c - 3$
$7(a + 2b) = 5(c - 1)$
So the smallest possible value of $c$ is 2, which gives us $a + 2b = 2$. The smallest values of $a$ and $b$ that satisfy this equation are $a=1$ and $b=1$, which gives us $n = 9(1) + 5 = 7(1) + 3 = 5(2) + 1 = 46$.
Therefore, the smallest possible value of $n$ is $\boxed{46}$.
To find the smallest possible value of $n$ which is a four-digit positive integer such that dividing $n$ by $9$, the remainder is $5$, dividing $n$ by $7$, the remainder is $3$, and dividing $n$ by $5$, the remainder is $1$, follow these steps:
Step 1: Write down the congruences based on the given information.
$n \equiv 5 \pmod{9}$
$n \equiv 3 \pmod{7}$
$n \equiv 1 \pmod{5}$
Step 2: Use the Chinese Remainder Theorem (CRT) to solve the system of congruences. The CRT states that for pairwise coprime moduli, there exists a unique solution modulo their product.
Step 3: Compute the product of the moduli.
$M = 9 \times 7 \times 5 = 315$
Step 4: Compute the partial products.
$M_1 = M/9 = 35$
$M_2 = M/7 = 45$
$M_3 = M/5 = 63$
Step 5: Find the modular inverses.
$M_1^{-1} \equiv 35^{-1} \pmod{9} \equiv 2 \pmod{9}$
$M_2^{-1} \equiv 45^{-1} \pmod{7} \equiv 4 \pmod{7}$
$M_3^{-1} \equiv 63^{-1} \pmod{5} \equiv 3 \pmod{5}$
Step 6: Compute the solution.
$n = (5 \times 35 \times 2) + (3 \times 45 \times 4) + (1 \times 63 \times 3) = 350 + 540 + 189 = 1079$
Step 7: Check that the solution is a four-digit positive integer. Since 1079 is a three-digit number, add the product of the moduli (315) to the solution to obtain the smallest four-digit positive integer that satisfies the conditions.
$n = 1079 + 315 = 1394$
The smallest possible value of $n$ is 1394.
Visit here to learn more about Chinese Remainder Theorem:
brainly.com/question/30806123
#SPJ11
JEROME
(2/3)^2 = 2/9
can someone tell me what is Jerome mistake.
Answers
Law of Exponent
\( \displaystyle \large{( \frac{a}{b} )^{n} = \frac{ {a}^{n} }{ {b}^{n} } }\)
From the expression.
\( \displaystyle \large{( \frac{2}{3} )^{2} = \frac{ {2}^{2} }{ {3}^{2} } = \boxed{\frac{4}{9} } }\)
Jerome's mistake is that Jerome forgot to evaluate 2^2 or forgot to add 2^2. The denominator is correct but the numerator is wrong.
7. It costs $6 to get into the Carnival. Hotdogs cost $1.50 each, Hamburgers cost $1.75 each, French Fries cost $1.05 per
serving, Popcorn cost $1.15 per bag, and Soda is $.75 each. Each ride costs $2.00. How much money would you need to
get into the Carnival and to go on 8 rides, eat 2 hotdogs, 1 order of Fries, 2 bags of Popcorn, and 1 Soda?
Answers
Answer: $29.10
Step-by-step explanation:
1. Make a table, like the one shown in the image. You will need the item, its price, and how many are being bought.
2. Multiply the price and quantity of each item that is being bought.
3. Add all of the products together. This should get you the final price.
My steps are in the image. Hope this helps!

What sum is represented by the arrow diagram?

Answers
Answer:
Would it be 1?
Step-by-step explanation:
I'm not that sure but it seems it goes up to 4 so 4- -3 = 1. Exuse me if my wrong..
.Find dy/dx by implicit differentiation.y^5 +x^2y^3 = 1 +ye^x2
Answers
Answer:
(2xye^x² - 2xy³) / (5y^4 + 3y²x² - e^x²)
Step-by-step explanation:
differentiate each term:
d/dx (y^5) + d/dx (x² y³) = d/dx (1) + d/dx (ye^x²)
any time y is differentiated, make sure to include dy/dx:
5y^4 dy/dx + 2xy³ + 3y²x² dy/dx = 0 + e^x² dy/dx + 2xye^x²
collect terms with dy/dx:
dy/dx (5y^4 + 3y²x² - e^x²) = 2xye^x² - 2xy³
divide both sides by (5y^4 + 3y²x² - e^x²):
dy/dx = (2xye^x² - 2xy³) / (5y^4 + 3y²x² - e^x²)
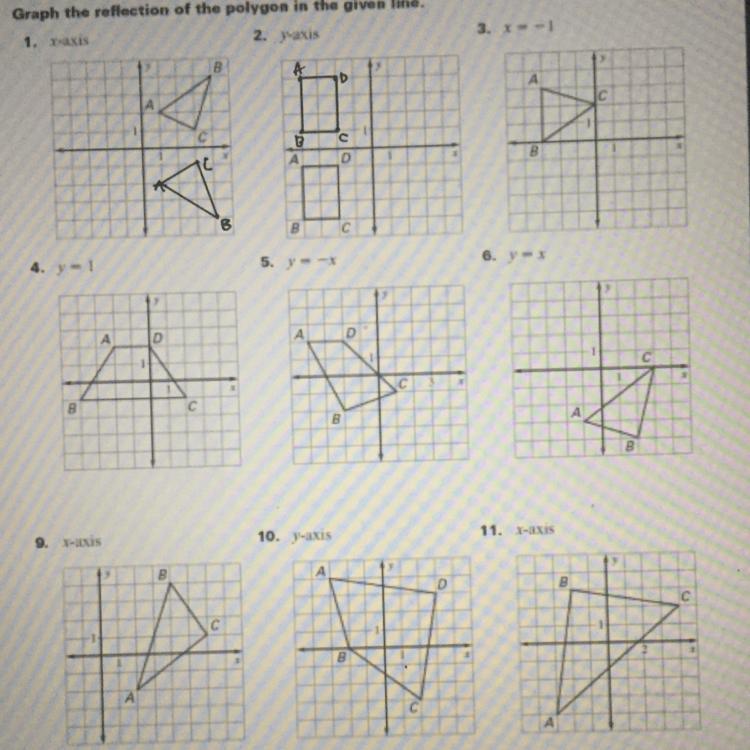
Reflections need help 1 and two already done just need help on 3-11
Answers
Step-by-step explanation:
-3 = -1
\(\frac{1}{2 } + (-3)\)
Answers
: Prove that a) X'Y' + X'Y +XY = X' +Y b) A'BC' + ABC' + BC'D = BC' Find the complement of the following function a) WX(Y'Z+YZ') + W'X'(Y' +Z)(Y+Z') b) (A+B'+C') (A'B' +C)(A + B'C') Find Dual of question 2 (a, b),
Answers
a) X'Y' + X'Y + XY simplifies to X' + Y.
b) A'BC' + ABC' + BC'D simplifies to BC'.
Complement of the functions:
a) Complement is W' + X' + YZ.
b) Complement is (A' + B + C)(A'B' + C' + A'B).
a) To prove X'Y' + X'Y + XY = X' + Y, we can use Boolean algebra identities:
X'Y' + X'Y + XY
= Y'(X' + X) + XY(Distributive Law)
= Y' + XY(X + X' = 1)
= X' + Y(Commutative Law)
Therefore, X'Y' + X'Y + XY simplifies to X' + Y.
b) To prove A'BC' + ABC' + BC'D = BC', we can simplify the expression using Boolean algebra:
A'BC' + ABC' + BC'D
= BC'(A' + A) + BC'D (Distributive Law)
= BC' + BC'D(A + A' = 1)
= BC'(BC' + BC'D = BC' + BC'(1) = BC')
Hence, A'BC' + ABC' + BC'D simplifies to BC'.
Complement of the given functions:
a) The complement of WX(Y'Z + YZ') + W'X'(Y' + Z)(Y + Z') is W' + X' + YZ.
b) The complement of (A + B' + C')(A'B' + C)(A + B'C') is (A' + B + C)(A'B' + C' + A'B).
Learn more About Distributive Law from the given link
https://brainly.com/question/25224410
#SPJ11
Solve for <1
<1= [?]
![Solve for <1 <1= [?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/fNh8op4l59FOTSLIvOuyn2FZ76lU1QfJ.png)
Answers
Step-by-step explanation:
∠1 + 49° + 49° = 180°
∠1 = 180-98
∠1 = 82°Does anyone can help me ? exercices 3 and 4

Answers
3) a) The domain of the rational function is x ≥ 1.
b) The domain of the rational function is all the real numbers except x = 3 and x = - 4.
4) a) The root of the rational function is 6.
b) The roots of the rational function are 4 and 1.
How to determine the domain and the roots of a rational function
Rational functions are algebraic expressions of the form P(x) / Q(x), where P(x) is the numerator and Q(x) is the denominator. 3) The domain of rational functions are the x-values that comprises P(x) except all values such that Q(x) = 0. Then, we proceed to find the domain of each function:
Case 1
The domain of P(x) = √(x - 1) is x ≥ 1 and the indetermination values of Q(x) = 2 · x is x = 0. Then, the domain of the rational function is x ≥ 1.
Case 2
The domain of P(x) = 3 is all the real numbers and the indetermination values of Q(x) = (x - 3) · (x + 4) are x = 3 and x = - 4. Then, the domain of the rational function is all the real numbers except x = 3 and x = - 4.
4) The roots of a function are all the values at which the function is evaluated such that is equal to zero.
Case 1
1 - 2 / (x - 4) = 0
[(x - 4) - 2] / (x - 4) = 0
x - 6 = 0
x = 6
The root of the rational function is 6.
Case 2
(x² - 5 · x + 4) / 5 = 0
x² - 5 · x + 4 = 0
(x - 4) · (x + 1) = 0
The roots of the rational function are 4 and 1.
To learn more on rational functions: https://brainly.com/question/8177326
#SPJ1
What mathematical term is used to designate a trapezoid (in the UK, a trapezium) having its two non-parallel sides of equal length? Such a shape is also sometimes referred to as a regular trapezoid?
Answers
The mathematical term used to designate a trapezoid (or trapezium in the UK) having its two non-parallel sides of equal length is an isosceles trapezoid.
The mathematical term used to designate a trapezoid having its two non-parallel sides of equal length is called an isosceles trapezoid or isosceles trapezium in the UK.
This shape is also sometimes referred to as a regular trapezoid, but the term "isosceles trapezoid" is more commonly used.
A trapezoid is a four-sided polygon that has two parallel sides and two non-parallel sides. The parallel sides of a trapezoid are called the bases, and the non-parallel sides are called the legs. The distance between the bases is called the height of the trapezoid.
The area of a trapezoid is given by:
Area = ((base1 + base2) x height) / 2
where base1 and base2 are the lengths of the two parallel sides, and height is the distance between the parallel sides.
Know more about trapezoid here:
https://brainly.com/question/1410008
#SPJ11
the midpoint of a class is the sum of its lower and upper limits divided by two. T/F
Answers
The midpoint of a class is indeed calculated by adding the lower and upper limits of the class and then dividing the sum by two. The statement is true.
This concept is commonly used in statistics and data analysis.
In statistical data, classes are often created to group data points within a range. Each class has a lower limit and an upper limit, defining the range of values it encompasses. The midpoint is a representative value within the class that provides a measure of its central tendency.
To calculate the midpoint, the lower and upper limits of the class are added together, resulting in the total range of the class. Dividing this sum by two gives the midpoint. It is important to note that the midpoint is not necessarily an actual data point; rather, it is a statistical measure used to represent the central value within a class.
For example, suppose we have a class with a lower limit of 10 and an upper limit of 20. Adding these values gives us 30, and dividing by two yields a midpoint of 15. This means that, for the purposes of analysis, we can consider the midpoint of the class as 15.
By calculating midpoints for each class in a data set, statisticians can summarize and analyze data in a more manageable and meaningful way. Midpoints help provide a sense of the central tendencies and distributions within the data, facilitating further statistical analysis and interpretation.
To know more about statistics and data analysis refer here:
https://brainly.com/question/30094945
#SPJ11
in a square garden plot (with an area of 400 sq ft)deer fencing priced at $1.50 per foot is to be installed around the plot. if sales tax is 7% how much will fencing price cost? (do not round)
Answers
We have a square garden of 400 square foot.
The area of a square is:
\(A=x^2\)where x: side length.
In this case:
\(\begin{gathered} A=400=x^2 \\ x=\sqrt[]{400}=20\text{ ft} \end{gathered}\)The perimeter of the square is the sum of the lengths of the sides of the square. As they are all equal, we can write:
\(P=4x=4\cdot20=80\text{ ft}\)The fencing is priced at $1.50 per foot. If we add the 7% sales tax to this price we get:
\(C=1.50\cdot(1+0.07)=1.50\cdot1.07=1.605\text{ \$/ft}\)The fencing will be installed in all the perimeter (80 ft).
We can calculate the total cost by multiplying the sales price ($1.605 per foot) and the perimeter (80 ft):
\(F=C\cdot P=1.605\frac{\text{\$}}{\text{ft}}\cdot80\text{ ft}=\$128.40\)Answer: the fencing will cost a total of $128.40
Find the slope of a line going through (0, 4) and (-2, 2).
Answers
Answer:
slope = 1
Slope-intercept form: y = 1x + 4
Step-by-step explanation:
Plot the 2 points on a graph. Count the rise and the run from point A to point B. From point A, you go down 2 and to the left 2 to get to point B. Meaning, the slope is -2 over -2. (-2/-2)What is -2 divided by -2? Positive 1 From there you can use the point-slope formula and find the slope-intercept form.Hope this helps!
how many solutions are there to square root x =9
Answers
Answer:
There are 2 solutions to square root x = 9
They are 3, and -3
Step-by-step explanation:
The square root of x=9 has 2 solutions,
The square root means, for a given number, (in our case 9) what number times itself equals the given number,
Or, squaring (i.e multiplying with itself) what number would give the given number,
so, we have to find the solutions to \(\sqrt{9}\)
since we know that,
\((3)(3) = 9\\and,\\(-3)(-3) = 9\)
hence if we square either 3 or -3, we get 9
Hence the solutions are 3, and -3
I've only touched on this topic and need a better explanation. Please!!!

Answers
12, 13, 15, 19 are the first four terms of the sequence aₙ = 2aₙ₋₁ - 11
a₁ = 12
aₙ = 2aₙ₋₁ - 11 for n≥2
We have to find the first four terms of the sequence
a₂ = 2a₂₋₁ - 11
=2a₁-11
=2(12)-11
a₂=24-11 = 13
Now let us find a₃
a₃=2a₂-11
=2(13)-11= 26-11
a₃ = 15
a₄=2a₃-11
=2(15)-11 = 19
Hence, 12, 13, 15, 19 are the first four terms of the sequence aₙ = 2aₙ₋₁ - 11
To learn more on Sequence click:
https://brainly.com/question/21961097
#SPJ1
What I'd the value of x
Answers
Answer:
Can you please give us figure so that i can help you
help i will make u a brainllest 17. Which statement is true? 11. If m




Answers
Answer:
17. D
11. 147 deg
Last problem: 2nd answer
Step-by-step explanation:
17. D
All parallelograms have 4 sides, so all parallelograms are quadrilaterals.
11.
m<B = m<D = 33
m<A + m<B + m<C + m<D = 360
m<A + 33 + m<C + 33 = 360
m<A + m<C = 294
m<A = m<C = (1/2) * 294
m<C = 147
Last problem:
If in a quadrilateral, a pair of opposite sides is both parallel and congruent, then the quadrilateral is a parallelogram. In the second choice, the same pair of sides is parallel and congruent, so this is the answer.
with a reserve requirement of 5% and an initial deposit of $400, what is the maximum total amount of money that will be in the money supply? assume that all currency is deposited in a bank 7 banks hold no excess reserves (rr=.05)
Answers
The maximum money supply with a 5% reserve requirement and a $400 initial deposit is $8,000.
How to find maximum money?To calculate the maximum total amount of money that will be in the money supply, we need to consider the money multiplier effect based on the reserve requirement.
The money multiplier is given by the formula: MM = 1 / reserve requirement.
Given that the reserve requirement is 5% (rr = 0.05), the money multiplier is MM = 1 / 0.05 = 20.
The initial deposit is $400.
To calculate the maximum total amount of money in the money supply, we multiply the initial deposit by the money multiplier:
Maximum Money Supply = Initial Deposit * Money Multiplier
= $400 * 20
= $8,000.
Therefore, the maximum total amount of money that will be in the money supply is $8,000 when the reserve requirement is 5% and all currency is deposited in banks with no excess reserves.
Learn more about money
brainly.com/question/2696748
#SPJ11
A cell phone tower casts a 100 foot shadow.At the same time, a 4 ft 6 inch post near the tower casts a shadow of 3 ft 4 inches. What is the height of the tower? Please help I need an answer ASAP
Answers
Answer:
https://brainly.com/question/11428290
Step-by-step explanation:
You can go to this webpage and see if you find what you are looking for. :)
250 ft.
3ft 4in = 4ft 6in - 1ft 2in.
i dunno how to explain it any better. lol sorry.
For each figure, complete the statement a/b = ?/?.

Answers
Answer:
b/c
Step-by-step explanation:
a/b is the equivalent of b/c, sorry if this is incorrect.