a real number $a$ is chosen randomly and uniformly from the interval $[-20, 18]$. the probability that the roots of the polynomial $x^4 2ax^3 (2a - 2)x^2 (-4a 3)x - 2$ are all real can be written in the form $\dfrac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. find $m n$.
Answers
Since, m and n are prime positive number. Therefore,
m + n = 18 + 19 =037
The polynomial we are given is rather complicated, so we could use Rational Root Theorem to turn the given polynomial into a degree-2 polynomial. With Rational Root Theorem, x = 1, -1, 2, -2 are all possible rational roots. Upon plugging these roots into the polynomial, x = -2 and x = 1 make the polynomial equal 0 and thus, they are roots that we can factor out.
The polynomial becomes:
(x - 1)(x + 2)(x^2 + (2a - 1)x + 1)
Since we know 1 and -2 are real numbers, we only need to focus on the quadratic.
We should set the discriminant of the quadratic greater than or equal to 0.
(2a - 1)^2 - 4 ≥ 0.
This simplifies to:
a ≥ 3/2
or,
a ≤ - 1/2
This means that the interval (- 1/2 ,3/2) is the "bad" interval. The length of the interval where a can be chosen from is 38 units long, while the bad interval is 2 units long. Therefore, the "good" interval is 36 units long.
36/38 = 18/19
18+ 19 = 037
Learn more about Prime Positive Number :
https://brainly.com/question/24635729
#SPJ4
Related Questions
2. Change the fraction to a decimal
A 6/100
B 43/100
C 3/10
D 4 23/ 1,000
Answers
Answer:
A. 0.06
B. 0.43
C. 0.3
D. 4.023
this might help you
1/4 becomes 1 ÷ 4 because they are the same meaning
1/4 = 0.25
1 ÷4 = 0.25
I NEED AN ANSWER PLEASE :(((

Answers
Answer:
80 lemons
Step-by-step explanation:
Let x represent the amount of lemons that were on the tree.
We can use this to set up an equation:
\(40\%x=32\)
Note that percentages can also be written as that number over 100.
\(\frac{40}{100}x=32\)
Simplify the fraction.
\(\frac{2}{5}x=32\)
Multiply both sides by 5
\(2x=160\)
Divide both sides by 2
\(x=80\)
There were 80 lemons on the tree before he picked the lemons.
10) An architect is considering bidding for the design of a new shopping mall. The cost of drawing plans
and submitting a model is $10,000. The probability of being awarded the bid is 0.09, and anticipated
profits are
$100,000, resulting in a possible gain of this amount minus the $10,000 cost for plans and a
model. What is the expected value in this situation? Answers without any work shown will
receive no credit.
A) $8000
B) $9000
C) -$1000
D) $8100
Answers
Answer:
-$1000
Step-by-step explanation:
Given that:
Possible gain = 100,000 - 10,000 = 90,000
Loss =. 10,000 = cost of model submission
P(being awarded) = 0.09
P(not being awarded). = 1 - 0.09 = 0.91
X : 90000 _____ - 10,000
P(x) : 0.09 _______ 0.91
Expected value :
Σx*p(x) = (90000*0.09) + (-10,000 * 0.91)
= 8100 - 9100
= - 1000
find the perimeter of ABC with vertices A(-4,4), B(2,-2), and C(-4,-2). Round your answer to the nearest hundredth.
Answers
The perimeter of ABC with vertices A(-4,4), B(2,-2), and C(-4,-2) is 20.848 units.
We are given the vertices:
A(-4,4), B(2,-2), and C(-4,-2).
We need to find the perimeter of ABC.
AB = √ ( 2 + 4)² + (-2 - 4)²
AB = √ 6² + 6²
AB = √72
AB = 6 √2 units
BC = √ (-4 - 2)² + ( -2 + 2)²
BC = √ 6²
BC = 6 units
AC = √ ( -4 + 4)² + (-2 - 4)²
AC = √ 6²
AC = 6 units.
Perimeter = AB + BC + AC
Perimeter = 6 √2 + 6 + 6 units
Perimeter = 12 + 6 √2 units.
Perimeter = 12 + 6(1.414) units
Perimeter = 12 + 8.848 units
Perimeter = 20.848 units
Therefore, the perimeter of ABC with vertices A(-4,4), B(2,-2), and C(-4,-2) is 20.848 units.
Learn more about perimeter here:
https://brainly.com/question/24571594
#SPJ9
b) A factor of 30 is chosen at random.
What is the probability, as a decimal, that it is a 2-digit number?
Answers
Answer:
0.375
Step-by-step explanation:
Factors of 30: 1, 2, 3, 5, 6, 10, 15 and 30
three two digit numbers and 8 total so 3/8
x to the power of 2 plus y to the power of 2
x=2
y=3

Answers
Answer:
49
Step-by-step explanation:
(2^2 + 3)^2
(4 + 3)^2
(7)^2
49
Yk cause of bidams you gotta do 2 to the power of 2 first, and then get 4 + 3. Then you add them, you get 7. Cube it and get 49. Ez ;>
*winks and runs off*
Does lim 2x+y (x,y) → (0,0) x2 +xy4 + 18 the limit exist?"
Answers
To determine if the limit of the function f(x, y) = 2x + y as (x, y) approaches (0, 0) exists, we need to evaluate the limit expression and check if it yields a unique value.
We can evaluate the limit by approaching (0, 0) along different paths. Let's consider two paths: the x-axis (y = 0) and the y-axis (x = 0).
For the x-axis approach, we substitute y = 0 into the function f(x, y):
lim(x,y→(0,0)) 2x + y = lim(x→0) 2x + 0 = lim(x→0) 2x = 0.
For the y-axis approach, we substitute x = 0 into the function f(x, y):
lim(x,y→(0,0)) 2x + y = lim(y→0) 2(0) + y = lim(y→0) y = 0.
Since the limit along the x-axis approach is 0 and the limit along the y-axis approach is also 0, we might conclude that the limit of f(x, y) as (x, y) approaches (0, 0) is 0. However, this is not the case.
Consider the path y = x^2. Substituting this into the function f(x, y):
lim(x,y→(0,0)) 2x + y = lim(x→0) 2x + x^2 = lim(x→0) x(2 + x) = 0.
This shows that along the path y = x^2, the limit is 0. However, since the limit of f(x, y) depends on the path of approach (in this case, the limit is different along different paths), we conclude that the limit does not exist as (x, y) approaches (0, 0).
To learn more about function click here :
brainly.com/question/31062578
#SPJ11
What is the first step to conducting a statistical study?.
Answers
The first step to conducting a statistical study is to clearly define the research question or problem.
This involves identifying the population of interest, the variables to be measured, and the hypothesis or objective of the study. Once the research question is clearly defined, the next step is to design the study, including selecting an appropriate sample size, choosing a sampling method, and determining the data collection method.
It is also important to consider potential sources of bias and confounding factors that may impact the study results. Overall, a well-designed statistical study should be able to produce reliable and accurate results that can be used to draw meaningful conclusions about the population of interest.
To know more about statistical study:
https://brainly.com/question/23276495
#SPJ4
what population and sample? sixty employees from a firm of 4500 employees are randomly selected to be on a committee to evaluate how to implement sensitivity training. currently, training is done in person, but a proposal has been made to implement the required training online. each of the committee members is asked to vote yes or no on the proposal.
Answers
The population in this scenario consists of all employees in the firm, which totals 4,500 individuals. The sample is a subset of the population, specifically 60 randomly selected employees who are part of a committee evaluating the implementation of sensitivity training.
the population refers to the entire group of employees in the firm, which consists of 4,500 individuals. The sample, on the other hand, is a smaller group of 60 employees who have been randomly selected to form a committee. This committee's purpose is to evaluate the proposal of implementing sensitivity training online instead of the current in-person format.
The sample of 60 employees is chosen in a random manner to ensure representativeness and minimize potential bias. By selecting a subset of the population, the committee can provide insights and perspectives that are representative of the larger employee base. Each committee member will have the opportunity to vote "yes" or "no" on the proposal, and their votes will be used to determine the overall sentiment of the committee regarding the implementation of online sensitivity training.
It's important to note that the sample of 60 employees is being used as a representative group to make inferences about the entire population.
Learn more about population here:
https://brainly.com/question/31598322
#SPJ11
3x + 5 - (5x + 8) = -4x - 7
Answers
Answer:
Standard form:
2x + 4 = 0
Factorization:
2(x + 2) = 0
Solutions:
x = −4 /2 = −2
Answer:
x = -2
Step-by-step explanation:
Step 1: Simplify both sides of the equation.
3x+5−(5x+8)=−4x−7
3x+5+−1(5x+8)=−4x−7(Distribute the Negative Sign)
3x+5+−1(5x)+(−1)(8)=−4x−7
3x+5+−5x+−8=−4x−7
3x+5+−5x+−8=−4x+−7
(3x+−5x)+(5+−8)=−4x−7(Combine Like Terms)
−2x+−3=−4x−7
−2x−3=−4x−7
Step 2: Add 4x to both sides.
−2x−3+4x=−4x−7+4x
2x−3=−7
Step 3: Add 3 to both sides.
2x−3+3=−7+3
2x=−4
Step 4: Divide both sides by 2.
\(\frac{2x}{2} = \frac{-4}{2}\)
x = −2
find a polynomial function of lowest degree with rational coefficients that has the given numbers as some of its zeros.
Answers
In a polynomial function of the lowest degree with rational coefficients that have the given numbers as some of its zeros, we can use the fact that if a number "a" is a zero of a polynomial function, then (x-a) is a factor of the function.
Therefore, we can start by multiplying together (x-a) for each given zero, and then simplify the resulting expression to get the polynomial function in standard form with rational coefficients.
For example, if the given zeros are 2, -1, and 1/2, we would start by multiplying (x-2)(x+1)(x-1/2), which gives:
(x-2)(x+1)(2x-1)
Expanding this expression, we get:
2x^3 - 3x^2 - 5x + 2
This is a polynomial function of degree 3 (highest exponent is 3) with rational coefficients (all coefficients are integers or fractions). Note that this is the lowest degree possible for a polynomial with these zeros, since there are three distinct zeros.
Learn more about rational here:
https://brainly.com/question/1310146
#SPJ11
Find the perimeter of the figure

Answers
Answer: 30
Step-by-step explanation: 6 + 4 + 4 + 9.5 + 6 + 6.5 = 30
8x + 7 = -25
What is the solution for this equation?
Answers
8x + 7 = -25
=> 8x = -25 - 7 = -32
=> x = -32/8 = -4
Answer:
-4=x
Step-by-step explanation:
8x+7(-7)=-25(-7)
8x(/8)=-32(/8)
-4=x
• Problem 1. (a). Prove that the empty set 0 is not NP-complete. (b). Prove that if P=NP, then every language A EP, except A = 0 and A= = *, is NP-complete.
Answers
To prove that the empty set 0 is not NP-complete, we need to show that 0 is not in NP or that no NP-complete problem can be reduced to 0.
Since 0 is a language that does not contain any strings, it is trivially decidable in constant time. Therefore, 0 is in P but not in NP.
Since no NP-complete problem can be reduced to a problem in P, it follows that 0 is not NP-complete.
(b) To prove that if P=NP, then every language A EP, except A = 0 and A= = *, is NP-complete, we need to show that if P=NP, then every language A EP can be reduced to any NP-complete problem.
Assume P=NP. Let L be an arbitrary language in EP. Since P=NP, there exists a polynomial-time algorithm that decides L. Let A be an NP-complete language. Since A is NP-complete, there exists a polynomial-time reduction from any language in NP to A.
To show that L can be reduced to A, we construct a reduction as follows: given an instance x of L, use the polynomial-time algorithm that decides L to determine whether x is in L. If x is in L, then return a fixed instance y of A. Otherwise, return the empty string.
This reduction takes polynomial time since the algorithm for L runs in polynomial time, and the reduction itself is constant time. Therefore, L is polynomial-time reducible to A.
Since A is NP-complete, any language in NP can be reduced to A. Therefore, if P=NP, then every language in EP can be reduced to any NP-complete problem except 0 and * (which are not in NP).
Know more about NP-complete problem here:
https://brainly.com/question/29979710
#SPJ11
find the equation of the tangent plane to f(x, y) = x2 − 2xy 3y2 having slope 6 in the positive x direction and slope 2 in the positive y direction.
Answers
The equation of the tangent plane to f(x, y) = x^2 − 2xy + 3y^2 with slopes 6 in the positive x direction and 2 in the positive y direction is 6x - 2y - 10 = 0.
To find the equation of the tangent plane to the surface defined by f(x, y) = x^2 − 2xy + 3y^2, we need to determine the normal vector of the plane at a given point.
The gradient of the function f(x, y) gives the direction of the steepest ascent at any point. Therefore, the gradient vector will be orthogonal to the tangent plane.
The gradient of f(x, y) is given by:
∇f(x, y) = (2x - 2y, -2x + 6y)
We want the tangent plane to have a slope of 6 in the positive x direction and a slope of 2 in the positive y direction. This means that the direction vector of the plane is orthogonal to the gradient vector and has components (6, 2).
Since the normal vector of the plane is orthogonal to the direction vector, it will have components (-2, 6).
At a given point (x₀, y₀) on the surface, the equation of the tangent plane can be written as:
-2(x - x₀) + 6(y - y₀) = 0
Expanding and simplifying, we get:
-2x + 2x₀ + 6y - 6y₀ = 0
Rearranging, we obtain:
-2x + 6y - (2x₀ - 6y₀) = 0
Comparing this with the equation of the tangent plane 6x - 2y - 10 = 0, we find that x₀ = -5 and y₀ = -1.
Therefore, the equation of the tangent plane to f(x, y) = x^2 − 2xy + 3y^2 with slopes 6 in the positive x direction and 2 in the positive y direction is 6x - 2y - 10 = 0.
Visit here to learn more about the tangent plane:
brainly.com/question/31433124
#SPJ11
are we confident that the percentage of contra costa county residents that supports a ban is greater than the percentage nationwide as reported by the pew research center? why or why not?
Answers
To determine if the percentage of Contra Costa County residents supporting a ban is greater than the nationwide percentage reported by the Pew Research Center, we need to follow these steps.
1. Obtain the Pew Research Center's report on the nationwide percentage of people supporting a ban.
2. Gather data on the percentage of Contra Costa County residents supporting the ban. This data could come from local surveys, polls, or other relevant sources.
3. Compare the two percentages to see if the Contra Costa County percentage is greater than the nationwide percentage.
If the Contra Costa County percentage is greater than the nationwide percentage, we can be confident that a higher proportion of county residents support the ban. However, it is important to note that survey results may vary based on the sample size, methodology, and timing of the polls. To draw more accurate conclusions, it's essential to consider multiple sources of data and ensure the reliability of the information being used.
In summary, to confidently assert that the percentage of Contra Costa County residents supporting a ban is greater than the nationwide percentage, we must gather local data and compare it to the Pew Research Center's report. The reliability of this conclusion depends on the accuracy and representativeness of the data used.
To know more about Percentage visit:
https://brainly.com/question/32197511
#SPJ11
Find (and classify) the critical points of the following function and determine if they are local max, local min, or neither: f(x) =x^4 - 2x^2
Answers
Solution:
Given:
\(f(x)=x^4-2x^2\)To get the local maximum and minimum point, we differentiate the function twice.
\(\begin{gathered} f^{\prime}(x)=4x^3-4x \\ \\ To\text{ get the critical points, f'(x)=0} \\ 4x^3-4x=0 \\ \text{Factorizing,} \\ 4x(x^2-1)=0 \\ \text{Thus,} \\ (4x)(x-1)(x+1)=0 \\ \text{Hence, the critical points are;} \\ x=0,x=1,x=-1 \end{gathered}\)To get the maximum and minimum points, we differentiate further,
\(\begin{gathered} f^{\prime}(x)=4x^3-4x \\ f^{\doubleprime}(x)=12x^2-4 \\ \\ \text{Inputting the critical points into f''(x),} \\ \text{when x = -1,} \\ f^{\doubleprime}(-1)=12(-1)^2-4=12-4=8 \\ S\text{ ince f''(x)>0, then this is a minimum point.} \\ x=-1\text{ is a minimum} \\ \\ \\ \text{when x = 1,} \\ f^{\doubleprime}(1)=12(1^2)-4=12-4=8 \\ S\text{ ince f''(x)>0, then this is a minimum point.} \\ x=1\text{ is a minimum} \\ \\ \text{when x = 0,} \\ f^{\doubleprime}(0)=12(0^2)-4=0-4=-4 \\ S\text{ ince f''(x)<0, then this is a maximum point.} \\ x=0\text{ is a maximum} \end{gathered}\)Thus,
\(\begin{gathered} At\text{ x = 0,} \\ f(x)=x^4-2x^2 \\ f(0)=0^4-2(0^2)=0-0=0 \\ \\ \text{Hence, (0,0) is a local maximum} \\ \\ \\ At\text{ x = -1,} \\ f(x)=x^4-2x^2 \\ f(-1)=(-1)^4-2(-1)^2=1-2=-1 \\ \\ \text{Hence, (-1,-1) is a local minimum} \\ \\ \\ At\text{ x = 1,} \\ f(x)=x^4-2x^2 \\ f(1)=1^4-2(1^2) \\ f(1)=1-2=-1 \\ \\ \text{Hence, (1,-1) is a local minimum} \end{gathered}\)The graph is as shown below;
Therefore,
The local minimum occurs at (-1,-1) and (1,-1)
The local maximum occurs at (0,0)

student has only a few hours to prepare for two different exams this afternoon. The above table shows alternative possible exam scores with three alternative uses of he student's time. What is the opportunity cost of scoring a 94 on the economics exam rather than a 77 ? Please explain - show the numeric points of opportunity cost and explain you reasoning.
Answers
Opportunity cost of scoring 94 instead of 77 = Benefit of scoring 77 - Benefit of scoring 94
Since the table you mentioned is not provided, I'll assume the table represents the possible exam scores for the student in economics and another subject, let's say mathematics. Let's consider the following scenario:
Economics Exam Scores:
Scoring a 94: 5 hours of study
Scoring a 77: 3 hours of study
Mathematics Exam Scores:
Scoring a 92: 6 hours of study
Scoring an 80: 2 hours of study
To calculate the opportunity cost, we compare the benefit (exam score) of one option with the benefit of the next best alternative. In this case, we compare the benefits of scoring a 94 in economics with scoring a 77 in economics.
Opportunity cost = Benefit of the Next Best Alternative - Benefit of the Chosen Option
For the economics exam:
Opportunity cost of scoring 94 instead of 77 = Benefit of scoring 77 - Benefit of scoring 94
The benefit of scoring 77 in economics is the difference in study time between scoring 77 and scoring 94, which is 5 hours - 3 hours = 2 hours.
Therefore, the opportunity cost of scoring a 94 on the economics exam instead of a 77 is 2 hours of study time.
The concept of opportunity cost helps us understand the value of the next best alternative foregone. In this case, the student could have spent those 2 additional hours studying mathematics, which may have resulted in a higher score in that subject.
learn more about value here:
https://brainly.com/question/30145972
#SPJ11
Consider the following three systems of linear equations. System A System B System C 11 x= -44 [B1] x=-4 [C1] - 7x- 6y= 10 [A1] 6x+2y=- 18 [A2] 6x + 2y=-18 [B2] 6x +2y=-18 [C2] Answer the questions below. For each, choose the transformation and then fill in the blank with the correct number. The arrow ( - ) means the expression on the left becomes the expression on the right. How do we transform System A into System B? O X Equation [A1] → Equation [B1] Х ? 1 x Equation [A2] → Equation [B2] * Equation [A1] + Equation [A2] → Equation [B2] 1 x Equation [A2] + Equation [A1] → Equation [31] How do we transform System B into System C? 1 x Equation (B1] Equation (C1] X Equation [B2] → Equation (C2] 1 x Equation [31] + Equation [B2] → Equation (C2] * Equation [B2] + Equation [31] → Equation [21]
![Consider the following three systems of linear equations. System A System B System C 11 x= -44 [B1] x=-4](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/PQ3XhOzVnUa8bsdvqWit2CLqvadDRkTl.png)
Answers
The correct transformations:
1) 3 x Equation [A2] + Equation [A1] → Equation [B1]
2). 1/11 x Equation [B1} → Equation [C1]
The correct options are D and A respectively.
What is the system of equations?One or many equations having the same number of unknowns that can be solved simultaneously are called simultaneous equations. And the simultaneous equation is the system of equations.
Given:
We have three systems of linear equations.
To transform system A into system B:
Multiply 3 to the equation A2 and then add to equation A1,
we get,
-7x +18x -6y + 6y = 10- 54
11x = -44
equation B1.
To transform system B into system C:
Multiply 1/11 to equation B1,
we get,
x = -4
equation C1.
Therefore, the transformations are given above.
To learn more about the system of equations;
brainly.com/question/13729904
#SPJ1
The following table contains the probability distribution for X = the number of traffic accidents reported in a day in Corvallis, Oregon.
X 0 1 2 3 4 5
P(X) 0.10 0.20 0.45 0.15 0.05 0.05
a. What is the probability of 3 accidents?
b. What is the probability of at least 1 accident?
c. What is the expected value (mean) of the number of accidents?
d. What is the variance of the number of accidents?
e. What is the standard deviation of the number of accidents?
Answers
a. The probability of 3 accidents is P(X=3) = 0.15.
b. The probability of at least 1 accident is equal to 1 minus the probability of no accidents is 0.90.
c. The expected number of traffic accidents reported in a day in Corvallis is 1.95.
d. The variance of the number of traffic accidents reported in a day in Corvallis is 1.6525.
e. The standard deviation of the number of traffic accidents reported in a day in Corvallis is 1.284.
a. The probability of 3 accidents is P(X=3) = 0.15.
b. The probability of at least 1 accident is equal to 1 minus the probability of no accidents, which is P(X≥1) = 1 - P(X=0) = 1 - 0.10 = 0.90.
c. The expected value (mean) of the number of accidents is calculated as the sum of the products of the possible values of X and their probabilities, which is:
E(X) = 0(0.10) + 1(0.20) + 2(0.45) + 3(0.15) + 4(0.05) + 5(0.05) = 1.95.
Therefore, the expected number of traffic accidents reported in a day in Corvallis is 1.95.
d. The variance of the number of accidents is calculated as the sum of the squares of the differences between each possible value of X and the expected value, weighted by their probabilities, which is:
Var(X) = [ (0-1.95)²(0.10) + (1-1.95)²(0.20) + (2-1.95)²(0.45) + (3-1.95)²(0.15) + (4-1.95)²(0.05) + (5-1.95)²(0.05) ]
= 1.6525.
Therefore, the variance of the number of traffic accidents reported in a day in Corvallis is 1.6525.
e. The standard deviation of the number of accidents is the square root of the variance, which is:
SD(X) = √(1.6525) = 1.284.
Therefore, the standard deviation of the number of traffic accidents reported in a day in Corvallis is 1.284.
To learn more about Probability here:
brainly.com/question/30034780#
#SPJ11
a pharmaceutical company knows that five percent of all users of a certain drug experience a serious side effect. a researcher examines a sample of 200 users of the drug. a. what is the probability of finding between 8 and 12 cases with side effects? (round final answer to 4 decimal places.) b. what is the probability of finding more than 16 cases with side effects? (round final answer to 4 decimal places.)
Answers
Using the normal distribution, the probabilities are given as follows:
a. Between 8 and 12 cases with side effects: 0.582 = 58.2%.
b. More than 16 cases with side effects: 0.0174 = 1.74%.
Normal Probability DistributionThe z-score of a measure X of a normally distributed variable that has mean represented by \(\mu\) and standard deviation represented by \(\sigma\) is given by the equation presented below:
\(Z = \frac{X - \mu}{\sigma}\)
The z-score measures how many standard deviations the measure X is above or below the mean of the distribution, depending if the z-score is positive or negative.From the z-score table, the p-value associated with the z-score is found, and it represents the percentile of the measure X in the distribution.The binomial distribution is the probability of x successes on n trials, with p probability of a success on each trial. It can be approximated to the normal distribution with \(\mu = np, \sigma = \sqrt{np(1-p)}\).The parameters for the binomial distribution in this problem are given as follows:
p = 0.05, n = 200.
Hence the mean and the standard deviation of the approximation are given as follows:
E(X) = np = 200 x 0.05 = 10.\(\sqrt{V(X)} = \sqrt{np(1 - p)} = \sqrt{200(0.05)(0.95)} = 3.08\)For item a, using continuity correction, the probability of between 8 and 12 cases with side effects is the p-value of Z when X = 12.5 subtracted by the p-value of Z when X = 7.5, hence:
X = 12.5:
\(Z = \frac{X - \mu}{\sigma}\)
Z = (12.5 - 10)/3.08
Z = 0.81
Z = 0.81 has a p-value of 0.7910
X = 7.5:
\(Z = \frac{X - \mu}{\sigma}\)
Z = (7.5 - 10)/3.08
Z = -0.81
Z = -0.81 has a p-value of 0.2090.
0.7910 - 0.2090 = 0.582 probability.
For item b, the probability of finding more than 16 cases with side effects is one subtracted by the p-value of Z when X = 16.5, hence:
\(Z = \frac{X - \mu}{\sigma}\)
Z = (16.5 - 10)/3.08
Z = 2.11
Z = 2.11 has a probability of 0.9826.
1 - 0.9826 = 0.0174 = 1.74% probability.
A similar problem, also given about the normal distribution, is given at https://brainly.com/question/4079902
#SPJ1
Find the distance between the two points in simplest radical form.
Can someone helps me I’ll give u a cookie :)

Answers
Answer:
\(d=\sqrt{58}\approx7.6\)
Step-by-step explanation:
To find the distance between any two points, we can use the distance formula:
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2\)
Our first point, A, is at (1, 1) and our second point, B, is at (-2, 8).
Let's let A(1, 1) be (x₁, y₁) and B(-2, 8) be (x₂, y₂). Substitute this into the distance formula:
\(d=\sqrt{(-2-1)^2+(8-1)^2\)
Subtract:
\(d=\sqrt{(-3)^2+(7)^2\)
Square:
\(d=\sqrt{9+49}\)
Add:
\(d=\sqrt{58}\)
This cannot be simplified.
So, the distance between the two points is √58 or about 7.6 units.
And we're done!
So... where's my cookie :)?
don’t mind the 28, i literally have no idea. pls help ^^^ thx <3

Answers
9514 1404 393
Answer:
(d) 28
Step-by-step explanation:
When you are asked to evaluate g(n) for some value of n, put that value where n is and do the arithmetic.
g(n) = 3n -2
g(10) = 3·10 -2
= 30 -2 = 28
HELP ME PLS
The line of best fit is shown on the scatter plot below. What is the equation of the line of best fit?

Answers
Answer:
D
Step-by-step explanation:
Notice how it goes down one unit and right one unit. Thats how you get the slope (-x) and then then the +9 is the intercept of the y-axis which you can see is where the graph is starting here.
What is the area of this plane figure?
45 square centimeters
50 square centimeters
65 square centimeters
90 square centimeters
Answers
Answer:
it would be nice if I could see it
1 Apply Malcolm is making chicken rice soup. The recipe calls for 5 cups of chicken broth per cup of brown rice. How many cups of brown rice are needed for 20 cups of chicken broth? Explain how you know.
Answers
Answer:
you will need 4 cups of brown rice because it says per cup of brown rice
Step-by-step explanation:
ok so,
5 cups of chicken broth= 1 cup of brown rice
so if there's 20 cups of chicken broth, then:
20/5(since 5 equals 1 cup of brown rice)
=4 cups of brown rice
Which scatterplot has a correlation coefficient closest to r = -1?
Answers
Step-by-step explanation:
negative correlation because the negative correlation moves towards the left.
help plzzz get brainlyest!!!!!!

Answers
Answer:
Plan C
Step-by-step explanation:
sorry if i'm wrong
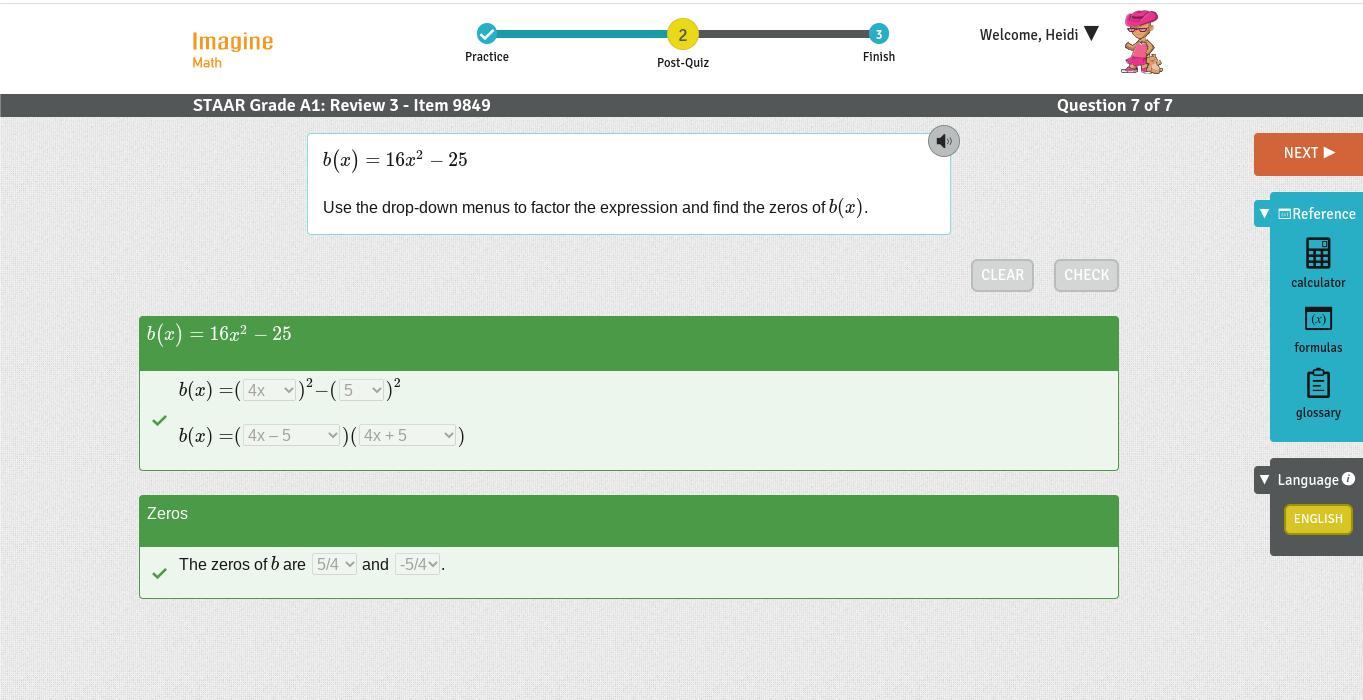
Solve b(x)=16x2−25 to find the zeroes of b(x)
Answers
Answer:
5/4 and -5/4
Step-by-step explanation:
Solve means change b(x) to 0, factor and use zero product property (write two smaller equations)
This equation is a "difference of two squares" or "difference of perfect squares"
b(x) = 16x^2 - 25
0 = (4x - 5)(4x + 5)
Make two smaller equations.
4x-5=0 and 4x+5=0
Solve both of these separately.
4x - 5 = 0
add 5
4x = 5
divide by 4
x = 5/4 and,
4x + 5 = 0
subtract 5
4x = -5
divide by 4
x = -5/4
"zeros" are solutions are roots, are x-intercepts. These are all pretty commonly interchangeable. (Not exactly, technically for a mathematician) But for a student knowing what to do with a question, for all these:
find zeros
find solutions
find roots
find x-intercepts
Set it equal to 0 and solve.
The zeros are 5/4 and -5/4
Answer:
b(x)= (4x)^2-(5)^2
b(x)=(4x-5)(4x+5)
The zeros of b are 5/4 and -5/4
Question Content Area At XLT Inc., variable costs are $80 per unit, and fixed costs are $40,000. Sales are estimated to be 4,000 units. a. If the company switches from a plan to produce 8,000 units to a plan to produce 10,000 units, absorption costing operating income would by $fill in the blank 2 . b. How much would variable costing operating income differ between the two production plans?
Answers
a. Switching from a production plan of 8,000 units to a plan of 10,000 units would result in an absorption costing operating income of $fill in the blank 2.
b. The difference in variable costing operating income between the two production plans can be calculated based on the change in the number of units produced.
a. To determine the absorption costing operating income, we need to consider both the fixed and variable costs. In absorption costing, fixed costs are allocated to each unit produced, while variable costs are directly attributed to the units. Given that the fixed costs are $40,000 and the variable cost per unit is $80, we can calculate the absorption costing operating income for each production plan
For the initial plan of 8,000 units:
Total fixed costs = $40,000
Total variable costs = 8,000 units * $80 per unit = $640,000
Total costs = Total fixed costs + Total variable costs = $40,000 + $640,000 = $680,000
For the revised plan of 10,000 units:
Total fixed costs remain the same at $40,000
Total variable costs = 10,000 units * $80 per unit = $800,000
Total costs = Total fixed costs + Total variable costs = $40,000 + $800,000 = $840,000
Absorption costing operating income = Sales - Total cost
b. Variable costing operating income differs between the two production plans as it only considers the variable costs directly associated with the units produced. In variable costing, fixed costs are treated as period costs and are not allocated to the units.
For the initial plan of 8,000 units:
Total variable costs = 8,000 units * $80 per unit = $640,000
For the revised plan of 10,000 units:
Total variable costs = 10,000 units * $80 per unit = $800,000
The difference in variable costing operating income between the two plans would be $800,000 - $640,000 = $160,000.
Learn more about number here:
https://brainly.com/question/3589540
#SPJ11