A quadrilateral is graphed on a coordinate grid and then translated 1 unit to the left and 8 units up. If one of the vertices of the original quadrilateral is located at (-5, 6), what is the ordered pair of this vertex of the new quadrilateral after the translation?

Answer:

its sophisticated but answer is 3

Step-by-step explanation:

you have to dive deep into it and research

When substituting y = 11 into the equation y = 1/2(x) - 25, we find that x = 72, confirming that (23.5, 11) is a valid point of intersection.

Given that x is 23.5, it is required to prove that it is an intersection point for the equation y = 1/2(x) - 25 when y is equal to 11.

The equation is given as y = 1/2(x) - 25

When y = 11, we can substitute the value of y in the equation to obtain 11 = 1/2(x) - 25

This can be simplified as 11 + 25 = 1/2(x)36 = 1/2(x)

On solving, x = 72Thus, when y is equal to 11 and x is equal to 72, the given point of intersection is valid.

Therefore, it can be concluded that x = 23.5 is a point of intersection for the equation y = 1/2(x) - 25 when y is equal to 11.

In summary, when given an equation with two variables, we can find the point of intersection by setting one of the variables to a given value and solving for the other variable. In this case, when y is equal to 11, we can solve for x and obtain the point of intersection as (72,11).

For more questions on intersection

https://brainly.com/question/30429663

#SPJ8

Answer:

y=-1/4x+5/4

Step-by-step explanation:

M is equal to the X in the middle of the equation. B is equal to the Y Intercept. Hope this helps! If you're still having trouble understanding this, I would look up "Slope Intercept Equations" on (Y o u t u b e) and watch a video about it.

Answer:

  (a)  twenty-eight ninths, square root of nineteen, cube root of eighty-eight

Step-by-step explanation:

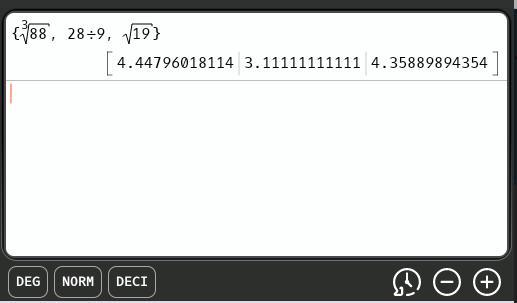
When ordering a list of numbers by hand, it is convenient to convert them to the same form. Decimal equivalents are easily found using a calculator.

The attachment shows the ordering, least to greatest, to be ...

  \(\dfrac{28}{9}.\ \sqrt{19},\ \sqrt[3]{88}\)

__

Additional comment

We know that √19 > √16 = 4, and ∛88 > ∛64 = 4, so the fraction 28/9 will be the smallest. That leaves us to compare √19 and ∛88, both of which are near the same value between 4 and 5.

One way to do the comparison is to convert these to values that need to have the same root:

  √19 = 19^(1/2) = 19^(3/6) = sixthroot(19³)

  ∛88 = 88^(1/3) = 88^(2/6) = sixthroot(88²)

The roots will have the same ordering as 19³ and 88².

Of course, these values can be found easily using a calculator, as can the original roots. By hand, we might compute them as ...

  19³ = (20 -1)³ = 20³ -3(20²) +3(20) -1 = 8000 -1200 +60 -1 = 6859

  88² = (90 -2)² = 90² -2(2)(90) +2² = 8100 -360 +4 = 7744

Then the ordering is ...

  28/9 < 19³ < 88²   ⇒   28/9 < √19 < ∛88

Answer:

the ordering is

28/9 < 19³ < 88²   ⇒   28/9 < √19 < ∛88

Step-by-step explanation:

The correct statement that F: "I agree. The ratios of consecutive x-values are constant, and the y-values are increasing at a constant rate."

To determine whether the function shown in the table is exponential, we need to analyze the relationship between the x-values and y-values.

The table shows x-values that are increasing by a power of 2 (1, 2, 4, 8, 16, 32, 64) and y-values that are increasing by a constant rate of 1 (0, 1, 2, 3, 4, 5, 6).

The constant ratio between consecutive x-values indicates exponential growth or decay.

In this case, the function is growing exponentially because the y-values are increasing at a constant rate.

Based on this information, we can conclude that the function is exponential.

Therefore, we agree with statement F: "I agree. The ratios of consecutive x-values are constant, and the y-values are increasing at a constant rate."

The other statements are incorrect because they do not accurately describe the relationship between the x-values and y-values in an exponential function.

Learn more about exponential function here:

brainly.com/question/11487261

#SPJ1

Ending Inventory Cost and Cost of Goods Sold using different inventory methods:

FIFO Method:

Ending Inventory Cost: $11,920

Cost of Goods Sold: $15,068

LIFO Method:

Ending Inventory Cost: $11,996

Cost of Goods Sold: $15,123

Weighted Average Cost Method:

Ending Inventory Cost: $11,974

Cost of Goods Sold: $15,087

Using the FIFO (First-In, First-Out) method, the cost of the ending inventory is determined by assuming that the oldest units (those acquired first) are sold last. In this case, the cost of the ending inventory is calculated by taking the cost of the most recent purchases (70 units at $142 per unit) plus the cost of the remaining 10 units from the March 10 purchase.

This totals to $11,920. The cost of goods sold is calculated by taking the cost of the units sold (50 units from the Jan. 1 inventory at $124 per unit, 60 units from the March 10 purchase at $132 per unit, and 20 units from the August 30 purchase at $138 per unit), which totals to $15,068.

Using the LIFO (Last-In, First-Out) method, the cost of the ending inventory is determined by assuming that the most recent units (those acquired last) are sold first. In this case, the cost of the ending inventory is calculated by taking the cost of the remaining 10 units from the December 12 purchase, which amounts to $1,420, plus the cost of the 70 units from the August 30 purchase, which amounts to $10,576.

This totals to $11,996. The cost of goods sold is calculated by taking the cost of the units sold (50 units from the Jan. 1 inventory, 60 units from the March 10 purchase, and 20 units from the August 30 purchase), which totals to $15,123.

Using the Weighted Average Cost method, the cost of the ending inventory is determined by calculating the weighted average cost per unit based on all the purchases. In this case, the total cost of all the purchases is $46,360, and the total number of units is 200.

Therefore, the weighted average cost per unit is $231.80. Multiplying this by the 80 units in the physical inventory at December 31 gives a total cost of $11,974 for the ending inventory. The cost of goods sold is calculated by taking the cost of the units sold (50 units from the Jan. 1 inventory, 60 units from the March 10 purchase, and 20 units from the August 30 purchase), which totals to $15,087.

for such more questions on Cost

https://brainly.com/question/2292799

#SPJ8

Answer:

1)

7+9-15 = add 7 and 9, then subtract 15

2)

15-(7+9) = The sum of 7 and 9 subtracted from 15

3)

15-(7+9) =  subtract 7 from 15, then add 9

Step-by-step explanation:

Learn BODMAS. The order of how to do equations. A simple tutorial on yt should be sufficient

Answer:

5 13 and 10

blue cheese

The equation of a line that passes through points (2,5) and (4,3) is

y = -x+7.

Finding the equation of a line:

First, we need to find out the slope for the given points.

(X1,Y1) = (2,5)

(X2,Y2) = (4,3)

formula for slope(m) = \(\frac{Y2 - Y1}{X2 - X1}\)

substitute the points in the above formula

\(\frac{3 - 5}{4 - 2}\) = \(\frac{-2}{2}\)

\(\frac{-2}{2}\) = -1

slope for the given points(m) = -1.

m = -1

The equation of a line is y-y1 = m(x-x1), where x and y are variables.

substituting the values in the above equation then :

y-5 = -1(x-2)

y-5 = -x+2

y+x = 2+5

x+y = 7

y = -x+7

Therefore, the equation of the line passing through the points (2,5) and (4,3) is y = -x+7

To solve more problems based on the linear equations:

https://brainly.com/question/9753782

The slope of a line

Given two points through which a line passes A(x1,y1), B(x2,y2), the slope of the line can be calculated with the formula:

We are given the point A(-4,-8) and the (incomplete) point B(?,1). Knowing the slope is m=2, we can calculate the missing value at point B. Let's call it x: B(x,1).

Substituting all the values in the formula of the slope, we get:

Operating:

Solving for x:

The missing value is 1/2, thus point B is B( 1/2 , 1 )

Step-by-step explanation:

(x-3)(x^2+2x+1)

=x^3-3x^2+2x^2-6x+x-3

=x^3+2x^2-3x^2-6x+x-3

=x^3-x^2-5x-3

___________

Answer:

First write them in positive exponent form

(16/81)¾ × [ (9/25)^3/2 ÷ (2/5)³ ]

(2⁴×¾)/ (3⁴×¾) × [ (3² × ^3/2) / (5² ×^3/2) ÷ 2³/5³)

Simplify the terms

2³/3³ × ( 3³ / 5³ ÷ 2³/5³)

Solve the terms in the bracket

2³/3³ × (3³/5³×5³/2³)

You will get

2³/3³ × 3³/2³ = 1

They will cancel each other so the answer will be 1

Hope this helps.

Answer:

3.5

Step-by-step explanation:

because 7÷4 is 3.5 because seven division of 4 is three point five

Answer:

\(t=\frac{25.5-26}{\frac{1}{\sqrt{8}}}=-1.414\)    

The degrees of freedom are given by:

\(df=n-1=8-1=7\)  

The p value for this case is given by:

\(p_v =P(t_{(7)}<-1.414)=0.100\)  

Since the p value is higher than the significance level of 0.06 we have enough evidence to FAIL to reject the null hypothesis and we can conclude that the true mean is not significantly less than 25.5 and then the claim makes sense

Step-by-step explanation:

Information given

\(\bar X=25.5\) represent the sample mean

\(s=1\) represent the sample standard deviation

\(n=8\) sample size  

\(\mu_o =26\) represent the value to verify

\(\alpha=0.06\) represent the significance level  

t would represent the statistic (variable of interest)  

\(p_v\) represent the p value

Hypothesis to est

We want to test if the true mean is at least 26 mpg, the system of hypothesis would be:  

Null hypothesis:\(\mu \geq 25.5\)  

Alternative hypothesis:\(\mu < 25.5\)  

The statistic for this case is given by;

\(t=\frac{\bar X-\mu_o}{\frac{s}{\sqrt{n}}}\)  (1)  

Replacing the info given we got:

\(t=\frac{25.5-26}{\frac{1}{\sqrt{8}}}=-1.414\)    

The degrees of freedom are given by:

\(df=n-1=8-1=7\)  

The p value for this case is given by:

\(p_v =P(t_{(7)}<-1.414)=0.100\)  

Since the p value is higher than the significance level of 0.06 we have enough evidence to FAIL to reject the null hypothesis and we can conclude that the true mean is not significantly less than 25.5 and then the claim makes sense

Answer:

y = 2x + 10

Step-by-step explanation:

Hi there!

We are given the points (-7, -4) and (-6, -2) and we want to write the equation of the line that passes through these points in slope-intercept form

Slope-intercept form is given as y=mx+b, where m is the slope and b is the y intercept

First, we need to find the slope (m) of the line

The slope can be calculated from 2 points using the formula \(\frac{y_2-y_1}{x_2-x_1}\), where \((x_1, y_1)\) and \((x_2, y_2)\) are points

We have everything we need to find the slope, but let's label the values of the points to avoid any confusion & and mistakes

\(x_1= -7\\y_1=-4\\x_2=-6\\y_2=-2\)

Substitute these values into the formula (note: remember that the formula has subtraction in it!)

m=\(\frac{y_2-y_1}{x_2-x_1}\)

m=\(\frac{-2--4}{-6--7}\)

Simplify

m=\(\frac{-2+4}{-6+7}\)

Add the numbers

m=\(\frac{2}{1}\)

Divide

m=2

The slope of the line is 2

We can substitute that in:

y = 2x + b

Now we need to find b

As the equation passes through both  (-7,-4) and (-6,-2), we can use either point to help solve for b

Taking (-6, -2) for example:

Substitute -6 as x and -2 as y into the equation.

-2 = 2(-6) + b

Multiply

-2 = -12 + b

Add 12 to both sides

-2 = -12 + b

+12  +12

___________

10 = b

Substitute 10 as b.

y = 2x + 10

Hope this helps!

Topic: Finding the equation of a line

See more on this topic here: https://brainly.com/question/27319082

Answer:

Step-by-step explanation:

(-4*5 - 1) + (-4)

(-20 - 1) - 4

-21 - 4

-25

Answer:

C

Step-by-step explanation:

It says he walked 2(3/4) miles in 2 hours, and it wants to know how far he walked in 1 mile, which would be that number divided by 2.

2(3/4) is the same as 2.75

2.75/2=11/8

which is equivalent to 1(3/8) miles

Answer:

1 3/8

Step-by-step explanation:

Double the denominator and numerator to make the numerator even, then divide the numerator by 2 while not changing the denominator any further. This gives you 1 and 3 eighths. Half of 2 is one, so you combine these to get 1 & 3/8

The decimal equivalent of the largest Absolute value, 987654321, is 987,654,321.  the largest absolute value is 987,654,321 and the smallest absolute value is 123,456,789.

The largest and smallest absolute values using the digits 1 to 9, we need to arrange them in a way that maximizes or minimizes the resulting number. Let's consider the boxes as placeholders for the digits.

To determine the largest absolute value:

We place the digit 9 in the leftmost box, as it is the largest digit among 1 to 9. Then we arrange the remaining digits, 8, 7, 6, 5, 4, 3, 2, and 1, from largest to smallest in the remaining boxes. This gives us the number 987654321, which is the largest possible number using the given digits. Therefore, the largest absolute value is 987654321.

To determine the smallest absolute value:

We place the digit 1 in the leftmost box, as it is the smallest digit among 1 to 9. Then we arrange the remaining digits, 2, 3, 4, 5, 6, 7, 8, and 9, from smallest to largest in the remaining boxes. This gives us the number 123456789, which is the smallest possible number using the given digits. Therefore, the smallest absolute value is 123456789.

To find the decimal equivalent of these numbers, we simply read the digits from left to right. The decimal equivalent of the largest absolute value, 987654321, is 987,654,321. The decimal equivalent of the smallest absolute value, 123456789, is 123,456,789.

Thus, the largest absolute value is 987,654,321 and the smallest absolute value is 123,456,789.

To know more about  Absolute value.

https://brainly.com/question/24368848

#SPJ8

Answer:

17

Step-by-step explanation:

2a+30 = 4a-4

+4 +4

2a+34 = 4a

-2a -2a

34 = 2a

÷2 ÷2

a=17

Hope this helps! :)

Answer:

A = 17

Step-by-step explanation:

Opposite angles are congruent in a parallelogram

Hence 2a + 30 = 4a - 4

( Note that we've just created an equation that we can use to solve for a)

We now solve for a

2a + 30 = 4a - 4

Add 4 to both sides

2a + 34 = 4a

Subtract 2a from both sides

34 = 2a

Divide both sides by 2

a = 17

Answer:

  XY = 11.25

Step-by-step explanation:

Corresponding sides of similar triangles are proportional.

  XY/5 = 18/8

  XY = 5(9/4) = 45/4

  XY = 11.25

Answer:

no solutions

Step-by-step explanation:

the equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

equation of blue line is y = x + 2 , in slope- intercept form

with slope m = 1

equation of red line is y = x - 3 , in slope- intercept form

with slope m = 1

• Parallel lines have equal slopes

then the blue and red lines are parallel.

the solution to the system is at the point of intersection of the 2 lines

since the lines are parallel then they do not intersect each other.

thus the system shown has no solution.

Answer:

a I think srry if Rong gzjfzmgxmgzmgxmgzmgzkhdkgdly

Answer:

\(y> 3x + 2\)

Step-by-step explanation:

Hope it is helpful....

The linear inequality that represents the given graph is y > 3x + 2.

The solutions to the graph of the inequalities is given as;

(x, y) = (0, 2)

(x, y) = (-3, -7)

To determine the inequality represented in the graph;

Thus, the linear inequality that represents the given graph is y > 3x + 2.

Learn more about graphs of linear inequality here: https://brainly.com/question/371134

Answer:

how many points will you give?

Step-by-step explanation:

Answer: A) 6x+2

Step-by-step explanation:

I just figured it out

The expression for the given word phrase is

46M + M² + 2 + 1/M²

An expression is a way of writing a statement with more than two variables or numbers with operations such as addition, subtraction, multiplication, and division.

Example: 2 + 3x + 4y = 7 is an expression.

We have,

Number = M

Reciprocal of M = 1/M

Now,

46 x (M + 1/M)²

Step 1:

46M + M² + 2 + 1/M²

Thus,

The expression is 46M + M² + 2 + 1/M²

Learn more about expressions here:

https://brainly.com/question/3118662

#SPJ1

Answer:

2,727 students approximately will have completed the obstacule in 7 years, by 2020

Step-by-step explanation:

Final value = Initial value × (1 + Annual Growth Rate)^No. of years × No. of compounding so

\(1.5%=0.015\) = \(0.015\)

\(F = 2458(1+0.015)^7\)
\(= 2727.998796\) or \(2727\)

Hope this helped and is what you asked for :)

Answer:

Step-by-step explanation:

total interest paid is given as $4,643.46.

total payments = $429.95 x 36 months = $15,478.20

total lease payments = total payments - total interest

total lease payments = $15,478.20 - $4,643.46 = $10,834.74

Remaining balance = Total cost of the lease - Total lease payments

$23,495 - $10,834.74 = $12,660.26