A professional gamer is preparing for a tournament. in his game he averaged a score of 534 points, every day, for 5 days. then, for the next 3 days he scored a total of 1827 points. finally in another 4 days he averaged a score of 516 points each day. in 12 days how many points in total did this gamer get
Answers
In 12 days a professional gamer got 6561 points
We know that average is ratio of the sum of all observations and the number of total observations.
For given question,
A professional gamer averaged a score of 534 points, every day, for 5 days.
⇒ 534 = (total score of 5 days) / 5
⇒ total score of 5 days = 534 × 5
⇒ total score points of 5 days = 2670 points
Then, for the next 3 days he scored a total of 1827 points.
So, the total points of 8 days would be,
total score points of 5 days + total score points of 3 days
⇒ 2670 points + 1827 points = 4497 points.
In another 4 days he averaged a score of 516 points each day.
⇒ 516 = (total score of 4 days) / 4
⇒ total score of 4 days = 516 × 4
⇒ total score points of 4 days = 2064 points
So, the total number of points he did in 12 days:
total score points of 5 days + total score points of 3 days + total score points of 4 days
= 2670 points + 1827 points + 2064 points
= 6561 points
Therefore, in 12 days a professional gamer got 6561 points
Learn more about the average here:
https://brainly.com/question/2906096
#SPJ4
Related Questions
PLEASEEE HELPPP
Find ALL missing angles.
will give brainly
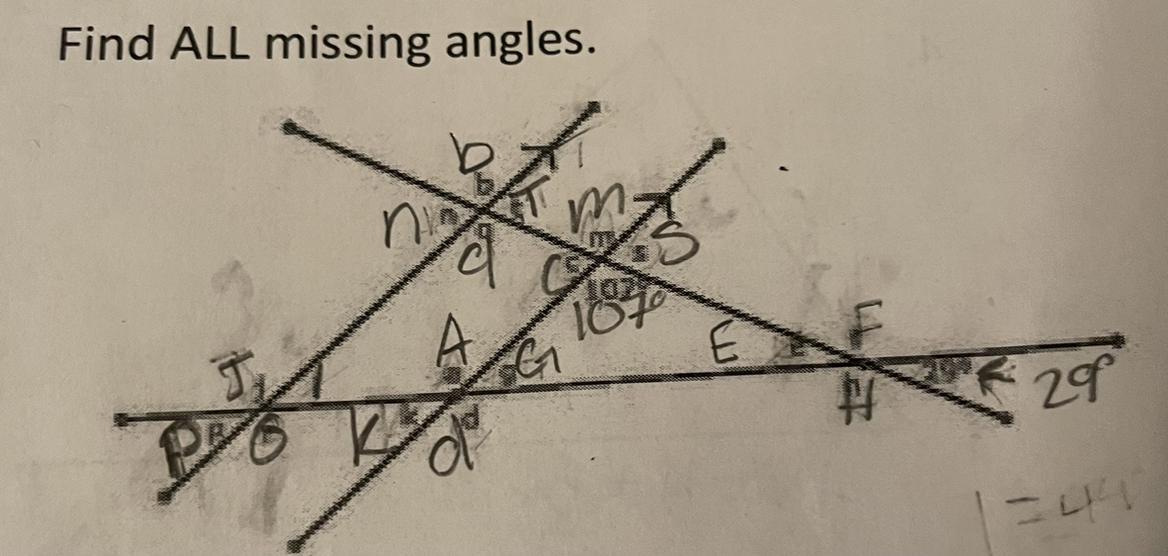
Answers
Step-by-step explanation:
E=29
G = 180-29-107= 44
F = 180-29-29 = 122
H = 180-29-29 = 122
S = 180-107 = 73
M = 107
C = 73
D = 107
T = 73
B = 107
N = 73
K = 44
A = 360-44-44-107 = 165
O = 180-44 = 136
P = 44
J= 136
The p-value of a test of significance is calculated assuming:
a. a significance level of 0.05.
b. the alternative hypothesis is true.
c. the null hypothesis is true.
d. nothing; we make no assumptions about which hypothesis is true in order to avoid bias.
Answers
The p-value of a test of significance is calculated assuming that the null hypothesis is true. Option c. the null hypothesis is true is the correct choice for the assumption made in calculating the p-value.
The p-value represents the probability of obtaining the observed test statistic or a more extreme value, assuming that the null hypothesis is true. It provides evidence against the null hypothesis and helps determine the level of statistical significance. Therefore, option c. the null hypothesis is true is the correct choice when considering the assumptions made in calculating the p-value.
In hypothesis testing, the p-value is a crucial measure that indicates the strength of evidence against the null hypothesis. It represents the probability of observing the test statistic or a more extreme value, assuming that the null hypothesis is true. The p-value allows us to determine the level of statistical significance and decide whether to reject or fail to reject the null hypothesis.
By assuming the null hypothesis is true, we calculate the p-value based on the observed data and the test statistic. The p-value is then compared to a predetermined significance level (commonly set at 0.05) to make a decision regarding the null hypothesis. Option a. a significance level of 0.05 refers to the predetermined threshold at which we decide to reject or fail to reject the null hypothesis, but it is not directly related to the assumption made when calculating the p-value.
Option b. the alternative hypothesis being true is the opposite scenario to the null hypothesis, and it is not the assumption made when calculating the p-value. Option d. making no assumptions about which hypothesis is true would result in a lack of basis for the p-value calculation and would hinder the interpretation of the test's significance. Therefore, option c. the null hypothesis is true is the correct choice for the assumption made in calculating the p-value.
Learn more about probability here: brainly.com/question/31828911
#SPJ11
Please I need help ASSAAAPPP answering this question and if so can you show work PLEASE I’m dEspRate

Answers
The equation needed to calculate the compound interest is \(A = P(1 +\frac{r}{n} )^{nt}\)
The value of the account after ten years is $9347.62 .
If the account is left alone for 20 years, the amount of interest earned is $6942.76
How to calculate compound interest?The compound interest formula is represented as follows;
\(A = P(1 +\frac{r}{n} )^{nt}\)
where
A = amountP = principalr = raten = compounded months, years etc.t = time in yearsTherefore,
where
r = 3.7% = 3.7 / 100 = 0.037
n = 1
t = 10
P = $6500
Hence,
\(A = 6500(1+\frac{0.037}{1} )^{1(10)}\)
\(A = 6500(1.037)^{10}\)
\(A = 6500(1.43809495884)\)
A = 9347.61723247
A = $9347.62
The value of the account after ten years is $9347.62
Interest = 9347.62 - 6500 = 2847.62 dollars
When it is 20 years.
r = 3.7% = 3.7 / 100 = 0.037
n = 1
t = 20
P = $6500
Hence,
\(A = 6500(1+\frac{0.037}{1} )^{1(20)}\)
\(A = 6500(2.06811711064)\)
A = 13442.7612192
A = $13442.76
Interest = 13442.76 - 6500 = 6942.76 dollars
learn more on compound interest here: https://brainly.com/question/14295570
Three of the thirty computers are out of service. What percent of the computers are working?
Answers
Answer:
90% percent of the computers are working.
Step-by-step explanation:
3/30 of the computers don't work and we can simplify this
1/10 or 10% Subtract 10% from 100%
90% are working computers.
Please hwlp me on this one ita urgent.

Answers
pls help with you actually truly know this

Answers
Answer:
x= 72
Step-by-step explanation:
- move 9 to the right.
- when a number moves to the other side, their sign changes.
- in this case, 9 multiplies by 8.
- thus 9 x 8 equals to 72.
Answer:
x=0
Step-by-step explanation:
1.Subtract 8x from both sides
2.Simplify the expression
3.Divide both sides by the same factor
4.Cancel terms that are in both the numerator and denominator
Answer: x=0
-3x+7x=24+5x-4 what is this
Answers
Answer:
-20
Step-by-step explanation:
solve x
4x=24-4+5x
-20=x
Answer:
x = -20
Step-by-step explanation:
-3x + 7x = 24 + 5x - 4
4x = 20 + 5x
0 = 20 + x
x = -20
which situation would best be represented by an inverse variation function? group of answer choices the total cost as a function of the number of items purchased the distance travelled as a function of speed the area of a circle as a function of the radius the time it takes to finish a race as a function of the runner's speed
Answers
The situation that would best be represented by an inverse variation function is (c) The area of a circle as a function of the radius.
An inverse variation function is a mathematical relationship where one variable increases as the other variable decreases, and vice versa. It can be represented by an equation of the form y = k/x, where k is a constant.
Out of the options provided, the situation that would best be represented by an inverse variation function is
c) The area of a circle as a function of the radius.
This is because the area of a circle is given by the formula A = πr^2, where r is the radius. As the radius increases, the area of the circle also increases, but not in a linear way. Instead, the area increases at a decreasing rate. This is an example of inverse variation, where the area (y) increases as the radius (x) decreases, and vice versa. The constant k in this case is π.
Option a) Total cost as a function of the number of items purchased, option b) Distance travelled as a function of speed, and option d) Time it takes to finish a race as a function of the runner's speed, do not represent inverse variation functions.
Therefore, the correct option is (c) The area of a circle as a function of the radius.
Learn more about inverse variation function here
brainly.com/question/29800645
#SPJ4
Which statement explains how the lines x − y = 2 and y = x 1 are related?.
Answers
The lines x - y = 2 and y = x - 1 are related as they are equations of two different lines that intersect at a single point. This is not a valid equation, indicating that the lines are parallel and do not intersect.
The equation x - y = 2 can be rewritten as y = x - 2, which represents a line with a slope of 1 and a y-intercept of -2. On the other hand, the equation y = x - 1 represents a line with the same slope of 1 but a y-intercept of -1.
When we compare the two equations, we can see that they have the same slope, indicating that the lines are not parallel. The lines intersect at a point where their y-coordinates are equal. To find the point of intersection, we can set the two equations equal to each other:
x - 2 = x - 1
By canceling out the x terms, we find:
-2 = -1
This is not a valid equation, indicating that the lines are parallel and do not intersect. Therefore, the two lines x - y = 2 and y = x - 1 are actually parallel lines and do not have a common point of intersection.
Learn more about y-intercept here:
https://brainly.com/question/14180189
#SPJ11
if p(a) = 0.38, p(b) = 0.83, and p(a ∩ b) = 0.57; then p(a ∪ b) =
Answers
The value of the union of sets A and B is, P(A ∪ B) is 0.64.
The union of two sets means the total elements in both the sets combined.
Given: sets P(A) = 0.38, P(B) = 0.83, and intersection P(A ∩ B) = 0.57
We need to find the union of P(A ∪ B).
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
Let us substitute the given values in the formula.
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
=0.38+0.83-0.57
=1.21-0.57
=0.64
Therefore, the value of union of sets P(A ∪ B) is 0.64.
#SPJ11
Let us know more about sets : https://brainly.com/question/30705181.
The Nielsen Company surveyed 371 owners of Android phones and found that 200
of them planned to get another Android as their next phone. What is the lower
bound for the 95% confidence interval for the proportion of Android users who plan
to get another Android?
Answers
The lower bound for the 95% confidence interval for the proportion of Android users who plan to get another Android phone is 0.463 .
It can be evaluated applying the formula
Lower Bound = Sample Proportion - Z-Score × Standard Error
Here
Sample Proportion
= 200/371 = 0.539
Z-Score = 1.96 (for a 95% confidence interval)
Standard Error = √[(Sample Proportion * (1 - Sample Proportion)) / Sample Size]
= √[(0.539 × (1 - 0.539)) / 371]
= 0.045
Therefore,
Lower Bound = 0.539 - 1.96 × 0.045 = 0.463
A confidence interval is a known as the specified range of values that is prone to contain an unknown population area with a certain degree of confidence.
To learn more about confidence interval
https://brainly.com/question/20309162
#SPJ4
Express the function graphed on the axes below as a piecewise function.104-10-8-6-4-2246810-6

Answers
Step 1
Find the equation of both lines using
\(\frac{y_2-y_1}{x_2-x_1}=\text{ }\frac{y-y_1}{x-x_1}\)Where,
\(\begin{gathered} y_1=-9 \\ y_2=\text{ -2} \\ x_1=\text{ -6} \\ x_2=1 \end{gathered}\)Hence,
\(\frac{-2-(-9)}{1-(-6)}=\frac{y-(-9)}{x-(-6)}\)\(\begin{gathered} \frac{7}{7}=\frac{y+9}{x+6} \\ y+9\text{ = x+6} \\ y\text{ = x+6-9} \\ y\text{ = x-}3 \end{gathered}\)For the second line we will have
\(\begin{gathered} \frac{-4-(-8)}{1-5}=\text{ }\frac{y-(-8)_{}}{x-5} \\ \frac{4}{-4}=\frac{y+8}{x-5} \\ -1(x-5)\text{ = y+8} \\ -x+5\text{ = y+8} \\ y\text{ =- x+5-8} \\ y\text{ = -x-3} \end{gathered}\)Step 2
Hence expressed the graphed solution as a piecewise function
\(f(x)=\begin{cases}x-3,-6\leq x<1 \\ \square \\ -x-3,-1Which points define the solution set of this linear-quadratic system of equations?
A. point A and point B
B. point D and point F
C. point C and point E
D. point B and point D

Answers
Answer:
C. C and E
Step-by-step explanation:
The solutions for a system of equations is the point of intersection of the two graphs of those equations. Here, there are two points of intersection, that is, two points where the graphs cross. The graphs cross at point C and point E.
C and E are the solutions to this system.
let r(x) = f(g(x)) and s(x) = g(f(x)), where f and g are shown in the figure. find r'(1) and s'(4).
Answers
The value of r'(1) and s'(4) is 0 that can be interpreted with the help of the graph that is given in the question.
Derivative in mathematics, the rate of change of a characteristic with recognize to a variable. Derivatives are essential to the answer of troubles in calculus and differential equations. The essence of calculus is the by-product. The by-product is the immediately price of extrade of a characteristic with recognize to certainly considered one among its variables. This is equal to locating the slope of the tangent line to the characteristic at a point
\(r(x) = f(g(x))\)therefore the derivative of r is given by \(r'(x) = f'g(x)\times g'(x)\)
\(r'(1) = f'(g(1))\times g'(1)\) from the graphs
r'(1) = f'4 \times g'1 = (5/4) \times(0) = 0
Similarly s'(1) = g'(f(1))\times f'(1) from the graphs
f(1)=1.5, f'(1)
=\dfrac{ (3-0)}{(0-2)}
= -3/2 , g'(3/2) = 0
s'(4) = g'(3/2) \times f'(4) = 0(-1.5) = 0
To learn more about derivative check the link below:
https://brainly.com/question/23819325
#SPJ4
Complete question:
let r(x) = f(g(x)) and s(x) = g(f(x)), where f and g are shown in the figure. find r'(1) and s'(4).

i need this answered asap

Answers
Answer :
\(p = 169\)

435 divided by 13,050
Answers
13,050/435 = 30
A solid object has the right triangle with vertices (0, 0), (3, 0), and (0, 4) as its base.
a) Any cross section of the solid, taken parallel to the y-axis and perpendicular to the x-axis, is a square. Find the volume of the solid.
b) Any cross section of the solid, taken parallel to the y-axis and perpendicular to the x -axis, is a smi-circle. Find the volume of the solid.
Answers
a. The volume of the solid is 24 cubic units.
b. The volume of the solid is 4π cubic units.
How to calculate tie valuea. Volume = Area of Base * Height
The base is a right triangle with base length of 3 units and height of 4 units. The area of the base can be calculated as:
Area of Base = (1/2) * base * height
= (1/2) * 3 * 4
= 6 square units
The height of the solid is 4 units.
Volume = Area of Base * Height
= 6 * 4
= 24 cubic units
b) Any cross section of the solid, taken parallel to the y-axis and perpendicular to the x-axis, is a semicircle.
Volume = (1/2) * π * radius² × height
Volume = (1/2) * (1/2) * π * 2² * 4
= (1/4) * π * 4 * 4
= π * 4
Therefore, the volume of the solid is 4π cubic units.
Learn more about volume on
https://brainly.com/question/27710307
#SPJ1
what is the result of the following code snippet? double bottles; double bottlevolume = bottles * 2; system.out.println(bottlevolume);
Answers
The output obtained after executing the java code snippet,
double bottles;
double bottleVolume = bottles * 2;
System.out.printIn(bottleVolume);
will throw an error that bottle variable might not have been initialized.
As per the question statement, we are provided with a java code snippet, which goes as:
double bottles;
double bottleVolume = bottles * 2;
System.out.printIn(bottleVolume);
We are required to determine the output, that we will obtain on executing the above mentioned code.
That is, on executing the code
double bottles;
double bottleVolume = bottles * 2;
System.out.printIn(bottleVolume);
We will obtain an error that bottle variable might not have been initialized because we are using the variable bottle without initializing.
Java: Java is a general-purpose, class-based, object-oriented programming language designed for having lesser implementation dependencies, where all programs are made of entities representing concepts or physical things known as “objects”Output: Output is the result of any action.To learn more about Java Code snippets and their Outputs, click on the link below
brainly.com/question/28400793
#SPJ4
Which set of ordered pairs does not represent a function? O {(9,3), (2,-2), (2,6), (-5,2)} O {(-7,-5), (2, -7), (-4,7),(7,-5)} O{(-1, -8), (0, -2), (9,6), (-3, -2)} O {(1,0),(-1,9), (3, 2), (-7, -2)} 2 9 Submit Answer

Answers
Answer:
Step-by-step explanation:

2000(x - 3) = 6000 but distributing it
Answers
Answer:
x=6
Step-by-step explanation:
2000(x-3)=6000
divide both sides by 2000 to cancel it
x-3=3
add (+3) to both sides to cancel the -3
x=6
Use Parseval's identity to find the sum of the following series: a) ∑
n=1
[infinity]
n
2
1
using the Fourier sine series for f(x)=x on 0≤x≤π. b) ∑
k=1
[infinity]
(2k+1)
4
1
using the Fourier cosine series for f(x)=x on 0≤x≤π.
Answers
The sum of the given Fourier sine series is equal to (1/π) * ∫[0 to π] |f(x)|² dx, where f(x) = x.
to find the sum of the given series using Parseval's identity, we need to follow these steps:
a) For the series ∑[n=1 to ∞] n²/1², we will use the Fourier sine series for f(x)
= x on 0≤x≤π.
Step 1: Express f(x) as an odd function by extending it to the interval [-π, π] with f(-x) = -f(x).
Since f(x) = x is already an odd function, we don't need to extend it.
Step 2: Calculate the Fourier coefficients of the odd extension.
The Fourier sine series coefficients for an odd function are given by:
b_n = (2/π) * ∫[0 to π] f(x) * sin(n*x) dx
For f(x) = x, the Fourier sine series coefficients are:
b_n = (2/π) * ∫[0 to π] x * sin(n*x) dx
Step 3: Calculate the sum of the series using Parseval's identity.
Parseval's identity states that for a function f(x) with its Fourier series coefficients b_n, the sum of the series can be found using the formula:
∑[n=1 to ∞] |b_n|²= (1/π) * ∫[0 to π] |f(x)|² dx
In our case, we have:
∑[n=1 to ∞] n²/1² = ∑[n=1 to ∞] |b_n|²
Therefore, the sum of the series is equal to:
(1/π) * ∫[0 to π] |f(x)|² dx
= (1/π) * ∫[0 to π] x² dx
b) For the series ∑[k=1 to ∞] (2k+1)⁴/1², we will use the Fourier cosine series for f(x)
= x on 0≤x≤π.
Step 1: Express f(x) as an even function by extending it to the interval [-π, π] with f(-x) = f(x).
Since f(x) = x is already an even function, we don't need to extend it.
Step 2: Calculate the Fourier coefficients of the even extension.
The Fourier cosine series coefficients for an even function are given by:
a_0 = (1/π) * ∫[0 to π] f(x) dx
a_n = (2/π) * ∫[0 to π] f(x) * cos(n*x) dx
For f(x) = x, the Fourier cosine series coefficients are:
a_0 = (1/π) * ∫[0 to π] x dx
a_n = (2/π) * ∫[0 to π] x * cos(n*x) dx
Step 3: Calculate the sum of the series using Parseval's identity.
Parseval's identity states that for a function f(x) with its Fourier series coefficients a_n, the sum of the series can be found using the formula:
∑[n=0 to∞] |a_n|²= (1/π) * ∫[0 to π] |f(x)|² dx
In our case, we have:
∑[k=1 to ∞] (2k+1)⁴/1² = ∑[n=0 to ∞] |a_n|²
Therefore, the sum of the series is equal to:
(1/π) * ∫[0 to π] |f(x)|² dx = (1/π) * ∫[0 to π] x² dx
Learn more about Fourier sine series with the given link,
https://brainly.com/question/33181075
#SPJ11
I will give brainliest answer to these questions

Answers
Answer:
THATS MADDDD CAPPPP U NEED 25 POINTS OF THE QUESTION FOR BRAINLIEST
(1 point) using: limx→3f(x)=1 and limx→3g(x)=8, evaluate the limits,
Answers
The limit of the function f(x) as x approaches 3 is 1, and the limit of the function g(x) as x approaches 3 is 8.
Given that \(\(\lim_{{x \to 3}} f(x) = 1\)\) and \(\(\lim_{{x \to 3}} g(x) = 8\)\), we can evaluate the limits as follows:
\(\[\lim_{{x \to 3}} (f(x) + g(x)) = \lim_{{x \to 3}} f(x) + \lim_{{x \to 3}} g(x) = 1 + 8 = 9.\]\)
This is known as the limit addition property, which states that the limit of the sum of two functions is equal to the sum of their individual limits if both limits exist.
Similarly, we can evaluate the limit of the product of f(x) and g(x):
\(\[\lim_{{x \to 3}} (f(x) \cdot g(x)) = \lim_{{x \to 3}} f(x) \cdot \lim_{{x \to 3}} g(x) = 1 \cdot 8 = 8.\]\)
This is known as the limit multiplication property, which states that the limit of the product of two functions is equal to the product of their individual limits if both limits exist.
In conclusion, the limit of the sum of f(x) and g(x) as x approaches 3 is 9, and the limit of the product of f(x) and g(x) as x approaches 3 is 8.
To learn more about function refer:
https://brainly.com/question/25638609
#SPJ11
If the volume of a cube is 27in to the power of 3what is the length of one side of the cube?
Answers
Answer:
3
Step-by-step explanation:
because 3 square 3 gives 27
WILL GIVE BRAILIEST PLZZZZ HELP MEEEEEE
A teacher surveyed her class after they had taken a vocabulary test. Eighteen of the students claimed they had studied at least one hour for the test. The remaining twelve students admitted that they had not studied for the test at all. The test results (expressed as a percent) for the two groups are shown below.
Studied: 88, 100, 94, 79, 92, 100, 95, 83, 89, 99, 100, 91, 89, 95, 100, 93, 96, 84
Did Not Study: 82, 72, 45, 91, 58, 83, 65, 87, 90, 77, 73, 89
Which of the following statements are true?
There is no mode of the group that studied.
In general, those students that studied scored much higher than those students that did not study.
The mean of the group that studied is over 15 percentage points higher than the mean of the group that did not study.
The median of the group that studied is over 95.
The median of the group that did not study is less than 80.
Answers
Answer:
In general, those students that studied scored much higher than those students that did not study.
Step-by-step explanation:
Hope this helps.
The median of the group that did not study is less than 80.
also
In general, those students that studied scored much higher than those students that did not study.
Suppose 8x+16 ice cream cones were sold on Saturday and 7x-9 were sold on Sunday. What is the total number of ice cream cones sold?
Answers
Answer:
8x+16
7x-9
_____
15x+7
Step-by-step explanation:
Add or subtract like terms
Answer:
15x+7
No step I did it
Write 47 5 as a mixed number.
Answers
The fraction, \(4\frac{7}{5}\) as a mixed number can be written as, 5 whole and \(\frac{2}{5}\).
What is a fraction?A fraction is written in the form of p/q, where q ≠ 0.
Fractions are of two types they are proper fractions in which the numerator is smaller than the denominator and improper fractions where the numerator is greater than the denominator.
A mixed number is a representation of both a whole number and a legal fraction. In most cases, it denotes a number that falls between any two whole numbers.
Given, A fraction \(4\frac{7}{5}\),
Now, \(4\frac{7}{5}\) = \(4 + 1\frac{2}{5}\).
= \(5 \frac{2}{5}\).
This can be written as a whole number 5 and a proper fraction \(\frac{2}{5}\).
Q. Write \(4\frac{7}{5}\) as a mixed number.
learn more about fractions here :
https://brainly.com/question/10354322
#SPJ1
There are 18 students attending band camp,4 girls and 14 boys. wht is the ratio of girls to boys at band camp?
A. 7:2
B.2:7
C. 8:3
Answers
Answer:
B
Step-by-step explanation:
4÷2=2
14÷2=7
making it a equal ratio
27.6 inches of rain fell over a 100 day period. What was the average amount of rain that fell per day? Enter a numerical answer only.
Answers
Answer:
Step-by-step explanation:
Hey ! I beleive this is the answer: 27.5/100=.275
Becky's statistics teacher was teaching the class how to perform the z-test for a proportion. Becky was bored because she had already mastered the test, so she decided to see if the coin she had in her pocket would come up heads or tails in a truly random fashion when flipped. She discretely flipped the coin 30 times and got heads 18 times.
Becky conducts a one-proportion hypothesis test at the 5% significance level, to test whether the true proportion of heads is different from 50%.
Which answer choice shows the correct null and alternative hypotheses for this test?
Select the correct answer below:
H0:p=0.6; Ha:p>0.6, which is a right-tailed test.
H0:p=0.5; Ha:p<0.5, which is a left-tailed test.
H0:p=0.6; Ha:p≠0.6, which is a two-tailed test.
H0:p=0.5; Ha:p≠0.5, which is a two-tailed test.
Answers
The correct null and alternative hypotheses for Becky's one-proportion hypothesis test are H0: p = 0.5 and Ha: p ≠ 0.5 (The true proportion of heads is different from 50%).
This represents a two-tailed test because the alternative hypothesis (Ha) includes the "≠" symbol, indicating that the true proportion of heads could be either greater than or less than 50%.
In this case, Becky conducted a coin flip experiment, where she flipped the coin 30 times and obtained 18 heads. By comparing the observed proportion (18/30 = 0.6) to the hypothesized proportion of 0.5 (50%), she wants to determine if there is evidence to suggest that the coin is biased and not coming up heads or tails in a truly random fashion.
To perform the hypothesis test, she will calculate the test statistic (Z) and compare it to the critical value(s) corresponding to her chosen significance level of 5%. If the test statistic falls in the rejection region, she would reject the null hypothesis and conclude that there is evidence to suggest that the true proportion of heads is different from 50%.
Therefore, by using the correct null and alternative hypotheses, Becky can proceed with her hypothesis test accurately and draw valid conclusions regarding the randomness of her coin flips.
To learn more about hypothesis test from the given link
https://brainly.com/question/29576929
#SPJ4