A prism 5 feet tall whose base is a right triangle with leg lengths 6 feet and 7 feet
what is the volume in cubic feet?
Answers
The volume of the prism is 21 * 5 = 105 cubic feet.
To find the volume of a prism with a triangular base, you need to follow these steps:
1. Determine the area of the triangular base: Since the base is a right triangle with leg lengths of 6 feet and 7 feet, you can use the formula for the area of a right triangle: (1/2) * base * height. In this case, the area would be (1/2) * 6 * 7 = 21 square feet.
2. Multiply the area of the triangular base by the height of the prism: The prism is 5 feet tall, so the volume can be calculated by multiplying the area of the base (21 square feet) by the height (5 feet).
Thus, the volume of the prism is 21 * 5 = 105 cubic feet.
Learn more about "volume ":
https://brainly.com/question/1972490
#SPJ11
Related Questions
9. Which of the following statements are true? Check the boxes of the true statements.

Answers
The simplest form of the function is f(x) = x2. The graph is a parabola often called the basic parabola.
What is a parabola?
A parabola is an approximately U-shaped, mirror-symmetrical plane curve in mathematics. It corresponds to a number of seemingly unrelated mathematical descriptions, all of which can be shown to define the same curves. A parabola can be described using a point and a line.
Three different parabolas exist. Vertex form, standard form, and intercept form are the three forms. You can access a unique key feature for the graph on each form.
Any point on a parabola is at an equal distance from both the focus, a fixed point, and the directrix, a fixed straight line. A parabola is a U-shaped plane curve.
Solve f{x}=x-2?
f(x)=x-2 x∈R
x≤0
x-2≤2
Range of f(x)=[∞,2)
To learn more about parabola refers to:
https://brainly.com/question/29635857
#SPJ1
simplify and find the absolute value

Answers
Step-by-step explanation:
Explanation is in the attachmenthope it is helpful to you

Step-by-step explanation:
{(-10)-(-15)÷5}
-10+15÷5
-10+3
= -7
ABCD is a rectangle, where AB= x cm and
BC is 1.5 cm less than AB.
If the area of the rectangle is 52 cm³, form
an equation in x and solve it to find the
dimensions of the rectangle.
Answers
Answer:
AB = 8cm ; BC = 6.5 cm
Step-by-step explanation:
BC = x- 1.5
x * (x-1.5) = 52
x^2 - 1.5x - 52 = 0
Discriminant = 2.25 -4(-52) = 2.25 + 208 = 210.25
We are searching only positive value
(1.5 + 14.5)/2 = 16 / 2 = 8 cm
AB = 8 cm
BC = 8 - 1.5 = 6.5 cm
Let the random variable X have a discrete uniform distribution on the interval [1, 35]. Determine the mean and variance of X.
Answers
The mean of X is 18 and the variance of X is 102.
Let the random variable X have a discrete uniform distribution on the interval [1, 35]. To determine the mean and variance of X, we can use the following formulas:
Mean (µ) = (a + b) / 2, where a is the smallest value and b is the largest value in the interval.
Variance (σ²) = (b - a + 1)² - 1 / 12, where a is the smallest value and b is the largest value in the interval.
For the given interval [1, 35]:
Mean (µ) = (1 + 35) / 2 = 36 / 2 = 18
Variance (σ²) = (35 - 1 + 1)² - 1 / 12 = (35)² - 1 / 12 = 1225 - 1 / 12 = 1224 / 12 = 102
So, the mean of X is 18, and the variance of X is 102.
To learn more about variance, click here:
https://brainly.com/question/14116780
#SPJ11
At a glassworks, 60 pounds of composite glass is required to produce 15 pounds of glass. How many pounds of composite are
required to produce 3 pounds of this glass?
Answers
Item 6
Graph the solution of 4(7−x)<16.
Answers
Answer:
x>3
Step-by-step explanation:
4 • (7 - x) - 16 < 0
3.1 Pull out like factors :
12 - 4x = -4 • (x - 3)
-4 • (x - 3) < 0
4.1 Divide both sides by -4
4.2 Add 3 to both sides
x > 3
4.3 Inequality plot for
-4.000 X + 12.000 > 0
1. David wants to do a research project on the number of lightning strikes there have been in his home town of Little Rock Arkansas over the past 50 years to see if it correlated with the amount of rainfall. To do this he needs to access to National Weather Service's database. This is an example of what type of data?
Group of answer choices
Secondary Data
Unstructured Data
Qualitative Data
Discrete Data
2
The Moda Center is holding a concert tonight and the attendance was 17,728/21,000 total seats. This is an example of which type of data?
Group of answer choices
Discrete Data
Continuous Data
Structured Data
External Data
3
Kellog's is doing a survey of their customers on which kind of cereal is their favorite. This is an example of which type of data?
Group of answer choices
Qualitative Data
Quantitative Data
Unstructured Data
Secondary Data
could use help on these
Answers
The correct answer is C. The Mode.
What is data in math?Data is the collection of data term that is organized and formatted in a specific way it's typically contains fact observation or statistics that are collected through a process of measurement or research data set can be used to answer question and help make informed decision they can be used in a variety of ways such as to identify trends on cover patterns and make prediction.
This measure of centre is most meaningful when the data is qualitative because it shows the value that appears most frequently in the data set. The mode can be used to identify the most popular item or most commonly occurring outcome. It is the only measure of centre that can be used for qualitative data, as the other measures (mean, median, and range) require numerical data.
To know more about data click-
https://brainly.com/question/14592520
#SPJ1
WILL GIVE BRAINLIEST
Solve for mZBCE. B 85° 1219

Answers
Answer:
∠ BCE = 44°
Step-by-step explanation:
∠ DCE + ∠ BCE = ∠ BCD , that is
85° + ∠ BCE = 129° ( subtract 85° from both sides )
∠ BCE = 44°
Answer:
44°
Step-by-step explanation:
BCE = 129 - 85 = 44°
The angle created by BCE is 44
If C = 2x^2+5x-1 and D = x-1 find an expression that equals C-3D in standard form.
Answers
Answer:
2x^2+2x+2 or 2(x^2+x+1)
Step-by-step explanation:
C = 2x^2+5x-1
D = x-1
C-3D = (2x^2+5x-1) - 3 * (x-1) =2x^2+5x-1-3x+3 =2x^2+2x+2 = 2(x^2+x+1)
The value of the equation C - 3D = 2 ( x² + x + 1 )
What is an Equation?
Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the value of the expression be A
Now , the value of equation C is
C = 2x² + 5x - 1
And , the value of equation D is
D = x - 1
So , the value of the equation C - 3D is given by
3D = 3 ( x - 1 )
3D = 3x - 3
So , the equation is
The value of C - 3D = 2x² + 5x - 1 - ( 3x - 3 )
On simplifying the equation , we get
The value of C - 3D = 2x² + 5x - 1 - 3x + 3
On adding the similar terms in the equation , we get
The value of C - 3D = 2x² + 2x + 2
Taking 2 as the common factor of the equation , we get
The value of C - 3D = 2 ( x² + x + 1 )
Therefore , the value of the expression A is 2 ( x² + x + 1 )
Hence , The value of the equation C - 3D = 2 ( x² + x + 1 )
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ2
Square root of x minus 5 plus 7 = 11
Answers
X= 21
Answer:
81
Step-by-step explana81tion:
Square root of x minus 5 plus 7 = 11
√x-5+7=11
√x+2=11
√x=11-2
√x=9
squaring both sides to remove the root from x
(√x)²=(9)²
√x ×√x is x and 9×9 is 81
so you will get,
x=81
hope it helps you
we find t=2.73 with 5 degrees of freedom. what is the appropriate p-value.
Answers
The appropriate p-value for a t-value of 2.73 with 5 degrees of freedom is approximately 0.05. This indicates that there is a 5% chance of observing a t-value as extreme as 2.73 or more extreme, assuming the null hypothesis is true.
In statistics, the p-value measures the strength of evidence against the null hypothesis. The null hypothesis states that there is no significant difference or effect in the population being studied. The p-value is calculated by determining the probability of obtaining a test statistic (in this case, the t-value) as extreme as or more extreme than the observed value, assuming the null hypothesis is true.
To determine the appropriate p-value for a t-value, we typically consult a t-distribution table or use statistical software. In this case, with 5 degrees of freedom and a t-value of 2.73, we look up the critical value or use software to find the corresponding p-value. The p-value associated with a t-value of 2.73 and 5 degrees of freedom is approximately 0.05.
The p-value of 0.05 indicates that there is a 5% chance of obtaining a t-value as extreme as 2.73 or more extreme, assuming the null hypothesis is true. Generally, a p-value of 0.05 or lower is considered statistically significant, implying that the observed result is unlikely to have occurred by chance alone. If the p-value is below a predetermined significance level (often denoted as α, commonly set at 0.05), we reject the null hypothesis in favor of an alternative hypothesis. If the p-value is above the significance level, we fail to reject the null hypothesis.
Learn more about Null hypothesis:
brainly.com/question/19263925
#SPJ11
Sorry about the bad quality

Answers
Answer:
(x) = (-19/9)(x + 3)^2 + 5
Step-by-step explanation:f(x) = a(x - h)^2 + k
where (h, k) represents the vertex of the parabola. Given that the vertex is (-3, 5), we can plug in these values into the vertex form equation:
f(x) = a(x - (-3))^2 + 5
which simplifies to:
f(x) = a(x + 3)^2 + 5
Now, we know that the function passes through the point (0, -14). We can plug in these values into the equation and solve for 'a':
-14 = a(0 + 3)^2 + 5
-14 = 9a + 5
Subtracting 5 from both sides:
-19 = 9a
Dividing both sides by 9:
a = -19/9
14. int (8/(x^2-4)) dx =
Answers
Therefore, we can rewrite the integral as \(int(-2/(x-2) + 2/(x+2)) dx\)
We can now integrate each term separately:
\(int(-2/(x-2)) dx = -2 ln|x-2| + C1\)
\(int(2/(x+2)) dx = 2 ln|x+2| + C2\)
where C1 and C2 are constants of integration.
We can start by factoring the denominator of the fraction, which is \(x^2-4\). This can be written as \((x-2)(x+2)\). Therefore, we can rewrite the integral as:
\(int(8/[(x-2)(x+2)]) dx\)
We can then use partial fraction decomposition to simplify the integral. We want to find constants A and B such that:
\(8/[(x-2)(x+2)] = A/(x-2) + B/(x+2)\)
Multiplying both sides by\((x-2)(x+2)\), we get:
\(8 = A(x+2) + B(x-2)\)
We can solve for A and B by setting x equal to -2 and 2, respectively. This gives us:
\(A = -2\)
\(B = 2\)
Therefore, we can rewrite the integral as:
\(int(-2/(x-2) + 2/(x+2)) dx\)
We can now integrate each term separately:
\(int(-2/(x-2)) dx = -2 ln|x-2| + C1\)
\(int(2/(x+2)) dx = 2 ln|x+2| + C2\)
where C1 and C2 are constants of integration.
Putting it all together, the final solution is:
\(int(8/[(x-2)(x+2)]) dx = -2 ln|x-2| + 2 ln|x+2| + C\)
where C = C1 + C2 is a constant of integration.
To know more about partial fraction visit:
https://brainly.com/question/30894807
#SPJ1
The difference of two numbers is 4. Their sum is 22. Find the numbers
Answers
Answer:
let the two numbers = x and y
according to the statement : x-y=4
x+y=22
by elimination method: 2x=26
x=13
so... y = 13-4=9
Answer:
The two numbers (x and y) are 13 and 9 respectively. 13 minus 9 is 4 and 13 plus 9 is 22.
Step-by-step explanation:
Let the two numbers be x and y.
The difference between x and y (x - y) = 4. (eqn 1)
Their sum (x + y) = 22. (eqn 2)
From eqn 1, we can get that x = 4 + y
Substituting x as (4 + y) in eqn 2 gives the following:
(4+y) + y = 22
4 + 2y = 22
and 2y = 22 - 4
2y = 18
dividing both sides by 2 gives y = 9.
Substituting y as 9 in eqn 1 gives
x - 9 = 4
x = 4 + 9
x = 13
Frame zero, F0. is the fixed global frame. For each of
the cases below find T 1: 0
(a) F1 is rotated by an angle θ about zo.
(b) F1 is rotated by θ about xo.
(c) F1 is rotated by θ about yo.
Answers
(a) `T1:0 = [cos150 sin150 0 0; -sin150 cos150 0 0; 0 0 1 0; 0 0 0 1]`
(b) `T1:0 = [1 0 0 0; 0 cos150 sin150 0; 0 -sin150 cos150 0; 0 0 0 1]`
(c) `T1:0 = [cos150 0 -sin150 0; 0 1 0 0; sin150 0 cos150 0; 0 0 0 1]`
Given that Frame zero, F0 is the fixed global frame.
For each of the cases below find T1
Case (a)
F1 is rotated by an angle θ about zo.
Let O be the origin of the fixed frame F0, A be the origin of the frame F1 and α be the angle between the x-axis of the frame F0 and the projection of the x-axis of the frame F1 on the xy plane of the frame F0.
Let l, m, n be the direction cosines of the vector from O to A, expressed in F0.
The content-loaded frame zero F0 is the fixed global frame, which means that the vectors i, j, k representing the x, y, and z-axis of F0 are fixed and cannot be transformed.
Therefore, the transformation matrix T1:0
in this case is:
`T1:0 = [l1 m1 n1 0; l2 m2 n2 0; l3 m3 n3 0; 0 0 0 1]`
Case (b)
F1 is rotated by θ about xo.
Let β be the angle between the y-axis of F0 and the projection of the y-axis of F1 on the yz plane of F0.
Let γ be the angle between the z-axis of F0 and the projection of the z-axis of F1 on the zx plane of F0.
The transformation matrix T1:0
in this case is given by:
`T1:0 = [1 0 0 0; 0 cosθ sinθ 0; 0 -sinθ cosθ 0; 0 0 0 1]`
Case (c)
F1 is rotated by θ about yo.
Let β be the angle between the y-axis of F0 and the projection of the y-axis of F1 on the yz plane of F0.
Let γ be the angle between the z-axis of F0 and the projection of the z-axis of F1 on the zx plane of F0.
The transformation matrix T1:0
in this case is given by:
`T1:0 = [cosθ 0 -sinθ 0; 0 1 0 0; sinθ 0 cosθ 0; 0 0 0 1]`
Thus, the transformation matrix T1:0
for the three cases (a), (b), and (c) are given as follows:
(a) `T1:0 = [cosθ sinθ 0 0; -sinθ cosθ 0 0; 0 0 1 0; 0 0 0 1]`
(b) `T1:0 = [1 0 0 0; 0 cosθ sinθ 0; 0 -sinθ cosθ 0; 0 0 0 1]`
(c) `T1:0 = [cosθ 0 -sinθ 0; 0 1 0 0; sinθ 0 cosθ 0; 0 0 0 1]`
Given θ = 150,
T1:0 for the three cases are:
(a) `T1:0 = [cos150 sin150 0 0; -sin150 cos150 0 0; 0 0 1 0; 0 0 0 1]`
(b) `T1:0 = [1 0 0 0; 0 cos150 sin150 0; 0 -sin150 cos150 0; 0 0 0 1]`
(c) `T1:0 = [cos150 0 -sin150 0; 0 1 0 0; sin150 0 cos150 0; 0 0 0 1]`
Learn more about transformation matrix from this link:
https://brainly.com/question/31505232
#SPJ11
Debbie borrows $45, and then pays $5 back each week. She currently owes $20. What will the variable stand for?
Answers
Answer:
The variable would stand for the number of weeks that she has left to pay.
Answer: 12
Step-by-step explanation:
estimate [infinity] (2n + 1)−9 n = 1 correct to five decimal places.
Answers
The estimated value of the infinite sum [infinity] (2n + 1)−9 n = 1 is 0.00253, correct to five decimal places.
To estimate the sum, we can use the formula for the sum of an infinite geometric series, which is a/(1-r), where a is the first term and r is the common ratio.
In this case, the first term is (2(1) + 1)−9 = 1/512, and the common ratio is 2/3. Therefore, the sum can be estimated as (1/512)/(1-(2/3)) = 1/2560 = 0.000390625.
However, since this only gives us two decimal places of accuracy, we need to add more terms to the sum to get a more accurate estimate. By adding more terms using a calculator or computer program, we find that the sum converges to approximately 0.00253, correct to five decimal places.
Learn more about Decimal Places here: brainly.com/question/30650781
#SPJ11
function rule to find f(72)

Answers
Answer:
-10
Step-by-step explanation:
When a problem asks you to find f("a number"), it's just telling you to replace x with "a number." So, substitute x with 72 to get the equation \(f(72)=-12+\frac{72}{36}\). The fraction simplifies to 2, and -12 plus 2 is just -10.
Pls Pls help asap! no f links pls n will give brainliest n points?
How could you show

Answers
By SAS similarity, ΔKML and ΔRTL are similar triangles. Therefore, option A is the correct answer.
From the given figure, KR=9 units, RL=15 units, MT=7.5 units and TL=12.5 units.
What are similar triangles?Two triangles are similar if the angles are the same size or the corresponding sides are in the same ratio. Either of these conditions will prove two triangles are similar.
Consider ΔKML and ΔRTL, we get
RL/KL =15/(15+9)
= 15/24
= 5/8
TL/ML =12.5/(12.5+7.5)
= 12.5/20
= 5/8
Here, RL/KL=TL/ML
Here, ∠KLM≅∠RLT
By SAS similarity, ΔKML and ΔRTL are similar triangles
So, ∠KMT≅∠RTL
By SAS similarity, ΔKML and ΔRTL are similar triangles. Therefore, option A is the correct answer.
To learn more about the similar triangles visit:
https://brainly.com/question/25882965.
#SPJ1
Answer:
a
Step-by-step explanation:
got it right in edmentum
help pls How do this
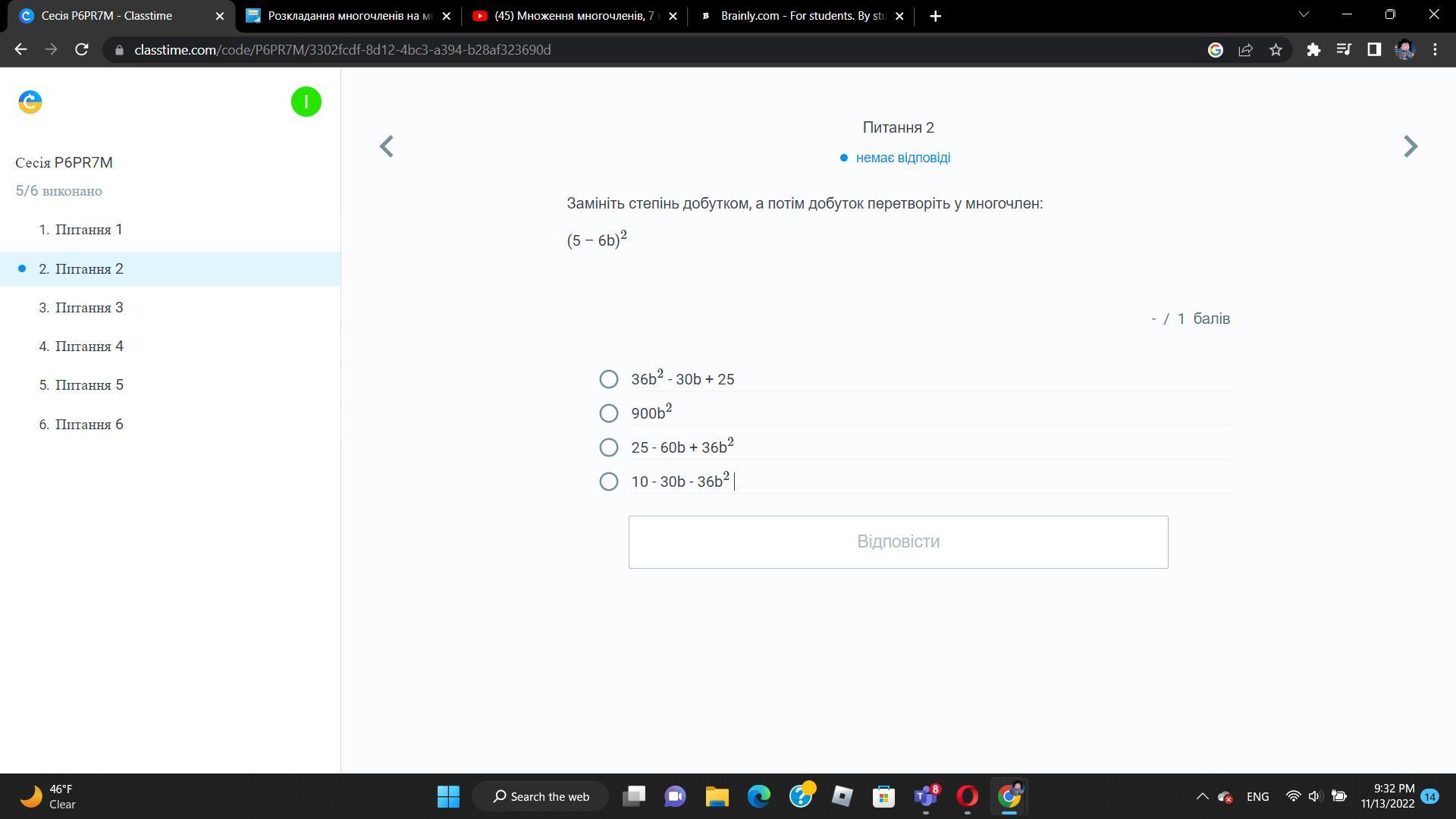
Answers
The value of (5 - 6b)² when it is expanded is 25 -60b + 36b² (third option).
What is the equivalent value?The square of a number is the value derived when a number is multiplied by itself. Multiplication is the mathematical operation that is used to determine the product of two or more numbers. The sign that is used to represent multiplication is x.
The square of a number is denoted by the power 2. For example, the square of 2, 2² is 4 (2 x 2).
Thus, (5 - 6b)² is the same as (5 - 6b) x (5 - 6b).
When multiplied, the expression becomes:
(5 - 6b) x (5 - 6b)
When multiplied, the expression becomes: 25 - 30b - 30b + 36b²
Add similar terms together: 25 -60b + 36b²
To learn more about the square of a number, please check: https://brainly.com/question/28610159
#SPJ1
What are the two methods of division?
Answers
Depending on the level of difficulty, there are three different dividing methods. These include the bus stop approach, the chunking method, and the long division method. The chunking method is also known as division by repeated subtraction.
what is division?One of the four fundamental arithmetic operations, or the process by which two or more numbers are added together to create a new number, is division. Multiplication, addition, and subtraction make up the remaining operations.
The opposite of multiplication is division.
Depending on the level of difficulty, there are three different dividing methods. These include the bus stop approach, the chunking method, and the long division.
To know more about division visit:-
https://brainly.com/question/21416852
#SPJ4
Which number is an integer? -3_4 1_5 2 4 2/3
Answers
Answer: -3
Step-by-step explanation:
The set of integers is a set of numbers that includes all negative numbers, all positive numbers, and zero.
Examples of integers are -4, 7, 0, -17.
Note that 1/2 is not an integer, but rather a rational number.
So now that we know what integers are, we will answer our question.
Which number is an integer? -3, -4, 1, -5, 2, 4, 2/3
In fact, all of these are integers, except 2/3.
Hence, this is the answer.Factor the monomial.
a) 11m3
Answers
The factored expression is: \(11m^3 = 11 \times m \times m \times m\)
What are monomials?Monomials are expressions that have a single term
The monomial expression is given as:
11m^3
Factor out 11, from the expression.
So, we have:
\(11m^3 = 11 \times m^3\)
Factor out m from the expression
\(11m^3 = 11 \times m \times m^2\)
Factor out m from the expression
\(11m^3 = 11 \times m \times m \times m\)
Hence, the factored expression is:
\(11m^3 = 11 \times m \times m \times m\)
Read more about factorization at:
https://brainly.com/question/24380382
The monomial 11m³ can be factored as follows:
11m³ = 11 × m × m × m
What are monomial:A monomial is an expression that is the product of constants and an integer powers of y, like 3y². The combination of monomial makes a polynomial.
To factor a monomial means to express it as a product of two or more monomials. For example
4y³ = 2y² × 2yNotice the factored value will give the same thing as the monomial.
Therefore, let's factor 11m³ completely.
11m³ = 11 × m × m × mlearn more on factoring here:https://brainly.com/question/24484751
Answer the following questions. "Proof by Venn diagram" is not an acceptable approach. Remember that mathematics is a language, and it is necessary to use correct grammar and notation. 1. If A and B are ANY two sets, determine the truth-values of the following statements. If a statement is false, give specific examples of sets A and B that serve as a counter- example (3 pts each). a. (A\B) CA b. Ac (AUB)
Answers
In this question, we are asked to determine the truth-values of two statements involving sets A and B. For each statement, we need to determine if it is true or false. If it is false, we need to provide specific counterexamples by choosing appropriate sets A and B.
a. (A\B) ⊆ A
The statement (A\B) ⊆ A is true for any sets A and B. This is because the set difference (A\B) contains elements that are in A but not in B. Therefore, by definition, every element in (A\B) is also an element of A. There are no counterexamples to this statement.
b. A^c ⊆ (AUB)
The statement\(A^c\) ⊆ (AUB) is true for any sets A and B. This is because the complement of A, denoted as \(A^c\), contains all elements that are not in A.
On the other hand, the union of A and B, denoted as (AUB), contains all elements that are in A or in B or in both.
Since the complement of A contains all elements not in A, it includes all elements in B that are not in A as well.
Therefore, \(A^c\) ⊆ (AUB) holds true for any sets A and B. There are no counterexamples to this statement.
In conclusion, both statements are true for any sets A and B, and there are no counterexamples.
To learn more about sets visit:
brainly.com/question/30705181
#SPJ11
Each boldface number is the value of either a parameter or a statistic. In each case, state which it is. In an experiment to test the effectiveness of single -sex classrooms, girls assigned at random to a coeducational chemistry class gained an average of 12.2 points from a pretest to a posttest. Girls assigned randomly to a single-sex chemistry class taught by the same teacher gained 15.1 points.
Answers
We are comparing the average gain in test scores for two different groups of girls - those assigned to coeducational chemistry classes and those assigned to single-sex chemistry classes. Since these gains are calculated from the data obtained from these specific groups of girls, they represent statistics rather than parameters.
In the given scenario:
The boldface number "12.2" represents a statistic.
The boldface number "15.1" represents a statistic.
A statistic is a numerical value that summarizes a sample of data, while a parameter is a numerical value that summarizes a population.
In this case, we are comparing the average gain in test scores for two different groups of girls - those assigned to coeducational chemistry classes and those assigned to single-sex chemistry classes. Since these gains are calculated from the data obtained from these specific groups of girls, they represent statistics rather than parameters.
Learn more about average gain from
https://brainly.com/question/26215194
#SPJ11
Table I contains outputs of the function f(x)=b^xf(x)=b
x
f, left parenthesis, x, right parenthesis, equals, b, start superscript, x, end superscript for some xxx values, and Table II contains outputs of the function g(x)=\log_b(x)g(x)=log
b
(x)g, left parenthesis, x, right parenthesis, equals, log, start base, b, end base, left parenthesis, x, right parenthesis for some xxx values. In both functions, bbb is the same positive constant.
Answers
The tables are illustrations of logarithmic and exponential functions
The missing value in table I is 1.292The missing value in table II is 1.544How to determine the missing valuesThe functions are given as:
\(f(x) = b^x\) --- table I
\(g(x) = log_b(x)\) --- table II
The above equations mean that:
Tables I and II are inverse functions
On the table II (see attachment), we have:
\(g(8) = 1.292\)
This means that:
\(f(1.292) = 8\)
Also, On the table I, we have:
\(f(1.544) = 12\)
This means that:
\(g(12) = 1.544\)
So, the missing values for both tables are 1.292 and 1.544
Read more about logarithmic and exponential functions at:
https://brainly.com/question/8993571

Linda is saving money to buy a game. So far she has saved $15, which is three-fifths of the total cost of the game. How much does the game cost?
Answers
Answer:
$25
Step-by-step explanation:
We Know
She has saved $15, which is three-fifths of the total cost of the game
How much does the game cost?
$15 = 3/5
$5 = 1/5
We Take
5 x 5 = $25
So, the cost of the game is $25.
Question 1(Multiple Choice Worth 2 points) (Making Predictions MC) A college cafeteria is looking for a new dessert to offer its 4,000 students. The table shows the preference of 225 students. Ice Cream Candy Cake Pie Cookies 81 9 72 36 27 Which statement is the best prediction about the slices of pie the college will need? The college will have about 480 students who prefer pie. The college will have about 640 students who prefer pie. The college will have about 1,280 students who prefer pie. The college will have about 1,440 students who prefer pie.
Answers
Answer:
Step-by-step explanation:
To make a prediction about the slices of pie the college will need, we can use the proportion of students who prefer pie from the sample of 225 students to estimate the number of students out of the total 4,000.
Number of students surveyed: 225
Number of students who prefer pie: 36
To estimate the number of students who prefer pie out of the total 4,000 students, we can set up a proportion:
225 (surveyed students) is to 36 (students who prefer pie) as 4,000 (total students) is to x (unknown number of students who prefer pie).
225/36 = 4000/x
Cross-multiplying, we get:
225x = 36 * 4000
225x = 144,000
x = 144,000/225
x ≈ 640
Therefore, the best prediction is that the college will have about 640 students who prefer pie.
The correct answer is "The college will have about 640 students who prefer pie."
NEED HELP FAST!
If Mimstoon bought 24 kents, how many lirns did she buy?

Answers
Answer:
96
Step-by-step explanation:
im right
The double number line shows that in 2 22 minutes, Pogo the dog can fetch a frisbee 6 66 times. A double number line with 5 equally spaced tick marks. The line labeled Time, minutes, reads from left to right: 0, an unlabeled tick mark, 2, two unlabeled tick marks. The line labeled Fetches, reads from left to right: 0, an unlabeled tick mark, 6, two unlabeled tick marks. A double number line with 5 equally spaced tick marks. The line labeled Time, minutes, reads from left to right: 0, an unlabeled tick mark, 2, two unlabeled tick marks. The line labeled Fetches, reads from left to right: 0, an unlabeled tick mark, 6, two unlabeled tick marks. Based on the ratio shown in the double number line, how many times will Pogo fetch the frisbee in 4 44 minutes? times
Answers
Pogo will fetch the frisbee approximately 13.36 times in 4 44 minutes.
What is Algebraic expression ?
Algebraic expression can be defined as combination of variables and constants.
From the double number line, we can see that in 2 22 minutes, Pogo can fetch the frisbee 6 66 times. This means that the ratio of fetches to time is:
6 66 / 2 22
To find out how many times Pogo will fetch the frisbee in 4 44 minutes, we can use this ratio. Let's call the number of fetches in 4 44 minutes "x". We can set up a proportion:
6 66 / 2 22 = x / 4 44
To solve for x, we can cross-multiply:
(6 66) × (4 44) = (2 22) × x
2964 = 222x
Dividing both sides by 222, we get:
x = 13.36 (rounded to two decimal places)
Therefore, Pogo will fetch the frisbee approximately 13.36 times in 4 44 minutes.
To learn more about Algebraic expression from given link.
brainly.com/question/953809
#SPJ1