A prestigious university wants to make sure that exactly 1 of 20 students who apply to the school are accepted.The university also wants to make sure that the ration of boys to girls accepted is 9 to 11.Of 5600 boys and 6000 girls apply to the school, how many boys can be accepted this year?
a. $249.
b. $261.
c. $319.
d. $331.
Answers
The number of boys accepted this year from the given students ratio is equal to option b. 261.
Number of boys = 5600
Number of girls = 6000
Ratio of boys to girls = 9 to 11
Find the total number of students applying to the school.
The total number of students applying to the school is the sum of the number of boys and the number of girls,
Total number of students = Number of boys + Number of girls
⇒Total number of students = 5600 + 6000
⇒Total number of students = 11600
Determine the number of students to be accepted.
The university wants to accept exactly 1 out of 20 students who apply.
To find the number of students to be accepted, divide the total number of students by 20,
Number of students to be accepted = Total number of students / 20
⇒Number of students to be accepted = 11600 / 20
⇒Number of students to be accepted = 580
Determine the ratio of boys to girls for the accepted students.
The university wants the ratio of boys to girls to be 9:11.
Since the total number of students to be accepted is 580,
set up the following equation,
Number of boys / Number of girls = 9 / 11
Solve for the number of boys.
Let us assume the number of boys accepted is x.
Then the number of girls accepted is 580 - x.
Using the ratio equation, set up the following equation,
⇒ x / (580 - x) = 9 / 11
To solve this equation, we can cross-multiply,
⇒11x = 9(580 - x)
⇒11x = 5220 - 9x
⇒20x = 5220
⇒x = 5220 / 20
⇒x = 261
Therefore, the number of boys that can be accepted this year from the number of students is by option b. 261.
Learn more about students here
brainly.com/question/28248286
#SPJ4
Related Questions
what is another name for a chord that passes through the center of the circle? A) Diameter B) Circumference C) center D) radius
Answers
Answer:
A
Step-by-step explanation:
diameter
The another name for the chord that passes through the center of the circle is the diameter.
The correct option is (A).
What is a circle?A circle is a closed, two-dimensional object where every point in the plane is equally spaced from a central point.
As per the given data:
We have to find out the alternate name for a chord that passes through the center of a circle out of the given options.
Diameter:
It's a chord that passes through the center and touches the ends of the circumference of the circle.
Hence, this is correct.
Circumference:
It's the length of the boundary of a circle, hence this cannot be a chord.
This is incorrect.
Center:
It's a point and a chord is a line, hence this cannot be true.
Radius:
A radius is not a chord, as it does not touch the endpoints on the circumference of the circle.
The another name for the chord that passes through the center of the circle is the diameter.
Hence, The another name for the chord that passes through the center of the circle is the diameter.
To learn more about circle, click:
brainly.com/question/29142813
#SPJ5
Suppose that the population of deer in a state is 7,700 and is growing 3% cach year. Predict the population
after 5 years
Answers
Answer:
Future Value= 8,927
Step-by-step explanation:
Giving the following information:
Present Value (PV)= 7,700
Growth rate (g)= 3%
Number of periods (n)= 5 years
To calculate the future value (FV) of the population after 5 years, we need to use the following formula:
FV= PV*(1 + g)^n
FV= 7,700*(1.03^5)
FV= 8,927
If we invest $100,000 today in an account earning 7% per year,
how many years until we have $500,000? Round to two decimals.
Answers
It would take approximately 19.65 years for an investment of $100,000 at a 7% annual interest rate to grow to $500,000. Rounded to two decimal places, the answer is 19.65 years.
To determine the number of years it will take for an investment of $100,000 at a 7% annual interest rate to grow to $500,000, we can use the compound interest formula:
A = P(1 + r/n)^(nt)
Where:
A = the future value of the investment ($500,000)
P = the initial principal amount ($100,000)
r = the annual interest rate (7% or 0.07)
n = the number of times that interest is compounded per year (assuming annually, so n = 1)
t = the number of years
Plugging in the values we know, we get:
$500,000 = $100,000(1 + 0.07/1)^(1*t)
Dividing both sides of the equation by $100,000 and simplifying:
5 = (1.07)^t
To solve for t, we can take the logarithm of both sides:
log(5) = log[(1.07)^t]
Using logarithmic properties, we can bring down the exponent:
log(5) = t * log(1.07)
Finally, we can solve for t by dividing both sides by log(1.07):
t = log(5) / log(1.07)
Using a calculator, we find:
t ≈ 19.65
Therefore, it would take approximately 19.65 years for an investment of $100,000 at a 7% annual interest rate to grow to $500,000. Rounded to two decimal places, the answer is 19.65 years.
Learn more about investment from
https://brainly.com/question/24703884
#SPJ11
Use alpha = 0. 5. A) A dry goods store owner believes that the average monthly income of its customers is P20 000. Ninety randomly selected customers are then asked for their monthly income, and the mean is P21 500 with a standard deviation of P1 200. Do the data provide sufficient evidence to indicate that the mean monthly income of the customers in the store is P20 000?
Answers
Based on the given data, there is evidence to suggest that the mean monthly income of the customers in the store is higher than P20 000.
The null hypothesis is that the mean monthly income of the customers in the store is P20 000, while the alternative hypothesis is that the mean monthly income is not P20 000. With a significance level of alpha = 0.5, a two-tailed t-test will be used to determine if there is sufficient evidence to reject the null hypothesis.
Using a t-test calculator, the calculated t-value is 7.07, which exceeds the critical t-value of 1.645. This indicates that there is sufficient evidence to reject the null hypothesis and accept the alternative hypothesis that the mean monthly income of the customers in the store is not P20 000.
However, it is important to note that this conclusion is only based on a sample of 90 customers and may not necessarily represent the entire population of the store's customers. A larger sample size may be needed to increase the accuracy and reliability of the results.
Visit here to learn more about Null- Hypothesis:
brainly.com/question/4436370
#SPJ11
In which coordinate of the point which divides the join of 1/7 and 4/3 in the ratio 2 3?
Answers
The coordinates of the point dividing the join of given points will be equal to (1, 3).
If we need to find the coordinates of a point P(x, y) dividing the join of points (x₁, y₁) and (x₂, y₂) in the ratio m:n then the formula is expressed as
P(x, y) = [(mx₂ + nx₁/m + n), (my₂ + ny₁/m + n)]
We have the values as m:n = 2:3 and
(x₁, y₁) = (-1, 7) and (x₂, y₂) = (4, -3)
On using the above formula we get
P(x, y) = [2(4) + 3(-1)/2 + 3, 2(-3) + 3(7)/2 + 3]
P(x, y) = [(8 - 3)/5, (-6 + 21)/5]
P(x, y) = (1, 3) which is the required coordinate.
Learn more about Coordinates at:
brainly.com/question/12959377
#SPJ4
Complete Question:
Find the coordinates of the point which divides the join of (-1, 7) and (4, - 3) in the ratio 2 : 3.
Please help me understand this math problem! :D

Answers
Answer:
48 cm^2
Step-by-step explanation:
First find the area of each shape.
2 triangles- [bxh]x1/2
(4 times 3)(divided by 2) = 6, but there are 2 triangles so 6+6=12
Square- (l x w)
3 times 3 (You get the other three from the other side of the rectangle) =9
Left rectangle- (l x w)
3 times 4 = 12
Right rectangle- (l x w)
5 times 3 (You get the three from the side of the square) = 15
Total: 2 triangles Area + Square Area + Left rectangle Area+ Right rectangle Area = Surface Area
12 + 9 + 12 + 15 = 48 cm^2
Hope this helps!!
Find the values of x and y.

Answers
The value of x is 5.
The value of y is 40°.
What is a triangle?It is a two dimensional figure which has three sides and the sum of the three angles is equal to 180 degrees.
We have,
A composite figure that has three triangles.
Two equilateral triangles.
One isosceles triangle.
We see that,
Both equilateral triangles have the same sides and the same angles.
5x - 1 = 24
5x = 24 + 1
5x = 25
x = 5
We see that,
Let the opposite angle of 6y° = m
6y° + 60 + 60 + m = 360
6y + 120 = 360
6y = 360 - 120
6y = 240
y = 40°
Thus,
x = 5 and y = 40°
Learn more about triangles here:
https://brainly.com/question/25950519
#SPJ1
After purchasing fence for a 8 by 8 feet square pen for his dog, Craig decided to enlarge the size of the pen to make each side 4 feet longer. The rice of the fence is $6.50 per foot.
How many feet of additional fence should Craig purchase to build his enlarged fence?
Answers
Since each side of the pen is being increased by 4 feet, the total increase in perimeter would be 4 feet multiplied by 4 sides, which equals 16 feet.
To determine how many feet of additional fence Craig should purchase, we need to calculate the increase in the perimeter of the enlarged pen. Therefore, Craig should purchase an additional 16 feet of fence to build his enlarged fence.
The original size of the pen is an 8 by 8 feet square, which means each side measures 8 feet. The perimeter of the original pen is calculated by adding up the lengths of all four sides, so 8 + 8 + 8 + 8 = 32 feet.
To enlarge the pen, Craig decides to increase each side by 4 feet. After the enlargement, each side of the pen would measure 8 + 4 = 12 feet. The perimeter of the enlarged pen is calculated in the same way, by adding up the lengths of all four sides: 12 + 12 + 12 + 12 = 48 feet.
To find the additional fence Craig needs to purchase, we subtract the original perimeter from the enlarged perimeter: 48 feet - 32 feet = 16 feet. Therefore, Craig should purchase an additional 16 feet of fence to build his enlarged fence.
This calculation is based on the assumption that the pen remains a square shape after enlargement. If the shape of the enlarged pen differs from a square, the calculation would vary.
Learn more about perimeter here:
brainly.com/question/7486523
#SPJ11
Arteriosclerosis is a disease in which the openings in the arteries become narrow because
of fatty deposits on the artery wall. It is found that fat deposits are building up uniformly
on the wall of an artery whose cross section is a circle of radius 5 mm. What is the rate
of the cross-sectional area of the artery opening changing relative to the thickness of the
fat deposit when the thickness of deposit is 2mm?
Answers
In this question, it is required to calculate the rate of the cross-sectional area of the artery opening changing relative to the thickness of the fat deposit when the thickness of deposit is 2mm. We will use derivatives to solve this problem.
Here is the solution:Let's take, A be the cross-sectional area of the artery, r be the radius of the artery, and t be the thickness of the fat deposit. Therefore, the radius of the artery can be given as r = 5mm, and the thickness of the fat deposit is given as t = 2mm.The cross-sectional area of the artery A can be given as follows:A = π(r-t)²Now, differentiate both sides of the above equation with respect to t.
dA/dt = d/dt (π(r-t)²) = 2π(r-t)(-1) Therefore, dA/dt = -2π(r-t)After substituting the values, we have r = 5mm and t = 2mm.dA/dt = -2π(5-2) = -6πmm²/mmHence, the rate of the cross-sectional area of the artery opening changing relative to the thickness of the fat deposit when the thickness of deposit is 2 mm is -6π mm²/mm.
To know more about cross-sectional area visit :
https://brainly.com/question/4365303
#SPJ11
What is the range of f/x )= sin x the set of all real numbers?
Answers
On solving the provided question we can say that - The Range of the given function, f(x) = sin(x) , Range = \(-1 < y < 1\)
What is Range?Range: the discrepancy between the top and bottom numbers. To get the range, locate the greatest observed value of the variable and deduct the least observed value (the minimum). The data points between the two extremes of the distribution are not taken into consideration by the range; just these two values are considered. Between the lowest and greatest numbers, there is a range. Values at the extremes make up the range. The data set 4, 6, 10, 15, 18, for instance, has a range of 18-4 = 14, a maximum of 18, a minimum of 4, and a minimum of 4.
The Range of the given function, f(x) = sin(x)
\(-1 < y < 1\)
To know more about Range visit:
https://brainly.com/question/12789483
#SPJ4
help plz i will make a brainllest quick
plzzz

Answers
Answer:
a
Step-by-step explanation:
Answer:
the answer is a.
Step-by-step explanation:
I did this one.
4(-2x - 9) distrubutive property
Answers
Answer:
-8x-36 i think
Step-by-step explanation:
Answer: -8x-36
Step-by-step explanation: multiply -2x by 4 and -9 by 4
Select the correct answer. Simplify the expression.
(see the screenshot)
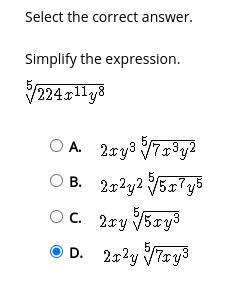
Answers
Answer:
Option D
Step-by-step explanation:
Given expression has been given as,
\(\sqrt[5]{224x^{11}y^8}\)
\(\sqrt[5]{224x^{11}y^8}=\sqrt[5]{2\times 2\times 2\times 2\times 2\times 7(x^{11})(y^8)}\)
\(=\sqrt[5]{(2^5)\times (7)(x^{10}\times x)(y^5\times y^3)}\)
\(=2^{\frac{5}{5}}\times 7^{\frac{1}{5}}\times x^{\frac{10}{5}}\times x^{\frac{1}{5}}\times y^{\frac{5}{5} }\times y^{\frac{3}{5} }\)
\(=2\times 7^{\frac{1}{5}}\times x^2\times y\times x^{\frac{1}{5} }\times y^{\frac{3}{5} }\)
\(=2x^2y\sqrt[5]{7xy^3}\)
Option D will be the answer.
Q1) (15 pts) a) Find the complementary (homogeneous) solution of y(5) — y(3) = f(t). b) Determine the particular solution yp (t) if (i) f(t) = et (ii) f(t) = 2t² (iii) f(t) = (3t+2) Cos2t Using the method of undetermined coefficients (Do not calculate the coefficients). (Other methods will not be graded.) 2) (10 pts) Find a linear differential equation whose general solutions is y(x) = C₁e* + C₂xe* + C3e *Cos 2x + C4e-*Sin 2x
Answers
1a) Complementary solution: y(t) = c₁ + c₂e^t + c₃e^(-t) + c₄cos(t) + c₅sin(t)
1b) Particular solutions:
(i) yp(t) = (1/2)e^t
(ii) yp(t) = (1/5)t^2 + (2/15)
(iii) yp(t) = [(3/20)t^2 + (1/4)t + C₁]cos(2t) - [(3/40)t^3 + (1/8)t^2 + C₂]sin(2t)
2) Linear differential equation: y''(x) + 4y'(x) + 5y(x) = 0
1a) To find the complementary solution of y(5) - y(3) = f(t), we need to find the homogeneous solution of the differential equation y(5) - y(3) = 0. We assume that y(t) = e^(rt) and substitute it into the differential equation to obtain the characteristic equation:
r^5 - r^3 = 0
r = 0, ±1
Since there are three distinct roots, the complementary solution is of the form:
y(t) = c₁ + c₂e^t + c₃e^(-t) + c₄cos(t) + c₅sin(t)
where c₁, c₂, c₃, c₄, and c₅ are constants.
1b) Using the method of undetermined coefficients, we can determine the particular solution of y(5) - y(3) = f(t) for each of the given functions f(t):
(i) f(t) = e^t
Assuming yp(t) = Ae^t, we obtain:
A(e^(5t) - e^(3t)) = e^t
A = 1/2
yp(t) = (1/2)e^t
(ii) f(t) = 2t^2
2A(t^5 - t^3) + 6B(t^3 - t) + 6C(t^2 - 1) = 2t^2
A = 1/5, B = 0, C = 2/15
yp(t) = (1/5)t^2 + (2/15)
(iii) f(t) = (3t+2)cos(2t)
A''(t)cos(2t) + B''(t)sin(2t) + 4A'(t)sin(2t) - 4B'(t)cos(2t) = (3t+2)cos(2t)
A(t) = (3/20)t^2 + (1/4)t + C₁
B(t) = -(3/40)t^3 + (1/8)t^2 + C₂
yp(t) = [(3/20)t^2 + (1/4)t + C₁]cos(2t) - [(3/40)t^3 + (1/8)t^2 + C₂]sin(2t)
2) The given general solution is:
y(x) = C₁e^x + C₂xe^x + C₃e^(-x)cos(2x) + C₄e^(-x)sin(2x)
y'(x) = C₁e^x + C₂(e^x + xe^x) - C₃e^(-x)sin(2x) + C₄e^(-x)cos(2x)
y''(x) = C₁e^x + C₂(2e^x + xe^x) + C₃e^(-x)cos(2x) - C₄e^(-x)sin(2x)
(C₁ + C₂ + C₃ + C₄)e^x + (2C₂ + C₂x - C₃sin(2x) + C₄cos(2x))e^x + (-C₁ + 2C₂ - C₃cos(2x) - C₄sin(2x))e^(-x) = 0
Since this equation must hold for all values of x, we obtain the following system of equations:
C₁ + C₂ + C₃ + C₄ = 0
2C₂ - C₁ - C₃cos(2x) - C₄sin(2x) = 0
C₂x - C
To know more about linear differential equation, visit:
brainly.com/question/30323408
#SPJ11
Please help me on this question....

Answers
Answer:
vvvgghhi
hi
Step-by-step explanation:
ggguuuuuuuuhh
URGENT!!! ITS DUE IN 5 MINUTES!!!!

Answers
Answer:
d
Step-by-step explanation:
I'll edit my response to tell you why later. it seems like you need this answer now.
Answer:
A?
Step-by-step explanation:
I'm pretty sure thats the answer! I,m currently learning that in class so I might be wrong!
PLS ANSWER! MY ASSIGNMENT IS OVERDUE!!! I know that the answer is 3, but I don't know how to get it.

Answers
Answer:
multiply 6x10then by 20
In the expression 73 – 4•3+8, the first operation is...? A.an exponent
B.subtraction.
C.multiplication.
D.addition.
Answers
Answer:
C. multiplication
Step-by-step explanation:
P= ()
E=^
M=x
D=/
A=+
S=-
Find the values of x and y

Answers
Answer:
well, y=8 and x=50
Step-by-step explanation:
you actually have the angle 128 wrong, and it is suppose to be 32 degrees, which changes it up and all you have to do to find y because angle 32 and 4y are vertical, is divide 32/4=y which is 8, for x, it is vertical to 148 making those even, and it would be as simple as reversing the equation so, 148+2=150, and ddivided by 3 is 50 degrees
Answer:
x=50
y=8
Step-by-step explanation:
3x-2 and 148 are vertical angles and vertical angles are equal
3x-2 =148
Add 2 to each side
3x-2+2 =148+2
3x= 150
Divide by 3
3x/3 =150/2
x = 50
148 and the empty angle form a straight line so they add to 180
180-148 = 32
The empty angle is 32
4y and 32 are vertical angles so they are the same
4y = 32
4y/4 = 32/4
y = 8
Hey there! Can anyone help me out with this? I need help with both of these. Will give brainliest! :D

Answers
\(area = length \times width\)
____________________________________________
c .
\(area = \frac{3}{8} \times \frac{4}{5} \\ \)
\(area = \frac{4 \times 3}{4 \times 2 \times 5} \\ \)
\(area = \frac{3}{2 \times 5} \\ \)
\(area = \frac{3}{10} \: \: {cm}^{2} \\ \)
_____________________________________________
d.
\(area = \frac{1}{4} \times \frac{3}{7} \\ \)
\(area = \frac{3}{28} \: \: {m}^{2} \\ \)
What is the value of y when x = 6?
-3x + 9y = 18
Answers
Answer:
y = 6
Step-by-step explanation:
-3x + 9y = 18
-3(6) +6y = 18
-18 +6y = 18
Add 18 to each side
-18+18 +6y =18+18
6y = 36
Divide each side by 6
6y/6 = 36/6
y = 6
Angle B= 27, a=28ft, b=18ft solve for measurement(s) of angle c
Answers
Answer: In a triangle, the sum of the angles is 180 degrees. Therefore, if we know two of the angles, we can use this property to find the measure of the third angle.
In this case, we are given angle B = 27 degrees and we want to find the measure of angle C. We can use the following equation to find angle C:
Angle B + Angle C + Angle A = 180
27 + Angle C + 90 = 180
Angle C = 180 - 27 - 90
Angle C = 63 degrees
Additionally, we can use the Law of Cosines to find the measure of angle C.
c² = a² + b² - 2ab * cos(C)
c² = 28² + 18² - 2 * 28 * 18 * cos(C)
c² = 784 + 324 - 1008 * cos(C)
c = √(1108 - 1008*cos(C))
We know that cos(C) = (a² + b² - c²) / 2ab
cos(C) = (784 + 324 - c²) / (22818)
We can substitute the value of c² that we obtained from the first equation and find cos(C) and thus angle C.
So the measure of angle C is 63 degrees.
Step-by-step explanation:
A Bunch of Systems
Solve each system of equations without graphing and show your reasoning. Then, check
your solutions.
2x + 3y = 7
-2x + 4y = 14
Answers
Answer:
(- 1, 3 )
Step-by-step explanation:
2x + 3y = 7 → (1)
- 2x + 4y = 14 → (2)
add (1) and (2) term by term to eliminate x
(2x - 2x) + (3y + 4y) = (7 + 14)
0 + 7y = 21
7y = 21 ( divide both sides by 7 )
y = 3
substitute y = 3 into either of the 2 equations and solve for x
substituting into (1)
2x + 3(3) = 7
2x + 9 = 7 ( subtract 9 from both sides )
2x = - 2 ( divide both sides by 2 )
x = - 1
As a check
substitute the values of x and y into the left side of both equations and if equal to the right side in both equations then the values of x and y are true.
(1) 2(- 1) + 3(3) = - 2 + 9 = 7 ← true
(2) - 2(- 1) + 4(3) = 2 + 12 = 14 ← true
then (- 1, 3 ) is the solution to the system
Answer:(- 1, 3 )
Step-by-step explanation:
Yesterday was the first day of the Dodge County Fair. The fair's organizers estimated 1,200 people would attend. Unfortunately, it rained, so only 960 people attended. What is the percent error for the organizers' estimate?
Answers
The percent error for the organizers estimate of people who would attend as required is; 20%.
What is the percent error for the organizers estimate of people who would attend?It follows from the task content that the percent error for the organizers estimate is to be determined as required.
As evident in the task content; the organizers estimate is; 1200 while only 960 people actually attended.
Therefore, the error associated which the estimation when expressed as a percentage is;
percent error = { ( 1200 - 960 ) / 1200 } × 100%
Percent error = ( 240 / 1200 ) × 100%
Percent error = 0.2 × 100%
= 20%.
On this note, the required percent error is; 20%.
Read more on percent error;
https://brainly.com/question/29810631
#SPJ1
Answer:
ITS 25%
Step-by-step explanation:
To find the percent error, start by listing the key information from the problem.The fair's organizers estimated 1,200 people would attend the first day of the fair.960 people actually attended.First, find the amount of error. It is the difference between 1,200 and 960, which is 240.Now, use the formula to find the percent error.percent error=amount of errorcorrect amount=240960=0.25You can rewrite 0.25 as 25%. So, the percent error of the organizers' estimate is 25%IXL
ahshepfnshaudjfornds
(word count lol)

Answers
Answer:
455666
124
Step-by-step explanation:
Someone please help me
The top number is 18

Answers
Answer:
x = 24
Step-by-step explanation:
Since this is a right angle, we can use the Pythagorean Theorem to find x. In the formula, a^2 + b^2 = c^2, variables a and b represent the lengths of the legs, and variable c represents the length of the hypotenuse.
a^2 + b^2 = c^2
18^2 + x^2 = 30^2
324 + x^2 = 900
x^2 = 576
x = 24
In circle SS, ST=5ST=5 and m\angle TSU=50^\circ∠TSU=50∘ Find the length of \overset{\LARGE\frown}{TU} TU⌢ . Express your answer as a fraction times \piπ.

Answers
The length of arc TU, as a fraction terms of π, is calculated as: 25/18 π units.
How to Find the Length of an Arc of a Circle?The length of an arc of a circle is the distance around the portion of the circumference of a circle that is marked by two points connected to the radius of the circle. Given r as the radius length and ∅ is the central angle measure, the length of the arc of the circle can be calculated as:
Arc length = ∅/360 × 2 × π × r.
Given the following:
Central angle (∅) = m∠TSU = 50°
Radius of the circle (r) = 5
Plug the values into ∅/360 × 2 × π × r:
Arc length = 50/360 × 2 × π × 5
Arc length = (50 × 2 × π × 5)/360
Arc length = 500/360 × π
Arc length = 50/36 × π
Arc length = 25/18 × π
Arc length of TU = 25/18 π units
Thus, the length of arc TU, as a fraction terms of π, is calculated as: 25/18 π units.
Learn more about the length of arc on:
https://brainly.com/question/2005046
#SPJ1
Evaluate the expression: 2x + 5 for x = 3
Answers
Substitute the value of the variable into the equation and simplify.
11
11
A yearly subscription to a monthly magazine costs £42.00. How much does each issue
cost?
Answers
Each issue will cost £3.5 if a yearly subscription to a monthly magazine costs £42.00.
Given, a yearly subscription to a monthly magazine costs £42.00 i.e., 12 months to a monthly magazine costs £42.00.
one month will cost £42.00 divide by 12 and let it be x.
we simply calculate the value of x by dividing £42.00 by 12.
x = 42.00/12
x = 3.5
x = £3.5
Therefore, each issue will cost £3.5 if a yearly subscription to a monthly magazine costs £42.00.
Learn more in depth about linear equation at https://brainly.com/question/25109150
#SPJ9
vector right ray(a) has a magnitude 5.00 and points in a direction 50.0° counterclockwise from the positive x axis. what are the x and y components of vector right ray(a).
Answers
To find the x and y components of the vector, we can use trigonometry. The x component can be determined by multiplying the magnitude by the cosine of the angle, and the y component can be obtained by multiplying the magnitude by the sine of the angle.
To determine the x and y components of the vector "right ray(a)," we use trigonometry. The magnitude of the vector is given as 5.00, and the direction is specified as 50.0° counterclockwise from the positive x-axis.
The x component can be found by multiplying the magnitude by the cosine of the angle. In this case, it would be x = 5.00 * cos(50.0°).
Similarly, the y component can be determined by multiplying the magnitude by the sine of the angle. Therefore, the y component is y = 5.00 * sin(50.0°).
By calculating these trigonometric functions, we can find the values for the x and y components of the vector "right ray(a)." These components represent the horizontal and vertical displacements of the vector in the Cartesian coordinate system.
To learn more about vector components click here: brainly.com/question/17016695
#SPJ11